Tasks - AtCoder Regular Contest 149

又是114514年前做的題，現在來寫

屯了好多，清一下庫存

A - Repdigit Number (atcoder.jp)

直接暴力列舉所有每一位都為\(x\)的數，然後數位從\(1\)到\(n\)，若當前列舉到了\(i\)，設\(i-1\%M\)為\(now\)，則\(now=(now*10+x)\%M\)，若\(now\)為\(0\)，則\(++cnt\)

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5;
int n,m,t;
bool vis[10];
int num,sz;
signed main(){
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=9;++i){
		int sur=0;
		for(int j=1;j<=n;++j){
			sur=(sur*10+i)%m;
			if(!sur){
				if(j==sz) num=max(num,i);
				if(j>sz) sz=j,num=i;
			}
		}
	}
	if(!sz) printf("-1");
	for(int i=1;i<=sz;++i) printf("%lld",num);
	
	return 0;
}

B - Two LIS Sum (atcoder.jp)

因為\(A_i\)與\(B_i\)是繫結的，所以可以畫成幾個牌子並且一個牌子分上下兩個部分，上半部分為\(A_i\)，下半部分為\(B_i\)

因為並沒有對運算元目做出限制，所以這個操作實際上就是對\(n\)塊牌子隨便排序，求\(MAX\{LIS(A)+LIS(B)\}\)

我們可以將\(LIS(A)\)所使用的\(A_i\)和\(LIS(B)\)所使用的\(B_i\)染色，然後就是下圖的樣子

然後我們可以發現，答案最優時，一定是\(\forall i\)，\(A_i\)被染色

一塊牌子如果沒有染色，如果我們想讓它的\(A_i\)染上顏色，那麼我們可以將這塊牌子放到\(A_i\)有染色的牌子\(j\)和\(k\)之間（\(j<k\)，且滿足\(j\)和\(k\)之間\(\nexists l\)，\(A_l\)有染色、\(A_j<A_i<A_k\)），因為\(A\)和\(B\)的值都是全排列，所以如果不存在這樣的\(j\)和\(k\)，當且僅當\(A_i=1/n\)，那麼直接將這塊牌子放到末尾即可

又因為這塊牌子原先沒有染色，現在\(A_i\)染了色，且\(B_i\)有可能染色，而且其它牌子的染色情況沒有發生變化，所以答案最優時，一定是\(\forall i\)，\(A_i\)被染色

如果一塊牌子原先\(B_i\)有染色，\(A_i\)沒有染色，那麼還是像\(1.\)一樣操作。此時，\(A_i\)被染色，\(B_i\)可能失去染色，也有可能沒有，總之整體的染色數量只可能不變或\(+1\)，也就是不會虧

所以我們直接將牌子按照\(A\)從小到大排序，因為\(A\)和\(B\)都是全排列，所以現在\(B\)的順序是固定的，又根據上述證明，直接算出當前\(B\)的\(LIS\)即可

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int n,ans;
struct node{
	int a,b;
	bool operator < (const node&other) const{
		return a<other.a;
	}
}cn[N];
int c[N];
void add(int x,int y){
	for(;x<=n;x+=x&-x) c[x]=max(c[x],y);
}
int ask(int x){
	int ans=0;
	for(;x;x-=x&-x) ans=max(ans,c[x]);
	return ans;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i) scanf("%d",&cn[i].a);
	for(int i=1;i<=n;++i) scanf("%d",&cn[i].b);
	sort(cn+1,cn+n+1),ans=n;
	for(int i=1,f;i<=n;++i)
		f=ask(cn[i].b)+1,add(cn[i].b,f);
	printf("%d",ans+ask(n));


	return 0;
}

C - Avoid Prime Sum (atcoder.jp)

因為要求相鄰的數相加不是質數，而我們知道，偶數中只有\(2\)是質數且\(2\)不能通過從\([1,+\infty)\)中選兩個不同的數相加得到，也就是說，我們可以直接在矩陣的上半部分放奇數，下半部分放偶數

那麼對於奇數和偶數相鄰的部分，

當\(N\%2==0\)時

此時奇數在上面，偶數在下面，而\(奇數*2=偶數\)，所以我們在這一排奇數放\(i\in[3,2(N+1)+1](i\%2=1)\)，偶數這一排就對應放\(i*2\)，他們加起來就是\(3*i\)，不是質數

這樣放的話只有\(N=4\)的時候會存在放的偶數\(>N*N\)的情況，所以\(4\)直接特判

當\(N\%2==1\)時

我們可以發現，這個情況下的奇數和偶數相鄰的位置和\(N\%2==0\)的情況類似，只不過會多一個轉折，也就是說有一個奇數會和兩個偶數相鄰

所以我們可以直接找到兩個特殊的奇數和兩個特殊的偶數，使得將這兩個奇數放在轉折處，這兩個偶數放在這個兩個奇數下方可以使得題目的要求成立

經過一番尋找，可以發現有一種方案如圖

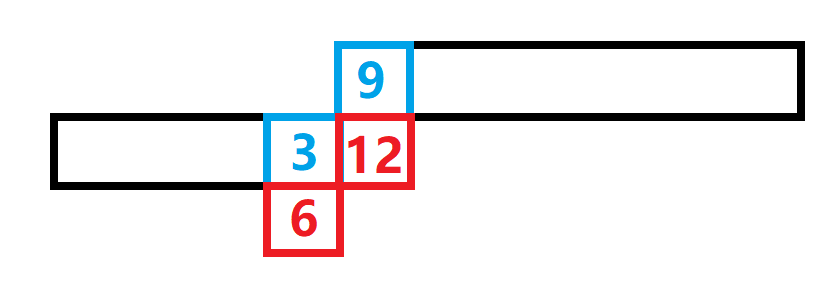
其它位置按照\(N\%2==0\)的方案放即可

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5;
int n,ans[N][N],now;
bool flag[N*N];
void pt(int x){
	printf("%d ",x);
	if(++now==n) now=0,printf("\n");
}
int main(){
	scanf("%d",&n);
	if(n==3) return printf("3 5 1\n9 7 8\n6 2 4"),0;
	if(n==4) return printf("15 11 16 12\n13 3 6 9\n14 7 8 1\n4 2 10 5"),0;
	if(n&1){
		pt(1);
		for(int i=(n<<1)+3;i<=n*n;i+=2) pt(i);
		pt(9);
		for(int i=5;i<=(n<<1)+1;i+=2) if(i!=9) pt(i);
		pt(3),pt(12),flag[12]=true;
		for(int i=5;i<=(n<<1)+1;i+=2) if(i!=9) pt(i<<1),flag[i<<1]=true;
		pt(6),flag[6]=true;
		for(int i=2;i<=n*n;i+=2){
			if(flag[i]) continue; 
			pt(i);
		}
	}else{
		pt(1);
		for(int i=n+2;i<=n*n/2;++i) pt((i<<1)-1);
		for(int i=2;i<=n+1;++i) pt((i<<1)-1);
		for(int i=2;i<=n+1;++i) pt((i<<1)-1<<1),flag[(i<<1)-1<<1]=true; 
		for(int i=2;i<=n*n;i+=2){
			if(flag[i]) continue;
			pt(i);
		}
	}


	return 0;
}

D - Simultaneous Sugoroku (atcoder.jp)

考慮如果\(X\)為\([1,10^6]\)的全排列，那麼我們就可以把\(X\)搬到數軸上去

在某一時刻\(T\)，可以發現對於\(X_i=-X_j\)，\(i\)和\(j\)的\(X\)值在接下來的任何時刻都是相反數，這給了我們啟發

因為\(X\)時全排列，也就是說在\(X\)第一次觸碰到負半軸時，整個\(X\)序列一定是跨過原點的連續的一段，這時，我們可以直接將數位數量較少的半軸上的數位\(A_i\)的\(i\)掛到另一個半軸上的數位\(A_j=-A_i\)的\(j\)上，最後輸出答案的時候直接將\(j\)的答案取相反數，就是\(i\)的答案

#include<bits/stdc++.h>
#define pii pair<int,int>
#define mp make_pair
#define fi first
#define se second
#define pb push_back
using namespace std;
const int N=3e5+5,MAXN=1e6;
int n,m,x[N],d[N],fa[MAXN+5];
vector<int> edge[MAXN+5];
pii ans[MAXN+5];
void dfs(int x,int depth,int f,int s){
	ans[x]=mp(f,s*(depth?-1:1));
	for(auto y:edge[x]) dfs(y,depth^1,f,s);
}
int main(){
	memset(ans,-1,sizeof(ans));
	for(int i=1;i<=MAXN;++i) fa[i]=i;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i) scanf("%d",&x[i]); 
	for(int i=1;i<=m;++i) scanf("%d",&d[i]);
	int l=1,r=MAXN,zero,change=0;
	for(int i=1;i<=m;++i){
		if(l>r) break;
		if(l+change>0) change-=d[i];
		else change+=d[i];
		zero=-change;
		if(zero<l||zero>r) continue;
		ans[zero]=mp(1,i);
		if(zero-l>=r-zero){
			for(int i=zero+1;i<=r;++i) fa[i]=zero*2-i,edge[zero*2-i].pb(i);
			r=zero-1;
		}else{
			for(int i=l;i<zero;++i) fa[i]=zero*2-i,edge[zero*2-i].pb(i);
			l=zero+1;
		}
	}
	for(int i=l;i<=r;++i) ans[i]=mp(0,i+change);
	for(int i=1;i<=MAXN;++i) if(fa[i]==i) dfs(i,0,ans[i].fi,ans[i].se);
	for(int i=1;i<=n;++i){
		if(ans[x[i]].fi) printf("Yes %d\n",abs(ans[x[i]].se));
		else printf("No %d\n",ans[x[i]].se);
	}
	return 0;
}

E - Sliding Window Sort (atcoder.jp)

將題目的操作改為有一個大小為\(M-1\)的序列\(S\)，其中的元素按從小到大的順序排列，還有一個大小為\(N-M+1\)的佇列\(T\)，每次把\(T\)的隊首放到\(S\)裡去，再把\(S\)的隊首放到\(T\)的隊尾

然後題目一下就簡單起來了，因為我們可以把任何次數操作都轉換成\(N-M+1\)次操作

當\(k=N-M+1\)時，最後的答案，也就是題目輸入的\(B\)，就是把\(S\)接到\(T\)的後面即可

當\(k=N-M+2\)時，\(B_{N-M+2}\)就是將\(B_{N-M+1}\)中\(T\)向前轉一個，再將整個\(B_{N-M+1}\)向後轉一個

總結一下，大概就是

當\(k<N-M+1\)時，只需要把\(i\in[k+M,N]\)的\(B_i\)(題目中給出的序列)直接甩掉，將\(N\)改成\(k+M-1\)即可

當\(k>N-M+1\)時，\(S\)已經固定了，而\(T\)就是在不斷的迴圈移動，所以可以直接還原到\(k=N-M+1\)時的序列

那麼現在我們已經使得\(k=N-M+1\)，如果當前情況下\(S\)不為\([N-M+2,N]\)的全排列，則無解；否則，對於\(S\)中的數位，選出它們的方案數為\((M-1)!\)

對於還原後到\(k=N-M+1\)狀態下的\(T\)，如果\(T_i>T_{i+1}\)，說明\(T_{i+1}\)是在選出\(T_i\)後再加入\(S\)並且在選\(T_{i+1}\)時被選出，也就是說\(T_{i+1}\)在放入的一瞬間就被拿出來了，換句話說，\(T_{i+1}\)的位置是唯一確定的；所以我們要求還原後的\(T\)為單調上升的，求出這個單調上升的長度，設初始時\(S\)為\(X\)，\(T\)為\(Y\)，對於每個\(T_i\)，有可能是從\(X\)或\(Y_{[1,i]}\)中取出來的，而選\(T_i\)的時候，已經確定了\(j\in[1,i-1]\)的位置且對於\(k\in(i,N]\)的位置，要麼沒確定，要麼已經固定在了\(Y_k\)，所以\(T_i\)可以選的位置的數量為\(M-1+i-(i-1)=M\)

答案就是\((M-1)!*M^{單調上升的長度}\)