Support Vector Machines

Perceptron and Linear Separability

假設存在一個 linear decision boundary，它可以完美地對 training dataset 進行分割。那麼，經由上述 Perceptron Algorithm 計算，它將返回哪一條 linear separator？

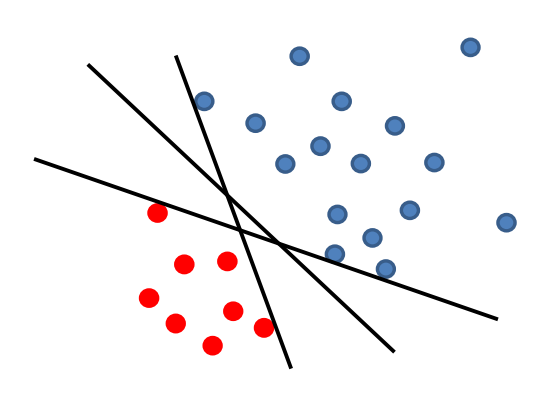
當 linear separator（即一個給定的超平面）的 margin \(\gamma\) 越大，則該模型的歸納與概括的效能越強。從幾何的角度（二維）的角度來理解非常直觀，我們需要這麼一條 linear separator，即，它既能對 training dataset 進行完美的分割，同時，我們希望距它最近的資料點距它的距離最大化（如上圖中間的那根直線）。否則，如果存在一個資料點距該 linear separator 的距離不是那麼遠，從直覺來說，圍繞在該資料點附近且與它 label 相同的一個新資料點隨意體現出的一個隨機波動，將使得這個新資料點越過 linear separator，導致分類錯誤。

因此，現在的問題是，如何將 margin 納入考量以求得這條最佳的 linear boundary？支援向量機將很好地解決這個問題。

Motivation（Why SVM？）

以下是 SVM 體現出的眼見的優勢：

SVM 返回一個 linear classifier，並且由於其演演算法使 margin solution 最大化，故這個 linear classifier 是一個穩定的解。
對 SVM 稍加改變，則能提供一種解決當資料集 non-separable 情況的方法。
SVM 同樣給出了進行非線性分類的隱性方法（implicit method，即上述的 kernel transformation）。

SVM Formula

假設存在一些 margin \(\gamma \in \Gamma\) 使得 training dataset \(\mathcal{S} = \mathcal{X} \times \mathcal{Y}\) 線性可分（但注意 linear separator 不一定穿過空間的原點）。

那麼，decision boundary：

\[g(\vec{x}) = \vec{w} \cdot \vec{x} - b = 0 \]

Linear classifier：

\[\begin{align*} f(\vec{x}) & = \text{sign}\big( g(\vec{x}) \big) \\ & = \text{sign} \big( \vec{w} \cdot \vec{x} - b \big) \end{align*} \]

思路

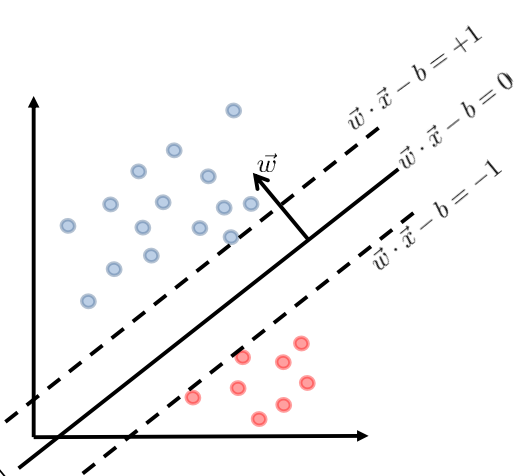
我們先分別求兩個平行的超平面，使得它們對所有的 training data point 進行正確的分類，再使這兩個超平面之間的距離最大化。

這也是所謂「支援向量機（Support Vector Machine）」名稱的由來，我們最終選定的支援向量 \(\vec{w}\) 就像千斤頂一樣將上述兩個平行的超平面「支撐」開來，並且支撐開的距離也將是儘可能的最大，如下圖所示。

Derivation

如上圖，兩個超平面的 decision boundary 可以寫作：

\[\begin{cases} \vec{w} \cdot \vec{x} - b = 1 \\ \vec{w} \cdot \vec{x} - b = -1 \end{cases} \]

則兩個超平面之間的距離為：

\[\frac{2}{||\vec{w}||} \]

對於初學者的直觀理解，推導可以通過二維平面上點到直線的距離進行類比，已知點 \((x_{0}, y_{0})\) 到直線 \(Ax + By + C = 0\) 的計算公式為：

\[\frac{|Ax_{0} + By_{0} + C|}{\sqrt{A^{2} + B^{2}}} \]

因此，設 \(\vec{w} \cdot \vec{x} - b = 1\) 上任意一點的座標為 \(\vec{x_{0}}\)，故滿足：

\[\vec{w} \cdot \vec{x_{0}} - b - 1 = 0 \]

那麼兩平行超平面之間的距離為該點到另一超平面 \(\vec{w} \cdot \vec{x} - b = -1\) 的距離，即：

\[\begin{align*} \frac{|\vec{w} \cdot \vec{x_{0}} - b + 1|}{\sqrt{||\vec{w}||^{2}}} & = \frac{|\big( \vec{w} \cdot \vec{x_{0}} - b - 1 \big) + 2|}{\sqrt{||\vec{w}||^{2}}} \\ & = \frac{2}{||\vec{w}||} \end{align*} \]

因此，對於 \(\forall i \in \mathbb{N}^{+}\)，當：

\[\begin{cases} \vec{w} \cdot \vec{x_{i}} - b \geq 1 \qquad \qquad \text{if } y_{i} = 1 \\ \vec{w} \cdot \vec{x_{i}} - b \leq -1 \qquad \quad \ \text{if } y_{i} = -1 \end{cases} \]

則 training data 全部被正確地分類。

理解

參考上圖，此處 \(\vec{w} \cdot \vec{x_{i}} - b \geq 1\) 和 \(\vec{w} \cdot \vec{x_{i}} - b \leq -1\) 的幾何意義是，將對於 label 為 \(1\) 和 \(-1\) 的 data point 分別排除在超平面 \(\vec{w} \cdot \vec{x} - b = 1\) 和 \(\vec{w} \cdot \vec{x} - b = -1\) 的兩邊外側，從而留下兩個超平面之間的空檔。

我們合併上面兩式為一個式子，則 training data 全部被正確地分類等價於：

\[\forall i \in \mathbb{N}^{+}: ~ y_{i} \big( \vec{w} \cdot \vec{x_{i}} - b \big) \geq 1 \]

現在我們得到了兩個超平面的距離表示式 \(\frac{2}{||\vec{w}||}\)，同時需要滿足 constraints \(y_{i} \big( \vec{w} \cdot \vec{x_{i}} - b \big) \geq 1\) for \(\forall i \in \mathbb{N}^{+}\)，我們希望在約束條件下使 \(\frac{2}{||\vec{w}||}\) 最大，那麼 SVM 轉變為運籌問題的求解，i.e.，

\[\begin{align*} \text{maximize: } \quad & \frac{2}{||\vec{w}||} \\ \text{subject to: } \quad & y_{i} \big( \vec{w} \cdot \vec{x_{i}} - b \big) \geq 1, \quad \forall i \in \mathbb{N}^{+} \end{align*} \]

SVM Standard (Primal) Form

注意到，\(||\vec{w}|| \geq 0\) 恆成立，且若 \(||\vec{w}|| = 0\) 時，支援向量（即權重向量）\(\vec{w}\) 為零向量，使得 linear separator 無意義。故最大化 \(\frac{2}{||\vec{w}||}\) 等價於最小化 \(\frac{1}{2} ||\vec{w}||\)。類似於線性迴歸中使用 Mean Square Error 而非 Mean Absolute Error 作為 loss function 的原因，\(||\vec{w}||\) 在原點處不可微，因此我們選擇 minimize \(\frac{1}{2} ||\vec{w}||^{2}\)，而非原形式 \(\frac{1}{2}||\vec{w}||\)，這當然是等價的。

故 SVM Standard (Primal) Form 如下：

\[\begin{align*} \text{minimize: } \quad & \frac{1}{2} ||\vec{w}||^{2} \\ \text{subject to: } \quad & y_{i} \big( \vec{w} \cdot \vec{x_{i}} - b \big) \geq 1, \quad \forall i \in \mathbb{N}^{+} \end{align*} \]

SVM When Training Dataset is Non-separable

當 training dataset 無法被全部正確地分類時（即，不存在一個 margin \(\gamma \in \Gamma\) 使得 training dataset \(\mathcal{S} = \mathcal{X} \times \mathcal{Y}\) 線性可分），可以引入 slack variables 求解問題。

SVM Standard (Primal) Form with Slack

SVM Standard (Primal) Form with Slack 如下所示：

\[\begin{align*} & \text{minimize: } \quad \frac{1}{2} ||\vec{w}||^{2} + C \sum\limits_{i=1}^{n} \xi_{i} \\ & \text{subject to: } \quad \begin{cases} y_{i} \big( \vec{w} \cdot \vec{x_{i}} - b \big) \geq 1 - \xi_{i}, \quad \forall i \in \mathbb{N}^{+} \\ \xi_{i} \geq 0, \qquad \qquad \qquad \qquad \forall i \in \mathbb{N}^{+} \\ \end{cases} \end{align*} \]

問題：如何求解最優的 \(\vec{w}, ~ b, ~ \vec{\xi}\) ？

由於涉及邊界問題，我們不能在目標函數中直接對 \(\vec{w}, ~ b, ~ \vec{\xi}\) 求偏導。我們有以下兩種解決辦法：

Projection Methods

從一個滿足 constraints 的解 \(\vec{x_{0}}\) 開始，求能使得 objective function 略微減小的 \(\vec{x_{1}}\)。如果所求到的 \(\vec{x_{1}}\) 違反了 constraints，那麼 project back to the constraints 進行迭代。這種方法偏向於利用演演算法求解，從原理上類似於梯度下降演演算法以及前文介紹的 Perceptron Algorithm。
Penalty Methods

使用懲罰函數將 constraints 併入 objective function，對於違反 constraints 的解 \(\vec{x}\) 予以懲罰。

The Lagrange (Penalty) Method：拉格朗日（懲罰）方法

考慮增廣函數：

\[L(\vec{x}, \vec{\lambda}) = f(\vec{x}) + \sum\limits_{i=1}^{n} \lambda_{i} g_{i}(\vec{x}) \]

其中，\(L(\vec{x}, \vec{\lambda})\) 為拉格朗日函數，\(\lambda_{i}\) 為拉格朗日變數（或對偶變數，dual variables）。

對於此類函數，我們所需要的目標的 canonical form 為：

\[\begin{align*} \text{minimize: } \quad & f(\vec{x}) \\ \text{subject to: } \quad & g_{i}(\vec{x}) \leq 0, \quad \forall i \in \mathbb{N}^{+} \end{align*} \]

由於 \(g_{i}(\vec{x}) \leq 0\) for \(\forall i \in \mathbb{N}^{+}\)，則對於任意的 feasible \(\vec{x}\) 以及任意的 \(\vec{\lambda_{i}} \geq 0\)，都有：

\[L(\vec{x}, \vec{\lambda}) \leq f(\vec{x}) \]

因此：

\[\max\limits_{\lambda_{i} \geq 0} L(\vec{x}, \vec{\lambda}) \leq f(\vec{x}) \]

注意到上式中的 \(\max\limits_{\lambda_{i} \geq 0} L(\vec{x}, \vec{\lambda})\)，這代表我們在 \(\vec{\lambda}\) 所在的空間 \([0, ~ \infty)^{n}\) 中搜尋使拉格朗日函數最大的 \(\vec{\lambda}\)，即搜尋各個對應的 \(\lambda_{i} \in [0, ~ \infty)\)。

尤其注意上式 是針對 feasible \(\vec{x}\) 成立。因為 \(\max\limits_{\lambda_{i} \geq 0} L(\vec{x}, \vec{\lambda})\) 會導致：

當 \(\vec{x}\) infeasible 時，意味著 \(\vec{x}\) 不全滿足所有約束條件 \(g_{i}(\vec{x}) \leq 0\) for \(\forall i \in \mathbb{N}^{+}\)，這意味著：

\[\exists i: ~ g_{i}(\vec{x}) > 0 \]

那麼：

\[\begin{align*} \max\limits_{\lambda_{i} \geq 0} L(\vec{x}, \vec{\lambda}) & = \max\limits_{\lambda_{i} \geq 0} \Big( f(\vec{x}) + \sum\limits_{i=1}^{n} \lambda_{i} g_{i}(\vec{x}) \Big) \\ & = f(\vec{x}) + \max\limits_{\lambda_{i} \geq 0} \sum\limits_{i=1}^{n} \lambda_{i} g_{i}(\vec{x}) \\ & = \infty \end{align*} \]

這是因為：只要對應的 \(\lambda_{i} \rightarrow \infty\)，則 \(\lambda_{i} g_{i}(\vec{x}) \rightarrow \infty\)（因為 \(g_{i}(\vec{x}) > 0\)），從而 \(\sum\limits_{i=1}^{n} \lambda_{i} g_{i}(\vec{x}) \rightarrow \infty\)，故 \(L(\vec{x}, \vec{\lambda}) = f(\vec{x}) + \sum\limits_{i=1}^{n} \lambda_{i} g_{i}(\vec{x}) \rightarrow \infty\)。

所以此時不滿足 \(\max\limits_{\lambda_{i} \geq 0} L(\vec{x}, \vec{\lambda}) \leq f(\vec{x})\)。
當 \(\vec{x}\) feasible 時，即對於 \(\forall i \in \mathbb{N}^{+}\)，約束條件 \(g_{i}(\vec{x}) \leq 0\) 都成立，那麼：

\[\forall i \in \mathbb{N}^{+}: ~ g_{i}(\vec{x}) \quad \implies \quad\sum\limits_{i=1}^{n} \lambda_{i} g_{i}(\vec{x}) \leq 0 \]

因此 \(\max\limits_{\lambda_{i} \geq 0} \sum\limits_{i=1}^{n} \lambda_{i} g_{i}(\vec{x}) = 0\)，即令所有 \(\lambda_{i}\) 都為 \(0\)，故：

\[\begin{align*} \max\limits_{\lambda_{i} \geq 0} L(\vec{x}, \vec{\lambda}) & = \max\limits_{\lambda_{i} \geq 0} \Big( f(\vec{x}) + \sum\limits_{i=1}^{n} \lambda_{i} g_{i}(\vec{x}) \Big) \\ & = f(\vec{x}) + \max\limits_{\lambda_{i} \geq 0} \Big( \sum\limits_{i=1}^{n} \lambda_{i} g_{i}(\vec{x}) \Big) \\ & = f(\vec{x}) \end{align*} \]

根據上述結論，給定任意 feasible \(\vec{x}\) 以及任意 \(\lambda_{i} \geq 0\)，有：