Ceres 自動求導解析-從原理到實踐
2023-04-01 18:00:12
Ceres 自動求導解析-從原理到實踐
目錄
1.0 前言
Ceres 有一個自動求導功能，只要你按照Ceres要求的格式寫好目標函數，Ceres會自動幫你計算精確的導數（或者雅克比矩陣），這極大節約了演演算法開發者的時間，但是筆者在使用的時候一直覺得這是個黑盒子，特別是之前在做深度學習的時候，神經網路本事是一個很盒模型了，再加上 pytorch 的自動求導，簡直是黑上加黑。現在轉入視覺SLAM方向，又碰到了 Ceres 的自動求導，是時候揭開其真實的面紗了。知其然並知其所以然才是一名演演算法工程師應有的基本素養。
2.0 Ceres求導簡介
Ceres 一共有三種求導的方式提供給開發者，分別是：
-
解析求導，也就是手動計算出導數的解析形式。
例如有如下函數;
\[y = \frac{b_1}{(1+e^{b_2-b_3x})^{1/b_4}} \]構建誤差函數：
\[\begin{split}\begin{align} E(b_1, b_2, b_3, b_4) &= \sum_i f^2(b_1, b_2, b_3, b_4 ; x_i, y_i)\\ &= \sum_i \left(\frac{b_1}{(1+e^{b_2-b_3x_i})^{1/b_4}} - y_i\right)^2\\ \end{align}\end{split} \]對待優化變數的導數為：
\[\begin{split}\begin{align} D_1 f(b_1, b_2, b_3, b_4; x,y) &= \frac{1}{(1+e^{b_2-b_3x})^{1/b_4}}\\ D_2 f(b_1, b_2, b_3, b_4; x,y) &= \frac{-b_1e^{b_2-b_3x}}{b_4(1+e^{b_2-b_3x})^{1/b_4 + 1}} \\ D_3 f(b_1, b_2, b_3, b_4; x,y) &= \frac{b_1xe^{b_2-b_3x}}{b_4(1+e^{b_2-b_3x})^{1/b_4 + 1}} \\ D_4 f(b_1, b_2, b_3, b_4; x,y) & = \frac{b_1 \log\left(1+e^{b_2-b_3x}\right) }{b_4^2(1+e^{b_2-b_3x})^{1/b_4}} \end{align}\end{split} \] -
數值求導，當對變數增加一個微小的增量，然後觀察此時的殘差和原先殘差的下降比例即可，其實就是導數的定義。
\[Df(x) = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \]當然其實也有兩種形式對導數進行數值上的近似，第一種是Forward Differences：
\[Df(x) \approx \frac{f(x + h) - f(x)}{h} \]第二種是 Central Differences：
\[Df(x) \approx \frac{f(x + h) - f(x - h)}{2h} \]Ceres 的官方檔案上是認為第二種比第一種好的，但是其實官方還介紹了第三種，這裡就不詳說了，感興趣的可以去看官方檔案：Ridders’ Method。
這裡有三種數值微分方法的效果對比，從右向左看：
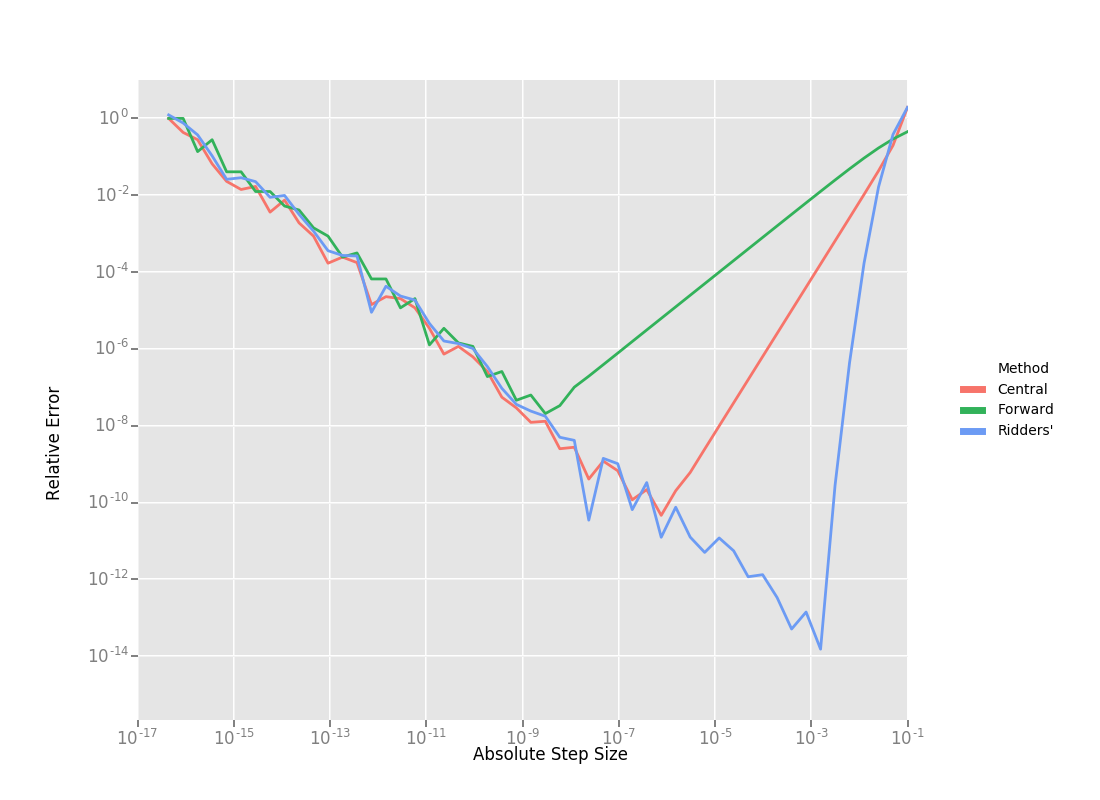
效果依次是 \(Ridders > Central > Forwad\)
- 第三種則是今天要介紹的主角，自動求導。
3.0 Ceres 自動求導原理
3.1 官方解釋
其實官方對自動求導做出瞭解釋，但是筆者覺得寫的不夠直觀，比較抽象，不過既然是官方出品，還是非常有必要去看一看的。http://ceres-solver.org/automatic_derivatives.html。
3.2 自我理解
\(\quad\)這裡筆者根據網上和官方的資料整理了一下自己的理解。Ceres 自動求導的核心是運運算元的過載與Ceres自有的 Jet 變數。
舉一個例子：
函數 \(\mathrm{f}(\mathrm{x})=\mathrm{h}(\mathrm{x}) * \mathrm{~g}(\mathrm{x})\) , 他的目標函數值為 \(\mathrm{h}(\mathrm{x}) * \mathrm{~g}(\mathrm{x})\) , 導數為
\[\mathrm{f}^{\prime}(\mathrm{x})=\mathrm{h}^{\prime}(\mathrm{x}) \mathrm{g}(\mathrm{x})+\mathrm{h}(\mathrm{x}) \mathrm{g}^{\prime}(\mathrm{x})
\]
其中 \(h(x)\), \(g(x)\) 都是標量函數.
如果我們定義一種資料型別,
\[Data \{ double\ \ value, double\ \ derived \}
\]
並且對於資料型別 Data，過載乘法運運算元
\[data1*data2=\begin{bmatrix}
data1.value*data2.value \\
data1.derived*data2.value+data1.value*data2.derived
\end{bmatrix}
\]
令 \(h(x) =[h(x),{h(x)}' ] , g(x)=[g(x),{g(x)' }]\)。\(f(x)=h(x) * g(x)\), 那麼f_x.derived 就是\(f(x)\)的導數，f_x.value 即為\(f(x)\)的數值。value 儲存變數的函數值, derived 儲存變數對 \(\mathrm{x}\) 的導數。類似，如果我們對資料型別 Data 過載所有可能用到的運運算元. 「\(+- * / \log , \exp , \cdots\)」 。那麼在變數 \(h(x),g(x)\)經過任意次運算後，\(result=h(x)+g(x)*h(x)+exp(h(x))…\), 任然能獲得函數值 result.value 和他的導數值 result.derived，這就是Ceres 自動求導的原理。
上面講的都是單一自變數的自動求導，對於多元函數\(f(x_i)\)。對於n 元函數，Data 裡面的 double derived 就替換為 double* derived，derived[i] 為對於第i個自變數的導數值。
並且對於資料型別 Data，乘法運運算元過載為
\[data1*data2=\begin{bmatrix}
data1.value*data2.value \\
derived[i]=data1.derived[i]*data2.value+data1.value*data2.derived[i]
\end{bmatrix}
\]
其餘的運運算元過載方法也做相應改變。這樣對多元函數的自動求導問題也就解決了。Ceres 裡面的Jet 資料型別類似於 這裡Data 型別，並且Ceres 對Jet 資料型別進行了幾乎所有數學運運算元的過載，以達到自動求導的目的。
4.0 實踐
4.1 Jet 的實現
這裡我們模仿 Ceres 實現了 Jet ，並準備了兩個具體的範例程式，Jet 具體程式碼在 ceres_jet.hpp 中，包裝成了一個標頭檔案，在使用的時候進行呼叫即可。這裡也包含了一個 ceres_rotation.hpp 的標頭檔案，是為了我們的第二個例子實現。具體程式碼如下：
ceres_jet.hpp
#ifndef _CERES_JET_HPP__
#define _CERES_JET_HPP__
#include <math.h>
#include <stdio.h>
#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Dense>
#include <eigen3/Eigen/Sparse>
#include "eigen3/Eigen/Eigen"
#include "eigen3/Eigen/SparseQR"
#include <fstream>
#include <iostream>
#include <map>
#include <queue>
#include <set>
#include <vector>
#include "ceres_rotation.hpp"
#include "algorithm"
#include "stdlib.h"
template <int N>
struct jet
{
Eigen::Matrix<double, N, 1> v;
double a;
jet() : a(0.0) {}
jet(const double& value) : a(value) { v.setZero(); }
EIGEN_STRONG_INLINE jet(const double& value,
const Eigen::Matrix<double, N, 1>& v_)
: a(value), v(v_)
{
}
jet(const double value, const int index)
{
v.setZero();
a = value;
v(index, 0) = 1.0;
}
void init(const double value, const int index)
{
v.setZero();
a = value;
v(index, 0) = 1.0;
}
};
/****************jet overload******************/
// for the camera BA,the autodiff only need overload the operator :jet+jet
// number+jet -jet jet-number jet*jet number/jet jet/jet sqrt(jet) cos(jet)
// sin(jet) +=(jet) overload jet + jet
template <int N>
inline jet<N> operator+(const jet<N>& A, const jet<N>& B)
{
return jet<N>(A.a + B.a, A.v + B.v);
} // end jet+jet
// overload number + jet
template <int N>
inline jet<N> operator+(double A, const jet<N>& B)
{
return jet<N>(A + B.a, B.v);
} // end number+jet
template <int N>
inline jet<N> operator+(const jet<N>& B, double A)
{
return jet<N>(A + B.a, B.v);
} // end number+jet
// overload jet-number
template <int N>
inline jet<N> operator-(const jet<N>& A, double B)
{
return jet<N>(A.a - B, A.v);
}
// overload number * jet because jet *jet need A.a *B.v+B.a*A.v.So the number
// *jet is required
template <int N>
inline jet<N> operator*(double A, const jet<N>& B)
{
return jet<N>(A * B.a, A * B.v);
}
template <int N>
inline jet<N> operator*(const jet<N>& A, double B)
{
return jet<N>(B * A.a, B * A.v);
}
// overload -jet
template <int N>
inline jet<N> operator-(const jet<N>& A)
{
return jet<N>(-A.a, -A.v);
}
template <int N>
inline jet<N> operator-(double A, const jet<N>& B)
{
return jet<N>(A - B.a, -B.v);
}
template <int N>
inline jet<N> operator-(const jet<N>& A, const jet<N>& B)
{
return jet<N>(A.a - B.a, A.v - B.v);
}
// overload jet*jet
template <int N>
inline jet<N> operator*(const jet<N>& A, const jet<N>& B)
{
return jet<N>(A.a * B.a, B.a * A.v + A.a * B.v);
}
// overload number/jet
template <int N>
inline jet<N> operator/(double A, const jet<N>& B)
{
return jet<N>(A / B.a, -A * B.v / (B.a * B.a));
}
// overload jet/jet
template <int N>
inline jet<N> operator/(const jet<N>& A, const jet<N>& B)
{
// This uses:
//
// a + u (a + u)(b - v) (a + u)(b - v)
// ----- = -------------- = --------------
// b + v (b + v)(b - v) b^2
//
// which holds because v*v = 0.
const double a_inverse = 1.0 / B.a;
const double abyb = A.a * a_inverse;
return jet<N>(abyb, (A.v - abyb * B.v) * a_inverse);
}
// sqrt(jet)
template <int N>
inline jet<N> sqrt(const jet<N>& A)
{
double t = std::sqrt(A.a);
return jet<N>(t, 1.0 / (2.0 * t) * A.v);
}
// cos(jet)
template <int N>
inline jet<N> cos(const jet<N>& A)
{
return jet<N>(std::cos(A.a), -std::sin(A.a) * A.v);
}
template <int N>
inline jet<N> sin(const jet<N>& A)
{
return jet<N>(std::sin(A.a), std::cos(A.a) * A.v);
}
template <int N>
inline bool operator>(const jet<N>& f, const jet<N>& g)
{
return f.a > g.a;
}
#endif //_CERES_JET_HPP__
ceres_rotation.hpp
#ifndef CERES_ROTATION_HPP_
#define CERES_ROTATION_HPP_
#include <iostream>
template <typename T>
inline T DotProduct(const T x[3], const T y[3])
{
return (x[0] * y[0] + x[1] * y[1] + x[2] * y[2]);
}
template <typename T>
inline void AngleAxisRotatePoint(const T angle_axis[3], const T pt[3],
T result[3])
{
const T theta2 = DotProduct(angle_axis, angle_axis);
if (theta2 > T(std::numeric_limits<double>::epsilon()))
{
// Away from zero, use the rodriguez formula
//
// result = pt costheta +
// (w x pt) * sintheta +
// w (w . pt) (1 - costheta)
//
// We want to be careful to only evaluate the square root if the
// norm of the angle_axis vector is greater than zero. Otherwise
// we get a division by zero.
//
const T theta = sqrt(theta2);
const T costheta = cos(theta);
const T sintheta = sin(theta);
const T theta_inverse = T(1.0) / theta;
const T w[3] = {angle_axis[0] * theta_inverse,
angle_axis[1] * theta_inverse,
angle_axis[2] * theta_inverse};
// Explicitly inlined evaluation of the cross product for
// performance reasons.
const T w_cross_pt[3] = {w[1] * pt[2] - w[2] * pt[1],
w[2] * pt[0] - w[0] * pt[2],
w[0] * pt[1] - w[1] * pt[0]};
const T tmp =
(w[0] * pt[0] + w[1] * pt[1] + w[2] * pt[2]) * (T(1.0) - costheta);
result[0] = pt[0] * costheta + w_cross_pt[0] * sintheta + w[0] * tmp;
result[1] = pt[1] * costheta + w_cross_pt[1] * sintheta + w[1] * tmp;
result[2] = pt[2] * costheta + w_cross_pt[2] * sintheta + w[2] * tmp;
}
else
{
// Near zero, the first order Taylor approximation of the rotation
// matrix R corresponding to a vector w and angle w is
//
// R = I + hat(w) * sin(theta)
//
// But sintheta ~ theta and theta * w = angle_axis, which gives us
//
// R = I + hat(w)
//
// and actually performing multiplication with the point pt, gives us
// R * pt = pt + w x pt.
//
// Switching to the Taylor expansion near zero provides meaningful
// derivatives when evaluated using Jets.
//
// Explicitly inlined evaluation of the cross product for
// performance reasons.
const T w_cross_pt[3] = {angle_axis[1] * pt[2] - angle_axis[2] * pt[1],
angle_axis[2] * pt[0] - angle_axis[0] * pt[2],
angle_axis[0] * pt[1] - angle_axis[1] * pt[0]};
result[0] = pt[0] + w_cross_pt[0];
result[1] = pt[1] + w_cross_pt[1];
result[2] = pt[2] + w_cross_pt[2];
}
}
#endif // CERES_ROTATION_HPP_
4.2 多項式函數自動求導
這裡我們準備了兩個實踐案例，一個是對下面的函數進行自動求導，求在 \(f(1,2)\) 處的導數。
\[f(x,y)=2x^2+3y^3+3
\]
程式碼如下：
#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Dense>
#include "ceres_jet.hpp"
int main(int argc, char const *argv[])
{
/// f(x,y) = 2*x^2 + 3*y^3 + 3
/// 殘差的維度，變數1的維度，變數2的維度
const int N = 1, N1 = 1, N2 = 1;
Eigen::Matrix<double, N, N1> jacobian_parameter1;
Eigen::Matrix<double, N, N2> jacobian_parameter2;
Eigen::Matrix<double, N, 1> jacobi_residual;
/// 模板引數為向量的維度，一定要是 N1+N2
/// 也就是總的變數的維度，因為要儲存結果（殘差）
/// 對於每個變數的導數值
/// 至於為什麼有 N1 個 jet 表示 var_x
/// 假設變數 1 的維度為 N1,則殘差對該變數的導數的維度是一個 N*N1 的矩陣
/// 一個 jet<N1 + N2> 只能表示變數中的某一個在當前點的導數和值
jet<N1 + N2> var_x[N1];
jet<N1 + N2> var_y[N2];
jet<N1 + N2> residual[N];
/// 假設我們求上面的方程在 (x,y)->(1.0,2.0) 處的導數值
double var_x_init_value[N1] = {1.0};
double var_y_init_value[N1] = {2.0};
for (int i = 0; i < N1; i++)
{
var_x[i].init(var_x_init_value[i], i);
}
for (int i = 0; i < N2; i++)
{
var_y[i].init(var_y_init_value[i], i + N1);
}
/// f(x,y) = 2*x^2 + 3*y^3 + 3
/// f_x` = 4x
/// f_y` = 9 * y^2
residual[0] = 2.0 * var_x[0] * var_x[0] + 3.0 * var_y[0] * var_y[0] * var_y[0] + 3.0;
std::cout << "residual: " << residual[0].a << std::endl;
std::cout << "jacobian: " << residual[0].v.transpose() << std::endl;
/// residual: 29
/// jacobian: 4 36
return 0;
}
-
輸出結果，讀者可以自己求導算一下，是正確的。
residual: 29 jacobian: 4 36
4.3 BA 問題中的自動求導
這裡是用的 Bal 資料集中的某個觀測構建的誤差項求導
#include "ceres_jet.hpp"
class costfunction
{
public:
double x_;
double y_;
costfunction(double x, double y) : x_(x), y_(y) {}
template <class T>
void Evaluate(const T* camera, const T* point, T* residual)
{
T result[3];
AngleAxisRotatePoint(camera, point, result);
result[0] = result[0] + camera[3];
result[1] = result[1] + camera[4];
result[2] = result[2] + camera[5];
T xp = -result[0] / result[2];
T yp = -result[1] / result[2];
T r2 = xp * xp + yp * yp;
T distortion = 1.0 + r2 * (camera[7] + camera[8] * r2);
T predicted_x = camera[6] * distortion * xp;
T predicted_y = camera[6] * distortion * yp;
residual[0] = predicted_x - x_;
residual[1] = predicted_y - y_;
}
};
int main(int argc, char const* argv[])
{
const int N = 2, N1 = 9, N2 = 3;
Eigen::Matrix<double, N, N1> jacobi_parameter_1;
Eigen::Matrix<double, N, N2> jacobi_parameter_2;
Eigen::Matrix<double, N, 1> jacobi_residual;
costfunction* costfunction_ = new costfunction(-3.326500e+02, 2.620900e+02);
jet<N1 + N2> cameraJet[N1];
jet<N1 + N2> pointJet[N2];
double params_1[N1] = {
1.5741515942940262e-02, -1.2790936163850642e-02, -4.4008498081980789e-03,
-3.4093839577186584e-02, -1.0751387104921525e-01, 1.1202240291236032e+00,
3.9975152639358436e+02, -3.1770643852803579e-07, 5.8820490534594022e-13};
double params_2[N2] = {-0.612000157172, 0.571759047760, -1.847081276455};
for (int i = 0; i < N1; i++)
{
cameraJet[i].init(params_1[i], i);
}
for (int i = 0; i < N2; i++)
{
pointJet[i].init(params_2[i], i + N1);
}
jet<N1 + N2>* residual = new jet<N1 + N2>[N];
costfunction_->Evaluate(cameraJet, pointJet, residual);
for (int i = 0; i < N; i++)
{
jacobi_residual(i, 0) = residual[i].a;
}
for (int i = 0; i < N; i++)
{
jacobi_parameter_1.row(i) = residual[i].v.head(N1);
jacobi_parameter_2.row(i) = residual[i].v.tail(N2);
}
/*
real result:
jacobi_parameter_1:
-283.512 -1296.34 -320.603 551.177 0.000204691 -471.095 -0.854706 -409.362 -490.465
1242.05 220.93 -332.566 0.000204691 551.177 376.9 0.68381 327.511 392.397
jacobi_parameter_2:
545.118 -5.05828 -478.067
2.32675 557.047 368.163
jacobi_residual:
-9.02023
11.264
*/
std::cout << "jacobi_parameter_1: \n" << jacobi_parameter_1 << std::endl;
std::cout << "jacobi_parameter_2: \n" << jacobi_parameter_2 << std::endl;
std::cout << "jacobi_residual: \n" << jacobi_residual << std::endl;
delete (residual);
return 0;
}
-
輸出結果
jacobi_parameter_1: -283.512 -1296.34 -320.603 551.177 0.000204691 -471.095 -0.854706 -409.362 -490.465 1242.05 220.93 -332.566 0.000204691 551.177 376.9 0.68381 327.511 392.397 jacobi_parameter_2: 545.118 -5.05828 -478.067 2.32675 557.047 368.163 jacobi_residual: -9.02023 11.264
Reference
- http://ceres-solver.org/
- https://blog.csdn.net/u012260559/article/details/105878468
- https://www.ngui.cc/article/show-902862.html?action=onClick