列線圖作為一個非常簡單明瞭的臨床輔助決策工具，在臨床中用的（發文章的）還是比較多的，尤其是腫瘤預後：

Nomograms are widely used for cancer prognosis, primarily because of their ability to reduce statistical predictive models into a single numerical estimate of the probability of an event, such as death or recurrence, that is tailored to the profile of an individual patient.

找個公開資料庫做生存分析出個列線圖，然後出個文章是很多臨床同學可以依賴的較容易的實現路徑，之前有給大家介紹過列線圖，今天開始再給大家比較詳細地寫寫生存分析列線圖系列，希望可以對大家有幫助。

理解列線圖

要弄明白生存分析的列線圖的出圖邏輯。我們首先來回顧下cox模型究竟是擬合是什麼東西，看下圖：

在基礎風險確定後，乘上以e為底數的指數函數（我們關心的協變數的線性部分是在指數上）就可以得到風險函數（為什麼能這麼做就涉及到比例風險假設）。通過線性部分的指數函數和基礎風險我們cox模型最終得到的是hazard function。

通過hazard function我們可以得到hazard rate，但是對於臨床應用來講，臨床醫師關心的東西更直觀，他們關心的是具體協變數條件下個體的生存概率，畫出的列線圖常常如下面所示：

列線圖中的結局常常是某個時間點的生存概率，這就要求我們在統計處理上做出轉換。就是將風險函數轉換成生存函數進而得到預測的生存概率。

接下來我們就來詳細地過一遍實操重點。

本文中涉及到的文獻圖片和方法描述均來自JAMA Surg雜誌的文章，文章參照如下：

Hyder O, Marques H, Pulitano C, et al. A Nomogram to Predict Long-term Survival After Resection for Intrahepatic Cholangiocarcinoma: An Eastern and Western Experience. JAMA Surg. 2014;149(5):432–438. doi:10.1001/jamasurg.2013.5168

變數選擇

首先看變數篩選，經常我們用來做模型的資料庫中有很多變數，列線圖作為一個臨床應用工具，變數肯定是越少越好的（讓醫生算分算半個多小時總分總是不合適推廣的嘛，雖然大家做論文都不關心臨床轉換，但是還要有這個意識比較好），所以必須精選，這篇文章用到的方法叫做Backward stepwise selection：

Backward stepwise selection using the AIC in Cox proportional hazards regression modeling identified 6 variables that were the most associated with survival: age, tumor size, multiple lesions, nodal status, vascular invasion, and presence of cirrhosis of the underlying liver

我看生存分析列線圖的文章這個方法用得還是比較普遍的哈，基本都是單變數篩過之後再來個stepwise selection：

整體這個方法在R中操作也是非常方便的，像rms包中專門就有fastbw函數進行倒退法的逐步篩選。

可以用aic為標準，也可以用p值為標準進行篩，很方便的。

用生存分析模型出列線圖

首先明確，同學們不要再稱呼「列線圖模型」了，列線圖只是具體模型的視覺化、工具化表示，他本身不是模型。模型本身具體要看你到底做的是什麼統計模型，比如邏輯模型，比如線性迴歸模型，再比如今天寫的COX模型，這個才叫模型。

A nomogram is a graphical representation of a mathematical model involving several pre- dictors to predict a particular endpoint based on traditional statistical methods such as Cox proportional hazards model for survival data or logistic regression for binary outcome

好多同學問我能不能幫忙做一個列線圖模型，其實這種表達我是摸不著頭腦的。

出列線圖，首先要確定內在的統計模型，比如今天寫生存資料的列線圖，我就要先做一個COX模型，然後再借助nomogram函數出圖，這個函數的引數很多，下圖只是部分引數：

可以看到這個函數需要的第一個引數就是一個做好的模型fit。具體到生存分析的列線圖，我們就需要先跑一個cox模型出來，然後對跑模型的資料集d進行下面的操作：

ddist <- datadist(d); options(datadist='ddist')

生存分析的列線圖需要調節的地方可以有很多。

比如我們做一個生存分析，在nomogram函數中不設定任何引數直接去出列線圖的話，出出來的圖是這樣的：

圖中只會有cox模型線性部分的預測值，這個時候我們需要將線性預測值轉換為生存概率才符合臨床應用實際，就像下圖發表中的文獻一樣：

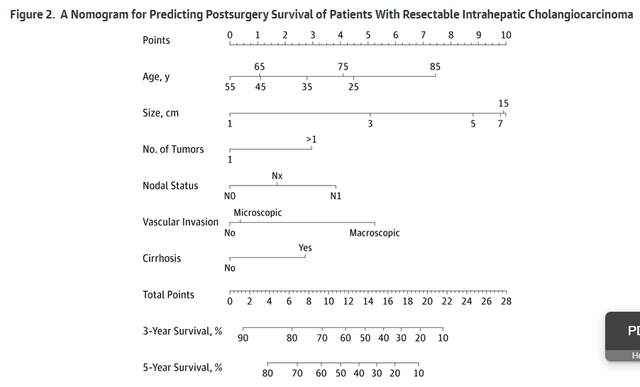
此時要做的就是進行風險函數和生存概率函數的轉換。我們需要設定轉換的程式碼如下：

surv <- Survival(f)

通過上面的程式碼我們就可以將cph函數擬合出來的風險函數轉換成生存函數，從而在列線圖的繪製中我們可以規定顯示具有臨床意義的時間點的某個個體的生存概率。比如我想得到3年和6年的生存概率為結局的列線圖，我就可以寫出如下程式碼：

plot(nomogram(f, fun=list(function(x) surv(3, x),
                            function(x) surv(6, x)),
            funlabel=c("age 3 Survival Probability", 
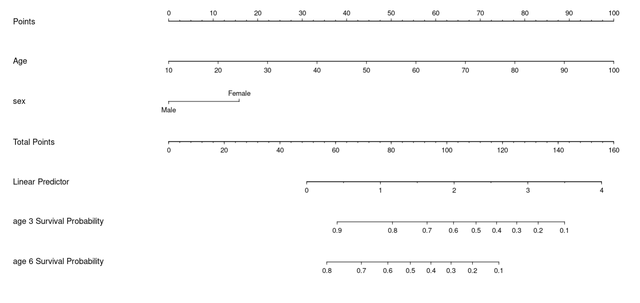
                       "age 6 Survival Probability"))

上面的程式碼中f是cph物件，fun中給定的就是將線性預測值轉換成生存概率的函數，執行程式碼即可出圖如下：

並且針對nomogram可以做很多的個性化的修飾，比如lp引數可以控制是否顯示線性預測值的打分軸，lp.at和fun.at可以控制線性預測值打分軸和轉換函數顯示的點。比如對於上圖，我希望線性預測值的軸只顯示0到4的點，我就可以寫引數：

lp.at = c(0,1,2,3,4)

就可以實現。

還有，有時候我們分類變數的水平比較多，名字比較長，我們可能會將abbrev引數設定為TRUE來縮略顯示長度，比如你注意下面的圖和上面的在sex水平上的顯示區別就是因為我們將abbrev引數設定為了T：

我們還可以很方便地改變列線圖的軸標籤，只需要將變數打上我們想要的標籤，比如將兩個變數標籤分別設定為「關注」和「Codewar」後，將下面的引數在nomogram函數中設定一下：

vnames='labels'

執行後檢視效果：

對於上面的列線圖，我可能還覺得我們的圖軸和標籤離得有點遠，這個時候我就可以將xfrac設定小一點比如我設定為0.2，這個時候圖就會緊湊很多；我們還可以通過tcl引數設定軸的刻度標線的長度，比如我設定為1，這時候圖的刻度線就會變長，讀圖就會更輕鬆。

xfrac=.2,tcl=1

引數像上面設定後，我們的圖就如下所示：

調了一下還是蠻有效果的哈，但是我還是不滿意，看人家jama的列線圖，背景色都有，淡淡的藍色顯得就很高階，這個操作大家只需要在出圖前設定：

par(bg = "aliceblue")

然後再plot效果就有了：

這下一看就是高分雜誌的的圖，背景色中的aliceblue你也可以任意改成你喜歡的顏色。

nomogram函數還有很多的引數可調，一篇文章肯定是寫不完的，其餘的調節功能留給大家自己探索了吧。

接下來寫讀圖的部分。

學會讀圖

為了更加的加深大家對模型本身和列線圖這個視覺化工具的區別的理解，我們今天帶大家結合cox模型來讀cox模型的列線圖。

首先我們學會讀線性預測值，首先再一次回憶模型的表達：

線性部分就是表示式中指數函數的指數部分，比如我現在跑了一個cox模型結果如下：

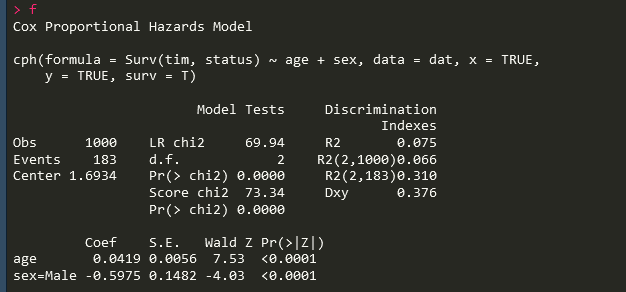
那麼我知道age的線性係數0.0419，sex中male的線性係數是-0.5975 ，所以我們的模型對一個10歲的男性線性部分預測值就應該為10*0.0419-0.5975=-0.178，回到我們這個模型的列線圖中

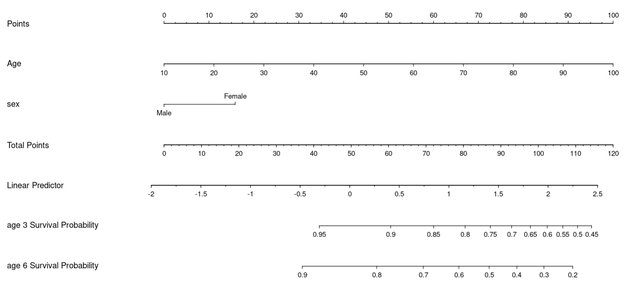
回到列線圖：我們可以看到10歲的得分是0分，男性得分為0，總分0分，對應的線性預測值大概也為-0.18（大家可以用尺子比個大概哈），達成一致。

我們再看生存概率的讀法，比如對於一個100歲的男人來講，依照下面的列線圖，她的年齡得分應該是100，性別得分是0，總分是100，對應的3年的生存概率應該大約是0.62（大家可以用把尺子比對下哈）：

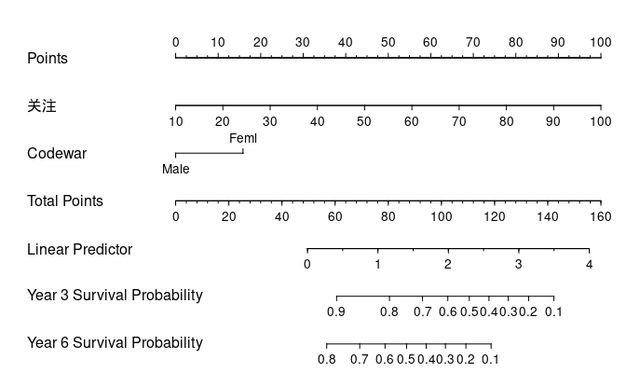
然後我們出列線圖的內在模型再一次驗證，我們用predictSurvProb函數，將新資料設定為1個100歲的男性，times設定為3，用原來的cox模型預測出來的生存概率確實也是0.627。依然達成一致。

上面就是讀圖方法與模型結果的相互驗證，希望能夠進一步加深列線圖只是模型的視覺化的表示這一概念的理解。

好了，今天的文章重點就放在列線圖出圖上，文章中還有報告決策曲線和校準曲線，C指數等下一次再給大家詳細寫。