動手造輪子自己實現人工智慧神經網路(ANN),解決鳶尾花分類問題Golang1.18實現
人工智慧神經網路( Artificial Neural Network,又稱為ANN)是一種由人工神經元組成的網路結構,神經網路結構是所有機器學習的基本結構,換句話說,無論是深度學習還是強化學習都是基於神經網路結構進行構建。關於人工神經元,請參見:人工智慧機器學習底層原理剖析,人造神經元,您一定能看懂,通俗解釋把AI「黑話」轉化為「白話文」。
機器學習可以解決什麼問題
機器學習可以幫助我們解決兩大類問題:迴歸問題和分類問題,它們的主要區別在於輸出變數的型別和預測目標的不同。
在迴歸問題中,輸出變數是連續值,預測目標是預測一個數值。例如,預測房價、預測銷售額等都是迴歸問題。通常使用迴歸模型,如線性迴歸、決策樹迴歸、神經網路迴歸等來解決這類問題。迴歸問題的評估指標通常是均方誤差(Mean Squared Error,MSE)、平均絕對誤差(Mean Absolute Error,MAE)等。
在分類問題中,輸出變數是離散值,預測目標是將樣本劃分到不同的類別中。例如,預測郵件是否是垃圾郵件、預測影象中的物體類別等都是分類問題。通常使用分類模型,如邏輯迴歸、決策樹分類、支援向量機、神經網路分類等來解決這類問題。分類問題的評估指標通常是準確率、精度(Precision)、召回率(Recall)等。
事實上,機器學習只能解決「可以」被解決的問題,也就是說,機器學習能幫我們做的是提高解決問題的效率,而不是解決我們本來解決不了的問題,說白了,機器學習只能解決人目前能解決的問題,比如說人現在不能做什麼?人不能永生,不能白日飛昇,也不能治癒絕症,所以你指望機器學習解決此類問題,就是痴心妄想。
同時,機器學習輸入的特徵引數和輸出的預期結果必須有邏輯相關性,什麼意思?比如說我們想預測房價,結果特徵引數輸入了很多沒有任何邏輯相關性的資料,比如歷年水稻的出產率,這就是沒有邏輯相關性的資料,這樣的問題再怎麼調參也是無法通過機器學習來解決的。
此外,迴歸問題中有一個領域非常引人關注,那就是預測股票價格,國內經常有人說自己訓練的模型可以預測某支A股的價格走勢,甚至可以精準到具體價格單位。說實話,挺滑稽的,關鍵是還真有人相信靠機器學習能在A股市場大殺特殺。
因為,稍微有點投資經驗的人都知道,股票的歷史資料和未來某個時間點或者某個時間段的實際價格,並不存在因果關係,尤其像A股市場這種可被操控的黑盒環境,連具體特徵都是隱藏的,或者說特徵是什麼都是未知的,你以為的特徵只是你以為的,並不是市場或者政策以為的,所以你輸入之前十年或者二十年的歷史股票資料,你讓它預測,就是在搞笑,機器學習沒法幫你解決此類問題。
為什麼現在GPT模型現在這麼火?是因為它在NLP(自然語言分析)領域有了質的突破,可以通過巨量資料模型聯絡上下文關係生成可信度高的回答,而這個上下文關係,就是我們所謂的引數和預期結果的因果關係。
鳶尾花分類問題
鳶尾花分類問題是一個經典的機器學習問題,也是神經網路入門的常用案例之一。它的目標是通過鳶尾花的花萼長度、花萼寬度、花瓣長度和花瓣寬度這四個特徵來預測鳶尾花的品種,分為三種:山鳶尾(Iris Setosa)、變色鳶尾(Iris Versicolour)和維吉尼亞鳶尾(Iris Virginica)。

通俗來講,就是我們要訓練一個神經網路模型,它能夠根據鳶尾花的四個特徵,自動地對鳶尾花的品種進行分類。
在這個案例中,我們使用了一個包含一個隱藏層的神經網路,它的輸入層有4個神經元,代表鳶尾花的4個特徵;隱藏層有3個神經元;輸出層有3個神經元,分別代表3種鳶尾花的品種:
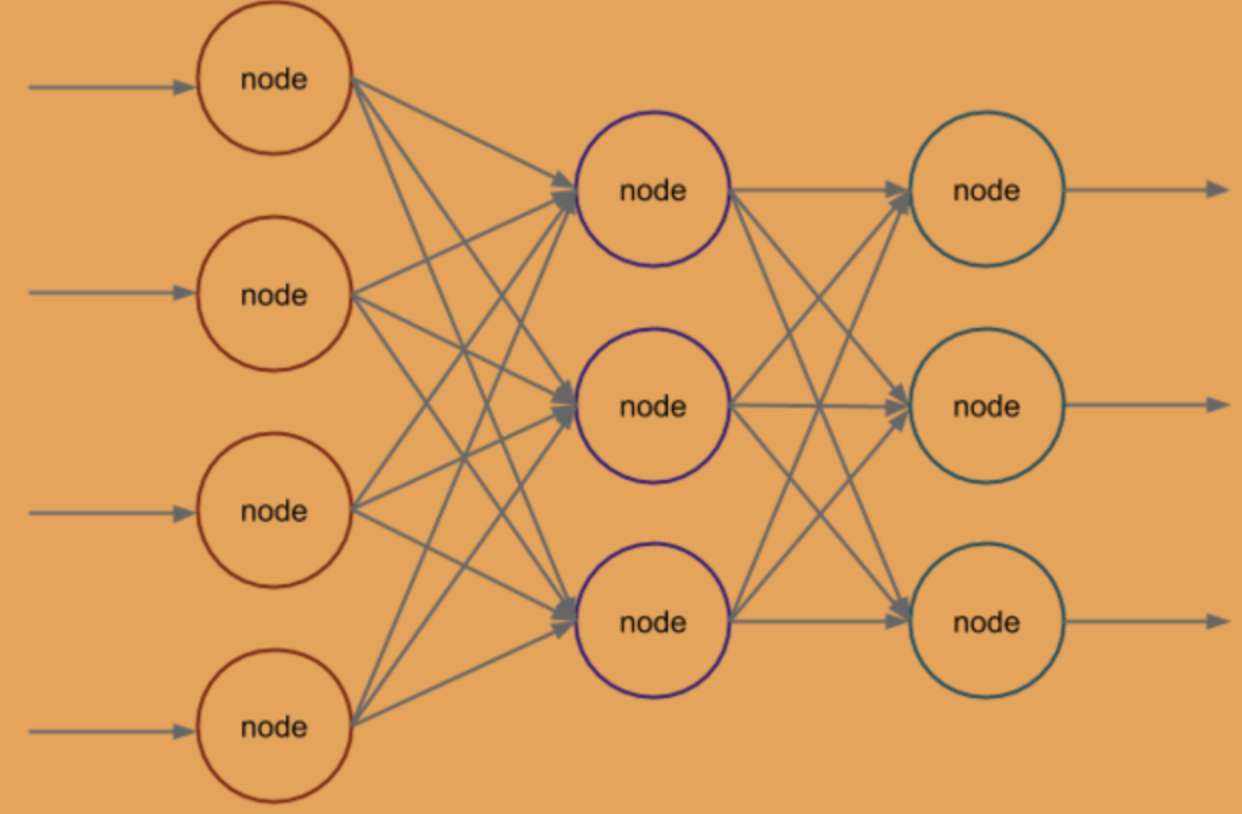
由此可見,神經網路通常由三層組成:輸入層、隱藏層和輸出層。
輸入層:輸入層接收外部輸入訊號,是神經網路的起點。它的神經元數量與輸入特徵的數量相同,每個神經元代表一個輸入特徵。輸入層的主要作用是將外部輸入轉換為神經網路內部的訊號。
隱藏層:隱藏層位於輸入層和輸出層之間,是神經網路的核心部分。它的神經元數量可以根據問題的複雜度自由設定,每個神經元接收上一層神經元輸出的訊號,並進行加權處理和啟用函數處理,再將結果傳遞給下一層神經元。隱藏層的主要作用是對輸入訊號進行復雜的非線性轉換,提取出輸入訊號中的特徵,從而使得神經網路能夠對複雜的問題進行處理。
輸出層:輸出層是神經網路的終點,它的神經元數量通常與問題的輸出數量相同。每個神經元代表一個輸出結果,輸出層的主要作用是將隱藏層處理後的訊號進行進一步處理,並將最終的結果輸出。
在神經網路中,輸入訊號從輸入層開始,通過隱藏層的處理,最終到達輸出層。每一層的神經元都與下一層的神經元相連,它們之間的連線可以看成是一種權重關係,權重值代表了兩個神經元之間的相關性強度。當神經網路接收到輸入訊號後,每個神經元都會對這些訊號進行加權處理,並通過啟用函數將結果輸出給下一層神經元,最終形成輸出結果。通過不斷調整權重和啟用函數,神經網路可以學習到輸入和輸出之間的複雜非線性關係,從而對未知資料進行預測和分類等任務。
定義神經網路結構體
在開始訓練之前,我們先定義一些需要的結構體和函數:
// neuralNet contains all of the information
// that defines a trained neural network.
type neuralNet struct {
config neuralNetConfig
wHidden *mat.Dense
bHidden *mat.Dense
wOut *mat.Dense
bOut *mat.Dense
}
// neuralNetConfig defines our neural network
// architecture and learning parameters.
type neuralNetConfig struct {
inputNeurons int
outputNeurons int
hiddenNeurons int
numEpochs int
learningRate float64
}
這裡neuralNet是神經網路結構體,同時定義輸入、隱藏和輸出層神經元的設定。
隨後宣告函數初始化神經網路:
func newNetwork(config neuralNetConfig) *neuralNet {
return &neuralNet{config: config}
}
這裡返回神經網路的指標。
除此之外,我們還需要定義啟用函數及其導數,這是在反向傳播過程中需要使用的。啟用函數有很多選擇,但在這裡我們將使用sigmoid函數。這個函數有很多優點,包括概率解釋和方便的導數表示式:
// sigmoid implements the sigmoid function
// for use in activation functions.
func sigmoid(x float64) float64 {
return 1.0 / (1.0 + math.Exp(-x))
}
// sigmoidPrime implements the derivative
// of the sigmoid function for backpropagation.
func sigmoidPrime(x float64) float64 {
return sigmoid(x) * (1.0 - sigmoid(x))
}
實現反向傳播
反向傳播是指在前向傳播之後,計算神經網路誤差並將誤差反向傳播到各層神經元中進行引數(包括權重和偏置)的更新。在反向傳播過程中,首先需要計算網路的誤差,然後通過鏈式法則將誤差反向傳播到各層神經元,以更新每個神經元的權重和偏置。這個過程也被稱為「反向梯度下降」,因為它是通過梯度下降演演算法來更新神經網路引數的。
說白了,反向傳播就是逆運算,用結果反推過程,這裡我們可以編寫一個實現反向傳播方法的方法,用於訓練或優化我們網路的權重和偏置。反向傳播方法包括以下步驟:
1 初始化權重和偏置(例如,隨機初始化)。
2 將訓練資料輸入神經網路中進行前饋,以生成輸出。
3 將輸出與正確輸出進行比較,以獲取誤差。
4 基於誤差計算權重和偏置的變化。
5 將變化通過神經網路進行反向傳播。
對於給定的迭代次數或滿足停止條件時,重複步驟2-5。
在步驟3-5中,我們將利用隨機梯度下降(SGD)來確定權重和偏置的更新:
// train trains a neural network using backpropagation.
func (nn *neuralNet) train(x, y *mat.Dense) error {
// Initialize biases/weights.
randSource := rand.NewSource(time.Now().UnixNano())
randGen := rand.New(randSource)
wHidden := mat.NewDense(nn.config.inputNeurons, nn.config.hiddenNeurons, nil)
bHidden := mat.NewDense(1, nn.config.hiddenNeurons, nil)
wOut := mat.NewDense(nn.config.hiddenNeurons, nn.config.outputNeurons, nil)
bOut := mat.NewDense(1, nn.config.outputNeurons, nil)
wHiddenRaw := wHidden.RawMatrix().Data
bHiddenRaw := bHidden.RawMatrix().Data
wOutRaw := wOut.RawMatrix().Data
bOutRaw := bOut.RawMatrix().Data
for _, param := range [][]float64{
wHiddenRaw,
bHiddenRaw,
wOutRaw,
bOutRaw,
} {
for i := range param {
param[i] = randGen.Float64()
}
}
// Define the output of the neural network.
output := new(mat.Dense)
// Use backpropagation to adjust the weights and biases.
if err := nn.backpropagate(x, y, wHidden, bHidden, wOut, bOut, output); err != nil {
return err
}
// Define our trained neural network.
nn.wHidden = wHidden
nn.bHidden = bHidden
nn.wOut = wOut
nn.bOut = bOut
return nil
}
接著實現具體的反向傳播邏輯:
// backpropagate completes the backpropagation method.
func (nn *neuralNet) backpropagate(x, y, wHidden, bHidden, wOut, bOut, output *mat.Dense) error {
// Loop over the number of epochs utilizing
// backpropagation to train our model.
for i := 0; i < nn.config.numEpochs; i++ {
// Complete the feed forward process.
hiddenLayerInput := new(mat.Dense)
hiddenLayerInput.Mul(x, wHidden)
addBHidden := func(_, col int, v float64) float64 { return v + bHidden.At(0, col) }
hiddenLayerInput.Apply(addBHidden, hiddenLayerInput)
hiddenLayerActivations := new(mat.Dense)
applySigmoid := func(_, _ int, v float64) float64 { return sigmoid(v) }
hiddenLayerActivations.Apply(applySigmoid, hiddenLayerInput)
outputLayerInput := new(mat.Dense)
outputLayerInput.Mul(hiddenLayerActivations, wOut)
addBOut := func(_, col int, v float64) float64 { return v + bOut.At(0, col) }
outputLayerInput.Apply(addBOut, outputLayerInput)
output.Apply(applySigmoid, outputLayerInput)
// Complete the backpropagation.
networkError := new(mat.Dense)
networkError.Sub(y, output)
slopeOutputLayer := new(mat.Dense)
applySigmoidPrime := func(_, _ int, v float64) float64 { return sigmoidPrime(v) }
slopeOutputLayer.Apply(applySigmoidPrime, output)
slopeHiddenLayer := new(mat.Dense)
slopeHiddenLayer.Apply(applySigmoidPrime, hiddenLayerActivations)
dOutput := new(mat.Dense)
dOutput.MulElem(networkError, slopeOutputLayer)
errorAtHiddenLayer := new(mat.Dense)
errorAtHiddenLayer.Mul(dOutput, wOut.T())
dHiddenLayer := new(mat.Dense)
dHiddenLayer.MulElem(errorAtHiddenLayer, slopeHiddenLayer)
// Adjust the parameters.
wOutAdj := new(mat.Dense)
wOutAdj.Mul(hiddenLayerActivations.T(), dOutput)
wOutAdj.Scale(nn.config.learningRate, wOutAdj)
wOut.Add(wOut, wOutAdj)
bOutAdj, err := sumAlongAxis(0, dOutput)
if err != nil {
return err
}
bOutAdj.Scale(nn.config.learningRate, bOutAdj)
bOut.Add(bOut, bOutAdj)
wHiddenAdj := new(mat.Dense)
wHiddenAdj.Mul(x.T(), dHiddenLayer)
wHiddenAdj.Scale(nn.config.learningRate, wHiddenAdj)
wHidden.Add(wHidden, wHiddenAdj)
bHiddenAdj, err := sumAlongAxis(0, dHiddenLayer)
if err != nil {
return err
}
bHiddenAdj.Scale(nn.config.learningRate, bHiddenAdj)
bHidden.Add(bHidden, bHiddenAdj)
}
return nil
}
接著宣告一個工具函數,它幫助我們沿一個矩陣維度求和,同時保持另一個維度不變:
// sumAlongAxis sums a matrix along a particular dimension,
// preserving the other dimension.
func sumAlongAxis(axis int, m *mat.Dense) (*mat.Dense, error) {
numRows, numCols := m.Dims()
var output *mat.Dense
switch axis {
case 0:
data := make([]float64, numCols)
for i := 0; i < numCols; i++ {
col := mat.Col(nil, i, m)
data[i] = floats.Sum(col)
}
output = mat.NewDense(1, numCols, data)
case 1:
data := make([]float64, numRows)
for i := 0; i < numRows; i++ {
row := mat.Row(nil, i, m)
data[i] = floats.Sum(row)
}
output = mat.NewDense(numRows, 1, data)
default:
return nil, errors.New("invalid axis, must be 0 or 1")
}
return output, nil
}
實現前向傳播進行預測
在訓練完我們的神經網路之後,我們希望使用它進行預測。為此,我們只需要將一些給定的鳶尾花特徵值輸入到網路中進行前向傳播,用來生成輸出。
有點像反向傳播邏輯,不同之處在於,這裡我們將返回生成的輸出:
// predict makes a prediction based on a trained
// neural network.
func (nn *neuralNet) predict(x *mat.Dense) (*mat.Dense, error) {
// Check to make sure that our neuralNet value
// represents a trained model.
if nn.wHidden == nil || nn.wOut == nil {
return nil, errors.New("the supplied weights are empty")
}
if nn.bHidden == nil || nn.bOut == nil {
return nil, errors.New("the supplied biases are empty")
}
// Define the output of the neural network.
output := new(mat.Dense)
// Complete the feed forward process.
hiddenLayerInput := new(mat.Dense)
hiddenLayerInput.Mul(x, nn.wHidden)
addBHidden := func(_, col int, v float64) float64 { return v + nn.bHidden.At(0, col) }
hiddenLayerInput.Apply(addBHidden, hiddenLayerInput)
hiddenLayerActivations := new(mat.Dense)
applySigmoid := func(_, _ int, v float64) float64 { return sigmoid(v) }
hiddenLayerActivations.Apply(applySigmoid, hiddenLayerInput)
outputLayerInput := new(mat.Dense)
outputLayerInput.Mul(hiddenLayerActivations, nn.wOut)
addBOut := func(_, col int, v float64) float64 { return v + nn.bOut.At(0, col) }
outputLayerInput.Apply(addBOut, outputLayerInput)
output.Apply(applySigmoid, outputLayerInput)
return output, nil
}
準備特徵和期望資料
下面我們需要準備鳶尾花的特徵和期望資料,可以在加州大學官網下載:https://archive.ics.uci.edu/ml/datasets/iris
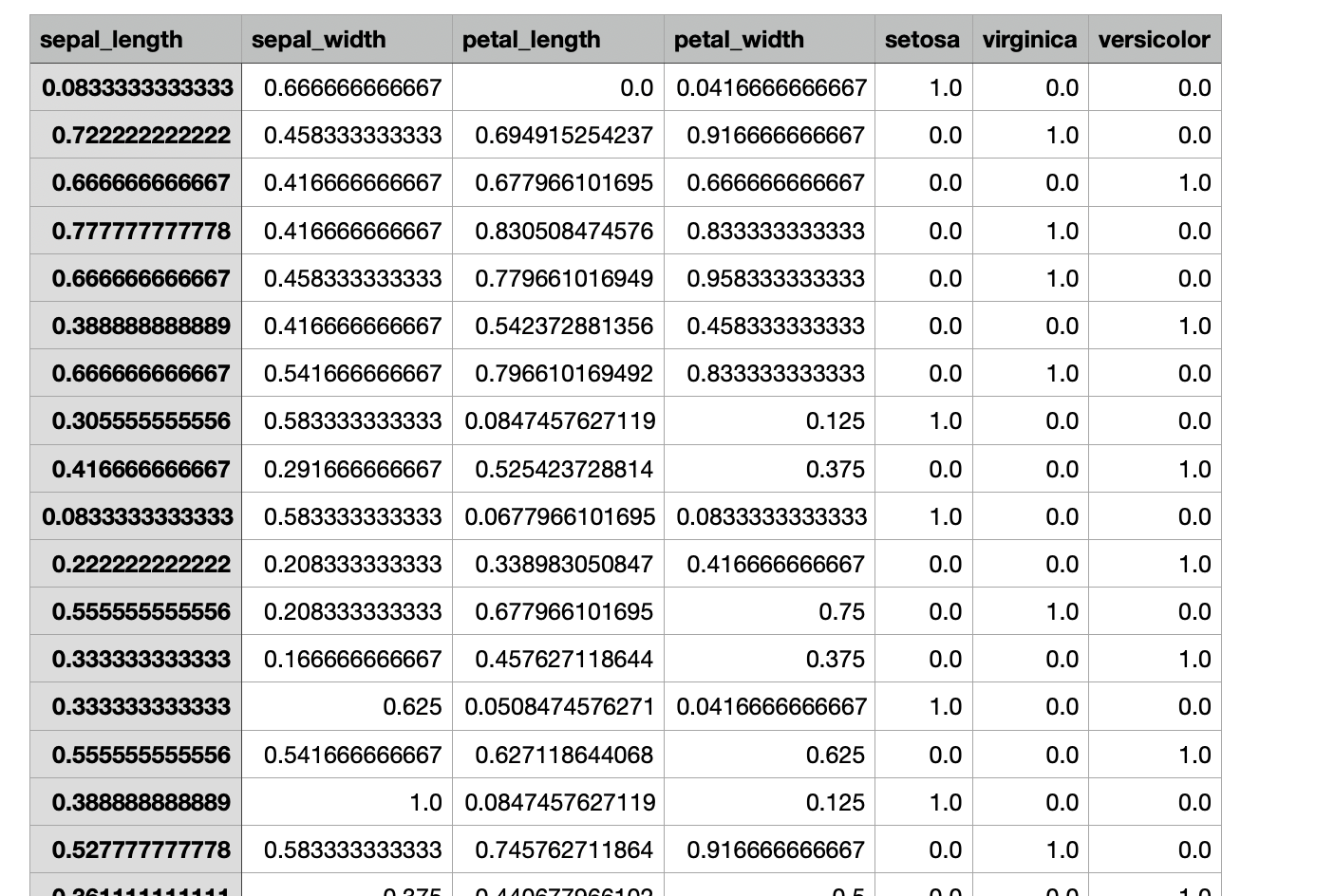
這裡包含花瓣和花蕊的具體資料,以及這些樣本所對應的花的種類,分別對應上文提到的山鳶尾(Iris Setosa)、維吉尼亞鳶尾(Iris Virginica)和 變色鳶尾(Iris Versicolour),注意鳶尾花種類順序分先後,分別對應上表中的資料。
開始訓練
訓練之前,需要安裝基於Golang的浮點庫:
go get gonum.org/v1/gonum/floats
安裝後之後,編寫指令碼:
package main
import (
"encoding/csv"
"errors"
"fmt"
"log"
"math"
"math/rand"
"os"
"strconv"
"time"
"gonum.org/v1/gonum/floats"
"gonum.org/v1/gonum/mat"
)
// neuralNet contains all of the information
// that defines a trained neural network.
type neuralNet struct {
config neuralNetConfig
wHidden *mat.Dense
bHidden *mat.Dense
wOut *mat.Dense
bOut *mat.Dense
}
// neuralNetConfig defines our neural network
// architecture and learning parameters.
type neuralNetConfig struct {
inputNeurons int
outputNeurons int
hiddenNeurons int
numEpochs int
learningRate float64
}
func main() {
// Form the training matrices.
inputs, labels := makeInputsAndLabels("data/train.csv")
// Define our network architecture and learning parameters.
config := neuralNetConfig{
inputNeurons: 4,
outputNeurons: 3,
hiddenNeurons: 3,
numEpochs: 5000,
learningRate: 0.3,
}
// Train the neural network.
network := newNetwork(config)
if err := network.train(inputs, labels); err != nil {
log.Fatal(err)
}
// Form the testing matrices.
testInputs, testLabels := makeInputsAndLabels("data/test.csv")
// Make the predictions using the trained model.
predictions, err := network.predict(testInputs)
if err != nil {
log.Fatal(err)
}
// Calculate the accuracy of our model.
var truePosNeg int
numPreds, _ := predictions.Dims()
for i := 0; i < numPreds; i++ {
// Get the label.
labelRow := mat.Row(nil, i, testLabels)
var prediction int
for idx, label := range labelRow {
if label == 1.0 {
prediction = idx
break
}
}
// Accumulate the true positive/negative count.
if predictions.At(i, prediction) == floats.Max(mat.Row(nil, i, predictions)) {
truePosNeg++
}
}
// Calculate the accuracy (subset accuracy).
accuracy := float64(truePosNeg) / float64(numPreds)
// Output the Accuracy value to standard out.
fmt.Printf("\nAccuracy = %0.2f\n\n", accuracy)
}
// NewNetwork initializes a new neural network.
func newNetwork(config neuralNetConfig) *neuralNet {
return &neuralNet{config: config}
}
// train trains a neural network using backpropagation.
func (nn *neuralNet) train(x, y *mat.Dense) error {
// Initialize biases/weights.
randSource := rand.NewSource(time.Now().UnixNano())
randGen := rand.New(randSource)
wHidden := mat.NewDense(nn.config.inputNeurons, nn.config.hiddenNeurons, nil)
bHidden := mat.NewDense(1, nn.config.hiddenNeurons, nil)
wOut := mat.NewDense(nn.config.hiddenNeurons, nn.config.outputNeurons, nil)
bOut := mat.NewDense(1, nn.config.outputNeurons, nil)
wHiddenRaw := wHidden.RawMatrix().Data
bHiddenRaw := bHidden.RawMatrix().Data
wOutRaw := wOut.RawMatrix().Data
bOutRaw := bOut.RawMatrix().Data
for _, param := range [][]float64{
wHiddenRaw,
bHiddenRaw,
wOutRaw,
bOutRaw,
} {
for i := range param {
param[i] = randGen.Float64()
}
}
// Define the output of the neural network.
output := new(mat.Dense)
// Use backpropagation to adjust the weights and biases.
if err := nn.backpropagate(x, y, wHidden, bHidden, wOut, bOut, output); err != nil {
return err
}
// Define our trained neural network.
nn.wHidden = wHidden
nn.bHidden = bHidden
nn.wOut = wOut
nn.bOut = bOut
return nil
}
// backpropagate completes the backpropagation method.
func (nn *neuralNet) backpropagate(x, y, wHidden, bHidden, wOut, bOut, output *mat.Dense) error {
// Loop over the number of epochs utilizing
// backpropagation to train our model.
for i := 0; i < nn.config.numEpochs; i++ {
// Complete the feed forward process.
hiddenLayerInput := new(mat.Dense)
hiddenLayerInput.Mul(x, wHidden)
addBHidden := func(_, col int, v float64) float64 { return v + bHidden.At(0, col) }
hiddenLayerInput.Apply(addBHidden, hiddenLayerInput)
hiddenLayerActivations := new(mat.Dense)
applySigmoid := func(_, _ int, v float64) float64 { return sigmoid(v) }
hiddenLayerActivations.Apply(applySigmoid, hiddenLayerInput)
outputLayerInput := new(mat.Dense)
outputLayerInput.Mul(hiddenLayerActivations, wOut)
addBOut := func(_, col int, v float64) float64 { return v + bOut.At(0, col) }
outputLayerInput.Apply(addBOut, outputLayerInput)
output.Apply(applySigmoid, outputLayerInput)
// Complete the backpropagation.
networkError := new(mat.Dense)
networkError.Sub(y, output)
slopeOutputLayer := new(mat.Dense)
applySigmoidPrime := func(_, _ int, v float64) float64 { return sigmoidPrime(v) }
slopeOutputLayer.Apply(applySigmoidPrime, output)
slopeHiddenLayer := new(mat.Dense)
slopeHiddenLayer.Apply(applySigmoidPrime, hiddenLayerActivations)
dOutput := new(mat.Dense)
dOutput.MulElem(networkError, slopeOutputLayer)
errorAtHiddenLayer := new(mat.Dense)
errorAtHiddenLayer.Mul(dOutput, wOut.T())
dHiddenLayer := new(mat.Dense)
dHiddenLayer.MulElem(errorAtHiddenLayer, slopeHiddenLayer)
// Adjust the parameters.
wOutAdj := new(mat.Dense)
wOutAdj.Mul(hiddenLayerActivations.T(), dOutput)
wOutAdj.Scale(nn.config.learningRate, wOutAdj)
wOut.Add(wOut, wOutAdj)
bOutAdj, err := sumAlongAxis(0, dOutput)
if err != nil {
return err
}
bOutAdj.Scale(nn.config.learningRate, bOutAdj)
bOut.Add(bOut, bOutAdj)
wHiddenAdj := new(mat.Dense)
wHiddenAdj.Mul(x.T(), dHiddenLayer)
wHiddenAdj.Scale(nn.config.learningRate, wHiddenAdj)
wHidden.Add(wHidden, wHiddenAdj)
bHiddenAdj, err := sumAlongAxis(0, dHiddenLayer)
if err != nil {
return err
}
bHiddenAdj.Scale(nn.config.learningRate, bHiddenAdj)
bHidden.Add(bHidden, bHiddenAdj)
}
return nil
}
// predict makes a prediction based on a trained
// neural network.
func (nn *neuralNet) predict(x *mat.Dense) (*mat.Dense, error) {
// Check to make sure that our neuralNet value
// represents a trained model.
if nn.wHidden == nil || nn.wOut == nil {
return nil, errors.New("the supplied weights are empty")
}
if nn.bHidden == nil || nn.bOut == nil {
return nil, errors.New("the supplied biases are empty")
}
// Define the output of the neural network.
output := new(mat.Dense)
// Complete the feed forward process.
hiddenLayerInput := new(mat.Dense)
hiddenLayerInput.Mul(x, nn.wHidden)
addBHidden := func(_, col int, v float64) float64 { return v + nn.bHidden.At(0, col) }
hiddenLayerInput.Apply(addBHidden, hiddenLayerInput)
hiddenLayerActivations := new(mat.Dense)
applySigmoid := func(_, _ int, v float64) float64 { return sigmoid(v) }
hiddenLayerActivations.Apply(applySigmoid, hiddenLayerInput)
outputLayerInput := new(mat.Dense)
outputLayerInput.Mul(hiddenLayerActivations, nn.wOut)
addBOut := func(_, col int, v float64) float64 { return v + nn.bOut.At(0, col) }
outputLayerInput.Apply(addBOut, outputLayerInput)
output.Apply(applySigmoid, outputLayerInput)
return output, nil
}
// sigmoid implements the sigmoid function
// for use in activation functions.
func sigmoid(x float64) float64 {
return 1.0 / (1.0 + math.Exp(-x))
}
// sigmoidPrime implements the derivative
// of the sigmoid function for backpropagation.
func sigmoidPrime(x float64) float64 {
return sigmoid(x) * (1.0 - sigmoid(x))
}
// sumAlongAxis sums a matrix along a
// particular dimension, preserving the
// other dimension.
func sumAlongAxis(axis int, m *mat.Dense) (*mat.Dense, error) {
numRows, numCols := m.Dims()
var output *mat.Dense
switch axis {
case 0:
data := make([]float64, numCols)
for i := 0; i < numCols; i++ {
col := mat.Col(nil, i, m)
data[i] = floats.Sum(col)
}
output = mat.NewDense(1, numCols, data)
case 1:
data := make([]float64, numRows)
for i := 0; i < numRows; i++ {
row := mat.Row(nil, i, m)
data[i] = floats.Sum(row)
}
output = mat.NewDense(numRows, 1, data)
default:
return nil, errors.New("invalid axis, must be 0 or 1")
}
return output, nil
}
func makeInputsAndLabels(fileName string) (*mat.Dense, *mat.Dense) {
// Open the dataset file.
f, err := os.Open(fileName)
if err != nil {
log.Fatal(err)
}
defer f.Close()
// Create a new CSV reader reading from the opened file.
reader := csv.NewReader(f)
reader.FieldsPerRecord = 7
// Read in all of the CSV records
rawCSVData, err := reader.ReadAll()
if err != nil {
log.Fatal(err)
}
// inputsData and labelsData will hold all the
// float values that will eventually be
// used to form matrices.
inputsData := make([]float64, 4*len(rawCSVData))
labelsData := make([]float64, 3*len(rawCSVData))
// Will track the current index of matrix values.
var inputsIndex int
var labelsIndex int
// Sequentially move the rows into a slice of floats.
for idx, record := range rawCSVData {
// Skip the header row.
if idx == 0 {
continue
}
// Loop over the float columns.
for i, val := range record {
// Convert the value to a float.
parsedVal, err := strconv.ParseFloat(val, 64)
if err != nil {
log.Fatal(err)
}
// Add to the labelsData if relevant.
if i == 4 || i == 5 || i == 6 {
labelsData[labelsIndex] = parsedVal
labelsIndex++
continue
}
// Add the float value to the slice of floats.
inputsData[inputsIndex] = parsedVal
inputsIndex++
}
}
inputs := mat.NewDense(len(rawCSVData), 4, inputsData)
labels := mat.NewDense(len(rawCSVData), 3, labelsData)
return inputs, labels
}
程式碼最後將測試集資料匯入,並且開始進行預測:
// Form the testing matrices.
testInputs, testLabels := makeInputsAndLabels("data/test.csv")
fmt.Println(testLabels)
// Make the predictions using the trained model.
predictions, err := network.predict(testInputs)
if err != nil {
log.Fatal(err)
}
// Calculate the accuracy of our model.
var truePosNeg int
numPreds, _ := predictions.Dims()
for i := 0; i < numPreds; i++ {
// Get the label.
labelRow := mat.Row(nil, i, testLabels)
var prediction int
for idx, label := range labelRow {
if label == 1.0 {
prediction = idx
break
}
}
// Accumulate the true positive/negative count.
if predictions.At(i, prediction) == floats.Max(mat.Row(nil, i, predictions)) {
truePosNeg++
}
}
// Calculate the accuracy (subset accuracy).
accuracy := float64(truePosNeg) / float64(numPreds)
// Output the Accuracy value to standard out.
fmt.Printf("\nAccuracy = %0.2f\n\n", accuracy)
程式輸出:
&{{31 3 [0 1 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 1 1 0 0 1 0 0 1 0 0 0 1 0 0 0 1 0 0 1 1 0 0 0 0 1 0 0 1 0 0 1 0 0 1 0 1 0 0 0 1 1 0 0 1 0 0 0 1 0 1 0 0 0 0 1 0 0 1 1 0 0 1 0 0 0 1 0 0 0 1 0 0 1 0 0 0] 3} 31 3}
Accuracy = 0.97
可以看到,一共31個測試樣本,只錯了3次,成功率達到了97%。
當然,就算是自己實現的小型神經網路,預測結果正確率也不可能達到100%,因為機器學習也是基於概率學範疇的學科。
為什麼使用Golang?
事實上,大部分人都存在這樣一個刻板影響:機器學習必須要用Python來實現。就像前文所提到的,機器學習和Python語言並不存在因果關係,我們使用Golang同樣可以實現神經網路,同樣可以完成機器學習的流程,程式語言,僅僅是實現的工具而已。
但不能否認的是,Python當前在人工智慧領域的很多細分方向都有比較廣泛的應用,比如自然語言處理、計算機視覺和機器學習等領域,但是並不意味著人工智慧研發一定離不開Python語言,實際上很多其他程式語言也完全可以替代Python,比如Java、C++、Golang等等。
機器學習相關業務之所以大量使用Python,是因為Python有著極其豐富的三方庫進行支援,能夠讓研發人員把更多的精力放在演演算法設計和演演算法訓練等方面,說白了,就是不用重複造輪子,提高研發團隊整體產出的效率,比如面對基於Python的Pytorch和Tensorflow這兩個顛撲不破的深度學習巨石重鎮,Golang就得敗下陣來,沒有任何優勢可言。
所以,單以人工智慧生態圈的繁榮程度而論,Golang還及不上Python。
結語
至此,我們就使用Golang完成了一個小型神經網路的實現,並且解決了一個真實存在的分類問題。那麼,走完了整個流程,我們應該對基於神經網路架構的機器學習過程有了一個大概的瞭解,那就是機器學習只能解決可以被解決的問題,有經驗或者相關知識儲備的人類通過肉眼也能識別鳶尾花的種類,機器學習只是幫我們提高了識別效率而已,所以,如果還有人在你面前吹噓他能夠用機器學習來預測A股價格賺大錢,那麼,他可能對機器學習存在誤解,或者可能對A股市場存在誤解,或者就是個純騙子,三者必居其一。