分類演演算法之k-近鄰

k-近鄰演演算法採用測量不同特徵值之間的距離來進行分類

優點：精度高、對異常值不敏感、無資料輸入假定

缺點：計算複雜度高、空間複雜度高

使用資料範圍：數值型和標稱型

一個例子弄懂k-近鄰

電影可以按照題材分類，每個題材又是如何定義的呢？那麼假如兩種型別的電影，動作片和愛情片。動作片有哪些公共的特徵？那麼愛情片又存在哪些明顯的差別呢？我們發現動作片中打鬥鏡頭的次數較多，而愛情片中接吻鏡頭相對更多。當然動作片中也有一些接吻鏡頭，愛情片中也會有一些打鬥鏡頭。所以不能單純通過是否存在打鬥鏡頭或者接吻鏡頭來判斷影片的類別。那麼現在我們有6部影片已經明確了類別，也有打鬥鏡頭和接吻鏡頭的次數，還有一部電影型別未知。

電影名稱	打鬥鏡頭	接吻鏡頭	電影型別
California Man	3	104	愛情片
He's not Really into dues	2	100	愛情片
Beautiful Woman	1	81	愛情片
Kevin Longblade	101	10	動作片
Robo Slayer 3000	99	5	動作片
Amped II	98	2	動作片
?	18	90	未知

那麼我們使用K-近鄰演演算法來分類愛情片和動作片：存在一個樣本資料集合，也叫訓練樣本集，樣本個數M個，知道每一個資料特徵與類別對應關係，然後存在未知型別資料集合1個，那麼我們要選擇一個測試樣本資料中與訓練樣本中M個的距離，排序過後選出最近的K個，這個取值一般不大於20個。選擇K個最相近資料中次數最多的分類。那麼我們根據這個原則去判斷未知電影的分類

電影名稱	與未知電影的距離
California Man	20.5
He's not Really into dues	18.7
Beautiful Woman	19.2
Kevin Longblade	115.3
Robo Slayer 3000	117.4
Amped II	118.9

我們假設K為3，那麼排名前三個電影的型別都是愛情片，所以我們判定這個未知電影也是一個愛情片。那麼計算距離是怎樣計算的呢？

歐氏距離 那麼對於兩個向量點a1和a2之間的距離,可以通過該公式表示：

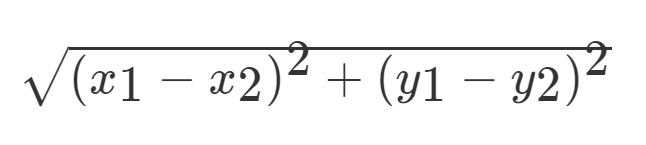
如果說輸入變數有四個特徵，例如（1，3，5，2）和（7，6，9，4）之間的距離計算為：

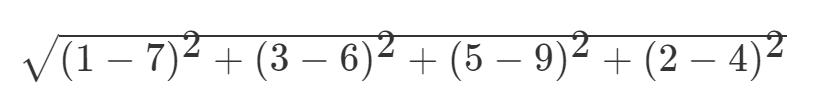
sklearn.neighbors

sklearn.neighbors提供監督的基於鄰居的學習方法的功能，sklearn.neighbors.KNeighborsClassifier是一個最近鄰居分類器。那麼KNeighborsClassifier是一個類，我們看一下範例化時候的引數

class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=1, **kwargs)**
  """
  :param n_neighbors：int，可選（預設= 5），k_neighbors查詢預設使用的鄰居數

  :param algorithm：{'auto'，'ball_tree'，'kd_tree'，'brute'}，可選用於計算最近鄰居的演演算法：'ball_tree'將會使用 BallTree，'kd_tree'將使用 KDTree，「野獸」將使用強力搜尋。'auto'將嘗試根據傳遞給fit方法的值來決定最合適的演演算法。

  :param n_jobs：int，可選（預設= 1),用於鄰居搜尋的並行作業數。如果-1，則將作業數設定為CPU核心數。不影響fit方法。

  """
import numpy as np
from sklearn.neighbors import KNeighborsClassifier

neigh = KNeighborsClassifier(n_neighbors=3)

Method

fit(X, y)

使用X作為訓練資料擬合模型，y作為X的類別值。X，y為陣列或者矩陣

X = np.array([[1,1],[1,1.1],[0,0],[0,0.1]])
y = np.array([1,1,0,0])
neigh.fit(X,y)

kneighbors(X=None, n_neighbors=None, return_distance=True)

找到指定點集X的n_neighbors個鄰居，return_distance為False的話，不返回距離

neigh.kneighbors(np.array([[1.1,1.1]]),return_distance= False)

neigh.kneighbors(np.array([[1.1,1.1]]),return_distance= False,an_neighbors=2)

predict(X)

預測提供的資料的類標籤

neigh.predict(np.array([[0.1,0.1],[1.1,1.1]]))

predict_proba(X)

返回測試資料X屬於某一類別的概率估計

neigh.predict_proba(np.array([[1.1,1.1]]))

K-鄰近演演算法鳶尾花資料集案例

In [ ]:

from sklearn.datasets import load_iris  # 匯入鳶尾花資料集
from sklearn.preprocessing import StandardScaler # 匯入特徵工程標準化
from sklearn.neighbors import KNeighborsClassifier # 匯入K鄰近模型
from sklearn.model_selection import train_test_split# 匯入劃分訓練集測試集方法
import pandas as pd

In [ ]:

iris = load_iris()  # 範例化鳶尾花資料集
df = pd.concat([pd.DataFrame(iris.data), pd.DataFrame(iris.target)],axis=1)
df

Out[ ]:

	0	1	2	3	0
0	5.1	3.5	1.4	0.2	0
1	4.9	3.0	1.4	0.2	0
2	4.7	3.2	1.3	0.2	0
3	4.6	3.1	1.5	0.2	0
4	5.0	3.6	1.4	0.2	0
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	2
146	6.3	2.5	5.0	1.9	2
147	6.5	3.0	5.2	2.0	2
148	6.2	3.4	5.4	2.3	2
149	5.9	3.0	5.1	1.8	2

150 rows × 5 columns

In [ ]:

# 劃分測試集和訓練集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.25)

In [ ]:

# 資料標準化
# 範例化標準化類，傳入訓練集資料計方差標準
std = StandardScaler().fit(x_train)
#範例化訓練集特徵值
x_train = std.transform(x_train)
#範例化測試集特徵值
x_test = std.transform(x_test)

In [ ]:

# K鄰近預測，K值為10
knn = KNeighborsClassifier(n_neighbors=10)
# 擬合k-nearest neighbors分類器
knn.fit(x_train,y_train)
# 檢視預測樣本的目標值
y_predict = knn.predict(x_test)
y_predict

Out[ ]:

array([0, 1, 0, 0, 1, 0, 2, 1, 2, 0, 1, 1, 0, 0, 0, 2, 0, 2, 1, 0, 2, 2,
       0, 2, 2, 2, 1, 2, 1, 0, 1, 0, 0, 0, 1, 2, 1, 1])

In [ ]:

#檢視預測準確度
score = knn.score(x_test,y_test)
score

Out[ ]:

0.9473684210526315