論文資訊

論文標題：PCL: Proxy-based Contrastive Learning for Domain Generalization
論文作者：
論文來源：
論文地址：download 
論文程式碼：download
參照次數：

1 前言

　　域泛化是指從一組不同的源域中訓練一個模型，可以直接推廣到不可見的目標域的問題。一個很有前途的解決方案是對比學習，它試圖通過利用來自不同領域的樣本到樣本對之間豐富的語意關係來學習領域不變表示。一種簡單的方法是將來自不同域的正樣本對拉得更近，同時將其他負樣本對推得更遠。

　　在本文中，我們發現直接應用基於對比的方法（如有監督的對比學習）在領域泛化中是無效的。本文認為，由於不同域之間的顯著分佈差距，對準正樣本到樣本對往往會阻礙模型的泛化。為了解決這個問題，提出了一種新的基於代理的對比學習方法，它用代理到樣本關係代替了原始的樣本-樣本關係，顯著緩解了正對齊問題。

2 方法

　　整體框架

　　　　

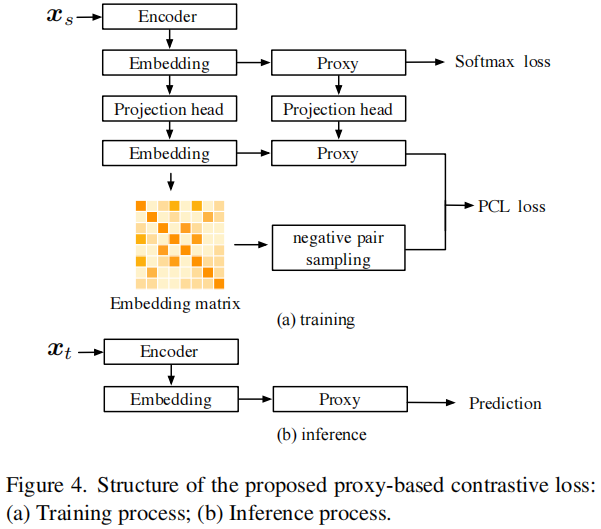
2.1 啟發

　　現有對比學習的對比損失大多考慮正對和負對，本文受到 [ 61 ] 損失函數的啟發，它只考慮正樣本之間的關係，假設 $x_i$、$x_j$ 是從同一類的不同源域進行取樣。設 $z=F_{\theta}(\boldsymbol{x})$ 是由特徵提取器 $F_{\theta}$ 提取的特徵，我們有： 

　　　　$\mathcal{L}_{\mathrm{pos}}=\frac{1}{\alpha} \log \left(1+\sum \exp \left(-\boldsymbol{z}_{i}^{\top} \boldsymbol{z}_{j} \cdot \alpha\right)\right)  \quad\quad\quad(1)$

　　實驗：是否使用 包含正對之間對比的 $\text{instance} - \text{instance}$ 之間的對比學習？

　　　　

　　結果：單純使用交叉熵損失比 交叉熵損失 +  正對之間的對齊 效果還好，所以跨域之間的正對對齊是有害的。

2.2 問題定義

　　多源域適應；

　　特徵提取器：$F_{\theta}: X \rightarrow Z$

　　分類器：$G_{\psi}: \mathcal{Z} \rightarrow \mathbb{R}^{C}$

2.3 交叉熵回顧

　　交叉熵損失函數：

　　　　$\mathcal{L}_{\mathrm{CE}}=-\log \frac{\exp \left(\boldsymbol{w}_{c}^{\top} \boldsymbol{z}_{i}\right)}{\exp \left(\boldsymbol{w}_{c}^{\top} \boldsymbol{z}_{i}\right)+\sum_{j=1}^{C-1} \exp \left(\boldsymbol{w}_{j}^{\top} \boldsymbol{z}_{i}\right)}  \quad\quad\quad(2)$

　　其中，$\boldsymbol{w}_{c}$ 代表目標域的某一類中心；

　　$\text{Softmax CE}$ 損失只考慮了代理到樣本的關係，而忽略了豐富的語意樣本與樣本之間的關係。

2.4 對比損失回顧

　　對比損失函數：

　　　　$\mathcal{L}_{\mathrm{CL}}=-\log \frac{\exp \left(\boldsymbol{z}_{i}^{\top} \boldsymbol{z}_{+} \cdot \alpha\right)}{\exp \left(\boldsymbol{z}_{i}^{\top} \boldsymbol{z}_{+} \cdot \alpha\right)+\sum \exp \left(\boldsymbol{z}_{i}^{\top} \boldsymbol{z}_{-} \cdot \alpha\right)}$

　　基於對比的損失考慮了豐富的樣本與樣本之間的關係。其關鍵思想是學習一個距離，將 $\text{positive pairs}$ 拉近，將 $\text{negative pairs}$ 推遠。

2.5 困難樣本挖掘

　　公式：

　　　　$\begin{aligned}\mathcal{L}_{\mathrm{CL}} & =\lim _{\alpha \rightarrow \infty} \frac{1}{\alpha}-\log \left(\frac{\exp \left(\alpha \cdot s_{p}\right)}{\exp \left(\alpha \cdot s_{p}\right)+\sum_{j=1}^{N-1} \exp \left(\alpha \cdot s_{n}^{j}\right)}\right) \\& =\lim _{\alpha \rightarrow \infty} \frac{1}{\alpha} \log \left(1+\sum_{j=1}^{N-1} \exp \left(\alpha\left(s_{n}^{j}-s_{p}\right)\right)\right) \\& =\max \left[s_{n}^{j}-s_{p}\right]_{+} .\end{aligned}$

　　理解：由於域之間的域差異很大，簡單的拉近正對之間的距離，拉遠負對之間的距離是不合適的，這是由於往往存在某些難學的樣本，使得模型總是識別錯誤。

2.6 基於代理的對比學習

　　$\text{Softmax}$ 損失 在學習類代理方面是有效的，能夠快速、安全地收斂，但不考慮樣本與樣本之間的關係。基於對比損失利用了豐富的 樣本-樣本 關係，但在優化密集的 樣本-樣本 關係方面訓練複雜性高。

　　　　$\mathcal{L}_{\mathrm{PCL}}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{\exp \left(\boldsymbol{w}_{c}^{\top} \boldsymbol{z}_{i} \cdot \alpha\right)}{Z}$

　　基於代理的對比損失：

　　　　$\mathcal{L}_{\mathrm{PCL}}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{\exp \left(\boldsymbol{w}_{c}^{\top} \boldsymbol{z}_{i} \cdot \alpha\right)}{Z}$

　　其中，

　　　　$Z=\exp \left(\boldsymbol{w}_{c}^{\top} \boldsymbol{z}_{i} \cdot \alpha\right)+\sum_{k=1}^{C-1} \exp \left(\boldsymbol{w}_{k}^{\top} \boldsymbol{z}_{j} \cdot \alpha\right)+\sum_{j=1, j \neq i}^{K} \exp \left(\boldsymbol{z}_{i}^{\top} \boldsymbol{z}_{j} \cdot \alpha\right)$

　　Note：$N$ 代表的是 $\text{batch_size}$ 的大小，$K$ 代表的是 $x_i$ 負樣本的數量。

2.7 施加投影頭的基於代理的對比學習

　　公式：

　　　　$\mathcal{L}_{\mathrm{PCL}-\mathrm{in}}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{\exp \left(\boldsymbol{v}_{c}^{\top} \boldsymbol{e}_{i}\right)}{E}$

　　其中，

　　　　$E=\exp \left(\boldsymbol{v}_{c}^{\top} \boldsymbol{e}_{i}\right)+\sum_{k=1}^{C-1} \exp \left(\boldsymbol{v}_{k}^{\top} \boldsymbol{e}_{j}\right)+\sum_{j=1, j \neq i}^{B} \exp \left(\boldsymbol{e}_{i}^{\top} \boldsymbol{e}_{j}\right)$

2.8 訓練

　　訓練目標：

　　　　$\mathcal{L}_{\text {final }}=\mathcal{L}_{\mathrm{CE}}+\lambda \cdot \mathcal{L}_{\text {PCL-in }}$

3 實驗結果

正對齊實驗的細節

　　

消融實驗

　　

超引數實驗

　　

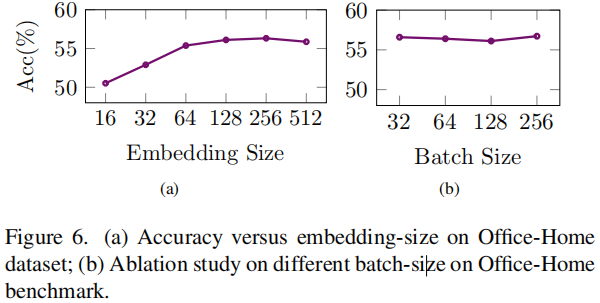
困難樣本分析

　　

 

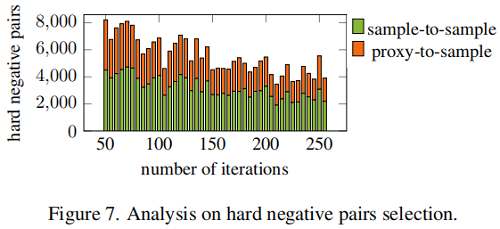
4 總結

　　略