「學習筆記」二分圖
「學習筆記」二分圖
點選檢視目錄
知識點
定義及判定
定義:存在一種方案把點分為兩個集合,使得同一個集合內的點沒有連邊的圖。
比如這張圖(by OI-Wiki):

判定:沒有奇環。
考慮染色法,左邊集合的點染成 \(1\),左邊集合的點染成 \(0\)。如果存在奇環則會有一個點不知道染成什麼顏色,因此不是二分圖。如果不存在奇環,所有點都會正常染色,分為兩個點集,因此是二分圖。
二分圖最大匹配
給定一個二分圖,分為左右兩部分,各部分之間的點沒有邊連線,要求選出一些邊,使得這些邊沒有公共頂點,且邊的數量最大。
有一個方法是轉換成網路流用 Dinic 演演算法解決,Link等寫完網路流學習筆記再掛連結。
本文主要講解增廣路演演算法(\(\text{Augmenting Path Algorithm}\))。
幾個定義:
- 匹配邊/非匹配邊:當前選上/沒選上的番。
- 交錯路:匹配邊與非匹配邊相間的一條路。
- 增廣路:以非匹配邊開頭和結束的一條交錯路。
演演算法過程用一個例子說明:
這是初始圖:
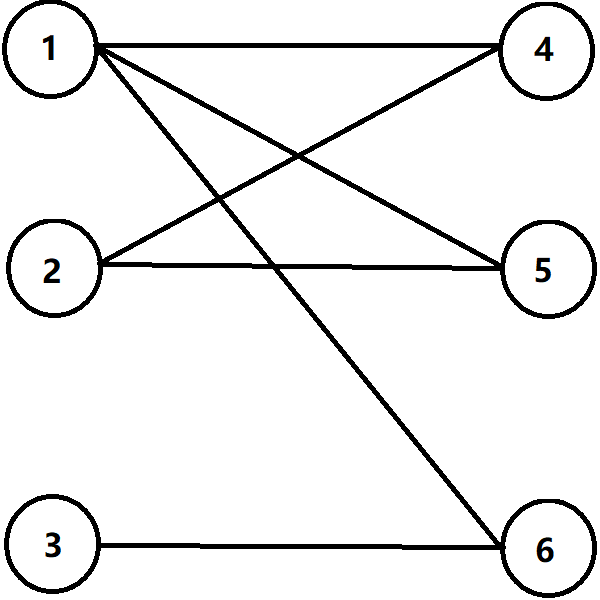
\(1\) 匹配了一個點 \(4\):
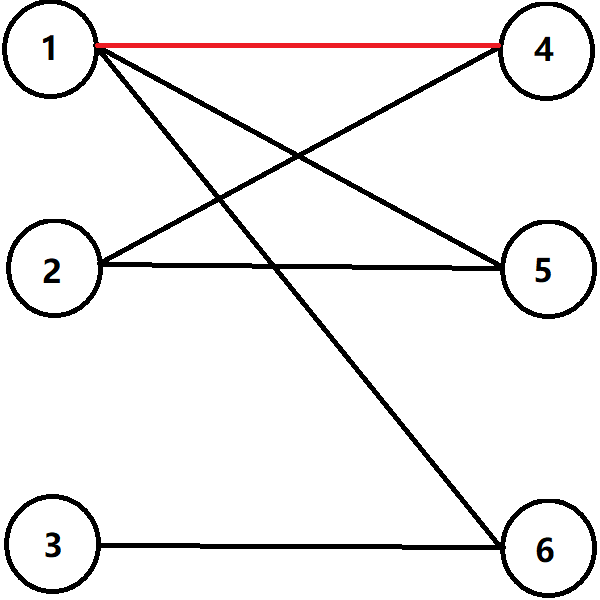
\(2\) 嘗試匹配 \(4\),但失敗了。
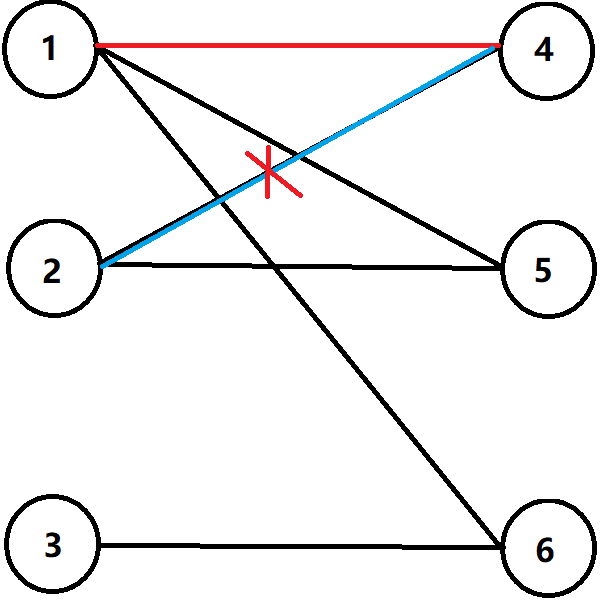
於是從 \(2\) 出發走一個增廣路。

將路上的匹配邊變為非匹配邊,非匹配邊變為匹配邊,這樣匹配數就會加一。

\(3\) 嘗試匹配 \(6\),但失敗了。
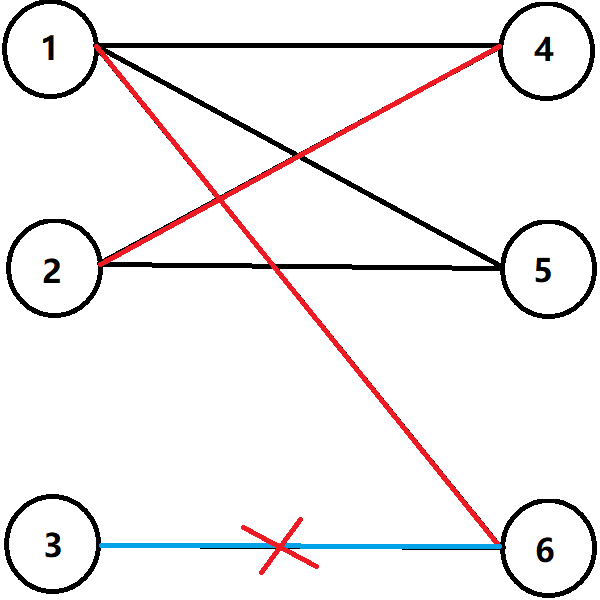
於是從 \(3\) 出發走一個增廣路。
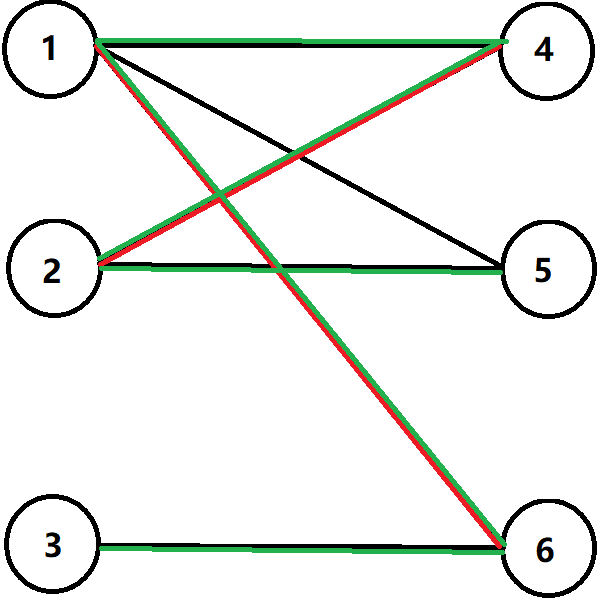
將路上的匹配邊變為非匹配邊,非匹配邊變為匹配邊,匹配數就會加一。
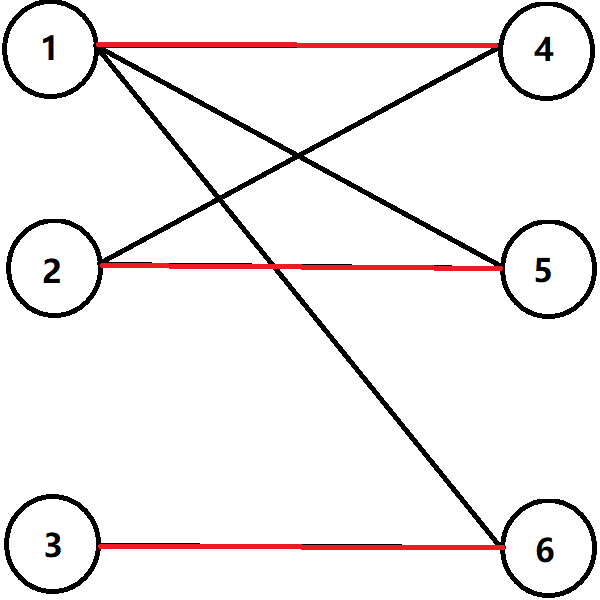
然後就匹配完成了,最大匹配值為 \(3\)。
程式碼:
ll n, jl[N], p[N], ans;
std::vector <ll> tu[N];
bool AugmentationPath (ll u) {
far (v, tu[u]) {
if (jl[v]) continue;
jl[v] = 1;
if (!p[v] || AugmentationPath (p[v])){
p[v] = u;
return true;
}
}
return false;
}
inline void Solve () {
_for (i, 1, n) {
memset (jl, 0, sizeof (jl));
ans += AugmentationPath (i);
}
return;
}
二分圖最小點覆蓋
最小點覆蓋:選最少的點,滿足每條邊至少有一個端點被選。
König 定理:二分圖中,最小點覆蓋 = 最大匹配。
證明
例圖:
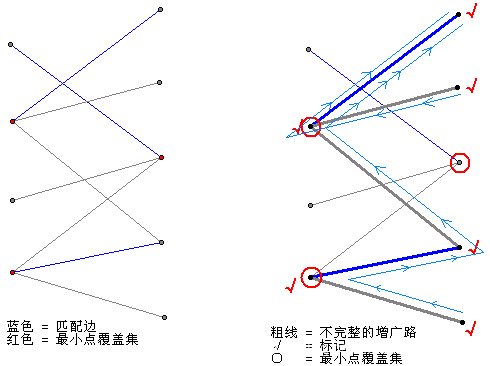
(圖是搬過來的,我也不知道為什麼他從右邊開始跑)
首先對一個二分圖跑完最大匹配,然後考慮構造一個點集:
從右邊未匹配點出發,盡力走交錯路,在經過的點上打標記。這條交錯路一定是由一條非匹配邊開頭,匹配邊結尾的交錯路,否則就不是最大匹配了。
選左邊的標記點和右邊的未標記點構成一個點集,這個點集就是一個最小點覆蓋,其大小等於最大匹配。
為什麼這個點集就是最小點覆蓋?思考以下三個問題。
這個點集為什麼是一個點覆蓋?
不難發現當一條邊左邊點沒被標記,右端點被標記的時候才不會被選。
- 當這條邊是一條匹配邊時,因為走交錯路上的匹配邊的時候就是從左邊走到右邊的,所以左邊點一定會先被標記,然後走到右邊才會標記右端點。
- 當這條邊不是一條匹配邊時,因為走交錯路上的非匹配邊的時候就是從右邊走到左邊的,所以右端點被標記後,一定會走到左邊並標記左端點。
因此這種邊是不存在的,所以不會存在任何一條邊不被選,因此這是一個點覆蓋。
其大小為什麼等於最大匹配?
對這個點覆蓋內的每個點進行分析:
- 如果這個點是左邊的標記點,它一定是在交錯路上因為有一條向右的匹配邊而被走到從而標記的。
- 如果這個點是右邊的無標記點,它一定因為有一條向左的匹配邊才不會被當做起點走交錯路而被標記。
每個點都覆蓋到了一條匹配邊,兩個點不會覆蓋同一條匹配邊,一條匹配邊必定會被覆蓋。因此這個點覆蓋內的點與最大匹配內的點一一對應,數量相等。
這個點集為什麼就是一個最小點覆蓋?
設最大匹配數為 \(k\)。
兩個點不會覆蓋同一條匹配邊,一條匹配邊必定會被覆蓋。
因此,一個點覆蓋的數量不可能少於 \(k\) 個點。
我們已經構造出了大小為 \(k\) 的點覆蓋,因為大小不可能再少了,所以這個點集為什麼就是一個最小點覆蓋!
解決這三個問題後,就可以得出結論了:最小點覆蓋 = 最大匹配!
二分圖最大獨立集
最大獨立集:選最多的點,滿足兩兩之間沒有邊相連。
定義也可以變為:選最多的點,滿足每條邊至多有一個端點被選。
那不就是最小點覆蓋的補集嗎?
所以大小是最大匹配 - 最小點覆蓋。
例題
二分圖的題目基本都是將題意抽象成一個二分圖,然後直接跑板子,難點在於建模,所以我不放次要的程式碼了。
P7368 [USACO05NOV]Asteroids G
思路
建模為二分圖:把列當成左邊點集,行當成右邊點集,第 \(i\) 行第 \(j\) 列的點當做第 \(i\) 行和第 \(j\) 列所代表的點的連邊。
要求選的列數和行數最小,覆蓋所有點,建模為二分圖後其實就等價於最小點覆蓋了。
P2319 [HNOI2006]超級英雄
思路
建模為二分圖:把題當成左邊點集,「錦囊妙計」當成右邊點集,在每道題和其能夠使用的兩種「錦囊妙計」連邊。
然後跑一個最大匹配,注意當前必須匹配上才能進入下一題,所以匹配失敗時直接退出。
Way Selection
題意
小杉家族 \(r\) 個人正在一片空地上散步,突然,外星人來了…… 留給小杉家族脫逃的時間只有 \(t\) 秒,每個小杉都有一個跑的速度 \(v\)。總共有 \(a\) 個傳送點,小杉們必須在 \(t\) 秒內到達傳送點才能脫逃。另外一個小杉進入一個傳送點以後,該傳送點就會消失 現在請你安排一種方案,使脫逃的小杉儘可能的多。
\(0<a,r,t\le1000\)。
思路
建模為二分圖:把人當成左邊點集,傳送點當成右邊點集,當 \(\operatorname{dis}(人,傳送點)\le vt\) 時在兩者之間連邊。
文理分班
題意
jzyz 每年的文理分班的時候,每個班都會有一些同學分到其他班,還會進入一些其他班的同學進入這個班。
小 x 負責安排座位,為了照顧分班帶來的那種傷感情緒,小 x 制定了很人性化的座位安排計劃,具體計劃如下:
比如 A 和 B 都是本班學生且是好朋友,A 分到了其他班,而 C 則是外班進入這個班的,C 和 A 並不熟悉,而 C 和 B 關係很好,那麼小 x 為了照顧 A 和 C 的情緒,就會讓 B 坐在 A 的位置,C 坐在 B 的位置。
當然,實際情況可能很複雜,比如一個班裡的同學之間關係不一定好,外班進來的可能和本班很多人關係都很好。
現在告訴你,和小 x 所在班有關係的人一共有 \(n\) 個人,小 x 想知道有沒有一個合理的方案來滿足自己的座位安排計劃。
對於 \(100\%\) 的資料滿足 \(1\le n\le50,1\le T\le 20\)。
思路
首先把題意翻譯成人話:自己認識自己,如果 A 認識 B,A 就可以坐到 B 的位置上。
建模為二分圖:把原來班的同學(的座位)當成左邊點集,現在班裡的同學當成右邊點集,當兩者認識時在兩者之間連邊。
當最大匹配數等於現在班裡的同學數時,存在合法方案。
放置機器人
題意
Robert 是一位著名的工程師。一天他的老闆給了他一個任務。任務的背景如下:
給出一張由方塊組成的地圖。方塊有許多種:牆,草,和空地。老闆想讓 Robert 在地圖上放置儘可能多的機器人。每個機器人拿著一把鐳射槍,它可以同時向東西南北四個方向射擊。機器人必須一直呆在它開始時被放在的位置並且不斷地射擊。鐳射束當然可以經過空地或草地,但不能穿過牆。機器人只能被放在空地上。當然老闆不希望看到機器人相互攻擊。換句話說,兩個機器人不能被放在一條線上(豎直或水平),除非它們中間有一堵牆。
由於你是一位機智的程式設計師和 Robert 的好基友之一,他請你幫他解決這個問題。也就是說,給出地圖的描述,計算地圖上最多能放置的機器人數量。
\(1\le m,n\le50\)。
思路
與 Asteroids G 比較像,但是由於有「牆」擋著,左右點集內的點不應是整個列和行,而是能儘量延長的橫線/豎線。
貓和狗
題意
小 k 同學正在玩一個遊戲,在遊戲中他扮演了一個馬戲團的老闆,現在小 k 同學需要利用馬戲團中的A只貓和B只狗舉辦一次表演,表演之前他讓觀眾進行了投票,投票的類容是:我想看到第___號貓/狗的表演,不想看到第___號貓/狗的表演。注意到每個觀眾都是更喜歡貓或更喜歡狗,所以兩個空後面一定會被勾上不同的內容。喜歡貓的觀眾會在第一空後面選擇貓,第二空後面選擇狗;反之就會在第一空後面選擇狗,第二空後面選擇貓。對於每一個觀眾,只有當 TA 投票的內容都被滿足了(即 TA 想看到的動物出場表演,TA 不想看到的動物不參與表演)的時候,TA 才會來看錶演。當然啦,看錶演是要付門票錢的,作為馬戲團的老闆,小 k 自然是希望來的人越多越好了。他想找到一個安排動物表演的方案,使得來看錶演的觀眾儘量多。
對於 \(100\%\) 的資料,\(n,m\le300,k\le500\)。
思路
建模為二分圖:把喜歡貓的人當成左點集,喜歡狗的人當成右點集,當 A 喜歡的貓/狗和 B 不喜歡的貓/狗相同時在兩者之間連邊。
不難發現跑個最大獨立集即可。
本文來自部落格園,作者:Keven-He,轉載請註明原文連結:https://www.cnblogs.com/Keven-He/p/BipartiteGraph.html