甩出11張圖-讓我們來構想(實現)一個倒排索引
甩出11張圖-讓我們來構想(實現)一個倒排索引
倒排索引的簡介
在介紹倒排索引之前,先看看傳統b+tree索引是如何儲存資料的,每次新增資料的時候,b+tree就會往自身節點上新增上新增資料的key值,如果節點達到了分裂的條件,那麼還會將一個節點分裂成兩個節點。
想一個場景,如果對使用者的性別建立b+tree索引,性別只有男女之分,這樣存在b+tree裡是不是會存很多重複的key,如果使用者資料量很大,我們想篩選出性別是男性的使用者,是不是要遍歷大量的資料。
而這種選擇性不高的資料,用倒排索引來做就很合適,倒排索引在面對那麼多使用者資料的情況下,只會存兩個key值,分別是男女,然後key對應的value值就是使用者id的集合,能一下就找到特定性別的使用者。
那麼倒排索引究竟長什麼樣呢?
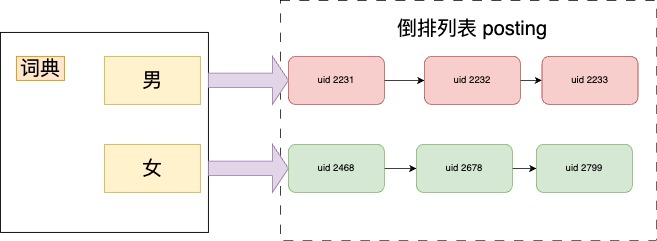
還是拿剛才那個場景舉例,用於查詢的key,構成倒排索引的詞典,而每個詞(key)都對應一個倒排列表,例如男性的key 對應的倒排列表 就包含了所有性別為男性的uid,而女性的key對應的則是另一個倒排列表,這個列表的uid全為女性。
那麼這樣的索引結構,我們究竟應該如何來實現呢。為了簡單起見,先來構建一個在記憶體上能用的倒排索引。
第一版 實現一個記憶體上的倒排索引
當我們在搜尋特定key對應的uid集合時,目的是找到容納uid集合的倒排列表,要找到倒排列表就必須找到與之對應的在詞典中的key值,所以我們先來看看如果你來實現一個詞典的結構,你會怎麼做。
如何實現詞典與倒排列表
詞典不外乎就是在一堆key值中找到某個特定的key值,我們可以直接採用hash結構嘛。直接將詞典中的每個key設定為hashmap的key,倒排列表設定為hashmap的value值,這樣不就行了嗎。
而關於倒排列表的實現是不是可以簡單的用一個集合來表示呢?這樣我在查男性或者女性的時候直接取出對應的集合,這樣不就實現了嗎?
當然,這是最簡單的版本,試想下其他場景,比如對使用者標籤建立倒排索引,一個使用者可以打上多個標籤,現在需要找出標籤同時為標籤A和標籤B的使用者,應該怎麼查詢。
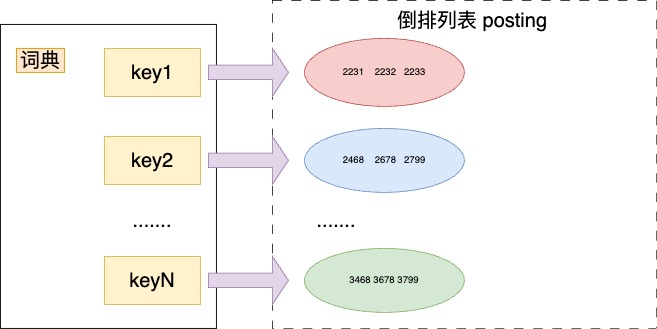
如圖,我們的倒排列表是集合,首先是不是可以找到標籤A和標籤B各自的倒排列表,集合無序但是可以遍歷,兩個for迴圈遍歷兩個倒排列表便可以求出其中即屬於標籤A又屬於標籤B的使用者了。假設兩個倒排列表的長度分別是m,n,那麼這樣的時間複雜度將會是O(m*n)。
能不能優化呢?可以。
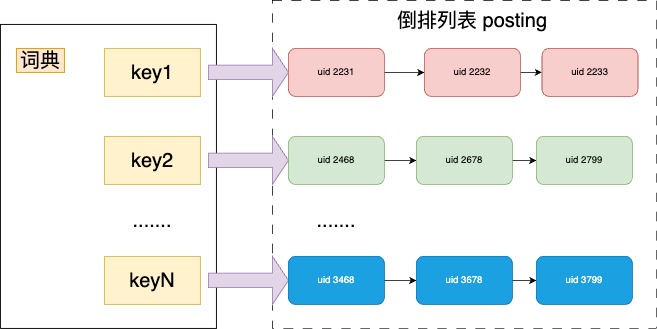
如上圖所示,如果將倒排列表設計成有序連結串列,那麼是不是可以用歸併排序的方式來遍歷兩個列表,這樣時間複雜度是O(m+n),連結串列查詢是快了,但是我們在往倒排列表中插入資料時,還得判斷資料是不是已經存在連結串列中,這樣就得遍歷整個連結串列,能不能優化這個過程呢?可以。
我們遍歷無非就是要找到這個資料是不是已經在倒排列表中了,如果在的話,我就不插入連結串列了。
那麼我們在最初插入連結串列時,除了將資料插入連結串列,還要再將資料插入到一個hash或者集合裡,等到後續再插入資料的時候,首先檢視map裡是否存在相同資料,相同則不進行接下來的插入工作,這樣是不是可以優化掉一部分連結串列的無效遍歷了。並且如果將倒排連結串列設計成雙向連結串列,在刪除的時候也可以先檢視hash結構查詢到需要刪除的節點,然後直接根據節點的前後指標,便可以在O(1)的時間複雜度完成刪除操作。 如圖:

好了,說了這麼多,關於記憶體上如何實現一個倒排索引,我覺得大家完全可以發揮自己的想象,在不同的場景下選擇不同的資料結構進行組裝,便能很輕鬆的實現一個基於記憶體的倒排索引。接下來,我們來看看,當倒排索引越來越大,大到記憶體放不下的時候,我們又該怎麼做。
第二版 實現一個磁碟上的倒排索引
既然是資料儲存,必然倒排索引會有記憶體不能完全放下的一天,這個時候,想想看,有沒有什麼辦法能在磁碟上很好的表示一個倒排索引結構?
如何實現詞典
記憶體上可以用hashmap來儲存詞典的key值,但是我們應該如何將詞典存在磁碟上呢,還記得之前提到過的b+tree(看了還不懂b+tree本質就來打我)嗎,它能很好的應對磁碟隨機讀的情況,正好可以拿來應用到詞典對key值的查詢上。
那麼如何來實現倒排列表呢?
既然存在磁碟上,那是不是也可以用b+tree儲存呢?其實也是可以的,不過這樣的設計會導致讀取倒排列表不會按檔案id遞增讀取,並且由於倒排列表不是遞增,那麼在多條件查詢時,將不能用多路歸併的方法進行檔案id的合併,提高了查詢時間複雜度。
既然這樣,那我們就將資料結構設計成順序的好了,還記得前面實現記憶體上的倒排列表時採用的什麼資料結構嗎,有序連結串列。那麼是不是可以直接將資料順序寫入到磁碟就行了,比如按檔案id是int型別且佔8個位元組計算,那麼每次讀取按8位元組的步長就可以讀取每一個檔案id了。我們將磁碟想像成一個超大容量的陣列。
我們的倒排索引將會變成這樣。

詞典中的key值指向key在磁碟上的開頭位置。
可以看出,如果按固定步長進行磁碟儲存,其實儲存的是一個有序陣列的結構.這樣可以很好利用磁碟順序讀寫的高效性特點。
但是這樣會面臨倒排索引更新的問題,因為在磁碟上有序儲存,如果要在這個倒排列表上新增一個檔案id,那麼要移動磁碟資料,這樣的代價顯然太大。
如果把磁碟上的資料結構變成一個有序連結串列呢,每次儲存時按有序連結串列的節點進行儲存,那麼每個節點除了要包含檔案id的8個位元組,還要再包含指向下一個節點的位置。這樣新增一個檔案id,是不是可以往倒排列表所在的磁碟空間末尾新增一個節點的空間,然後讓倒排節點的末尾節點指向新增的節點即可,不用移動磁碟資料。
這樣我們的倒排索引在磁碟上就會變成下面這張圖的樣子,各個倒排連結串列之間是通過指標關聯在了一起,而詞典的key指向的是連結串列頭部的元素在磁碟上的位置。
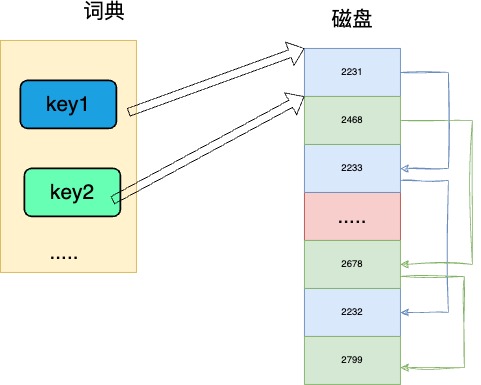
但是,又是一個但是,如果對這樣的倒排列表頻繁進行刪除和更新會怎麼樣,之前在講b+tree本質的時候,有說過由於節點的刪除和更新,b+tree相鄰父子節點之間只是位置相鄰,在磁碟空間上可能並不相鄰。
對於連結串列來說也是一樣,頻繁的插入和刪除就會導致順序的資料在磁碟上可能分佈在不同磁軌了,可以看到,同一個key的倒排列表在磁碟上並不相鄰, 在讀取倒排列表時,將會有過多的隨機讀產生,嚴重影響效能。
既然這樣,能不能借鑑下LSM對索引合併的思路(剖析LSM索引原理),對索引的更新採取合併的策略,而不是原地更新的方式,比如,在新增檔案時,會去構建增量的詞典和倒排索引,這一部分索引暫時不可見,只有等到這部分索引和歷史可見索引進行合併後,才會真正被搜尋到。
如圖所示,同一個顏色屬於同一個倒排列表。
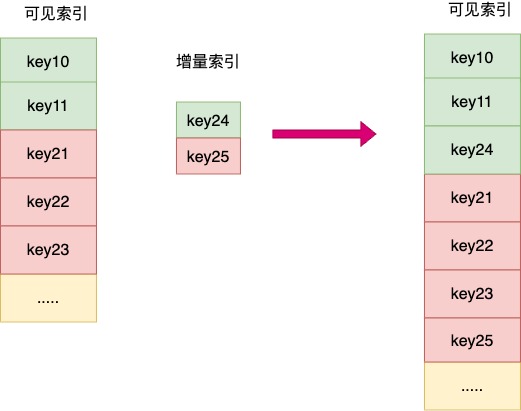
這樣雖然犧牲了一點立即可見性,但由於合併時是寫入到一個新的倒排檔案裡,將會是順序寫,同一個倒排連基本是在相同的磁軌上,這樣讀取倒排列表時便可以有很好的讀取效能。
採用索引合併的策略是不是就沒有其他問題呢?它同樣面臨索引合併的常見問題,一個小數量級的索引和大數量級的索引進行合併時,會產生很多無效合併。新的增量的倒排索引是比較少量的,而歷史的索引數量級是比較龐大的,每次由於新增的倒排索引需要合併就要去遍歷整個歷史的索引檔案顯然是划不來的。
一個比較簡單的解決辦法就是,直接將大的索引檔案拆分成很多個小段的索引檔案,我們將這些由大索引分割的小索引檔案叫做segment,每個segment是有它自己的詞典和倒排列表。
選擇合併索引的策略也是選擇大小相近的segment索引檔案進行合併,每個小的索引檔案裡有各自的詞典和倒排列表。這樣查詢的時候可能就麻煩點,需要查詢多個小的索引檔案,不過這樣的查詢完全可以採用多cpu同時並行查詢進行加速。如下圖所示,是將增量的倒排索引合併到存量索引的過程,合併時,只將segment2和segment3進行合併。
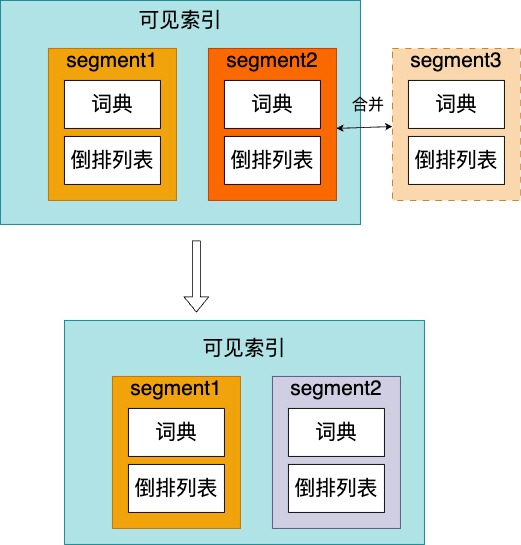
注意雖然將這種分割後的小詞典和它的倒排列表的組合稱作segment,但是segment在磁碟上並不一定是隻用一個檔案,我們完全可以對segment進行編號後,通過不同的字尾對不同型別的檔案進行取名。如圖所示:
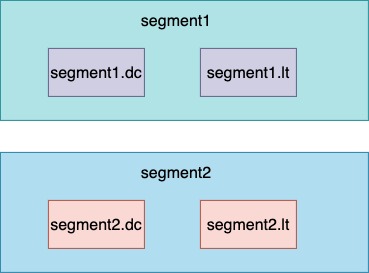
假設 檔案segment1.dc代表segment1的詞典,segment1.lt檔案代表segment1的倒排列表。.dc字尾表明這是一個詞典檔案,.lt字尾表明這是儲存一個倒排列表的檔案。
再回到起初 詞典是怎麼儲存在磁碟上的問題上,我們採用了b+tree結構,但是將索引分成多個小的索引檔案之後,我們要想查某個詞對應的倒排列表,是不是要每個小的索引檔案都要去用小索引檔案他們各自的b+tree詞典去查一遍存不存在這個詞呢?這樣即使是多cpu查詢,但是大量的隨機讀會把查詢瓶頸壓在磁碟上。
詞典存磁碟存取慢是因為詞典無法存在記憶體裡,詞典無法儲存在記憶體上的原因是詞典過於大了,所以我們得想辦法壓縮詞典的大小。
所以,有沒有什麼辦法能壓縮詞典的大小呢?
我將直接揭曉答案,採用字首樹的資料結構能很有效的將詞典的體積縮小到記憶體能夠容納的範圍。字首樹的節點包含了詞中的每個字母,並且表明了從根節點到此節點上的路徑是否構成了一個詞典中的詞。如圖:
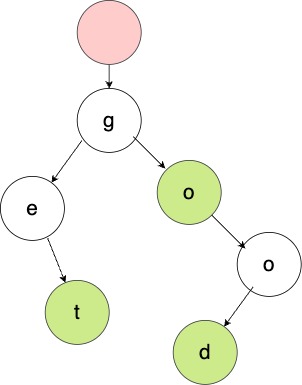
綠色的節點代表從根節點到該節點的路徑上存在一個詞,這顆字首樹能夠代表的字母為get,go,good。比如英文字母只有26個,這樣用字首樹組合形成的詞語儲存方式可以極大的省掉大量字首相同的詞的儲存空間。
這樣,每個小的索引檔案(segment)便可以將詞典對應的字首樹儲存到記憶體中了。這下我們來完成倒排索引最後的架構圖。
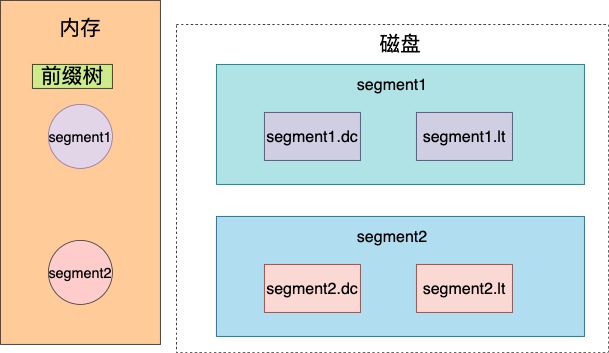
每一個segment索引檔案都有自己的字首樹結構在記憶體中。
整個倒排索引的查詢過程就變成了先查記憶體中的字首樹結構,找到特定的詞所在segment.dl詞典檔案的位置,我們實現詞典檔案的儲存採用b+tree的方式,然後通過查詢詞典檔案,再找到具體的倒排列表的位置,我們採用有序連結串列順序寫入倒排列表的方式讓詞典中屬於同一個詞的倒排列表中的元素儘量相鄰,提高倒排列表從磁碟讀取的效率。
至此,我們實現了一個基於磁碟的倒排索引,但優化遠遠沒有結束。例如,業界上在實現倒排列表時,為了極致的壓縮儲存空間,採用了一些壓縮方案例如Frame of ,並且為了提高聯合查詢效率,將倒排連結串列設計成跳錶,將倒排列表查詢結果快取起來等等。希望我的文章能拋磚引玉,引發大家更多的思考。
創作不易,如果覺得我的文章對你有幫助,關注一下,點個贊吧