緒論

我們在第一章引進複合過程時，採用了求值的代換模型定義了將過程應用於實參（arguments）的意義：

• 將一個複合過程應用於一些實參，也就意味著用實參替換過程體裡對應的形參（formal parameters）之後，求值這個過程體。

但正如我們在上一章部落格《SICP：賦值和區域性狀態（Python實現）》中所講的，一旦我們把賦值引入程式設計語言之後，這一定義就不再合適了。由於賦值的存在，變數已經不能再看作僅僅是某個值的名字，此時的變數必須以某種方式指定了一個「位置」（place），相應的值可以儲存再那裡。 在我們新求值模型裡，這種位置將維持在稱為環境的結構中。

一個環境就是幀（frame） 的一個序列，每個幀是包含著一些繫結（bindings） 的表格。這些約束將一些變數名字關聯於對應的值（在一個幀內，任何變數至多隻有一個繫結）。

每個幀還包含一個指標，指向這個幀的外圍環境（enclosing environment）。如果由於當前討論的目的，將相應的幀看做是全域性（global） 的，那麼它將沒有外圍環境。一個變數相對於某個特定環境的值，也就是在這一環境中，包含著該變數的第一個幀裡這個變數的繫結值。如果在幀序列中不存在這一變數的繫結，則稱這個變數在特定環境下是未繫結（unbound） 的。

下圖展示了一個簡單的環境結構。其中包含了三個幀，分別用Ⅰ、Ⅱ、Ⅲ標記。

在這個圖裡，A、B、C和D都是環境指標，其中C和D指向同一個環境。變數z和x在幀Ⅱ裡繫結，變數y和x在幀Ⅰ裡繫結。x在環境D裡的值是3，x相對於環境B的值也是3。後一種情況是因為我們先檢測幀序列中的第一個幀（幀Ⅲ），在這裡沒有找到x的繫結，因此繼續前進到外圍環境D並在幀Ⅰ裡找到了相應的繫結。另一方面，x在環境A中的值就是7，因為幀序列中第一個幀（幀Ⅱ）裡包含x與7的繫結。對於環境A，我們說在幀Ⅱ裡x與7的繫結遮蔽了幀1裡x與3的繫結(這裡可以聯想一下Python中區域性變數對全域性變數的遮蔽)。

環境對於求值是至關重要的，因為它確定了表示式求值的上下文（context）。實際上，我們完全可以說在一個程式設計語言裡的一個表示式本身沒有任何意義，因為即使像1+1這樣簡單的表示式，其解釋也要依賴於+是表示加法符號的上下文。這樣，在現在討論的求值模型中，我們將總說某個表示式相對於某個環境的求值。為了描述與直譯器的互動作用，我們將始終假定存在著一個全域性環境，它只包含著一個幀（沒有外圍環境），這個環境裡包含著所有關聯於基本過程的符號值。例如，我們說+是表示加法的符號，也就意味著符號+在全域性環境中被繫結到基本的加法過程。

3.2.1 求值規則

關於直譯器如何求值一個組合式的問題，其整體描述仍然與我們在1.1.3節第一次介紹時完全一樣。

在1.1.3節中的代換模型中，我們如果要對一個組合表示式求值，需要：
(1) 求值這一組合式裡的各個子表示式。
(2) 將運運算元（operator）子表示式的值應用於運算物件（operand）子表示式的值。

PS：賦值的存在給求值規則的步驟 (1) 引入了一個微妙問題，即以不同的順序對組合式中各個子表示式求值，它們就會產出不同的值（想想在C語言中被(++i)+(++i)支配的恐懼^[2]）。然而，這種順序應該看做是一個實現細節，我們永遠不要去寫依賴於特定順序的程式。比如，如果一個複雜的編譯器去做程式的優化，它完全可能改變其中各子表示式的求值順序。

現在我們要用求值的環境模型代替求值的代換模型，在這一模型中我們將會討論當定義一個複合過程以及當一個複合過程應用於實參究竟意味著什麼。

我們來看一個例子。考慮在全域性環境裡求值下面的過程定義：

def square(x):
    return x * x

下圖展示的是在全域性環境中求值這一def表示式而產生的環境結構：

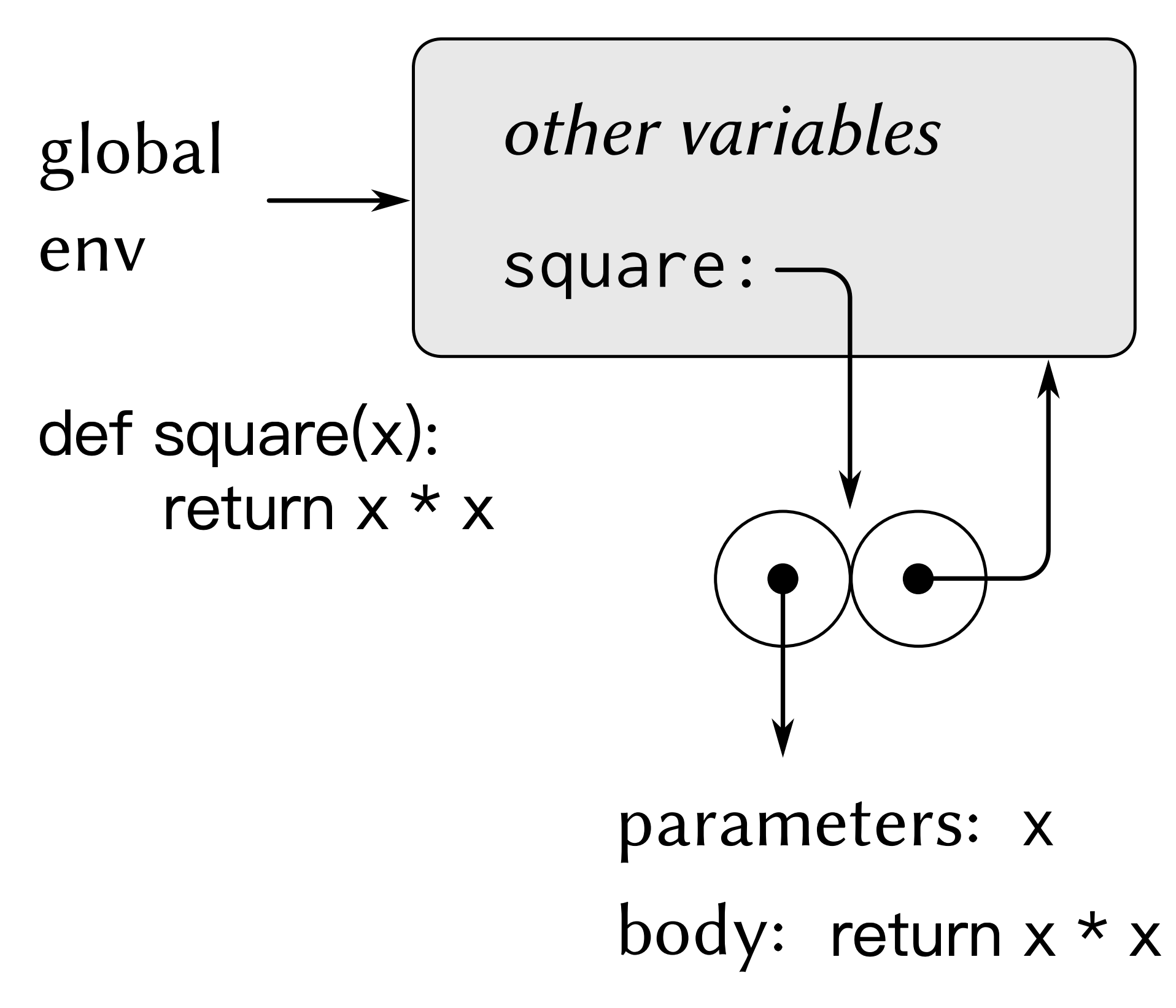
這裡的過程物件是一個序對（pair），其程式碼部分描述的是一個帶有形參x的過程，過程體是return x * x。過程物件的環境部分是一個指向全域性環境的指標（因為這個過程的定義是在全域性環境中求值的）。這個定義在全域性幀中加入了一個新系結，將上述過程物件繫結於符號square。一般而言，用def建立定義的方式（Python的話用=也可表示變數定義）就是將新的繫結加入到幀中。

這樣，過程物件建立的環境模型可總結定為：

• 對於一個給定環境求值一個過程的定義，將建立起一個過程物件，這個過程物件是一個序對，由該過程的正文和一個指向環境的指標組成，這一指標指向的就是建立這個過程物件時的環境。

接下來我們來描述過程物件的應用。環境模型說明，將一個過程物件應用於一組實參時，將會建立起一個新的環境，其中包含了將所有形參繫結到對應實參的一個幀。該幀的外圍環境就是建立該過程物件時的環境（在這個例子中即全域性環境），隨後就在這個新環境下求值該過程的體。

下面我們來演示這一規則的實施情況，下圖展示了在全域性環境裡對錶示式square(5)求值而建立起來的環境結構，其中square即上圖中生成的過程。這一過程應用的結果是建立了一個新環境E1。這個環境從一個幀開始，幀中包含著將這個過程的形參x約束到實參5。這個幀引出的指標說明這個幀的外圍環境就是全域性環境。現在我們要在E1裡求值過程的體return x * x。因為在E1裡x的值是5，所以求值結果是return 5 * 5，也就是return 25。

這樣，過程物件的應用的環境模型可總結為：

• 將一個過程物件應用於一集實參，將造出一個新幀，其中將過程的形參繫結到呼叫時的實參，而後在構造起的這一新環境的上下文中求值過程體。這個新幀的外圍環境就是建立該過程物件時的環境（這個例子中即全域性環境）。

PS：所謂定義一個符號(包括用def foo()定義過程或用foo = 1定義變數），也就是在當前環境frame裡建一個繫結，並賦予這個符號指定的值。而賦值運算=則會要求我們首先在環境中確定有關變數的繫結位置，然後再修改這個繫結，使之表示為這個新值。這也就是說，首先需要找到包括這個變數繫結的第一個幀，然後修改這個幀。如果該變數在環境中沒有繫結，賦值將報一個錯誤。當然由於Python語法的緣故，x = ...可同時表示變數定義和賦值，故此處注意例外。

此外，眾所周知，Python的基礎資料型別(如整形、字串等)是不可變（immutable）的，故對基礎資料型別而言，所謂賦值運算其實就等同於我們前面說的拿符號去繫結新的物件）。

3.2.2 簡單過程的應用

在1.1.5節裡介紹代換模型時，我們展示了在有下面過程的定義之後，組合式f(5)。怎樣求值得到135：

def square(x):
    return x * x

def sum_of_squares(x, y):
    return square(x) + square(y)

def f(a):
    return sum_of_squares(a + 1, a * 2)

print(f(5)) # 136

現在我們用環境模型來分析同一個範例，下圖中展示出在全域性環境裡對f、square和sum_of_squares的定義求值後建立起的三個過程物件，每個過程物件都由一些程式碼和一個指向全域性環境的指標組成。

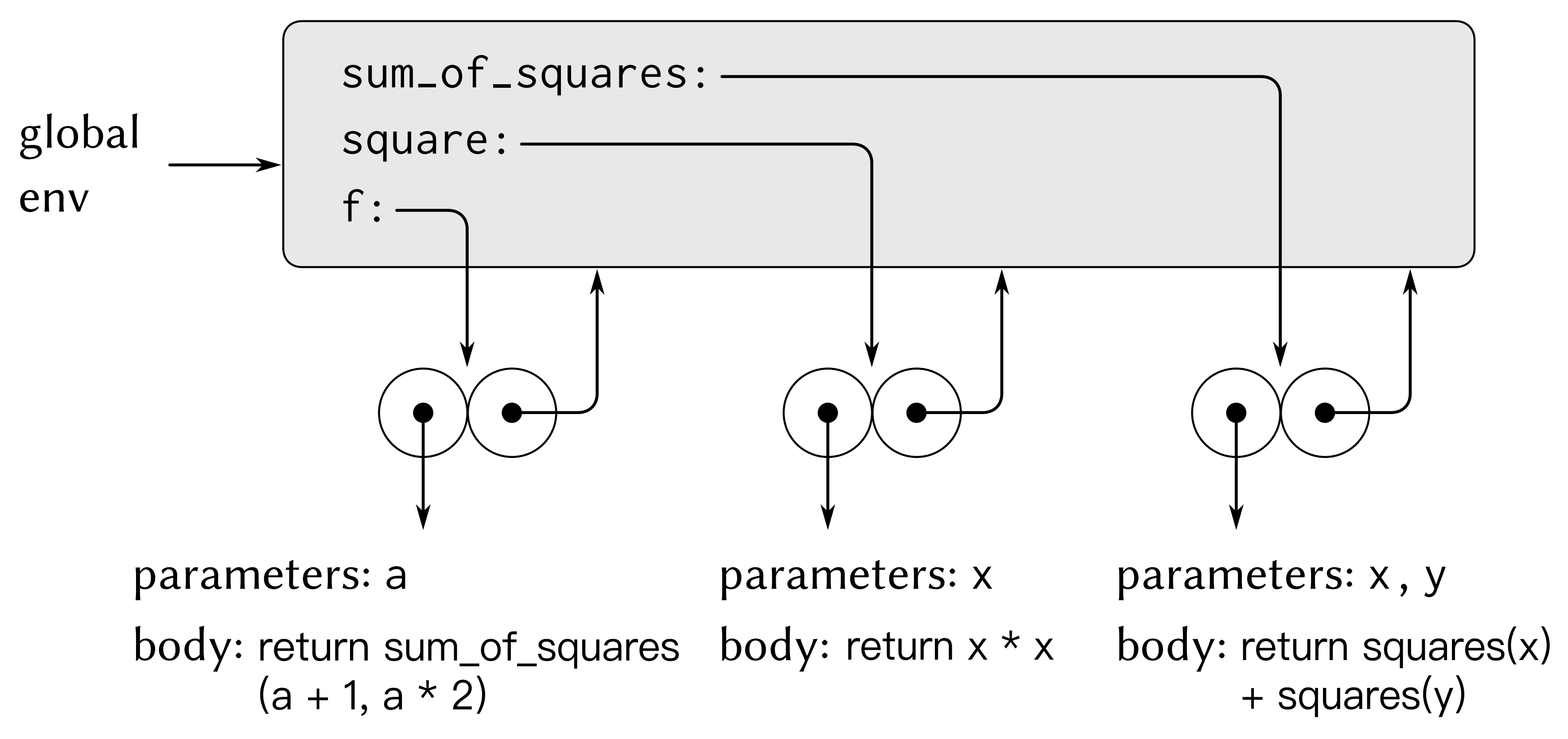
而在下圖中，我們看到的是對f(5)求值建立起的環境結構。

對於f的呼叫建立了一個新環境E1，它開始於一個幀，其中f的形參a被繫結到實參5。我們需要在E1裡求值f的體：

return sum_of_squares(a + 1, a * 2)

求值sum_of_squares這個組合式時，正如我們前面所說的，首先需要求值其中的子表示式。第一個子表示式sum_of_squares以一個過程物件為值（請注意看這個值是如何找到的：首先在E1的第一個幀裡找，這裡沒有包含sum_of_squares的繫結。而後進入有關的外圍環境，即全域性環境，並在那裡找到了建立過程物件時確立好的繫結）。對另外兩個子表示式的求值是應用兩個基本運運算元+和*，通過求職組合式a + 1和a * 2分別得到6和10。

現在需要把過程物件sum_of_squares應用於實參6和10，這時得到的是一個新環境E2，形式引數x和y在其中繫結與其對應的實際引數6和10，然後繼續在E2裡求值組合式square(x) + square(y)，以此類推。

這裡需要注意的是，對square的每個呼叫都會建立起一個包含著x的繫結的新環境，事實上這就是通過不同的幀去維護所有名字為x的區域性變數互不相同。還請注意，由square建立的每個幀都指向全域性環境，因為square過程物件需要從全域性環境中找到。

各個子表示式求值後返回得到的值，對square的兩個呼叫產生的值被sum_of_squares加起來，作為求值的結果返回。因為我們在這裡關心的是環境結構，因此將不仔細考察這些返回值在呼叫之間傳遞的問題，留到第5章討論（將會涉及到堆疊結構）。

3.2.3 將幀看作區域性狀態的儲存庫（repository）

現在可以從環境模型出發，看看怎樣用過程和賦值表示帶有區域性狀態的物件。作為一個例子，還是考慮取自3.1.1節的由呼叫下面過程建立的「提款處理器」：

def make_withdraw(balance):
    def withdraw(amount):
        nonlocal balance
        if balance > amount:
            balance = balance - amount
            return balance
        else:
            return "Insufficient funds"
    return withdraw

讓我們仔細看看下式的求值：

W1 = make_withdraw(100)

而後做：

print(W1(50)) # 50

下圖展示了在全域性環境裡定義make_withdraw過程的結果。這一求值產生出一個過程物件，其中包含著一個指向全域性環境的指標。

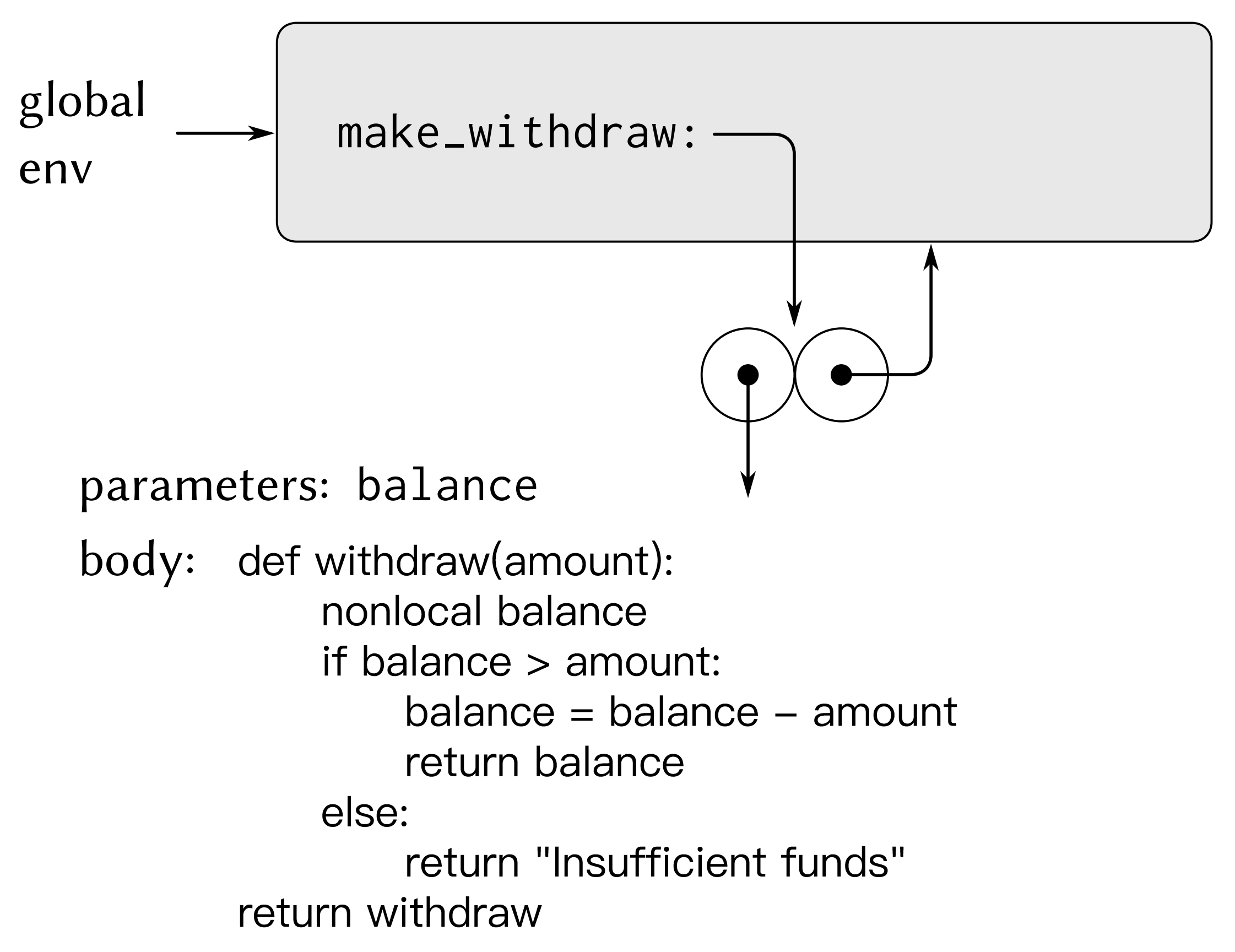
到目前為止，這個範例中還沒出現於前面看過的範例不同的東西，除了過程體中內建一個閉包函數withdraw之外。

計算中有趣的現象出現在將過程make_withdraw應用於一個實參的時候：

W1 = make_withdraw(100)

與往常一樣，我們在開始時設定了環境E1，其中將形參balance繫結到實參100。並接著在這一環境裡求值make_withdraw的體，也即內建閉包函數withdraw的定義。然後有趣之處來了，這一求值構造起一個新過程物件，其程式碼由這個閉包函數所描述，而它的環境就是E1。這樣做出過程物件被作為呼叫make_withdraw的返回值，在全域性環境裡繫結於符號W1，因為W1 = ...這個變數定義本身的求值是在全域性環境裡進行的。下圖顯示出這樣的結果得到的環境結構。

PS：上圖make_withdraw中之所以要加nonlocal，乃是在因為Python中想要修改外圍環境中的自由變數，必須要加nonlocal/global將其先繫結到內層環境，而Lisp則不需要人工繫結。

Python的作用域規則和SML、Lisp一樣，採用詞法作用域（lexical scope）^[3]規則。所謂詞法作用域規則，即在過程中遇到自由變數（不是形參也不是函數內部定義的區域性變數）時，要去參照外圍過程定義中所出現的繫結，也即去本過程定義的環境中查詢（這裡的順序即是著名的LEGB規則^[4]：Local scopes -> Enclosing -> Global -> Built-in）；與之相反的是動態作用域，即在過程中遇到自由變數時，去函數呼叫時的環境中查詢。 欲瞭解更多詞法作用域和動態作用域的知識，可參見知乎問題[5]。

現在讓我們來分析將W1應用於一個引數時所發生的情況：

print(W1(50)) # 50

此時首先要構造出一個幀，W1的形參amount在其中繫結到實參50。需要注意的最關鍵的一點是，這個幀的外圍環境並不是全域性環境，而是環境E1，因為它才是由過程物件W1所指定的外圍環境。現在我們需要在這個新環境中求值下面的過程體：

    nonlocal balance
    if balance > amount:
        balance = balance - amount
        return balance
    else:
        return "Insufficient funds"

這樣做得到的環境結構如下圖所示。在被求值的表示式裡參照了amount和balance，其中amount在環境裡的第一個幀中就能找到，而balance則沿著外圍環境指標向前在E1裡找到。

在執行賦值運算=時，位於E1裡balance的繫結就被修改了。對W1的呼叫完成時，balance是50，而包含著這個balance的幀仍由過程物件W1指著。繫結amount的那個幀（即執行修改balance的程式碼的那個幀）現在已經無關緊要了，因為構造它的過程已經結束。在下次W1被呼叫時，這一過程又會構造另一個幀，其中建立起amount的一個新系結，這個幀的外圍環境還是E1。根據上面的分析，我們可以看到E1怎樣起著儲存過程物件的區域性狀態變數的「位置」的作用。下圖展示的便是呼叫W1之後的情景。

現在來看我們通過再次呼叫make_withdraw，建立起第二個「提款」物件的情況：

W2 = make_withdraw(100)

這樣做產生出的環境結構如下圖所示。其中顯示了W2是另一個過程物件。通過呼叫make_withdraw為W2建立起的環境是E2，它包含了一個幀，其中包含著它自己對balance的區域性繫結。在另一方面，W1和W2擁有相同的程式碼，也就是在make_withdraw體內的那個閉包函數withdraw所確定的程式碼（這裡究竟W1和W2是共用計算機裡儲存的同一段物理程式碼，還是各自維持自己的一份拷貝，則完全是一種實現細節，我們在第4章實現的直譯器裡採用共用程式碼的方式）。這裡對W1呼叫參照的是儲存在E1裡的狀態變數balance，對W2的呼叫參照的是在E2裡的balance，故 W1和W2在行為上是完全獨立的物件。

3.2.4 內部定義

1.1.8節裡我們介紹了過程可以有內部定義的思想，這樣就引入了塊結構（block structure），就像下面計算平方根的過程裡的情況：

def sqrt(x):
    def is_good_enough(guess):
        return abs(guess**2 - x) < 0.001

    def improve(guess):
        return (guess + x/guess)/2

    def sqrt_iter(guess):
        if is_good_enough(guess):
            return guess
        else:
            return sqrt_iter(improve(guess))
        
    return  sqrt_iter(1.0)

print(sqrt(2)) # 1.4142156862745097

這也是一個詞法作用域的經典例子。現在我們可以利用上面的環境模型，去考察為什麼這些內部定義具有所需要的行為。下圖所示的是表示式sqrt(2)求值中的一個時刻，此時內部過程is_good_enough被第一次呼叫，其中的guess等於1.

注意這時的環境結構。sqrt是全域性環境裡的一個符號，它被繫結到一個過程物件，與之關聯的環境就是全域性環境。在sqrt被呼叫時，形成了一個新的環境E1，它將成為全域性環境的下屬。在E1中，引數x被繫結到2，而後在E1裡求值sqrt的體。由於sqrt體中的第一個表示式是：

def is_good_enough(guess):
    return abs(guess**2 - x) < 0.001

對這一表示式在環境E1裡求值並定義出過程is_good_enough。更準確地說，符號is_good_enough被加入到E1的第一個幀中，並被繫結於一個過程物件，其關聯的環境是E1（注意這裡過程物件和其符號不在全域性環境中繫結，這點和我們之前講的閉包有鮮明區別，在閉包中雖然閉包函數雖然有自己的外圍環境，但閉包函數物件和其符號卻仍然是在全域性環境中繫結的）。與此類似，improve和sqrt_iter也在E1裡定義為過程。為了簡潔起見，在上圖中只顯示了繫結於is_good_enough的過程物件。

在定義好各個區域性過程物件之後，表示式sqrt_iter(1.0)被求值，還是在環境E1裡。因此，呼叫在E1裡繫結於符號sqrt_iter的過程物件時，我們以1作為實參。然後這一呼叫建立了另一個環境E2，在其中sqrt_iter的形參guess被繫結到1。sqrt_iter轉而（在E2裡）以guess作為實參呼叫is_good_enough，這就建立了另一個環境E3。此時雖然sqrt_iter和is_good_enough都有名字為guess的形參，但它們是兩個不同的區域性變數，位於不同的幀中。與之相對地，E2和E3都以E1作為其外圍環境，這樣出現在sqrt_iter和is_good_enough體內部的符號x都將參照出現在E1裡x的繫結，也就是原來sqrt被呼叫時的那個x值。

這樣，環境模型已經解釋清楚了以前區域性過程定義作為程式化模組技術的兩個關鍵性質：

• 區域性過程的名字不會與它們外圍過程之外的名字互相干擾。這是因為這些區域性過程的名字都是在他們的外圍過程執行時所建立的幀裡繫結的，而不是在全域性環境中繫結的。

• 區域性過程只需要將它們外圍過程的形參作為自由變數，就可以存取外圍過程的實參。這是因為對於區域性過程體的求值所在的環境是它們外圍過程求值所在的環境的下屬。

參考

• [1] Abelson H, Sussman G J. Structure and interpretation of computer programs[M]. The MIT Press, 1996.

• [2] 知乎：i＝1，為什麼 (++i)+(++i)＝6？

• [3] Stackoverflow：Does Python scoping rule fits the definition of lexical scoping? [duplicate]

• [4] Real Python Tutorials: Python Scope & the LEGB Rule: Resolving Names in Your Code

• [5] 知乎：動態作用域和詞法域的區別是什麼？