演演算法總結--動態規劃
宣告(
疊甲):鄙人水平有限,本文為作者的學習總結,僅供參考。
1.動態規劃介紹
動態規劃,英文:Dynamic Programming,簡稱DP,如果某一問題有很多重疊子問題,使用動態規劃是最有效的。其中每一個狀態一定是由上一個狀態推匯出來,這是DP的一個重要標誌。
2.DP大法的使用
一般的來說,使用DP大法一般有以下幾個重要的步驟
【1】 確定 DP 陣列下標的含義
【2】 根據題意推匯出遞迴公式(狀態轉移方程)
【3】 初始化 DP 陣列,一般要進行邊界處理,有時也會通過擴大陣列的大小來避免邊界的處理
【4】 遍歷 DP 陣列,並進行對應的更新
3.舉些栗子
3.1 線性 DP —— 斐波那契數
題目如下:
題目描述
斐波那契數?(通常用 F(n) 表示)形成的序列稱為 斐波那契數列 。該數列由 0 和 1 開始,後面的每一項數位都是前面兩項數位的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
給定 n ,請計算 F(n) 。
根據題目描述顯然這個問題可以使用 DP 大法進行求解,且已給出了其狀態轉移方程 F(n) = F(n - 1) + F(n - 2),以及對應的邊界F(0) = 0,F(1)?= 1,於是我們就能夠順利寫出對應的程式碼
int fib(int n)
{
if(n == 0) return 0;
if(n == 1) return 1;
int dp_n = 0;
int dp_n_1 = 1;
int dp_n_2 = 0;
for(int i = 0;i < n-1;i++)
{
dp_n = dp_n_1 + dp_n_2;
dp_n_2 = dp_n_1;
dp_n_1 = dp_n;
}
return dp_n;
}
3.2 二維 DP —— 過河卒
題目描述
棋盤上 A 點有一個過河卒,需要走到目標 B 點。卒行走的規則:可以向下、或者向右。同時在棋盤上 C 點有一個對方的馬,該馬所在的點和所有跳躍一步可達的點稱為對方馬的控制點。因此稱之為「馬攔過河卒」。
棋盤用座標表示,A 點 (0, 0)、B 點 (n, m),同樣馬的位置座標是需要給出的。
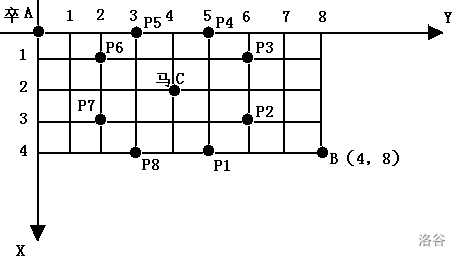
現在要求你計算出卒從 $A$ 點能夠到達 $B$ 點的路徑的條數,假設馬的位置是固定不動的,並不是卒走一步馬走一步。
該題可以說是不同路徑問題的變種,根據題目描述,我們可以設卒到(x,y)處的方案有dp[x][y]種,又卒只能向下、或者向右,故可以推出其狀態轉移方程為dp[x][y]=dp[x-1][y]+dp[x][y-1],接著是邊界與特殊點(馬的控制點)的處理,具體可以看程式碼的實現:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int m,n,x_m,y_m;
cin >> n >> m >> x_m >> y_m;
long long int dp[n+1][m+1];
for(int i = 0;i <= n;i++)
{
for(int j = 0;j <= m;j++)
{
int d_m = (i-x_m)*(i-x_m) + (j-y_m)*(j-y_m); // 卒到馬距離的平方
if(d_m == 5 || d_m == 0) dp[i][j] = 0;
else if(i == 0 && j == 0) dp[i][j] = 1; // 起點
else if(i == 0 && j != 0) dp[i][j] = dp[i][j-1]; // 上邊界
else if(j == 0 && i != 0) dp[i][j] = dp[i-1][j]; // 左邊界
else dp[i][j] = dp[i-1][j] + dp[i][j-1]; // 正常情況
}
}
cout << dp[n][m] << endl;
return 0;
}
3.2 四維 DP —— 方格取數
題目描述
設有 N 的方格圖(N<9),我們將其中的某些方格中填入正整數,而其他的方格中則放入數位 0。如下圖所示(見樣例):
A
0 0 0 0 0 0 0 0
0 0 13 0 0 6 0 0
0 0 0 0 7 0 0 0
0 0 0 14 0 0 0 0
0 21 0 0 0 4 0 0
0 0 15 0 0 0 0 0
0 14 0 0 0 0 0 0
0 0 0 0 0 0 0 0
B
某人從圖的左上角的 A 點出發,可以向下行走,也可以向右走,直到到達右下角的 B 點。在走過的路上,他可以取走方格中的數(取走後的方格中將變為數位 0)。
此人從 A 點到 B 點共走兩次,試找出 2 條這樣的路徑,使得取得的數之和為最大。
該題的難點在於有兩條路線同時進行,但是思考清楚後還是很簡單的,按照 DP 大法的步驟來
【1】 設兩條路徑分別到兩點 (i,j)與(k,l)時的最大的數為 DP[i][j][k][l]
【2】 根據觀察可以推得狀態轉移方程為 DP[i][j][k][l] = max(a,b), 其中 a,b 如下:
a = max(dp[i-1][j][k-1][l],dp[i-1][j][k][l-1])
b = max(dp[i][j-1][k-1][l],dp[i][j-1][k][l-1])
【3】 邊界的處理,在此我們可以多申明出一個都為 0 的第 0 行與第 0 列
程式碼實現如下:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int nums[10][10] = {0,};
int dp[10][10][10][10] = {0,};
int n = 0;
cin >> n;
while(1)
{
int x,y,a;
cin >> x >> y >>a;
if(x == 0 && y == 0 && a == 0) break;
nums[x][y] = a;
}
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= n;j++)
{
for(int k = 1;k <= n;k++)
{
for(int l = 1;l <= n;l++)
{
int a = max(dp[i-1][j][k-1][l],dp[i-1][j][k][l-1]);
int b = max(dp[i][j-1][k-1][l],dp[i][j-1][k][l-1]);
dp[i][j][k][l] = max(a,b) + nums[i][j] + nums[k][l];
if(i == k && j == l) dp[i][j][k][l] -= nums[i][j];
}
}
}
}
cout << dp[n][n][n][n];
return 0;
}
4.參考
本文到此結束,希望對您有所幫助。