刷爆 LeetCode 周賽 337,位掩碼/回溯/同餘/分桶/動態規劃·打家劫舍/貪心
本文已收錄到 AndroidFamily,技術和職場問題,請關注公眾號 [彭旭銳] 提問。
大家好,我是小彭。
上週末是 LeetCode 第 337 場周賽,你參加了嗎?這場周賽第三題有點放水,如果按照題目的資料量來說最多算 Easy 題,但如果按照動態規劃來做可以算 Hard 題。
小彭的技術交流群 02 群來了,公眾號回覆 「加群」 加入我們~
周賽概覽
2595. 奇偶位數(Easy)
- 題解一:模擬 $O(lgn)$
- 題解二:位掩碼 + bitCount $O(1)$
2596. 檢查騎士巡視方案(Medium)
- 題解一:模擬 $O(n^2)$
2597. 美麗子集的數目(Medium)
- 題解一:回溯 $O(2^n)$
- 題解二:同餘分組 + 動態規劃 / 打家劫舍 $O(nlgn)$
2598. 執行操作後的最大 MEX(Medium)
- 題解一:同餘分組 + 貪心 $O(n)$

2595. 奇偶位數(Easy)
題目地址
https://leetcode.cn/problems/number-of-even-and-odd-bits/
題目描述
給你一個 正 整數 n 。
用 even 表示在 n 的二進位制形式(下標從 0 開始)中值為 1 的偶數下標的個數。
用 odd 表示在 n 的二進位制形式(下標從 0 開始)中值為 1 的奇數下標的個數。
返回整數陣列 answer ,其中 answer = [even, odd] 。

題解一(模擬)
簡單模擬題。
寫法 1:列舉二進位制位
class Solution {
fun evenOddBit(n: Int): IntArray {
val ret = intArrayOf(0, 0)
for (index in 0..30) {
if (n and (1 shl index) != 0) {
ret[index % 2]++
}
}
return ret
}
}
複雜度分析:
- 時間複雜度:$O(U)$ 其中 $U$ 是整數二進位制位長度;
- 空間複雜度:$O(1)$ 僅使用常數級別空間。
寫法 2:不斷取最低位,然後右移 n,當 n 為 0 時跳出:
class Solution {
fun evenOddBit(n: Int): IntArray {
val ret = intArrayOf(0, 0)
var x = n
var index = 0
while (x != 0) {
ret[i] += x and 1 // 計數
x = x ushr 1 // 右移
i = i xor 1 // 0 -> 1 或 1 -> 0
}
return ret
}
}
複雜度分析:
- 時間複雜度:$O(lgn)$
- 空間複雜度:$O(1)$ 僅使用常數級別空間。
題解二(位掩碼 + bitCount)
使用二進位制掩碼 01010101 取出偶數下標,再使用 Integer.bitCount() 計算位 1 的個數:
class Solution {
fun evenOddBit(n: Int): IntArray {
val mask = 0b0101_0101_0101_0101_0101_0101_0101_0101
return intArrayOf(
Integer.bitCount(n and mask),
Integer.bitCount(n) - Integer.bitCount(n and mask)
)
}
}
複雜度分析:
- 時間複雜度:$O(1)$ Java Integer.bitCount() 庫函數的時間複雜度是 $O(1)$,如果按照常規實現是 $O(lgn)$;
- 空間複雜度:$O(1)$
2596. 檢查騎士巡視方案(Medium)
題目地址
https://leetcode.cn/problems/check-knight-tour-configuration/
題目描述
騎士在一張 n x n 的棋盤上巡視。在有效的巡視方案中,騎士會從棋盤的 左上角 出發,並且存取棋盤上的每個格子 恰好一次 。
給你一個 n x n 的整數矩陣 grid ,由範圍 [0, n * n - 1] 內的不同整陣列成,其中 grid[row][col] 表示單元格 (row, col) 是騎士存取的第 grid[row][col] 個單元格。騎士的行動是從下標 0 開始的。
如果 grid 表示了騎士的有效巡視方案,返回 true;否則返回 false。
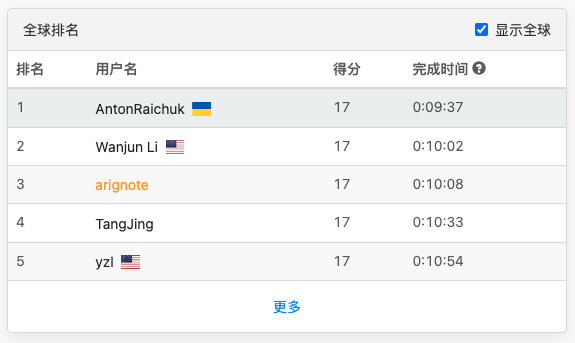
注意,騎士行動時可以垂直移動兩個格子且水平移動一個格子,或水平移動兩個格子且垂直移動一個格子。下圖展示了騎士從某個格子出發可能的八種行動路線。

題解(模擬)
二維簡單模擬題。
class Solution {
fun checkValidGrid(grid: Array<IntArray>): Boolean {
if (grid[0][0] != 0) return false
val directions = arrayOf(
intArrayOf(1, 2),
intArrayOf(2, 1),
intArrayOf(2, -1),
intArrayOf(1, -2),
intArrayOf(-1, -2),
intArrayOf(-2, -1),
intArrayOf(-2, 1),
intArrayOf(-1, 2)
)
val n = grid.size
var row = 0
var column = 0
var count = 1
outer@ while (count < n * n) {
for (direction in directions) {
val newRow = row + direction[0]
val newColumn = column + direction[1]
if (newRow < 0 || newRow >= n || newColumn < 0 || newColumn >= n) continue
if (count == grid[newRow][newColumn]) {
row = newRow
column = newColumn
count++
continue@outer
}
}
return false
}
return true
}
}
複雜度分析:
- 時間複雜度:$O(C·n^2)$ 其中 $C$ 是騎士的行走方向,$C$ 為常數 8;
- 空間複雜度:$O(1)$
2597. 美麗子集的數目(Medium)
題目地址
https://leetcode.cn/problems/the-number-of-beautiful-subsets/
題目描述
給你一個由正整陣列成的陣列 nums 和一個 正 整數 k 。
如果 nums 的子集中,任意兩個整數的絕對差均不等於 k ,則認為該子陣列是一個 美麗 子集。
返回陣列 nums 中 非空 且 美麗 的子集數目。
nums 的子集定義為:可以經由 nums 刪除某些元素(也可能不刪除)得到的一個陣列。只有在刪除元素時選擇的索引不同的情況下,兩個子集才會被視作是不同的子集。

預備知識
- 同餘性質:
如果 x % m == y % m,則稱 x 和 y 對模 m 同餘,即為 x ≡ (y mod m)
- 乘法定理:
如果某個任務有 n 個環節,每個環節分別有 ${m_1, m_2, m_3, …, m_n}$ 種方案,那麼完成任務的總方案數就是 $m_1m_2m3…m_n$。
題解一(暴力回溯)
由於題目的資料量非常小(陣列長度只有 20),所以可以直接使用暴力演演算法。
演演算法:列舉所有子集,並且增加約束條件:如果已經選擇過 x - k 或 x + k,則不能選擇 x。
class Solution {
private var ret = 0
fun beautifulSubsets(nums: IntArray, k: Int): Int {
subsets(nums, 0, k, IntArray(k + 1001 + k)/* 左右增加 k 避免陣列下標越界 */)
return ret - 1 // 題目排除空集
}
// 列舉子集
private fun subsets(nums: IntArray, start: Int, k: Int, cnts: IntArray) {
// 記錄子集數
ret++
if (start == nums.size) return
for (index in start until nums.size) {
val x = nums[index] + k // 偏移 k
if (cnts[x - k] != 0 || cnts[x + k] != 0) continue // 不允許選擇
// 選擇
cnts[x]++
// 遞迴
subsets(nums, index + 1, k, cnts)
// 回溯
cnts[x]--
}
}
}
複雜度分析:
- 時間複雜度:$O(2^n)$ 其中 $n$ 為 $nums$ 陣列長度,每個位置有選和不選兩種狀態,每個狀態的時間複雜度是 $O(1)$,因此整體時間複雜度是 $O(2^n)$;
- 空間複雜度:$O(C)$ 陣列空間。
題解二(同餘分組 + 動態規劃 / 打家劫舍)
這道題如果不使用暴力解法,難度應該算 Hard。
根據同餘性質,如果 x 和 y 對模 k 同餘,那麼 x 和 y 有可能相差 k;如果 x 和 y 對模 k 不同餘,那麼 x 和 y 不可能相差 k。 因此,我們可以將原陣列按照模 k 分組,然後單獨計算每個分組內部方案數,再根據乘法定理將不同分組的方案數相乘即得到最終結果。
那麼,現在的是如何計算分組內部的方案數?
我們發現,「如果已經選擇過 x - k 或 x + k,則不能選擇 x 」 的語意跟經典動態規劃題 198.打家劫舍 的 「如果兩間相鄰的房屋在同一晚上被小偷闖入,系統會自動報警」 的語意非常類似,我們可以套用相同的解題思路:
1、先對分組內部排序,因為只有相鄰的數才有可能不能同時選擇;
2、定義 dp[i] 表示選擇到 i 為止的方案數,則有遞推關係:
$$
dp[i] = \begin{cases}
dp[i-1] + dp[i-2] &\text{if } a_i - a_{i-1} =k\
dp[i-1]*2 &\text{if } a_i - a_{i-1} \not=k
\end{cases}
$$
如果不選 $a_i$,那麼 $a_{i-1}$ 一定可選,即 $dp[i-1]$ 的方案數。
如果選擇 $a_i$,那麼需要考慮 $a_{i-1}$ 與 $a_i$ 的關係:
- 如果 $a_i - a_{i-1} =k$,那麼 $a_i$ 與 $a_{i-1}$ 不能同時選擇,$dp[i] = dp[i-1] + dp[i-2]$ 表示在 $a_{i-1}$ 和 $a_{i-2}$ 上的方案數之和;
- 如果 $a_i - a_{i-1} \not=k$,那麼 $a_i$ 與 $a_{i-1}$ 可以同時選擇 $dp[i] = dp[i-1]*2$
最後,還需要考慮數位重複的情況,設 c_i 表示 a_i 的出現次數:
- 如果不選 $a_i$,則只有 1 種方案,即空集;
- 如果選擇 $a_i$,則有 $2^{c_i}$ 種方案,最後在減去 1 個空集方案。
整理到遞迴公式中有:
$$
dp[i] = \begin{cases}
dp[i-1] + dp[i-2](2^{c_i}-1) &\text{if } a_i - a_{i-1} =k\
dp[i-1](2^{c_i}) &\text{if } a_i - a_{i-1} \not=k
\end{cases}
$$
以 [2, 3, 4, 5, 10], k = 2 為例,按照模 2 分組後:
- 餘數為 0 的分組 [2, 4, 10]:方案為 [2]、[4]、[10]、[2, 10]、[4, 10]
- 餘數為 1 的分組 [3, 5]:方案為 [3]、[5]
class Solution {
fun beautifulSubsets(nums: IntArray, k: Int): Int {
// 1、同餘分組
// <餘數 to <元素,元素計數>>
val buckets = HashMap<Int, TreeMap<Int, Int>>()
for (num in nums) {
val cntMap = buckets.getOrPut(num % k) { TreeMap<Int, Int>() }
cntMap[num] = cntMap.getOrDefault(num, 0) + 1
}
// 2、列舉分組
var ret = 1
for ((_, bucket) in buckets) {
// 3、動態規劃
val n = bucket.size
// dp[i] 表示選擇到 i 位置的方案數,這裡使用捲動陣列寫法
// val dp = IntArray(n + 1)
var pre2 = 0 // dp[i-2]
var pre1 = 1 // dp[i-1]
var index = 1
var preNum = -1
for ((num, cnt) in bucket) {
if (index > 1 && num - preNum == k) {
// a_i 不可選
val temp = pre1
pre1 = pre1 + pre2 * ((1 shl cnt) - 1)
pre2 = temp
} else {
// a_i 可選可不選
val temp = pre1
pre1 = pre1 * (1 shl cnt)
pre2 = temp
}
preNum = num
index++
}
ret *= pre1
}
return ret - 1
}
}
複雜度分析:
- 時間複雜度:$O(nlgn + n)$ 其中 $n$ 為 $nums$ 陣列的長度,使用有序集合進行分組的時間複雜度是 $O(nlgn)$,列舉分組的步驟每個元素最多存取一次,時間複雜度是 $O(n)$;
- 空間複雜度 $O(n)$:有序集合空間 $O(n)$,動態規劃過程中使用捲動陣列空間為 $O(1)$。
相似題目
近期周賽子集問題:
LeetCode 周賽 333 · 無平方子集計數(Medium)
2598. 執行操作後的最大 MEX(Medium)
題目地址
https://leetcode.cn/problems/smallest-missing-non-negative-integer-after-operations/
題目描述
給你一個下標從 0 開始的整數陣列 nums 和一個整數 value 。
在一步操作中,你可以對 nums 中的任一元素加上或減去 value 。
- 例如,如果
nums = [1,2,3]且value = 2,你可以選擇nums[0]減去value,得到nums = [-1,2,3]。
陣列的 MEX (minimum excluded) 是指其中陣列中缺失的最小非負整數。
- 例如,
[-1,2,3]的 MEX 是0,而[1,0,3]的 MEX 是2。
返回在執行上述操作 任意次 後,nums 的最大 MEX 。

預備知識
- 同餘性質:
如果 x % m == y % m,則稱 x 和 y 對模 m 同餘,即為 x ≡ (y mod m)
- 負數取模技巧:
如果 x 和 y 都大於 0,則 x ≡ (y mod m) 等價於 x % m == y % m
$$
\begin{matrix}
10\ % \ 3 == 1\
-4\ %\ 3 == 1
\end{matrix}
$$
如果 x 和 y 都小於 0,則 x ≡ (y mod m) 等價於 x % m == y % m
$$
\begin{matrix}
-10\ %\ 3== -1\
-4\ %\ 3==-1
\end{matrix}
$$
如果 x < 0,而 y≥0,則 x ≡ (y mod m) 等價於 x % m + m == y % m
$$
\begin{matrix}
-10\ %\ 3== -1 + 3 == 2\
-4\ %\ 3 == -1 + 3 == 2\
5\ %\ 3==2
\end{matrix}
$$
可以看到,為了避免考慮正負數,可以統一使用 (x % m + m) % m 對 x 取模,如此無論 x 為正負數,餘數都能轉換到 [0,m) 範圍內。
題解(同餘分組 + 貪心)
這道題依然考同餘性質。
根據同餘性質,如果 x 和 y 對模 value 同餘,那麼經過若干次操作後 x 總能轉換為 y。如果 x 和 y 對模 value 不同餘,那麼無論經過多少次操作 x 也無法轉換為 y。
舉個例子:{-10、-4、-1、2、5} 都對模 3 同餘,而 1 對模 3 不同餘。只要經過若干次 +value/-value,總能轉換為同餘的其他數;
- -10 + 3 * 2 = -4
- -10 + 3 * 3 = -1
- -10 + 3 * 4 = 2
- -10 + 3 * 5 = 5
- 其它同理。
- -10 無法轉換為 1
貪心思路:繼續分析題目,由於不同分組中的數不可能轉換為其它分組的數,為了讓目標 「確實的最小非負整數儘可能大」 ,應該取儘可能小的同餘數,否則無法使結果更優。
舉個例子,假設 value 為 3,且不同分組的個數如下:
- 餘數為 0 的分組中有 3 個元素:應該取 0、3、6
- 餘數為 1 的分組中有 4 個元素:應該取 1、4、7、10
- 餘數為 2 的分組中有 1 個元素:應該取 2、[缺失 5]
如果餘數為 0 的分組取 0、6、9,則缺失的元素會變成 4。
class Solution {
fun findSmallestInteger(nums: IntArray, value: Int): Int {
// 同餘分組
val buckets = HashMap<Int, Int>()
for (num in nums) {
val mod = (num % value + value) % value
buckets[mod] = buckets.getOrDefault(mod, 0) + 1
}
// 試錯
var mex = 0
while (true) {
val mod = mex % value // mex 一定是非負數
buckets[mod] = buckets.getOrDefault(mod, 0) - 1
// 計數不足
if (buckets[mod]!! < 0) break
mex++
}
return mex
}
}
複雜度分析:
- 時間複雜度:$O(n)$ 其中 $n$ 為 $nums$ 陣列的長度,計數時間為 $O(n)$,試錯最多嘗試 $n$ 次,整體時間複雜度為 $O(n)$;
- 空間複雜度:$O(value)$ 雜湊表最多記錄 $value$ 個分組。
相似題目:
OK,這場周賽就講這麼多,我們下週見。