【LeetCode貪心#12】圖解監控二元樹(正宗hard題,涉及貪心分析、二元樹遍歷以及狀態轉移)
監控二元樹
給定一個二元樹,我們在樹的節點上安裝攝像頭。
節點上的每個攝影頭都可以監視其父物件、自身及其直接子物件。
計算監控樹的所有節點所需的最小攝像頭數量。
範例 1:

對應顏色的攝像頭的覆蓋範圍如圖所示,我們在橙色的節點處放置了攝像頭,其有兩個葉子節點,因此這是符合我們的推斷的
該攝像頭節點的覆蓋範圍包含了其父節點,因此我們無需在其父節點的父節點處放置攝像頭,因為這會導致覆蓋範圍重疊,進而浪費一個覆蓋範圍,這不符合我們設定最少攝像頭的目標
貪心點
這裡還會出現一個問題,就是在根節點處放攝像頭其實也浪費了一個覆蓋範圍(就是其父節點的範圍)
所以如果嚴格按照設定最少攝像頭的目標來做的話,此時我們應該將攝像頭設定在根節點的父節點
但是,實際上這麼做只是在區域性上滿足了最優解,在全域性上並不是最優的
因為葉子節點的數量遠大於根節點的數量,如果按照「在根節點的父節點設定攝像頭」的規則來做的話,那麼會影響到葉子節點設定攝像頭的方法,進而影響最後總攝像頭的數量
因此,不能為了節省根節點浪費的一個範圍犧牲其他更多更合理的攝像頭設定位置
總結一下攝像頭安放原則:優先在葉子節點的父節點安放攝像頭,然後從下往上推,每隔兩個節點再放一個攝像頭,直到遍歷至根節點
狀態設定
(僅用於模擬,無需選擇最優狀態)
通過上面的分析,我們遍歷二元樹的順序自然的應該選擇後序遍歷
問題又來了,怎麼控制每隔兩個節點放一個攝像頭呢?
這裡可以設定幾個狀態,然後記錄每個節點的狀態,根據左右子節點的狀態去確定父節點的狀態
通過節點間的狀態關係,來確定某處是否應該安放攝像頭
根據分析,可以得出以下三種節點狀態:
- 沒被覆蓋(0)
- 有攝像頭(1)
- 被覆蓋(2)
這裡要麼節點是被覆蓋,要麼是沒被覆蓋,沒必要設定一個沒有攝像頭的狀態(有攝像頭其實也是被覆蓋的)
然後這裡需要討論二元樹中空節點的狀態設定問題
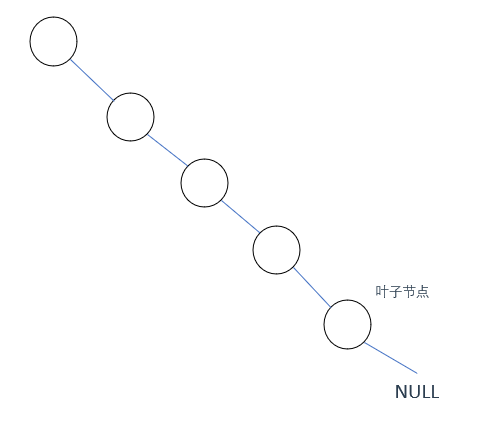
以上述二元樹為例,因為就三種狀態嘛,那這個NULL就有三種情況,看看哪種情況符合我們的要求
情況1: NULL節點沒被覆蓋(0)
因為這個NULL節點被設定為無覆蓋狀態,那按題意一定要有一個攝像頭去覆蓋它,因此NULL的父節點,也就是葉子節點就需要放置攝像頭
而這與我們前面設計的放置原則(優先在葉子節點的父節點安放攝像頭)有衝突,且推到後面,根節點處會沒有攝像頭(反正就是不合適)
因此情況1否了
情況2: NULL節點有攝像頭(1)
這種情況也不行,因為如果NULL節點有攝像頭,就意味著葉子節點已經被覆蓋了
那麼下一步需要隔兩個節點再放置攝像頭,那葉子節點的父節點就又沒有攝像頭了,即又不滿足設計初衷
否了
情況3: NULL節點被覆蓋(2)
前兩種都不行,那這個肯定行了,簡單推一下就知道這種情況是滿足條件的
因此,空節點應該被設定為有覆蓋狀態(2)
狀態轉移
規定好狀態之後,如何在遍歷過程中對每個節點的狀態進行轉換並統計攝像頭個數呢?
這裡又有幾種情況需要討論:(後序遍歷)
情況1:左右子節點都有覆蓋
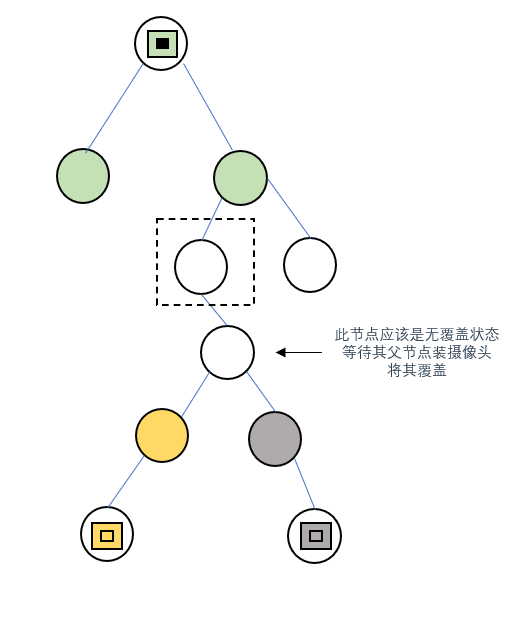
某個節點的左右子節點均被覆蓋時,覆蓋它們的攝像頭肯定是不同的,因此當前節點應該設定為無覆蓋(0),等待之後遍歷到父節點設定攝像頭將其覆蓋
情況2:左右子節點至少有一個無覆蓋
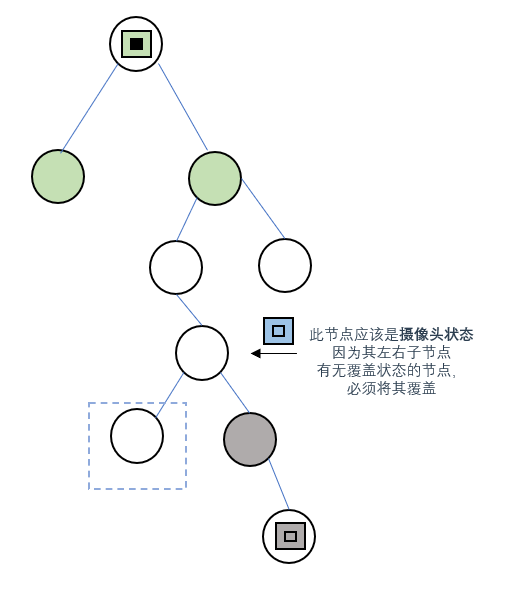
不論左右,當某個節點的子節點出現無覆蓋狀態時,當前節點都應該設定為攝像頭狀態(1),這樣才能不漏掉這個沒被覆蓋的節點
情況3: 左右子節點至少有一個有攝像頭
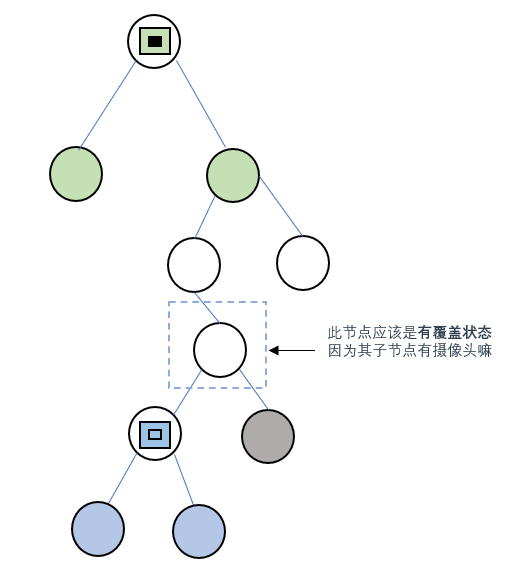
因為攝像頭的覆蓋範圍是三層,某個節點的子節點有攝像頭,那該節點肯定是被覆蓋到了的,因此節點狀態設為有覆蓋(2)
情況4:遍歷完畢根節點還是沒被覆蓋
確實是有這種情況,此時需要對根節點進行單獨修改,放置一個攝像頭(1)
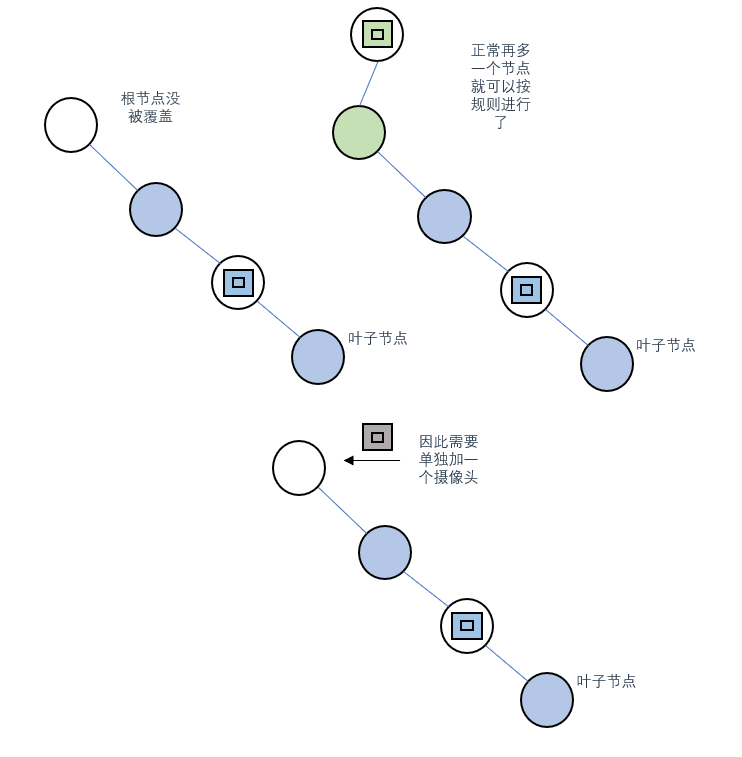
雖然這樣會浪費一個覆蓋範圍,但是也沒辦法
至此,所有狀態轉移的情況分析完畢(夠複雜夠陰間了吧...)
程式碼
要使用後序遍歷,因此可以直接使用二元樹後序遞迴遍歷的模板(詳見)
為了複習之前的知識,這裡還是使用遞迴三部曲的方式寫一下程式碼
遞迴三部曲
1、確定遞迴函數的引數和返回值
根據分析,我們在遍歷二元樹的過程中是通過判斷當前節點的狀態(依據是左右子節點的狀態)來決定是否要設定攝像頭的
因此遞迴的返回值應該是一個節點的狀態(0、1、2其中之一),因此遞迴函數有返回值int
輸入引數肯定是待判斷狀態的節點
class Solution {
private:
int res = 0;//記錄攝像頭數量
int traversal(TreeNode* cur){//確定遞迴函數引數與返回值
}
public:
int minCameraCover(TreeNode* root) {
}
};
2、確定終止條件
遇到葉子節點就終止,和遍歷模板中一致
class Solution {
private:
int res = 0;//記錄攝像頭數量
int traversal(TreeNode* cur){//確定遞迴函數引數與返回值
if(cur == NULL) return 2;//空節點按規則返回2狀態
}
public:
int minCameraCover(TreeNode* root) {
}
};
3、確定單層處理邏輯
這裡就是完成左右中的後序遍歷邏輯就行
需要在中的位置處理我們的3中左右子節點的情況,來給當前節點返回一個狀態(第四種狀態在主函數中處理)
class Solution {
private:
int res = 0;//記錄攝像頭數量
int traversal(TreeNode* cur){//確定遞迴函數引數與返回值
//確定終止條件,遇到葉子節點終止,該節點有覆蓋(因為是空節點)
if(cur == NULL) return 2;
//確定單層處理邏輯,即左右中
int left = traversal(cur->left);//左
int right = traversal(cur->right);//右
//中,處理4種左右節點的情況
if(left == 2 && right == 2) return 0;//左右子節點都有覆蓋(2)
if(left == 0 || right == 0){//左右子節點至少有一個無覆蓋
res++;
return 1;
}
if(left == 1 || right == 1) return 2;//左右子節點至少有一個有攝像頭(1)
return -1;//需要一個返回值,但程式碼不會執行到這
}
public:
int minCameraCover(TreeNode* root) {
}
};
注意,遞迴函數有返回值,需要用變數接一下,並且最後需要給一個返回值-1(儘管不會執行到此處)
完整程式碼
剩下的一種情況是遍歷結束根節點沒被攝像頭覆蓋,我們可以在主函數中處理該情況
只要在呼叫遞迴函數後判斷一下最終返回值是否為0即可(注意返回值不是res)
如果是0表示當前二元樹在遍歷結束後,根節點的狀態沒有變為被覆蓋(2),要多設定一個攝像頭(就讓res再加1即可)
class Solution {
private:
int res = 0;//記錄攝像頭數量
int traversal(TreeNode* cur){//確定遞迴函數引數與返回值
//確定終止條件,遇到葉子節點終止,該節點有覆蓋(因為是空節點)
if(cur == NULL) return 2;
//確定單層處理邏輯,即左右中
int left = traversal(cur->left);//左
int right = traversal(cur->right);//右
//中,處理4種左右節點的情況
if(left == 2 && right == 2) return 0;//左右子節點都有覆蓋(2)
if(left == 0 || right == 0){//左右子節點至少有一個無覆蓋
res++;
return 1;
}
if(left == 1 || right == 1) return 2;//左右子節點至少有一個有攝像頭(1)
return -1;//需要一個返回值,但程式碼不會執行到這
}
public:
int minCameraCover(TreeNode* root) {
//在這裡處理root無覆蓋的情況
if(traversal(root) == 0){//呼叫遞迴進行後序遍歷,如果根節點沒被覆蓋,額外加個攝像頭
res++;
return res;
}
return res;
}
};