紅黑樹的由來及其底層原理
title: 紅黑樹
date: 2022-03-31 10:41:30
sidebar: auto
categories:
- 資料結構
- 二元樹
tags:
- 紅黑樹
一、樹
1.1 樹的定義
- 樹是由n(n>=0)個有限結點組成一個具有層次關係的集合。把它叫做「樹」是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。
- 樹結構是一種非線性儲存結構,儲存的是具有「一對多」關係的資料元素的集合。
1.2 樹的特點
- 每個結點有零個或多個子結點;沒有父結點的結點稱為根結點;每一個非根結點有且只有一個父結點;除了根結點外,每個子結點可以分為多個不相交的子樹;
- 樹是一種特殊的圖
1.3 樹與圖的區別
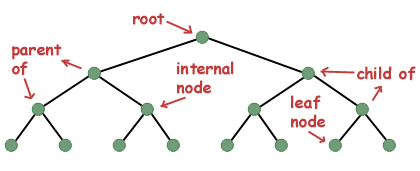

- 樹是沒有環的圖(在圖裡面,環的路線是開始和結束都是一樣的點)一個子節點只有一個父節點,所以樹不是一個遞迴的資料結構。
| Trees | Graphs |
|---|---|
| 1. A tree is a special kind of graph that there are never multiple paths exist. There is always one way to get from A to B. | 1. A graph is a system that has multiple ways to get from any point A to any other point B. |
| 2. Tree must be connected. | 2. Graph may not be connected. |
| 3. Since it connected we can reach from one particular node to all other nodes. This kind of searching is called traversal. | 3. Traversal always not applicable on graphs. Because graphs may not be connected. |
| 4. Tree contains no loops, no circuits. | 4. Graph may contain self-loops, loops. |
| 5. There must be a root node in tree. | 5. There is no such kind of root node in graphs |
| 6. We do traversal on trees. That mean from a point we go to each and every node of tree. | 6. We do searching on graphs. That means starting from any node try to find a particular node which we need. |
| 7. pre-order, in-order, post-order are some kind of traversals in trees. | 7. Breath first search, Depth first search, are some kind of searching algorithms in graphs. |
| 8. Trees are directed acyclic graphs. | 8. Graphs are cyclic or acyclic. |
| 9. Tree is a hierarchical model structure. | 9. Graph is network model. |
| 10. All trees are graphs. | 10. But all graphs are not trees. |
| 11. Based on different properties trees can be classified as Binary tree, Binary search tree, AVL trees, Heaps. | 11. We differ the graphs like directed graphs and undirected graphs. |
| 12. If tree have 「n」 vertices then it must have exactly 「n-1」 edges only. | 12. In graphs number of edges doesn’t depend on the number of vertices. |
| 13. Main use of trees is for sorting and traversing. | 13. Main use of graphs is coloring and job scheduling. |
| 14. Less in complexity compared to graphs. | 14. High complexity than trees due to loops. |
二、二元樹
2.1 什麼是二元樹
2.1.1 定義
- 樹的任意節點至多包含兩棵子樹。
- 是n(n>=0)個結點的有限集合,它或者是空樹(n=0),或者是由一個根結點及兩顆互不相交的、分別稱為左子樹和右子樹的二元樹所組成
2.1.2 特點
- 每個結點最多有兩顆子樹,所以二元樹中不存在度(擁有的子樹數目稱為結點的度)大於2的結點
- 左子樹和右子樹是有順序的,次序不能任意顛倒
- 即使樹中某結點只有一棵子樹,也要區分它是左子樹還是右子樹
2.2 二元樹的分類
2.2.1 滿二元樹
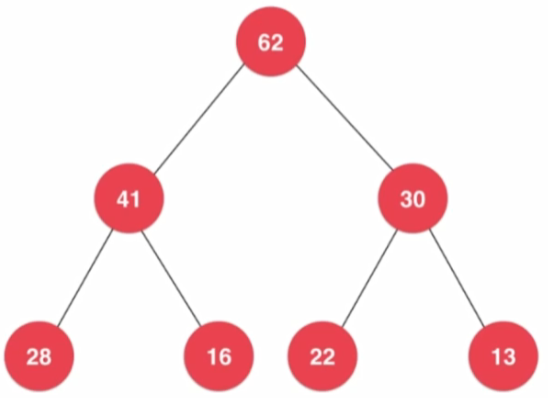
-
除最後一層無任何子節點外,每一層上的所有結點都有兩個子結點的二元樹
-
滿二元樹特點:
-
- 葉子只能出現在最下一層。出現在其它層就不可能達成平衡。
- 非葉子結點的度(結點擁有的子樹數目稱為結點的度)一定是2
- 在同樣深度的二元樹中,滿二元樹的結點個數最多,葉子數最多
2.2.2 完全二元樹
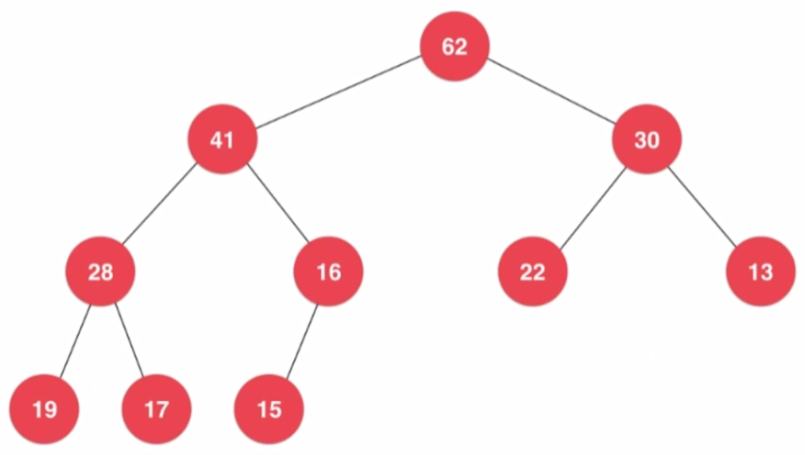
-
除最後一層外,每一層上的結點數均達到最大值;在最後一層上只缺少右邊的若干結點
-
完全二元樹特點:
-
- 葉子結點只能出現在最下層和次下層。
- 最下層的葉子結點集中在樹的左部。
- 倒數第二層若存在葉子結點,一定在右部連續位置。
- 如果結點度為1,則該結點只有左孩子,即沒有右子樹。
- 同樣結點數目的二元樹,完全二元樹深度最小
-
堆的實現一般基於完全二元樹
2.2.3 二元搜尋樹
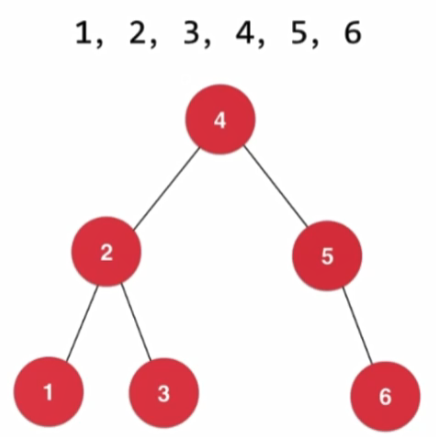
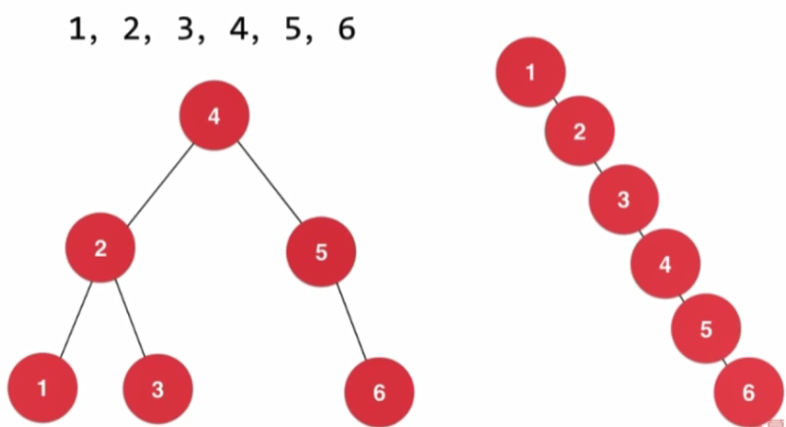
- 可以為空樹,或者是具備如下性質:若它的左子樹不空,則左子樹上的所有結點的值均小於根節點的值;若它的右子樹不空,則右子樹上的所有結點的值均大於根節點的值,左右子樹分別為二叉排序樹。
- 二叉查詢樹是一顆二元樹,它每個結點的值都大於其左子樹的任意結點而小於右子樹的任意結點,它結合了連結串列插入的靈活性和有序陣列查詢的高效性(二分查詢)。
- 對於使用二叉查詢樹的演演算法,它的執行時間取決於樹的形狀,而樹的形狀又取決於結點插入的先後順序。如上圖所示,最好情況下,N 個結點的樹是完全平衡的,每條空連結到根結點的距離都為 ~lgN;而在最壞的情況下,搜尋路徑上可能有 N 個結點,退化成了連結串列。
- 所以,為了保證執行時間始終在對數級別,在動態構建二叉查詢樹時,希望保持其平衡性,也就是降低樹的高度,使其儘可能為 ~lgN,這樣就能保證所有的查詢都能在 ~lgN 次比較內結束,就像二分查詢那樣,這樣的樹被稱為平衡二叉查詢樹。
2.2.4 平衡二叉查詢樹(AVL樹)
什麼是平衡二叉查詢樹
-
由前蘇聯的數學家 Adelse-Velskil 和 Landis 在 1962 年提出的高度平衡的二元樹,根據科學家的英文名也稱為 AVL 樹。它具有如下幾個性質:
-
可以是空樹。
- 假如不是空樹,任何一個結點的左子樹與右子樹都是平衡二元樹,並且高度之差的絕對值不超過 1。
-
平衡之意,如天平,即兩邊的分量大約相同。
-
最早的自平衡二元搜尋樹結構
第一個自平衡二叉查詢樹就是AVL 樹,它規定,每個結點的左右子樹的高度之差不超過 1。在插入或刪除結點,打破平衡後,就會通過一次或多次樹旋轉來重新平衡。
為什麼有平衡二叉查詢樹
- 二元搜尋樹已經在一定程度上提高了搜尋效率,但是由於二元搜尋樹自身的特性,會存在一種極端情況:
平衡二叉查詢樹的缺點
AVL 樹是嚴格平衡的,適用於查詢密集型應用程式,因為在頻繁插入或刪除結點的場景下,它花費在樹旋轉的代價太高。
而紅黑樹就是一種折中方案,它不追求完美平衡,只求部分達到平衡,從而降低在調整時樹旋轉次數。
2.3 二元樹的性質
-
在二元樹的第i層上最多有2 i-1 個節點 。(i>=1)
-
二元樹中如果深度為k,那麼最多有2k-1個節點。(k>=1)
-
n0=n2+1 n0表示度數為0的節點 n2表示度數為2的節點
-
在完全二元樹中,具有n個節點的完全二元樹的深度為[log2n]+1,其中[log2n]+1是向下取整。
-
若對含 n 個結點的完全二元樹從上到下且從左至右進行 1 至 n 的編號,則對完全二元樹中任意一個編號為 i 的結點:
(1) 若 i=1,則該結點是二元樹的根,無雙親, 否則,編號為 [i/2] 的結點為其雙親結點;
(2) 若 2i>n,則該結點無左孩子, 否則,編號為 2i 的結點為其左孩子結點;
(3) 若 2i+1>n,則該結點無右孩子結點, 否則,編號為2i+1 的結點為其右孩子結點
四、紅黑樹
4.1 什麼是紅黑樹
紅黑樹的英文是「Red-Black Tree",簡稱R-B Tree。
紅黑樹是一種二叉查詢樹,通過設定一些規則來保證二元搜尋樹的平衡性,使二元搜尋樹不會在極端情況下變成連結串列。
紅黑樹也是一種平衡二叉查詢樹的變體,它的左右子樹高差有可能大於1,所以紅黑樹不是嚴格意義上的平衡二元樹(AVL),但對之進行平衡的代價較低, 其平均統計效能要強於 AVL。
4.2 紅黑樹的特性
- 每個節點或者是黑色,或者是紅色
- 根節點是黑色
- 每個葉結點(最後的空節點)是黑色
- 如果一個節點是紅色的,則它的子節點必須是黑色的,紅色節點的孩子和父親都不能是紅色
- 從每個葉子到根的所有路徑上不能有兩個連續的紅色節點,任意一結點到每個葉子結點的路徑都包含數量相同的黑結點。確保沒有一條路徑會比其他路徑長出倆倍。
- 因而,紅黑樹是相對接近平衡的二元樹,並不是一個完美平衡二叉查詢樹

為了更好地理解什麼是紅黑樹以及這種看起來特殊的資料結構是如何被提出的,我們首先需要了解一下2-3樹,這種資料結構與紅黑樹是等價的。
說到紅黑樹,就不得不提 2-3 樹,因為,紅黑樹可以說就是它的一種特殊實現,對它有所瞭解,非常有助於理解紅黑樹。
4.3 左傾紅黑樹與2-3樹
4.3.1 什麼是2-3樹
- 保持平衡,無非是為了降低樹的高度,如果把二叉查詢樹一般化,允許一個結點儲存多個值,變成多叉樹,也可認為是降低了高度。
- 結點可以存放一個元素或者兩個元素。相應地,一個結點可能有兩個子樹或者三個子樹。這種結點可以被稱為2結點或者3結點。
- 滿足二分搜尋樹的基本性質,但是它不是一種二元樹。
- 2-3樹是一顆絕對平衡的樹:從根節點到任意一個葉子結點所經過的結點數量一定是相同的。
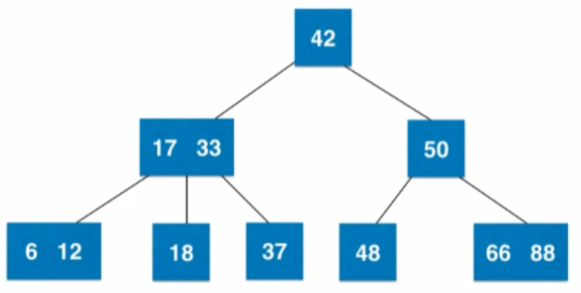
4.3.2 2-3樹的絕對平衡性
- 插入新元素時,並不會建立一個新結點,而是和葉子結點做融合
- 結點的向下分裂和向上融合來保證絕對平衡性
- 插入元素的過程:


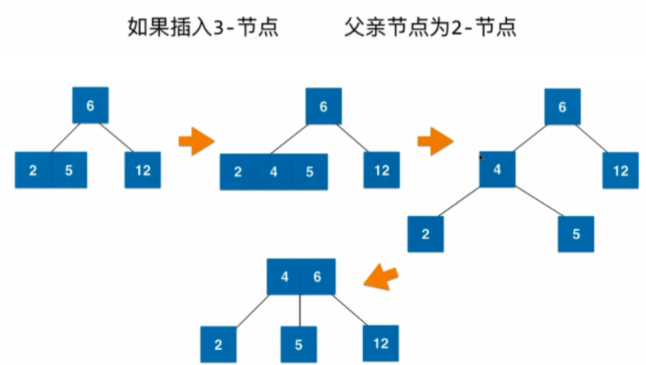
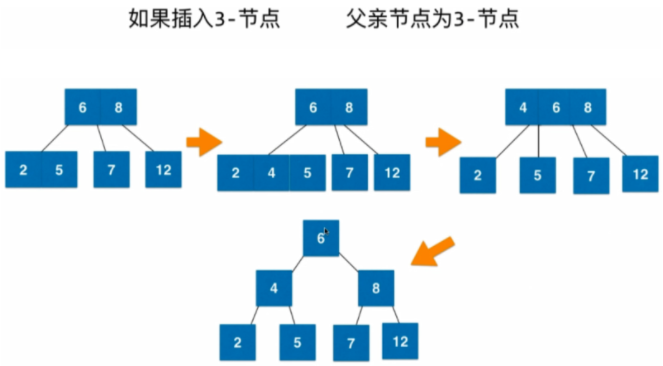
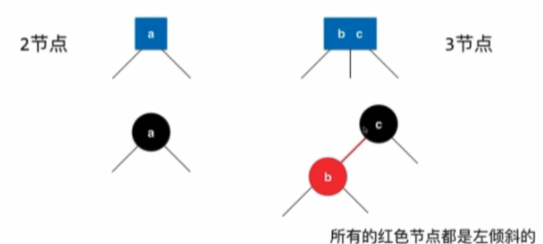
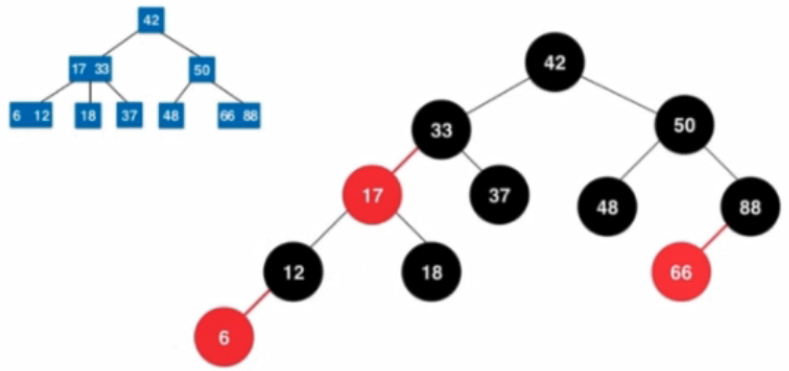
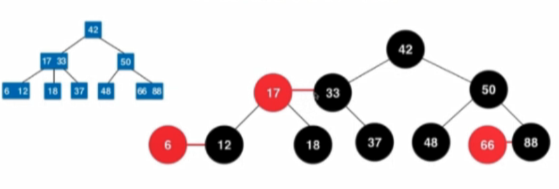
4.3.3 2-3樹與紅黑樹的等價性
- 任意的一顆紅黑樹能夠轉換為一顆2-3樹
- 紅黑樹的根節點一定是黑色的:因為不管2-3樹的根節點是2結點還是3結點,紅黑樹的根節點一定是黑色結點。
- 每個葉子結點(最後的空節點)一定是黑色的:與上一個性質是吻合的。空樹:空節點既是根節點也是葉子結點。
- 如果一個結點是紅色的,它的兩個子節點一定是黑色的。
- 核心性質:從任意一個結點出發,到葉子結點經過的黑色結點數目一定是相同的:紅黑樹中轉換為2-3樹後,不管轉換為2-3樹的2結點還是3結點,一定會有一個結點時黑色的。紅黑樹中每經過一個黑色的結點,意味著對應著經過了原來的2-3樹中的一個結點。
- 紅黑樹是保持「黑平衡」的二元樹。嚴格意義上來講不是平衡二元樹。最大高度:2logn,時間複雜度O(logn)
4.4 左傾紅黑樹新增新元素
與2-3樹新增元素是等價的
2-3 樹插入的都是葉子結點,紅黑樹插入的結點都是紅色的,因為在 2-3 樹中,待插入結點都認為可以插入到一個多值結點中。
4.4.1 樹旋轉
在分析插入和刪除之前,先了解下什麼是樹旋轉。樹旋轉是二元樹中調整子樹的一種操作,常用於調整樹的區域性平衡性,它包含兩種方式,左旋轉和右旋轉。
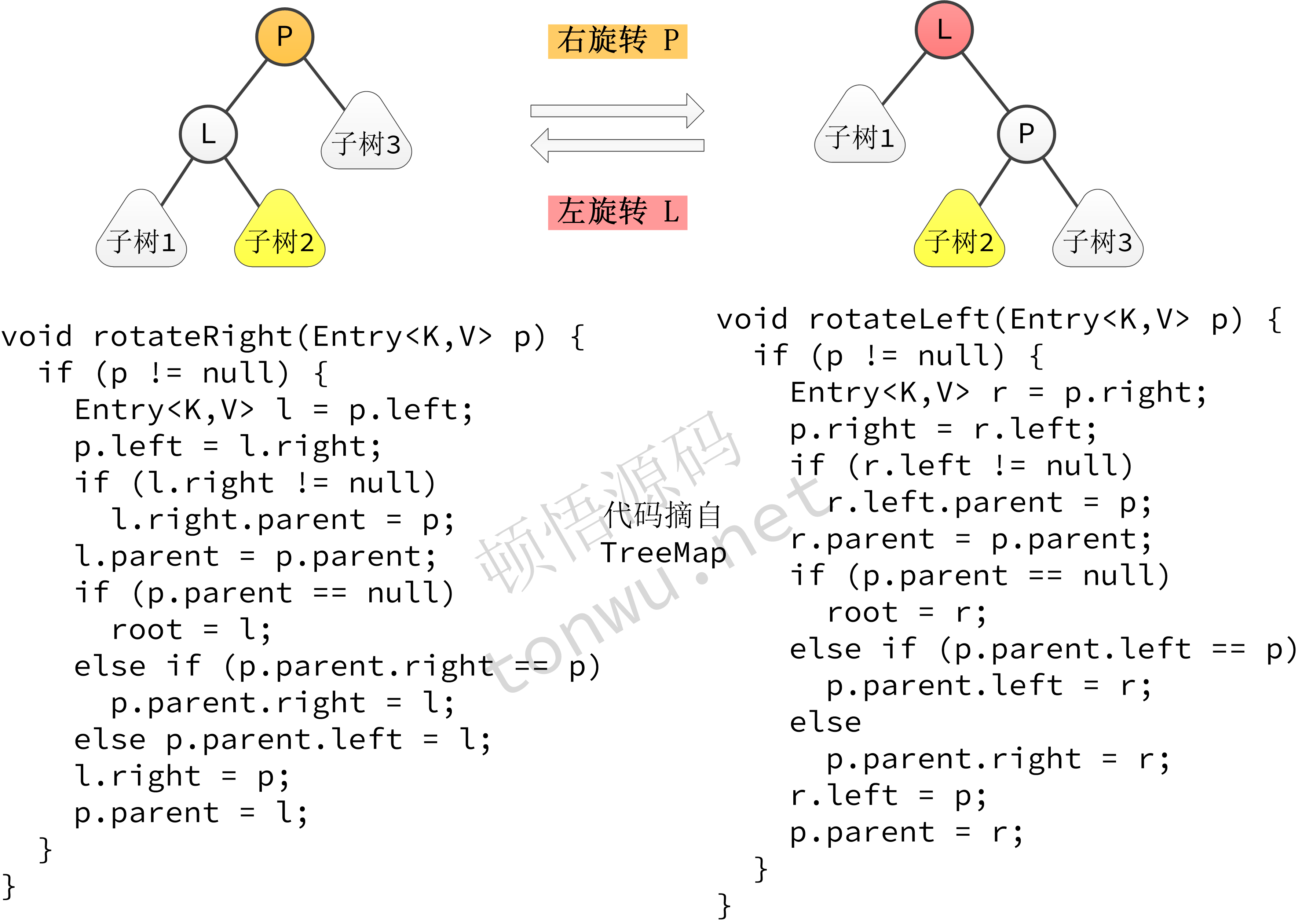
其實旋轉操作很容易理解:左旋轉就是將用兩個結點中的較小者作為根結點變為將較大者作為根結點,右旋轉剛好於此相反,如上圖所示:
- 右旋轉,就是將較小者 L 作為根結點,然後調整 L 和 P 的子樹
- 左旋轉,就是將較大者 P 作為根結點,然後調整 P 和 L 的子樹
紅黑樹的旋轉其實就是為了確保和其結構相同的 2-3樹的一一對應關係,同時保證紅黑樹的有序性和平衡性。
4.4.2 保持根節點為黑色和左旋轉
增加一個元素右傾:進行一次左旋轉
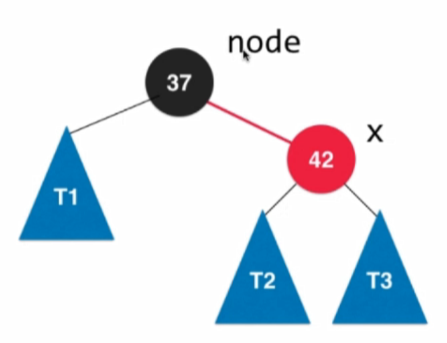

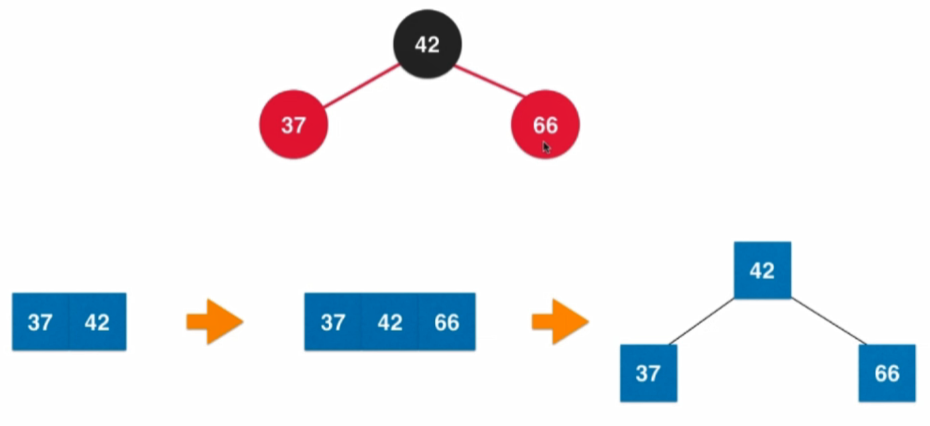
4.4.3 顏色翻轉和右旋轉
顏色翻轉:

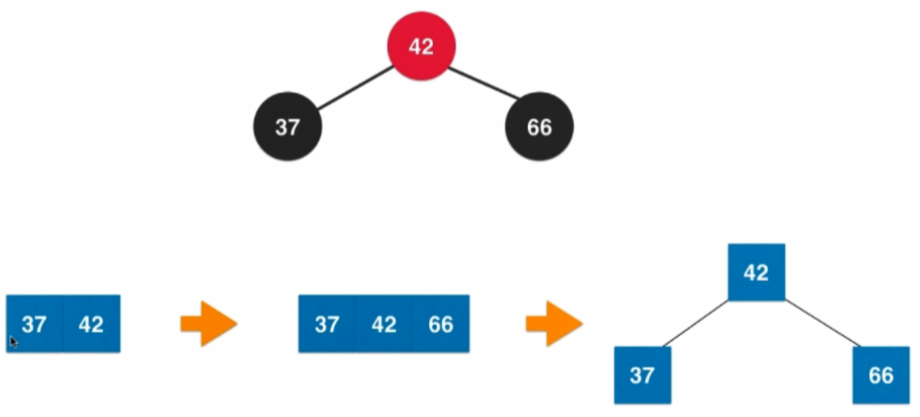
右旋轉:
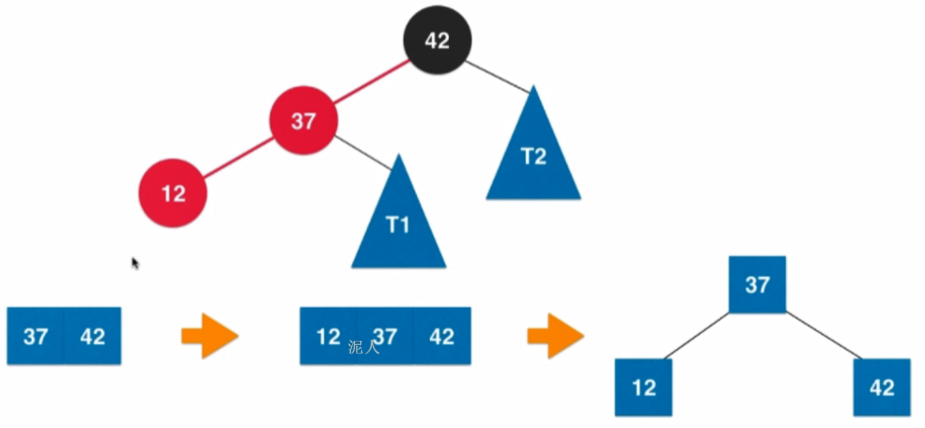
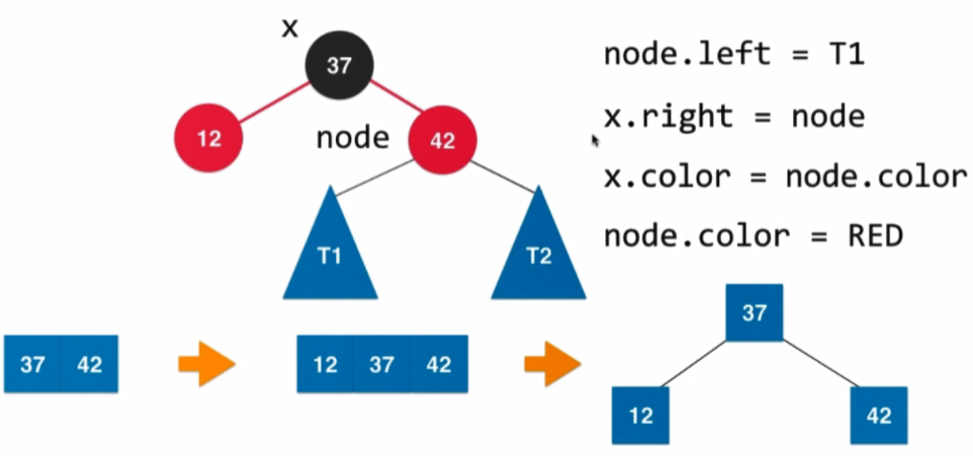
4.4.4 新增新元素完整過程
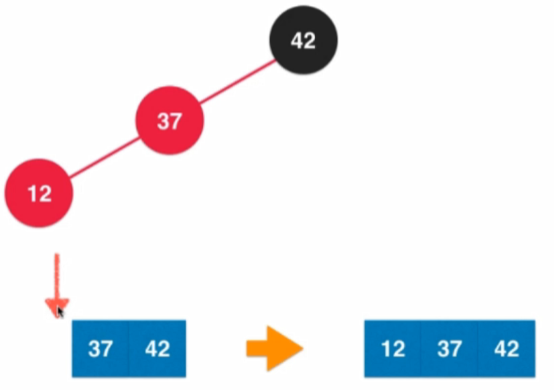
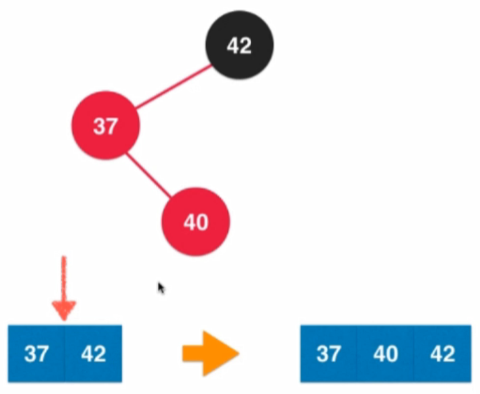
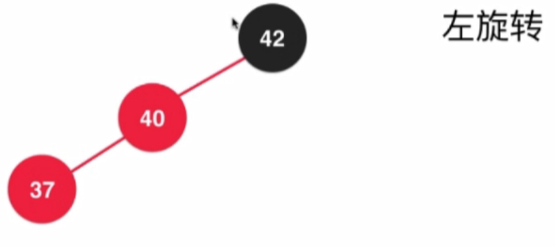
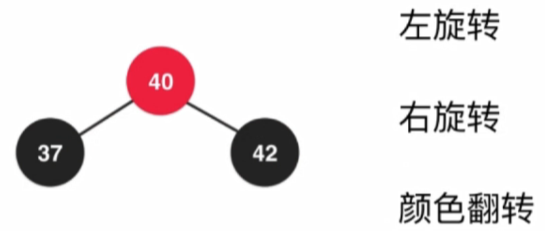
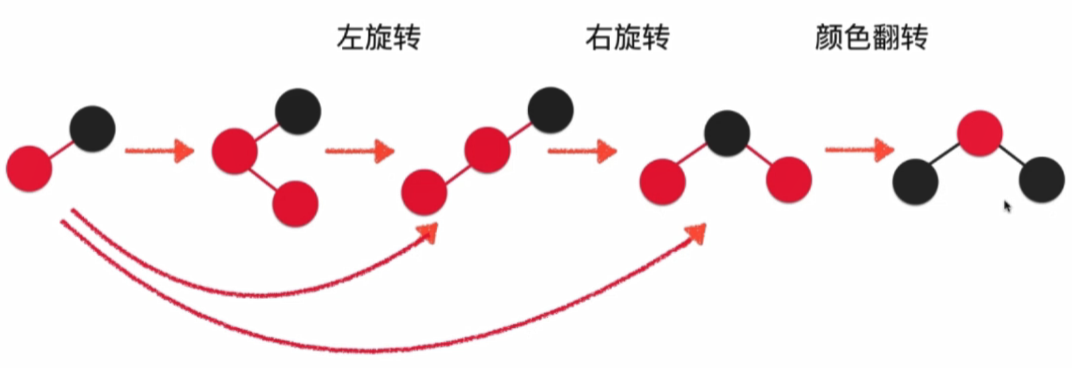
4.4.5 維護紅黑樹平衡的時機
- 左旋轉的時機:當前node的右節點為紅色,且當前結點的左節點不為紅色
- 右旋轉的時機:當前node的左節點為紅色,且左節點的左節點也是紅色
- 顏色翻轉的時機:當前node的左右結點都是紅色
4.5 左傾紅黑樹的實現
左傾紅黑樹(Left-leaning Red-Black Tree)是紅黑樹的一種變種,它的主要思想是將紅色節點向左傾斜,從而簡化插入和刪除操作的實現。在左傾紅黑樹中,所有節點都被標記為紅色或黑色,而且滿足以下性質:
- 根節點是黑色的。
- 所有葉子節點都是黑色的。
- 如果一個節點是紅色的,則它的兩個子節點都是黑色的。
- 任意一條從根節點到葉子節點的路徑上,不能出現連續的兩個紅色節點。
- 從任意一個節點出發到其每個葉子節點的路徑中,黑色節點的個數相同。
下面是左傾紅黑樹的Java程式碼實現:
public class LeftLeaningRedBlackTree<Key extends Comparable<Key>, Value> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private Node root;
private class Node {
private Key key;
private Value val;
private Node left, right;
private boolean color;
public Node(Key key, Value val, boolean color) {
this.key = key;
this.val = val;
this.color = color;
}
}
private boolean isRed(Node x) {
if (x == null) return false;
return x.color == RED;
}
// 坐旋轉,坐旋轉的同時變色
private Node rotateLeft(Node h) {
Node x = h.right;
h.right = x.left;
x.left = h;
x.color = h.color;
h.color = RED;
return x;
}
// 右旋轉,右旋轉的同時變色
private Node rotateRight(Node h) {
Node x = h.left;
h.left = x.right;
x.right = h;
x.color = h.color;
h.color = RED;
return x;
}
private void flipColors(Node h) {
h.color = RED;
h.left.color = BLACK;
h.right.color = BLACK;
}
public void put(Key key, Value val) {
root = put(root, key, val);
root.color = BLACK;
}
private Node put(Node h, Key key, Value val) {
if (h == null) return new Node(key, val, RED);
int cmp = key.compareTo(h.key);
if (cmp < 0) h.left = put(h.left, key, val);
else if (cmp > 0) h.right = put(h.right, key, val);
else h.val = val;
// 左旋
if (isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);
// 右旋
if (isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);
// 顏色翻轉
if (isRed(h.left) && isRed(h.right)) flipColors(h);
return h;
}
}
在這個實現中,我們使用了三種基本操作來維護左傾紅黑樹的性質:
- 左旋(rotateLeft):將一個節點的右子節點向左旋轉,使得它成為新的根節點
- 右旋(rotateRight):將一個節點的左子節點向右旋轉,使得它成為新的根節點
- 顏色翻轉(flipColors):將一個節點的顏色和它的兩個子節點的顏色互換,從而保證每個紅色節點都有一個黑色節點作為父節點
在插入節點時,我們首先按照二元搜尋樹的方式找到要插入的位置,並將節點標記為紅色。然後,我們檢查當前節點的父節點、父節點的兄弟節點和祖父節點的顏色,根據需要進行旋轉和顏色翻轉,以保證左傾紅黑樹的性質不被破壞。
在這個實現中,我們將所有空節點都視為黑色節點,並將根節點標記為黑色。這些約定使得插入操作更加簡單,同時保證了左傾紅黑樹的性質。
總的來說,左傾紅黑樹是一種比較優秀的資料結構,它能夠在保持紅黑樹性質的前提下,簡化插入和刪除操作的實現,同時也能夠保持良好的平衡效能。
4.6 紅黑樹和AVL樹的區別
RB-Tree和AVL樹作為BBST,其實現的演演算法時間複雜度相同,AVL作為最先提出的BBST,貌似RB-tree實現的功能都可以用AVL樹是代替,那麼為什麼還需要引入RB-Tree呢?
- 紅黑樹不追求"完全平衡",即不像AVL那樣要求節點的 |balFact| <= 1,它只要求部分達到平衡,但是提出了為節點增加顏色,紅黑是用非嚴格的平衡來換取增刪節點時候旋轉次數的降低,任何不平衡都會在三次旋轉之內解決,而AVL是嚴格平衡樹,因此在增加或者刪除節點的時候,根據不同情況,旋轉的次數比紅黑樹要多。
- 就插入節點導致樹失衡的情況,AVL和RB-Tree都是最多兩次樹旋轉來實現復衡rebalance,旋轉的量級是O(1)。刪除節點導致失衡,AVL需要維護從被刪除節點到根節點root這條路徑上所有節點的平衡,旋轉的量級為O(logN),而RB-Tree最多隻需要旋轉3次實現復衡,只需O(1),所以說RB-Tree刪除節點的rebalance的效率更高,開銷更小!
- AVL的結構相較於RB-Tree更為平衡,插入和刪除引起失衡,如2所述,RB-Tree復衡效率更高;當然,由於AVL高度平衡,因此AVL的Search效率更高啦。
- 針對插入和刪除節點導致失衡後的rebalance操作,紅黑樹能夠提供一個比較"便宜"的解決方案,降低開銷,是對search,insert ,以及delete效率的折衷,總體來說,RB-Tree的統計效能高於AVL.
- 故引入RB-Tree是功能、效能、空間開銷的折中結果。
AVL更平衡,結構上更加直觀,時間效能針對讀取而言更高;維護稍慢,空間開銷較大。
紅黑樹,讀取略遜於AVL,維護強於AVL,空間開銷與AVL類似,內容極多時略優於AVL,維護優於AVL。
基本上主要的幾種平衡樹看來,紅黑樹有著良好的穩定性和完整的功能,效能表現也很不錯,綜合實力強,在諸如STL的場景中需要穩定表現。
紅黑樹的查詢效能略微遜色於AVL樹,因為其比AVL樹會稍微不平衡最多一層,也就是說紅黑樹的查詢效能只比相同內容的AVL樹最多多一次比較,但是,紅黑樹在插入和刪除上優於AVL樹,AVL樹每次插入刪除會進行大量的平衡度計算,而紅黑樹為了維持紅黑性質所做的紅黑變換和旋轉的開銷,相較於AVL樹為了維持平衡的開銷要小得多
- 總結:實際應用中,若搜尋的次數遠遠大於插入和刪除,那麼選擇AVL,如果搜尋,插入刪除次數幾乎差不多,應該選擇RB。
4.6 紅黑樹的效能
- 對於完全隨機的資料,普通的二元搜尋樹就很好用。
- 對於查詢較多的情況,AVL樹很好用。
- 紅黑樹犧牲了平衡性(2logn的高度),但是紅黑樹的統計效能更優(綜合增刪改查所有操作)。
4.7 紅黑樹的應用
4.7.1 紅黑樹在hashmap中的應用
- 在jdk1.8版本後,Java對HashMap做了改進,在連結串列長度大於8的時候,將後面的資料存在紅黑樹中,以加快檢索速度。
- 紅黑樹是」近似平衡「的。相比avl樹,在檢索的時候效率其實差不多,都是通過平衡來二分查詢。但對於插入刪除等操作效率提高很多。紅黑樹不像avl樹一樣追求絕對的平衡,他允許區域性很少的不完全平衡,這樣對於效率影響不大,但省去了很多沒有必要的調平衡操作,avl樹調平衡有時候代價較大,所以效率不如紅黑樹,在現在很多地方都是底層都是紅黑樹。
- 紅黑樹的高度只比高度平衡的AVL樹的高度(log2n)僅僅大了一倍,在效能上卻好很多。
- HashMap在裡面就是連結串列加上紅黑樹的一種結構,這樣利用了連結串列對記憶體的使用率以及紅黑樹的高效檢索,是一種很happy的資料結構。
- AVL樹是一種高度平衡的二元樹,所以查詢的非常高,但是,有利就有弊,AVL樹為了維持這種高度的平衡,就要付出更多代價。每次插入、刪除都要做調整,就比較複雜、耗時。所以,對於有頻繁的插入、刪除操作的資料集合,使用AVL樹的代價就有點高了。
- 紅黑樹只是做到了近似平衡,並不嚴格的平衡,所以在維護的成本上,要比AVL樹要低。
- 所以,紅黑樹的插入、刪除、查詢各種操作效能都比較穩定。對於工程應用來說,要面對各種異常情況,為了支撐這種工業級的應用,我們更傾向於這種效能穩定的平衡二叉查詢樹。
- java8不是用紅黑樹來管理hashmap,而是在hash值相同的情況下(且重複數量大於8),用紅黑樹來管理資料。 紅黑樹相當於排序資料,可以自動的使用二分法進行定位,效能較高。一般情況下,hash值做的比較好的話基本上用不到紅黑樹。
- 紅黑樹犧牲了一些查詢效能 但其本身並不是完全平衡的二元樹。因此插入刪除操作效率略高於AVL樹。
- AVL樹用於自平衡的計算犧牲了插入刪除效能,但是因為最多隻有一層的高度差,查詢效率會高一些。
4.7.2 紅黑樹在TreeMap和TreeSet的應用
紅黑樹是一種自平衡的二元搜尋樹,它可以在保持二元搜尋樹的性質下,保持樹的高度平衡,從而保證了樹操作的時間複雜度在最壞情況下也是O(log n)。由於其優秀的效能表現,紅黑樹被廣泛應用於Java的TreeMap和TreeSet中。
TreeMap和TreeSet都是基於紅黑樹實現的資料結構,它們分別用於實現基於鍵的有序對映和基於元素的有序集合。它們都支援一系列的操作,如插入、刪除、查詢最大值、查詢最小值、查詢某個鍵或元素的前驅或後繼等操作。
在TreeMap中,每個鍵值對被表示為一個節點,節點按照鍵的大小進行排序,並儲存在一棵紅黑樹中。在TreeSet中,每個元素被表示為一個節點,節點按照元素的大小進行排序,並儲存在一棵紅黑樹中。
由於紅黑樹的自平衡性質,TreeMap和TreeSet能夠在插入、刪除、查詢等操作中保持較為穩定的效能表現,具有很高的效率和可靠性。在Java中,TreeMap和TreeSet被廣泛應用於需要高效實現有序對映和有序集合的場景,如排序、搜尋、去重等場景,是非常常用的資料結構之一。
4.8 紅黑樹的其他實現
演演算法導論中的紅黑樹的實現
package rbTree;
import java.util.HashMap;
/**
* @Author WaleGarrett
* @Date 2021/7/11 18:48
*/
public class RBTree<Key extends Comparable<Key>, Value> {
private class Node<Key, value>{
private Key key;
private Value value;
private Node<Key, Value> left;
private Node<Key, Value> right;
private int color;
public Node(Key key, Value value, int color){
this.key = key;
this.value = value;
this.color = color;
}
}
private static final int RED = 0;
private static final int BLACK = 1;
/**
* 判斷一個結點的顏色是否是紅色
* @param node
* @return
*/
private boolean isRed(Node<Key, Value> node){
if(node == null)
return false;
return node.color == RED;
}
/** node x
* 左旋轉: / \ / \
* @param node T1 x ----> node T3
* @return / \ / \
* T2 T3 T1 T2
*/
private Node<Key, Value> leftRotate(Node<Key, Value> node){
Node x = node.right;
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
/** node x
* 右旋轉: / \ / \
* @param node x T2 ----> T3 node
* @return / \ / \
* T3 T1 T1 T2
*/
private Node<Key, Value> rightRotate(Node<Key, Value> node){
Node x = node.left;
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
/**
* 顏色翻轉:當左右指標均為紅色時進行顏色翻轉
* @param node
*/
private void flipColor(Node<Key, Value> node){
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
/**
* 根節點
*/
private Node<Key, Value> root;
/**
* 新增元素
* @param key
* @param value
*/
public void add(Key key, Value value){
root = add(root, key, value);
// 保證根節點的顏色始終是黑色
root.color = BLACK;
}
public Node add(Node<Key, Value> node, Key key, Value value){
/**
* 新加入的結點始終保持是紅色的
*/
if(node == null)
return new Node<Key, Value>(key, value, RED);
int compare = key.compareTo(node.key);
if(compare < 0){
// key小於當前node結點,新結點必然插入到node的左子樹
node.left = add(node.left, key, value);
}else if(compare > 0){
// key大於當前node結點,新結點必然插入到node的右子樹
node.right = add(node.right, key, value);
}else{
node.value = value;
}
/**
* 使紅黑樹樹保持平衡
*/
// 當node結點的右結點為紅色,而左結點為黑色時,左旋
if(isRed(node.right) && !isRed(node.left))
node = leftRotate(node);
// 當node左側有兩個連續的紅色結點時,右旋
if(isRed(node.right) && isRed(node.right.right))
node = rightRotate(node);
// 當node的左右結點均為紅色時,顏色翻轉
if(isRed(node.left) && isRed(node.right))
flipColor(node);
return node;
}
}