刷爆 LeetCode 雙週賽 100，單方面宣佈第一題最難

本文已收錄到 AndroidFamily，技術和職場問題，請關注公眾號 [彭旭銳] 提問。

大家好，我是小彭。

上週末是 LeetCode 第 100 場雙週賽，你參加了嗎？這場周賽整體沒有 Hard 題，但是也沒有 Easy 題。第一題國服前百名裡超過一半人 wa，很少見。

---

小彭的技術交流群 02 群來了，公眾號回覆 「加群」 加入我們~

---

---

周賽概覽

• 2591. 將錢分給最多的兒童（Easy）
  • 題解一：模擬 $O(1)$
  • 題解二：完全揹包 $O(children·money^2)$
• 2592. 最大化陣列的偉大值（Medium）
  • 題解一：貪心 / 田忌賽馬 $O(nlgn)$
  • 題解二：最大重複計數 $O(n)$
• 2593. 標記所有元素後陣列的分數（Medium）
  • 題解一：排序 O$(nlgn)$
  • 題解二：按照嚴格遞減欄位分組 $O(n)$
• 2594. 修車的最少時間（Medium)
  • 題解一：二分查詢 $O(n + U·log(mc^2))$
  • 題解二：二分查詢 + 計數優化 $O(n·log(mc^2))$

---

2591. 將錢分給最多的兒童（Easy）

題目地址

https://leetcode.cn/problems/distribute-money-to-maximum-children/description/

題目描述

給你一個整數 money ，表示你總共有的錢數（單位為美元）和另一個整數 children ，表示你要將錢分配給多少個兒童。

你需要按照如下規則分配：

• 所有的錢都必須被分配。
• 每個兒童至少獲得 1 美元。
• 沒有人獲得 4 美元。

請你按照上述規則分配金錢，並返回 最多 有多少個兒童獲得 恰好 **8 美元。如果沒有任何分配方案，返回 -1 。

題解一（模擬）

這道題搞數位迷信？發發發 888？

簡單模擬題，但是錯誤率很高，提交通過率僅 19%。

class Solution {
    fun distMoney(money: Int, children: Int): Int {
        var left = money
        // 每人至少分配 1 元
        left -= children
        // 違反規則 2
        if (left < 0) return -1
        // 1、完美：正好所有人可以分配 8 元
        if (left == children * 7) return children
        // 2、溢位：所有人可以分配 8 元有結餘，需要選擇 1 個人分配結餘的金額
        if (left > children * 7) return children - 1
        // 3、不足：儘可能分配 8 元
        var sum = left / 7
        // 結餘金額
        left -= sum * 7
        // 如果結餘 3 元，並且剩下 1 人分配了 1 元，需要破壞一個 8 元避免出現分配 4 美元
        if (left == 3 && children - sum == 1) return sum - 1
        return sum
    }
}

複雜度分析：

• 時間複雜度：$O(1)$
• 空間複雜度：$O(1)$

題解二（完全揹包問題）

競賽中腦海閃現過揹包問題的思路，但第一題暴力才是王道，賽後驗證可行。

• 包裹：最多有 children 人；
• 物品：每個金幣價值為 1 且不可分割，最多物品數為 money 個；
• 目標：包裹價值恰好為 8 的最大個數；
• 限制條件：不允許包裹價值為 4，每個包裹至少裝 1 枚金幣。

令 dp[i][j] 表示分配到 i 個人為止，且分配總金額為 j 元時的最大價值，則有：

• 遞推關係：

$$
dp[i][j]=\sum_{k=1}^{j,k!=4} dp[i-1][j-k] + I(k==8)
$$

• 初始狀態 dp[0][0] = 0
• 終止狀態 dp[children][money]

class Solution {
    fun distMoney(money: Int, children: Int): Int {
        var left = money
        // 每人至少分配 1 元
        left -= children
        // 違反規則 2
        if (left < 0) return -1
        val dp = Array(children + 1) { IntArray(left + 1) { -1 } }
        dp[0][0] = 0
        // i：列舉包裹
        for (i in 1..children) {
            // j：列舉金額
            for (j in 0..left) {
                // k：列舉選項
                for (k in 0..j) {
                    // 不允許選擇 3
                    if (k == 3) continue
                    // 子狀態違反規則
                    if (-1 == dp[i - 1][j - k]) continue
                    // 子狀態 + 當前包裹狀態
                    val cnt = dp[i - 1][j - k] + if (k == 7) 1 else 0
                    dp[i][j] = Math.max(dp[i][j], cnt)
                }
            }
        }
        return dp[children][left]
    }
}

捲動陣列優化：

class Solution {
    fun distMoney(money: Int, children: Int): Int {
        var left = money
        // 每人至少分配 1 元
        left -= children
        // 違反規則 2
        if (left < 0) return -1
        val dp = IntArray(left + 1) { -1 }
        dp[0] = 0
        // i：列舉包裹
        for (i in 1..children) {
            // j：列舉金額
            for (j in left downTo 0) {
                // k：列舉選項
                for (k in 0..j) {
                    // 不允許選擇 3
                    if (k == 3) continue
                    // 子狀態違反規則
                    if (-1 == dp[j - k]) continue
                    // 子狀態 + 當前包裹狀態
                    val cnt = dp[j - k] + if (k == 7) 1 else 0
                    dp[j] = Math.max(dp[j], cnt)
                }
            }
        }
        return dp[left]
    }

複雜度分析：

• 時間複雜度：$O(children·money^2)$
• 空間複雜度：$O(money)$

近期周賽揹包問題：

• LeetCode 周賽 333 · 無平方子集計數（Medium）
• LeetCode 周賽 335 · 獲得分數的方法數（Hard）

---

2592. 最大化陣列的偉大值（Medium）

題目地址

https://leetcode.cn/problems/maximize-greatness-of-an-array/

題目描述

給你一個下標從 0 開始的整數陣列 nums 。你需要將 nums 重新排列成一個新的陣列 perm 。

定義 nums 的 偉大值 為滿足 0 <= i < nums.length 且 perm[i] > nums[i] 的下標數目。

請你返回重新排列 nums 後的 最大 偉大值。

題解一（貪心 / 田忌賽馬）

貪心思路：田忌賽馬，以下賽馬策略最優：

• 田忌的中等馬對齊威王的下等馬，田忌勝；
• 田忌的上等馬對齊威王的中等馬，田忌勝；
• 田忌的下等馬對齊威王的下等馬，齊威王勝。

回到本題，考慮一組貢獻偉大值的配對 $(p, q)$，其中 $p < q$。由於越小的值越匹配到更大值，為了讓結果最優，應該讓 p 儘可能小，即優先匹配 nums 陣列的較小值。那麼 $q$ 如何選擇呢？有 2 種策略：

• 策略 1 - 優先匹配最大值：無法得到最優解，因為會消耗了較大的 q 值，可能導致部分 p 值無法匹配（如果田忌用上等馬對齊威王的下等馬，最終將是齊威王生出）；
• 策略 2- 優先匹配最接近的更大值：最優解，即田忌賽馬策略，以 [1,1,1,2,3,3,5] 為例：
  • 初始狀態 i = 0，j = 0；
  • i = 0，j = 0，無法貢獻偉大值，j 自增 1（尋找最接近的更大值）；
  • i = 0，j = 1， 無法貢獻偉大值，j 自增 1；
  • i = 0，j = 2， 無法貢獻偉大值，j 自增 1；
  • i = 0，j = 3， 貢獻偉大值，j 自增 1，i 自增 1；
  • i = 1，j = 4， 貢獻偉大值，j 自增 1，i 自增 1；
  • i = 2，j = 5， 貢獻偉大值，j 自增 1，i 自增 1；
  • i = 3，j = 6， 貢獻偉大值，j 自增 1，i 自增 1；
  • 退出迴圈，i = 4；正好等於偉大值 4。

class Solution {
    fun maximizeGreatness(nums: IntArray): Int {
        nums.sort()
        // i：參與匹配的指標
        var i = 0
        for (num in nums) {
            // 貢獻偉大值
            if (num > nums[i]) i++
        }
        return i
    }
}

複雜度分析：

• 時間複雜度：$O(nlgn + n)$ 排序 + 線性遍歷，其中 $n$ 是 $nums$ 陣列長度；
• 空間複雜度：$O(lgn)$ 排序遞迴棧空間。

題解二（最大重複計數）

競賽中從測試用例中觀察到題解與最大重複數存在關係，例如：

• 用例 [1,1,1,2,3,3,5]：最大重複數為 3，一個最優方案為 [2,3,3,5,x,x,x]，最大偉大值為 7 - 3 = 4，其中 7 是陣列長度；
• 用例 [1,2,2,2,2,3,5]：最大重複數為 4，一個最優方案為 [2,3,5,x,x,x,x]，最大偉大值為 7 - 4 = 3，其中 7 是陣列長度；
• 用例 [1,1,2,2,2,2,3,3,5]，最大重複數為 4，一個最優方案為 [2,2,3,3,5,x,x,x,x]，最大偉大值為 9 - 4 = 5，其中 9 是陣列長度。

我們發現題目的瓶頸在於數位最大重複出現計數。最大偉大值正好等於 陣列長度 - 最大重複計數。

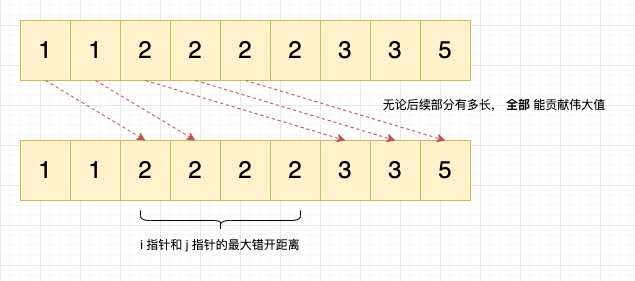
如何證明？關鍵在於 i 指標和 j 指標的最大距離：

當 i 指標指向重複元素的首個元素時（例如下標為 0、2、6 的位置），j 指標必須移動到最接近的較大元素（例如下標為 2，6，8 的位置）。而 i 指標和 j 指標的最大錯開距離取決於陣列重複出現次數最多的元素，只要錯開這個距離，無論陣列後續部分有多長，都能夠匹配上。

class Solution {
    fun maximizeGreatness(nums: IntArray): Int {
        var maxCnt = 0
        val cnts = HashMap<Int, Int>()
        for (num in nums) {
            cnts[num] = cnts.getOrDefault(num, 0) + 1
            maxCnt = Math.max(maxCnt, cnts[num]!!)
        }
        return nums.size - maxCnt
    }
}

複雜度分析：

• 時間複雜度：$O(n)$ 其中 $n$ 是 $nums$ 陣列的長度；
• 空間複雜度：$O(n)$ 其中 $n$ 是 $cnts$ 雜湊表空間。

---

2593. 標記所有元素後陣列的分數（Medium）

題目地址

https://leetcode.cn/problems/find-score-of-an-array-after-marking-all-elements/

題目描述

給你一個陣列 nums ，它包含若干正整數。

一開始分數 score = 0 ，請你按照下面演演算法求出最後分數：

• 從陣列中選擇最小且沒有被標記的整數。如果有相等元素，選擇下標最小的一個。
• 將選中的整數加到 score 中。
• 標記 被選中元素，如果有相鄰元素，則同時標記 與它相鄰的兩個元素 。
• 重複此過程直到陣列中所有元素都被標記。

請你返回執行上述演演算法後最後的分數。

題解一（排序）

這道題犯了大忌，沒有正確理解題意。一開始以為 「相鄰的元素」 是指未標記的最相鄰元素，花了很多時間思考如何快速找到左右未標記的數。其實題目沒有這麼複雜，就是標記陣列上的相鄰元素。

如此這道題只能算 Medium 偏 Easy 難度。

class Solution {
    fun findScore(nums: IntArray): Long {
        // 小頂堆（索引）
        val heap = PriorityQueue<Int>() { i1, i2 ->
            if (nums[i1] != nums[i2]) nums[i1] - nums[i2] else i1 - i2
        }.apply {
            for (index in nums.indices) {
                offer(index)
            }
        }
        var sum = 0L
        while (!heap.isEmpty()) {
            val index = heap.poll()
            if (nums[index] == 0) continue
            // 標記
            sum += nums[index]
            nums[index] = 0
            // 標記相鄰元素
            if (index > 0) nums[index - 1] = 0
            if (index < nums.size - 1) nums[index + 1] = 0
        }
        return sum
    }
}

複雜度分析：

• 時間複雜度：$O(nlgn)$ 堆排序時間，其中 $n$ 是 $nums$ 陣列長度；
• 空間複雜度：$O(n)$ 堆空間。

題解二（按照嚴格遞減欄位分組）

思路參考：靈茶山艾府的題解

按照嚴格遞減欄位分組，在找到坡底後間隔累加 nums[i]，nums[i - 2]，nums[i - 4]，並從 i + 2 開始繼續尋找坡底。

class Solution {
    fun findScore(nums: IntArray): Long {
        val n = nums.size
        var sum = 0L
        var i = 0
        while (i < nums.size) {
            val i0 = i // 坡頂
            while (i + 1 < n && nums[i] > nums[i + 1]) i++ // 尋找坡底
            for (j in i downTo i0 step 2) { // 間隔累加
                sum += nums[j]
            }
            i += 2 // i + 1 不能選
        }
        return sum
    }
}

複雜度分析：

• 時間複雜度：$O(n)$ 其中 $n$ 是 $nums$ 陣列的長度，每個元素最多存取 2 次；
• 空間複雜度：$O(1)$ 只使用常數空間。

---

2594. 修車的最少時間（Medium)

題目地址

https://leetcode.cn/problems/minimum-time-to-repair-cars/

題目描述

給你一個整數陣列 ranks ，表示一些機械工的 能力值 。ranksi 是第 i 位機械工的能力值。能力值為 r 的機械工可以在 r * n2 分鐘內修好 n 輛車。

同時給你一個整數 cars ，表示總共需要修理的汽車數目。

請你返回修理所有汽車 最少 需要多少時間。

注意： 所有機械工可以同時修理汽車。

題解（二分查詢）

我們發現問題在時間 t 上存在單調性：

• 假設可以在 t 時間內修完所有車，那麼大於 t 的時間都能修完；
• 如果不能在 t 時間內修完所有車，那麼小於 t 的時間都無法修完。

因此，我們可以用二分查詢尋找 「可以修完的最小時間」：

• 二分的下界：1；
• 二分的上界：將所有的車交給能力值排序最高的工人，因為他的效率最高。

class Solution {
    fun repairCars(ranks: IntArray, cars: Int): Long {
        // 尋找能力值排序最高的工人
        var minRank = Integer.MAX_VALUE
        for (rank in ranks) {
            minRank = Math.min(minRank, rank)
        }
        var left = 1L
        var right = 1L * minRank * cars * cars
        // 二分查詢
        while (left < right) {
            val mid = (left + right) ushr 1
            if (check(ranks, cars, mid)) {
                right = mid
            } else {
                left = mid + 1
            }
        }
        return left
    }

    // return 能否在 t 時間內修完所有車
    private fun check(ranks: IntArray, cars: Int, t: Long): Boolean {
        // 計算並行修車 t 時間能修完的車（由於 t 的上界較大，carSum 會溢位 Int）
        var carSum = 0L
        for (rank in ranks) {
            carSum += Math.sqrt(1.0 * t / rank).toLong()
        }
        return carSum >= cars
    }
}

複雜度分析：

• 時間複雜度：$O(n·log(mc^2))$ 其中 $n$ 是 $ranks$ 陣列長度，$m$ 是 $ranks$ 陣列的最小值，$c$ 是車輛數量，二分的次數是 $O(log(mc^2))$，每次 $check$ 操作花費 $O(n)$ 時間；
• 空間複雜度：$O(1)$ 僅使用常數級別空間。

題解二（二分查詢 + 計數優化）

我們發現 $ranks$ 的取值範圍很小，所有可以用計數優化每次 $check$ 操作的時間複雜度：

class Solution {
    fun repairCars(ranks: IntArray, cars: Int): Long {
        // 尋找能力值排序最高的工人
        val cnts = IntArray(101)
        var minRank = Integer.MAX_VALUE
        for (rank in ranks) {
            minRank = Math.min(minRank, rank)
            cnts[rank]++
        }
        var left = 1L
        var right = 1L * minRank * cars * cars
        // 二分查詢
        while (left < right) {
            val mid = (left + right) ushr 1
            if (check(ranks, cars, cnts, minRank, mid)) {
                right = mid
            } else {
                left = mid + 1
            }
        }
        return left
    }

    // return 能否在 t 時間內修完所有車
    private fun check(ranks: IntArray, cars: Int, cnts: IntArray, minRank: Int, t: Long): Boolean {
        // 計算並行修車 t 時間能修完的車（由於 t 的上界較大，carSum 會溢位 Int）
        var carSum = 0L
        for (rank in minRank..100) {
            if (cnts[rank] == 0) continue
            carSum += cnts[rank] * Math.sqrt(1.0 * t / rank).toLong()
        }
        return carSum >= cars
    }
}

複雜度分析：

• 時間複雜度：$O(n + U·log(mc^2))$ 其中 $n$ 是 $ranks$ 陣列長度，$m$ 是 $ranks$ 陣列的最小值，$U$ 是 $ranks$ 陣列的取值範圍，$c$ 是車輛數量，二分的次數是 $O(log(mc^2))$，每次 $check$ 操作花費 $O(U)$ 時間；
• 空間複雜度：$O(U)$ $cnts$ 計數陣列空間。

近期周賽二分查詢題目：

• LeetCode 332 · 統計公平數對的數目（Medium）
• LeetCode 334 · 在網格圖中存取一個格子的最少時間（Hard）

這場周賽就這麼多，我們下週見。