前言

在計算機執行過程中，由於種種原因致使資料在儲存過程中可能出現差錯。為了能及時發現錯誤並及時糾正錯誤，通常使用一些編碼方式。

奇偶校驗

奇偶校驗是一種新增一個奇偶位用來指示之前的資料中包含有奇數還是偶數個1的檢驗方式。

對於一個二進位制數：$b_nb_{n-1}...b_2b_1$，新增一個校驗位s，採取偶校驗，即校驗位使新資料中的1的個數為偶數。

新資料：$b_nb_{n-1}...b_2b_1s$。

即 $b_n \oplus b_{n-1} \oplus ... \oplus b_2 \oplus b_1 \oplus s = 0$，則$s = b_n \oplus b_{n-1} \oplus ... \oplus b_2 \oplus b_1$。

在傳輸過程中，如果只有1位（奇數個位）發生了改變（包括校驗位），那麼將可以檢測出來錯誤。但是如果有偶數個位發生了改變，那麼校驗位將是正確的，因此不能檢測錯誤。而且，即使出現了錯誤，也不知道是哪一位出現了錯誤，資料必須整體丟棄並且重新傳輸。

漢明碼

簡介

漢明碼的實質上是多重奇偶校驗，通過巧妙的分組，實現了校驗並糾正一位錯誤的能力。

編碼糾錯理論

任何一種編碼是否具有檢測能力和糾錯能力，都與編碼的最小距離有關。所謂編碼最小距離，是指在一種編碼系統中，任意兩組合法程式碼之間的最少二進位制位數的差異。

根據糾錯理論得：

$ L -1 = D + C \ 且 \ (D \ge C)$

即編碼最小距離L越大，則其檢測錯誤的位數D越大，糾正錯誤的位數C也越大，且糾錯能力恆小於或等於檢錯能力。

所以，如果我們在資訊編碼中增加若干位檢測位，增大L，顯然便能提高檢錯和糾錯能力。漢明碼就是根據這一理論提出的具有一位糾錯能力的編碼。

關於編碼最小距離

例1.1

假設我們的一種編碼系統是所有的3位二進位制數，即$設集合 S =\left\{ 000，001，010，011，100，101，110，111 \right\}$。

那麼對於任何一個資料，比如我們傳輸$010$這個資料，它發生錯誤會改變為：

第一位0變為1：$110$
第二位1變為0：$000$
第三位0變為1：$011$

顯然，這三種資料都在集合當中，我們檢驗不出錯誤。

此時就是，$L = 1$，那麼$0 = D + C$。

例1.2

$設集合 S =\left\{ 001，010，100 \right\}$。

可以看出，我們的編碼最小距離為2，$L = 2$，那麼$1 = D+C$，那麼$D = 1, C = 0$。即，可以檢一位錯，不能糾錯。

比如，我們傳輸資料$010$：

第一位0變為1：$110$
第二位1變為0：$000$
第三位0變為1：$011$

但是，$110,000,011$均不在集合S中，所以我們可以判斷這是出錯了，那怎麼糾錯呢？

對於出錯資料$110$，它的可能正確資料：

第一位0變為1：$010$
第二位0變為1：$100$
第三位1變為0：$111$（不存在S中）

所以是會有兩種情況，故，無法糾錯。

例1.3

$設集合 S =\left\{ 000，111 \right\}$。

則，$L = 3, D = 1 \;且 \;C= 1 \;或\; D = 2\;且\; C = 0$。

核心公式

設欲檢測的二進位制程式碼為n位，為使其具有糾錯能力，需增添k位檢測位，組成 n + k 位的程式碼。為了能準確對錯誤定位以及指出程式碼沒錯，新增添的檢測位數 k應滿足：

$2^k \ge n + k + 1$

變換一下：

$2^k - 1\ge n + k $

k位檢測位可以提供$2^k$種狀態，減去一種正確的狀態，即，所有錯誤的狀態應該包括分別每一位出錯的情況，這裡每一位出錯包括檢測位，所以就是$n + k$。

這樣是不是更好理解。

由此求出不同程式碼長度 n，所需檢測位的位數 k：

n	K（最小）
1	2
2~4	3
5~11	4
12~26	5
27~57	6
58~120	7

分組

k的位數確定後，便可由它們所承擔的檢測任務設定它們在傳送程式碼中的位置及它們的取值。

設$n + k$位程式碼自左至右依次編為第$1,2,3,···,n + k$，而將$k$位檢測位記作$C_i(i = 1,2,4,8,···)$，分別安插在$n + k$位程式碼編號的第$1,2,4,8,···,2^{k-1}位上$。

$C_1$：檢測的$g_1$小組包含1，3，5，7，9，11，··· 位。
$C_2$：檢測的$g_2$小組包含2，3，6，7，10，11，14，15，··· 位。
$C_4$：檢測的$g_3$小組包含4，5，6，7，12，13，14，15，··· 位。
··········

這種小組的劃分有以下特點：

每個小組$g_i$有一位且僅有一位為它所獨佔，這一位是其他小組所沒有的，即$g_i$小組獨佔第$2^{i-1}$位（$i = 1,2,3,···$）。
每兩個小組$g_i$和$g_j$共同佔有一位是其他小組沒有的，即每兩個小組$g_i$和$g_j$共同佔有第$2^{i - 1} + 2^{j - 1}$位（$i,j = 1,2,···$）。
每3個小組$g_i,g_j和g_l共同佔有第$$2^{i -1} + 2^{j - 1} + 2^{l - 1}$位，是其他小組所沒有的。
依次類推。

特點似乎有點不明所以，總結起來就是：

$g_1小組$：位數為 $xxx1$ 的二進位制數表示。
$g_2小組$：位數為 $xx1x$ 的二進位制數表示。
$g_3小組$：位數為 $x1xx$ 的二進位制數表示。
······

稍後，我們會明白這樣設計的緣由。

現在我們需要傳遞一個4位元二進位制數，記為$b_4b_3b_2b_1$。

那麼根據前面的核心公式 $2^k \ge n + k + 1$，可以求出最小的 k為3。

二進位制序號	1	2	3	4	5	6	7
名稱	$C_1$	$C_2$	$b_4$	$C_4$	$b_3$	$b_2$	$b_1$

則，根據配偶原則：

$C_1 \oplus b_4 \oplus b_3 \oplus b_1 = 0$

$C_2 \oplus b_4 \oplus b_2 \oplus b_1 = 0$

$C_4 \oplus b_3 \oplus b_2 \oplus b_1 = 0$

例2

令$b_4b_3b_2b_1 = 1101$，則：

$C_1 = b_4 \oplus b_3 \oplus b_1 = 1 \oplus 1 \oplus 1= 1$

$C_2 = b_4 \oplus b_2 \oplus b_1 = 1 \oplus 0 \oplus 1 =0$

$C_4 = b_3 \oplus b_2 \oplus b_1 = 1 \oplus 0 \oplus 1 = 0$

故 0101的漢明碼應為$C_1C_2b_4C_4b_3b_2b_1$，即1010101。

糾錯過程

漢明碼的糾錯過程實際上就是對配偶原則（或者奇）的檢驗，根據新資料的狀態，便可直接指出錯誤的位置。直接看例子：

例3

已知，傳送的正確漢明碼是$1010101$（配偶原則），傳送後接受到的漢明碼為$1010111$：

二進位制序號	1	2	3	4	5	6	7
傳送的漢明碼	1	0	1	0	1	0	1
接收的漢明碼	1	0	1	0	1	1	1

檢測：

$P_4 = 4 \oplus 5 \oplus 6 \oplus 7 = 0 \oplus 1 \oplus 1 \oplus 1 = 1$
$P_2 = 2 \oplus 3 \oplus 6 \oplus 7 = 0 \oplus 1 \oplus 1 \oplus 1 = 1$
$P_1 = 1 \oplus 3 \oplus 5 \oplus 7 = 1 \oplus 1 \oplus 1 \oplus 1 = 0$

可見，$P_4 和 P_2$都不為 0，顯然出錯了。

那如何找出錯誤呢？

這裡是假設只出現一位錯誤，因為此時的$L = 3$，只能檢一位錯，糾一位錯。

因為$P_1 = 0$，所以可以認為 $1，3，5，7$都沒有錯。
$P_4 = 1，P_2 = 1$，說明 $4，5，6，7$中有一位錯， $2，3，6，7$中有一位錯。
那現在錯誤的範圍就縮小到了，$4，6$中有一位是錯的，$2，6$中有一位錯的。
顯然，第6位是錯的。

此時，更加巧合的是：二進位制數$P_4P_2P_1 = 110$恰好是$6$。

換句話說，檢測出的資訊所表示的數就是出錯的位置。

韋恩圖

我們用韋恩圖來表示一下剛剛找錯誤位的過程：

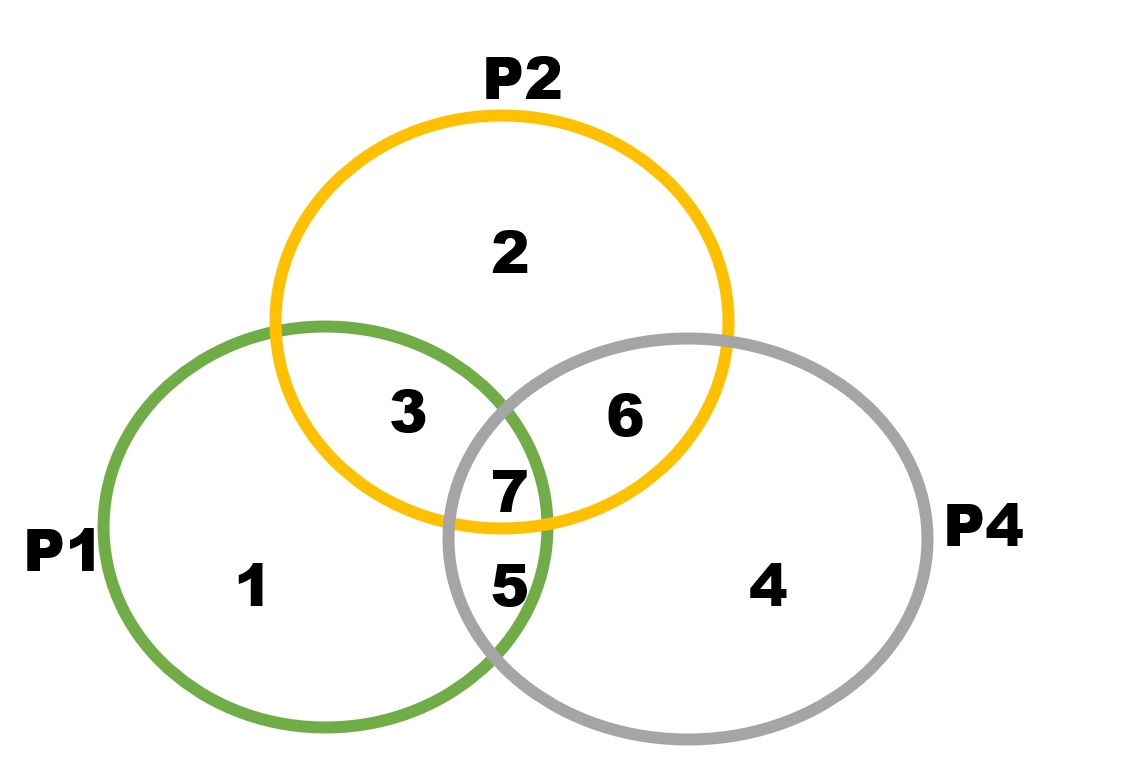
剛剛找 6的過程不就是：$\neg P_1 \cap P_2 \cap P_4$，這樣十分巧妙地利用集合就找出了錯誤的位。

這樣可以理解之前設計的原因了吧。

參考文獻

維基百科

唐朔飛. 計算機組成原理[M]. 第3版. 高等教育出版社, 2020.

記憶體的校驗：漢明碼

前言