靈感來源: https://zhuanlan.zhihu.com/p/91582909

最近實在是被動態規劃傷透了腦筋，今天看到這篇文章感覺醍醐灌頂一般的突然就茅塞頓開，記好這三步，動態規劃就不難了，這裡開篇文章記錄一下，我是如何用這個方法來刷劍指offer的動態規劃題的；
當然每個題都有更好的解決方法，但是我們的思路是先用陳咬金的三板斧解決了問題再來進行優化，下面簡述一下思路:

第一步： 下定義
定義要求解的問題為合適的結構，一般都是一維陣列或二維陣列；

第二步驟：定初值
根據題目給出的範例，確定陣列的前幾位的初始值；

第三步驟：找關係
根據簡單的題目範例，找出陣列元素之間的關係式，類似數學歸納法從簡單的開始往後推導；
前兩步都很簡單，問題的關鍵在於第三步找關係，上檔次一點叫找狀態轉移方程，low一點就是小孩子說的找規律，找到規律，根據這個規律從初始值開始往下走就能找出結果！

tip： 需要注意一些題目的限定條件，比如陣列溢位等等，下面就是最簡單的例子

一、簡單的一維DP

劍指 Offer 10- I. 斐波那契數列

寫一個函數，輸入 n ，求斐波那契（Fibonacci）數列的第 n 項（即 F(N)）。斐波那契數列的定義如下：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契數列由 0 和 1 開始，之後的斐波那契數就是由之前的兩數相加而得出。

答案需要取模 1e9+7（1000000007），如計算初始結果為：1000000008，請返回 1。
0<= n <=100

1、三板斧解決問題

這裡不會放程式碼，只會解釋程式碼，要想真的弄懂還得自己去敲才行；
第一步： 下定義
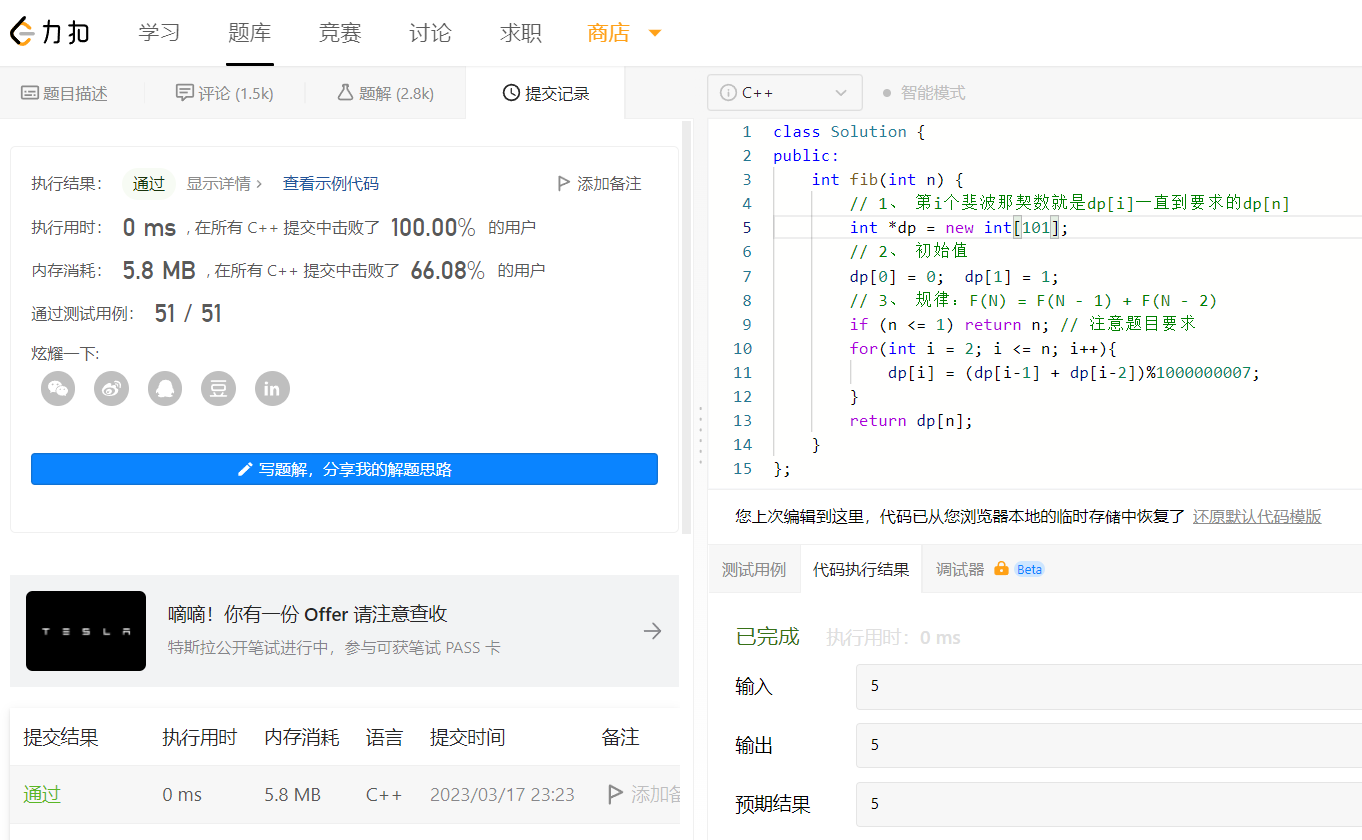
要求第n的斐波那契數，就定義一個n長度的陣列唄，但是這裡題目提示了n最大100，所以我定義了dp[101]

第二步驟：定初值
看題目就能知道 dp[0] = 0; dp[1] = 1;

第三步驟：找關係
這個題目是直接給出來的規律F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
那就直接敲程式碼唄dp[i] = (dp[i-1] + dp[i-2])%1000000007; 搞定最後遍歷一遍返回值就行

需要注意的細節：
注意數值溢位問題:答案需要取模 1e9+7（1000000007）
遍歷需要從2開始，不然陣列會越界，其實假如你注意了題目給出的 N > 1. 這個條件的話，可以忽略這條

2、優雅的解決問題

這裡我們會發現，迴圈那個地方來來回回也就dp[i]、dp[i-1]、dp[i-2]三個變數來回的變，我們可以優化程式碼用三個變數來代替陣列從而節省記憶體！

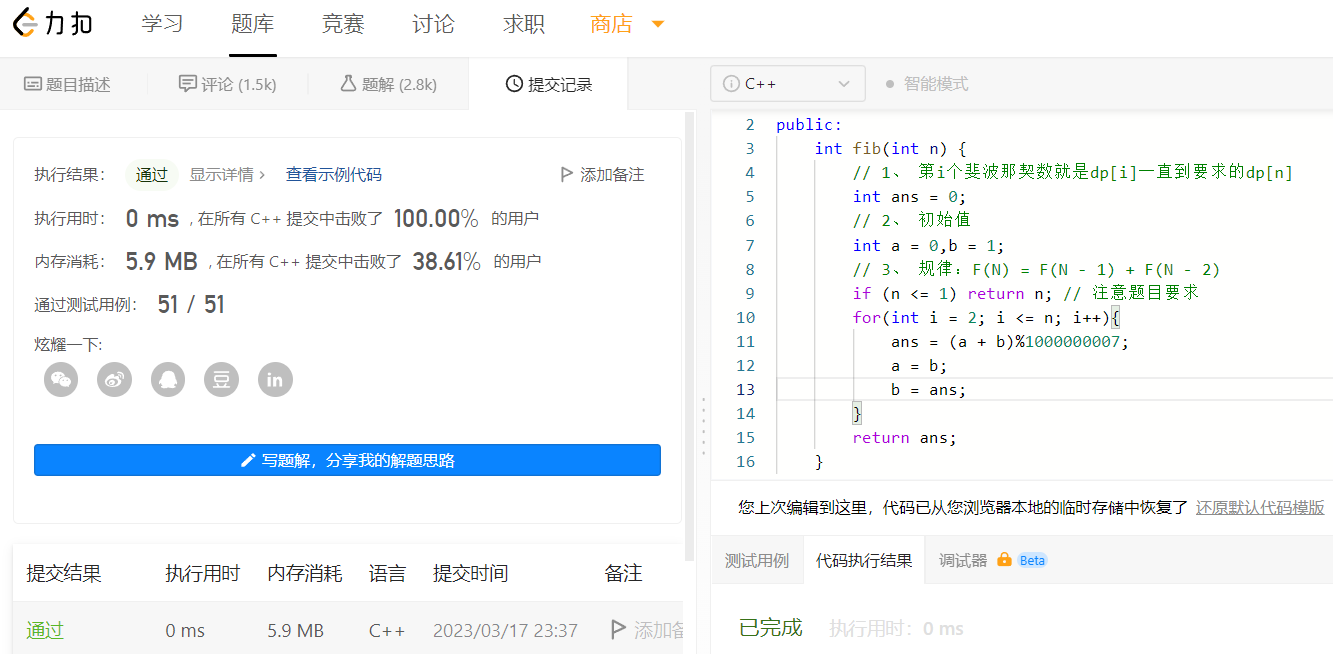
這裡三板斧用的是一維陣列，後來優化了空間複雜度，然鵝這只是簡單的入門題目，大部分情況動態規劃都是二維陣列，好了思路也講了，案例實操也講了，用這三板斧嘗試一下 青蛙跳臺階問題吧，或許你也可以優雅的解決問題，這兩個題目是一樣的道理，接下來講一個規律不會直接給你而是需要自己去找的題目；

劍指 Offer 63 股票的最大利潤

假設把某股票的價格按照時間先後順序儲存在陣列中，請問買賣該股票一次可能獲得的最大利潤是多少？
範例 1:
輸入: [7,1,5,3,6,4]
輸出: 5
解釋: 在第 2 天（股票價格 = 1）的時候買入，在第 5 天（股票價格 = 6）的時候賣出，最大利潤 = 6-1 = 5
注意利潤不能是 7-1 = 6, 因為賣出價格需要大於買入價格。

範例 2:
輸入: [7,6,4,3,1]
輸出: 0
解釋: 在這種情況下, 沒有交易完成, 所以最大利潤為 0。

限制：
0 <= 陣列長度 <= 10^5

1、三板斧解決問題

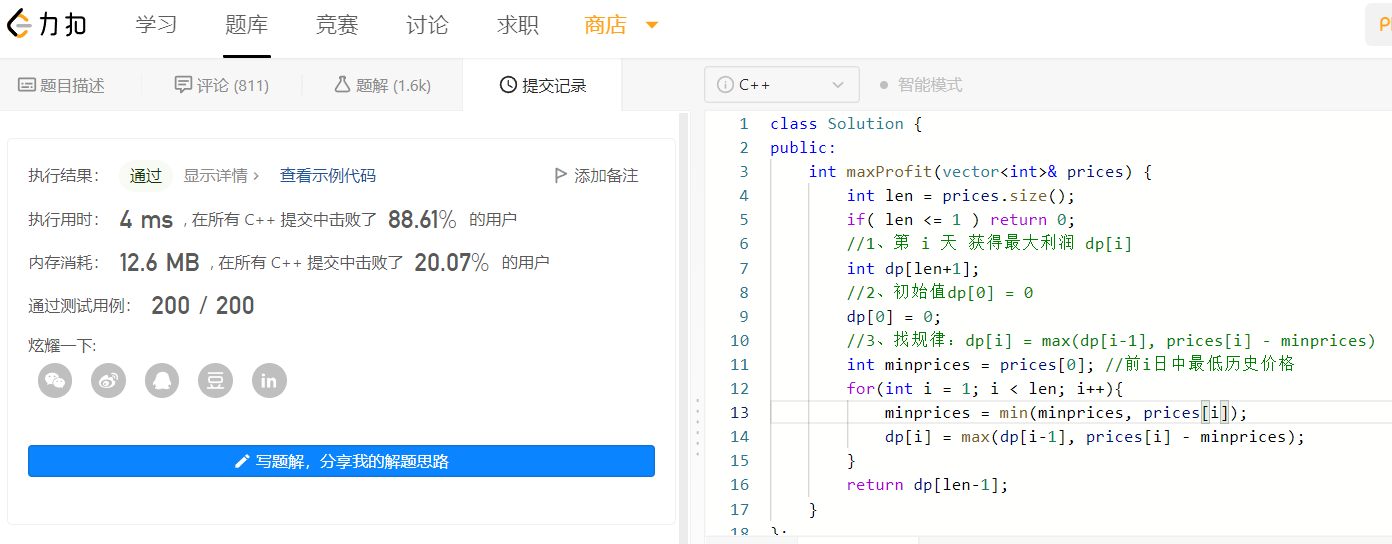
2、優雅的解決問題

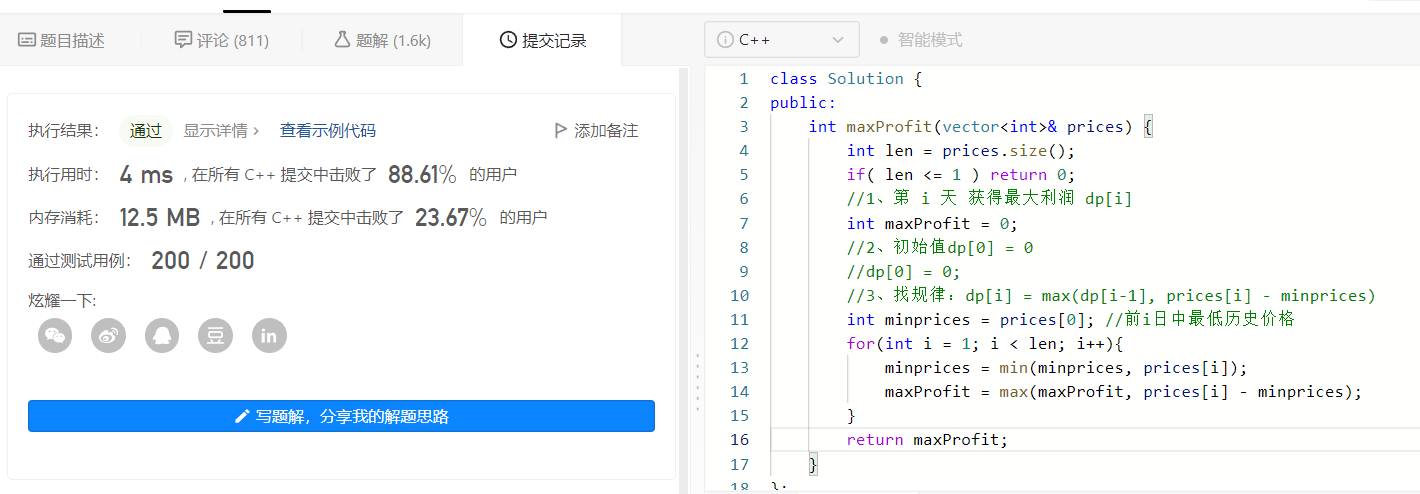
二、進階的二維DP

劍指offer47 禮物的最大價值

在一個 m*n 的棋盤的每一格都放有一個禮物，每個禮物都有一定的價值（價值大於 0）。你可以從棋盤的左上角開始拿格子裡的禮物，並每次向右或者向下移動一格、直到到達棋盤的右下角。給定一個棋盤及其上面的禮物的價值，請計算你最多能拿到多少價值的禮物？

範例 1:
輸入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
輸出: 12
解釋: 路徑 1→3→5→2→1 可以拿到最多價值的禮物

提示：
0 < grid.length <= 200
0 < grid[0].length <= 200

1、三板斧解決問題

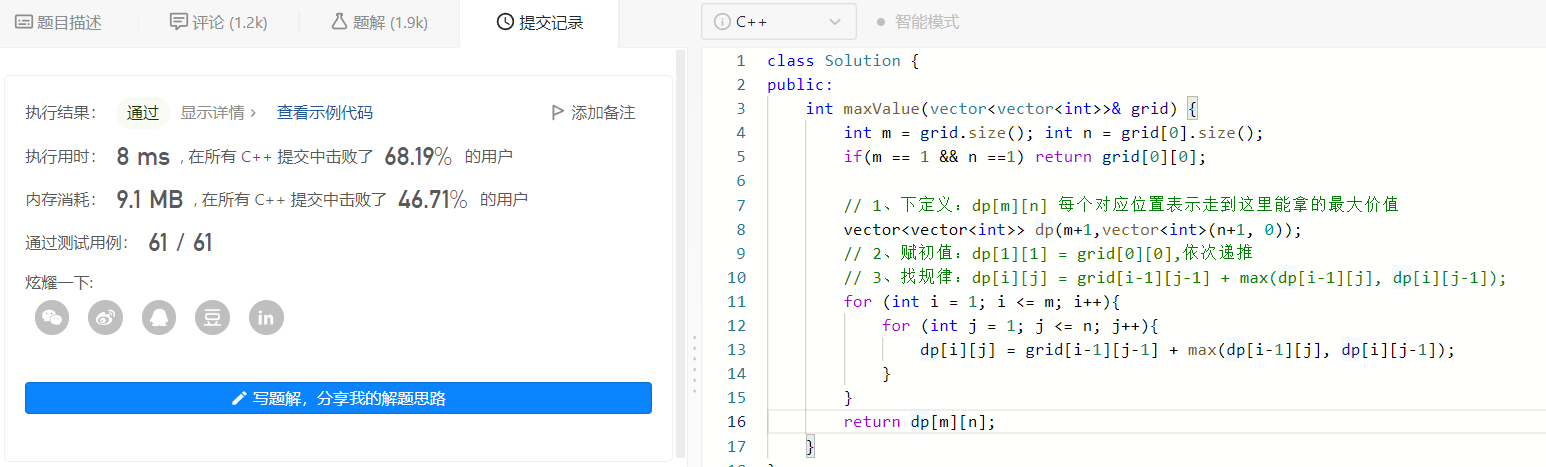
第一步： 下定義
首先必須知道最大價值的禮物一定是右下角的值，因為只能右或下移；
我們當然可以不用定義二維陣列，直接在源程式上修改，但是這樣毀壞了原始資料，所以我們新定義一個 dp[m+1][n+1] 的陣列來表示走到棋盤對應位置的已拿的最大價值；
第二步驟：定初值
每要求一個dp[i][j]位置的值，都需要dp[i][j-1]和dp[i-1][j]中的較大的值加上這個位置本身的值，所以dp[1][1] = grid[0][0]

第三步驟：找關係
每個位置的初值為當前位置的值，加上當前位置上一行的值和左邊的值中的較大值，因為當前位置的值只能是下移或者右移過來的；dp[i][j] = grid[i-1][j-1] + max(dp[i-1][j], dp[i][j-1]);
這裡發現賦初值的操作可以省略，因為推導的過程一起做了、最後返回推匯出的右下角的dp值就行；

注意：
1、下定義的時候如果是int dp[][]的形式要記得初始化每個元素為0，我這裡直接用的stl庫中的二維vector,下定義的同時初始化了每個元素為0；
2、如果不想下定義和定初值那麼麻煩，可以直接在grid 陣列上修改，先初始化第一列和第一行那麼就能直接從 1，1的位置開始推導，但是你心裡得明白推導的值的定義是什麼，初始化為啥這麼初始化

2、優雅的解決問題

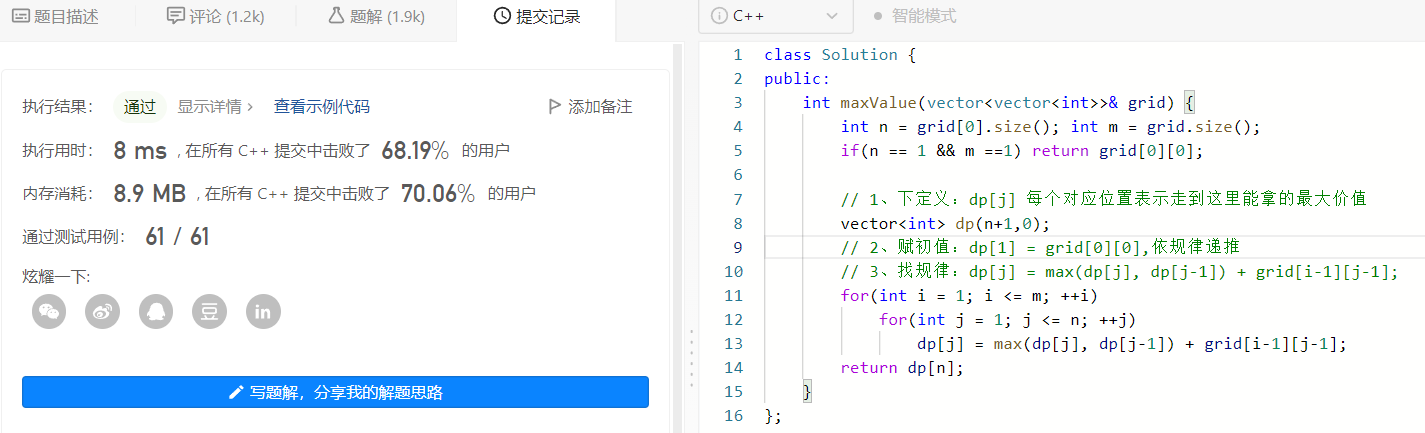
之前的一維dp中的優化問題把一維陣列降階為幾個變數，這裡我們把二維陣列降階為一維陣列，並用它來就像捲動一樣去遍歷下一個值，所以叫它捲動陣列。規律修改如下：
dp[j] = grid[i-1][j-1] + max(dp[j-1], dp[i-1]);
每次遍歷下一行陣列的值，新的dp[j]值為，舊的dp[j](當前元素的上邊元素)和dp[j-1](當前元素的左邊元素)中的最大值加上當前位置的禮物值；

可以這樣想象一下，從左到右從上到下遍歷每個位置的禮物的值的時候，有著一個捲動著的陣列每次都是在你要推導的值位置的上方，它記錄著假如走到捲動陣列中對應棋盤的位置所能拿到的禮物最大值。 而我每次要做的其實就是不斷更新捲動陣列中的值，讓它滾到最後一行即可；
需要注意的細節：
1、與三板斧解決問題的方法一樣，每次推導一個位置的值都需要當前位置左邊的值和上邊的值，我們用捲動陣列代替了這些值，不過三板斧時初始化是第一行和第一列置為0，這裡初始化是把卷動陣列置0；
2、注意陣列越界問題
3、思考一下為什麼不能再把卷動陣列降階成幾個變數表示（注意是不能修改原陣列，如果可以修改原陣列那麼可以不需要變數直接根據規律推導）

雖然三板斧也能解決問題，但是大部分情況下二維陣列的DP都可以優化為一維的DP，最主要的就是要找出它們之間的值依賴關係，也就是規律，就算是hard難度級別的題也是如此，比如下面這題

編輯距離

題目描述
給你兩個單詞 word1 和 word2， 請返回將 word1 轉換成 word2 所使用的最少運算元 。

你可以對一個單詞進行如下三種操作：

插入一個字元
刪除一個字元
替換一個字元

範例 1：
輸入：word1 = "horse", word2 = "ros"
輸出：3
解釋：
horse -> rorse (將 'h' 替換為 'r')
rorse -> rose (刪除 'r')
rose -> ros (刪除 'e')
範例 2：

輸入：word1 = "intention", word2 = "execution"
輸出：5
解釋：
intention -> inention (刪除 't')
inention -> enention (將 'i' 替換為 'e')
enention -> exention (將 'n' 替換為 'x')
exention -> exection (將 'n' 替換為 'c')
exection -> execution (插入 'u')

提示：
0 <= word1.length, word2.length <= 500
word1 和 word2 由小寫英文字母組成

1、三板斧解決問題

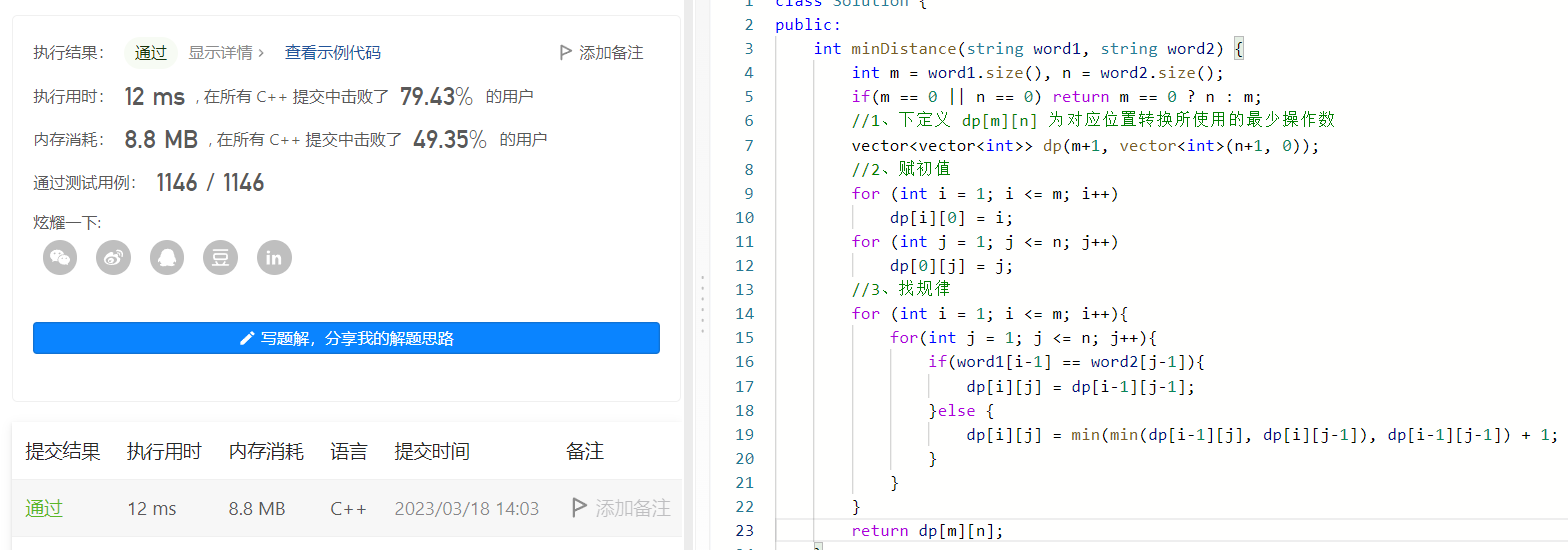
第一步： 下定義
要求將 word1 轉換成 word2 所使用的最少運算元，那麼就設 dp[m+1][n+1] 為 最少運算元
第二步驟：定初值
初值怎麼定？看題目啊！！！重要得事情說三遍

解釋範例	空	r	o	s
空	從空到空為0	從空到r 為 1	從空到 ro 為 2	從空到 ro 為 3
h	從h到空為 1	-----	-----	-----
o	從ho到 空 為2	-----	-----	-----
r	從hor到 空為 3	-----	-----	-----
s	-----	-----	-----	-----
e	-----	-----	-----	-----

看一下題目最簡單的例子，很輕鬆的初值怎麼賦值我就不多說了吧（實在是懶得敲完,直接電腦跑出來看）

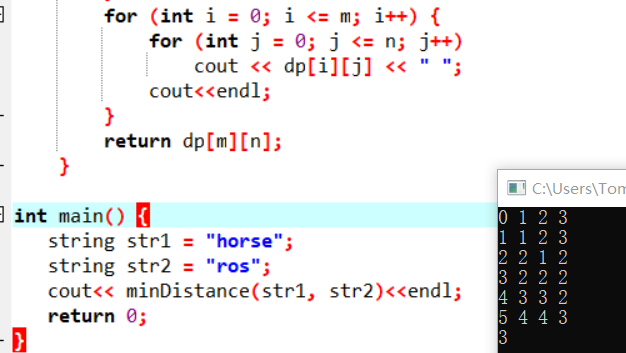
第三步驟：找關係
通過例子找規律，通過簡單的推複雜的，觀察一下子例子如下（省略了無用數值）：

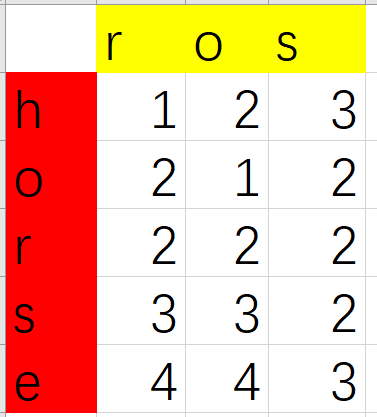
可以發現這樣一種規律：
當word1[i-1] == word2[j-1] 時， dp[i][j] = dp[i-1][j-1]
當word1[i-1] != word2[j-1] 時， dp[i][j] = min( dp[i-1][j-1], dp[i-1][j] , dp[i][j-1] ) + 1

根據這個規律敲完程式碼就Ok了,當然了這個規律得推導過程是繁瑣而漫長的，不然怎麼會有一杯茶一隻煙，一個題目做一天的說法

2、優雅的解決問題

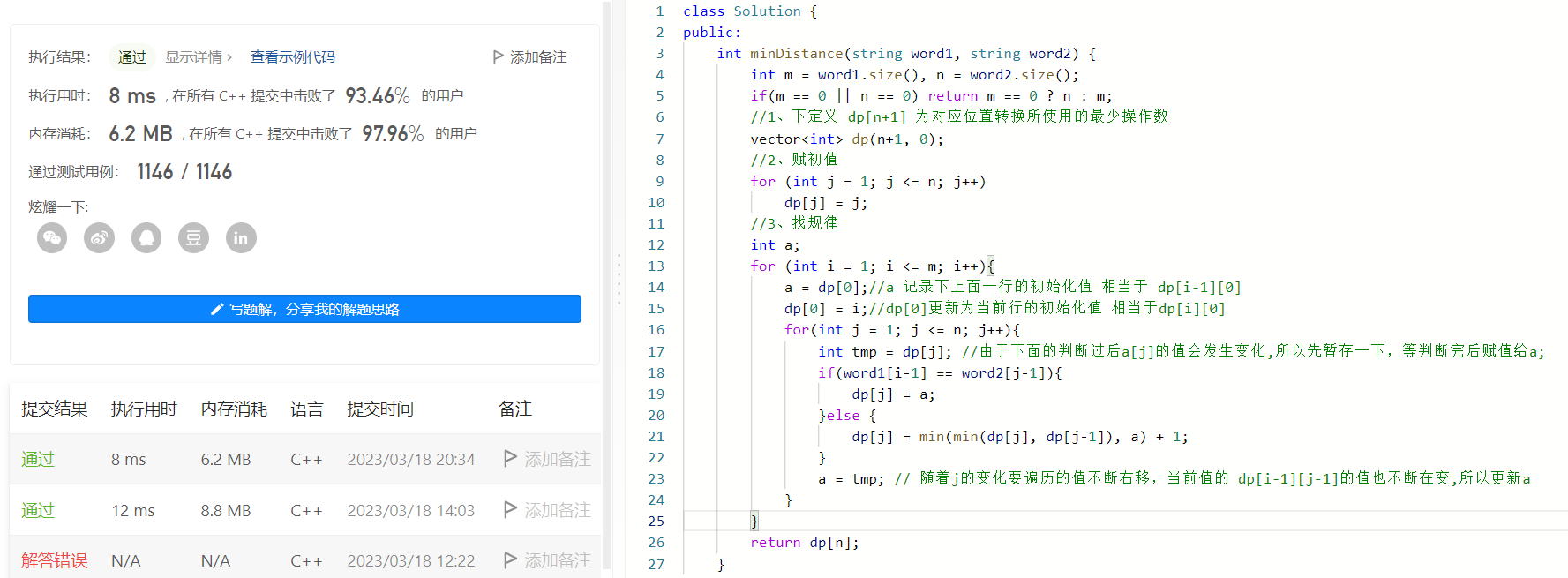
多數二維dp都可以降階為一維dp這裡也不例外，這裡的降級和前面禮物的最大價值差不多也是用捲動陣列，區別在於禮物的最大價值每次推導只用上、左兩變數就行，而這裡需要左上，上，左三變數；所以多出來的左上用a來表示，它其實就是之前的dp[i-1][j-1],然後就是要隨著每一行的往右去的推導不斷變化值；

注意：由於每次推導方程要用到a，而a用完以後需要更改為下一個值的dp[i-1][j-1] 也就是d[j]的原始值，但是d[j]發生了變化，所以先用個tmp存一下,推導完後賦值給a；

三、文末

演演算法之道，無窮無盡也，求解之道，無他，唯手熟爾！ 遇到需要求什麼最優，最值之類的題目且元素之間存在規律或者說聯絡的題目時，你應該要想的到動態規劃，然後這解題三板斧下去，至少能開個頭，接著就是靠簡單的案例入手去找規律了，大部分情況下不是一維dp就是二維dp，先別管怎麼優化做出來能把用例跑通再說優化，接著就是考慮一些細節上的問題。 以上大概就是最近所領悟的經驗，如果有問題歡迎指出來評論交流，如果感覺有用的話別忘了給個贊，讓我知道能夠給別人帶來了一點點的啟發，那我就已經非常開心了。

ps ： 關鍵在於多練哦，編輯距離這道題我起碼寫了3遍以上才能夠獨立寫出來，最初看題解都是懵逼的，主要是那個規律你想要去推出來要麼是你刷過類似的題目有經驗，要不然就是真的天分比較好邏輯能力很強的大佬能夠自己獨立的把它推匯出來，否則第一次誰都很難說把它做出來，所以不要灰心，你做一次不行，那就兩次，過段時間忘了在像我一樣第三次，第四次這樣的話就可以躋身前者，之後碰到類似的也就不怕了，前進吧，少年，0和1的世界還有很多的未知等待著你，沖沖衝！！！