【資料結構與演演算法學習】雜湊表（Hash Table，雜湊表）

實現語言：C++

1. 雜湊表

雜湊表，英文名稱為Hash Table，又稱雜湊表、雜湊表等。

線性表和樹表的查詢是通過比較關鍵字的方法，查詢的效率取決於關鍵字的比較次數。

而雜湊表是根據關鍵字直接存取的資料結構。雜湊表通過雜湊函數將關鍵字對映到儲存地址，建立了關鍵字和儲存地址之間的一種直接對映關係。

例如：關鍵字集key = (17, 24, 48, 25)，雜湊函數H(key) = key % 5，雜湊函數將關鍵字對映到儲存地址下標，將關鍵字儲存到雜湊表的對應位置。

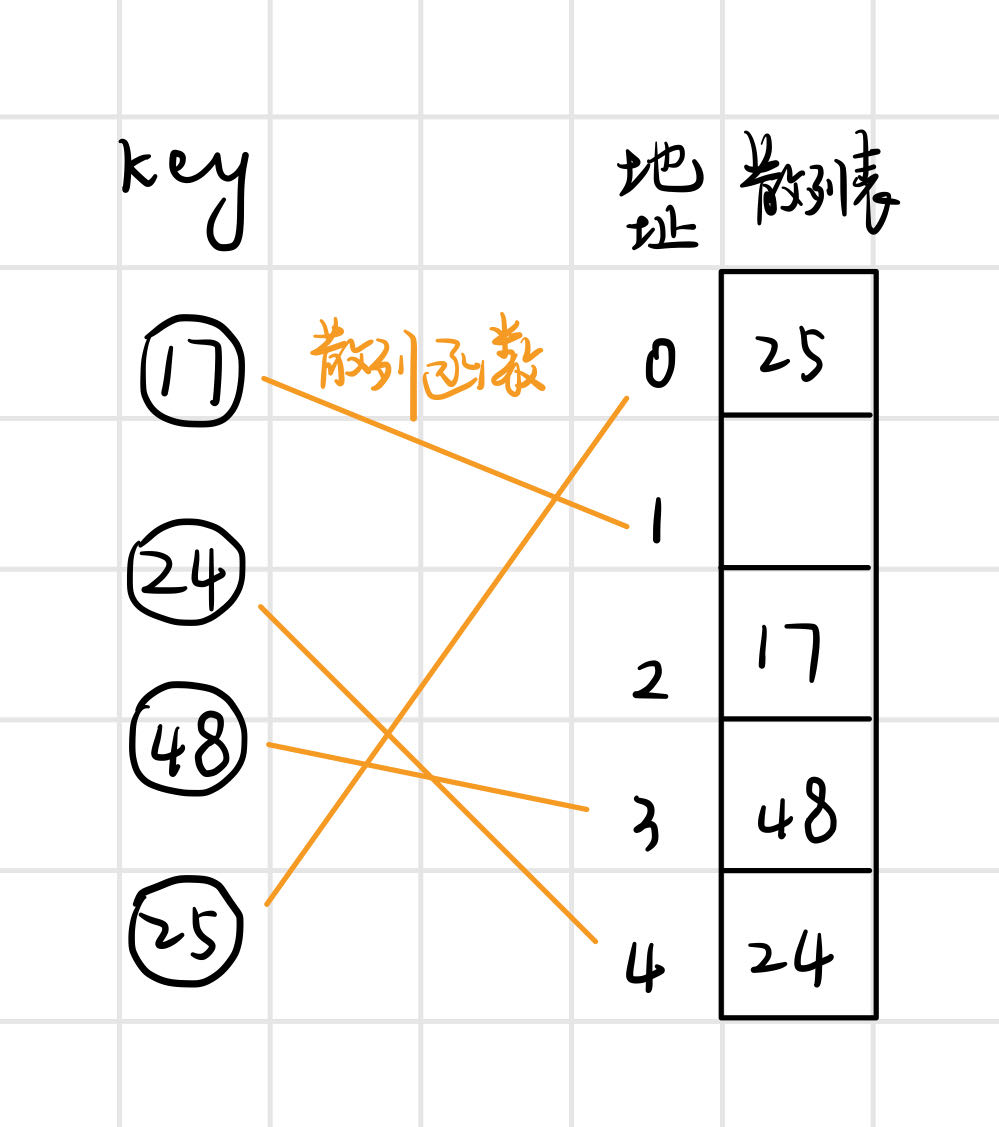
理想情況下，雜湊表查詢的時間複雜度是O(1)。但是，雜湊函數可能會把兩個或兩個以上的關鍵字對映到同一地址，發生「衝突」，發生衝突的不同關鍵字稱為「同義詞」，也就是具有相同函數值的關鍵字。

接上例，如果13也要存入雜湊表，就會和48產生衝突：

所以，使用雜湊表需要解決好兩個問題：構造合適的雜湊函數，以及制定一個好的解決衝突的方案。

2. 雜湊函數的構造方法

在構造雜湊函數時需要考慮諸多因素：執行速度、關鍵字長度、雜湊表大小、關鍵字的分佈情況、查詢頻率等。

根據元素集合的特性構造，我們對雜湊函數有以下要求：

1. n的資料來源僅佔n個地址，雖然雜湊查詢是以空間換時間，但仍希望雜湊的地址空間儘量小。
2. 無論用什麼方法儲存，目的都是儘量均勻地存放元素，以避免衝突。

常見的構造方法有：直接定址法、除留餘數法、數位分析法、平方取中法、摺疊法、亂數法。

2.1 直接定址法

以關鍵碼key的某個線性函數值作為雜湊地址

　　Hash(key) = a * key + b  (a，b為常數)

優點是線性關係，不會產生衝突。但是要佔用連續的地址空間，空間效率低下。

適合查詢表較小且連續的情況。

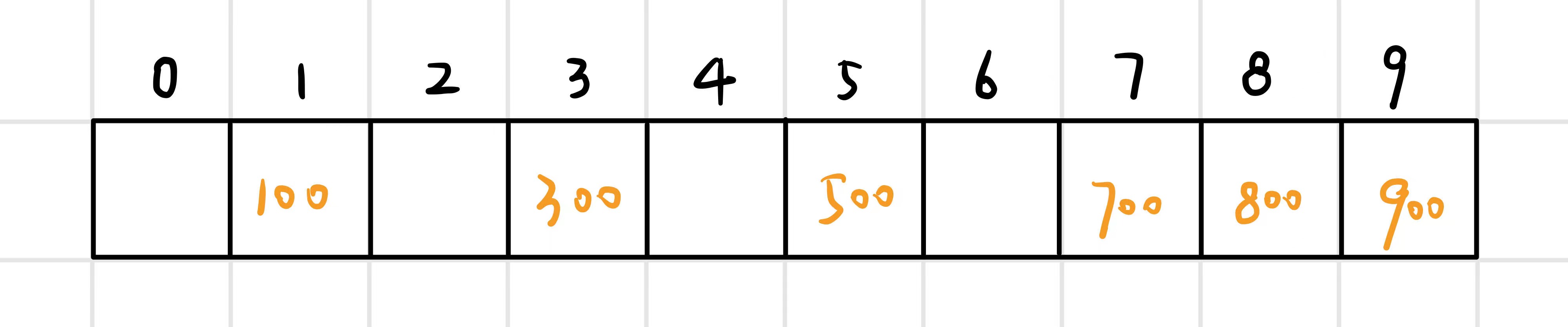
例如：使用直接定址法儲存序列 {100, 300, 500, 700, 800, 900}，選擇雜湊函數 Hash(key) = key / 100  (a=1/100, b=0)

2.2 除留餘數法

此方法是最常用的雜湊函數構造方法

　　Hash(key) = key mod p   (p是一個整數)

關鍵：如何選取合適的p?

技巧：設表長為m，取p≤m，且p為質數

例：{15, 23, 27, 38, 53, 61, 70}，雜湊函數 Hash(key) = key mod 7

2.3 數位分析法

如果關鍵字是位數較多的數位（比如手機號），且這些數位部分存在相同規律，則可以採用抽取剩餘不同規律部分作為雜湊地址。

比如手機號前三位是接入號，中間四位是 HLR 識別號，只有後四位才是真正的使用者號。也就是說，如果手機號作為關鍵字，那麼極有可能前 7 位是相同的，此時我們選擇後四位作為雜湊地址就是不錯的選擇。同時，對於抽取出來的數位，還可以再進行反轉、右環位移、左環位移等操作，目的就是為了提供一個能夠儘量合理地將關鍵字分配到雜湊表的各個位置的雜湊函數。

數位分析法通常適合處理關鍵字位數比較大的情況，如果事先知道關鍵字的分佈且關鍵字的若干位分佈較均勻，就可以考慮用這個方法。

2.4 平方取中法

以關鍵字平方的中間位數作為雜湊地址。

比如假設關鍵字是 4321，那麼它的平方就是 18671041，抽取中間的 3 位就可以是 671，也可以是 710，用做雜湊地址。

適合於不知道關鍵字的分佈，而位數又不是很大的情況。

2.5 摺疊法

摺疊法是將關鍵字從左到右分割成位數相等的幾部分（注意最後一部分位數不夠時可以短些），然後將這幾部分疊加求和，並按雜湊表表長，取後幾位作為雜湊地址。

比如假設關鍵字是 9876543210，雜湊表表長為三位。

有時可能這還不能夠保證分佈均勻，那麼也可以嘗試從一端到另一端來回摺疊後對齊相加，比如將 987 和 321 反轉，再與 654 和 0 相加，變成 789+654+123+0=1566，此時雜湊地址為 566。

摺疊法事先不需要知道關鍵字的分佈，適合關鍵字位數較多的情況。

2.6 亂數法

選擇一個亂數，取關鍵字的隨機函數值作為它的雜湊地址：

　　hash(key) = random(key)

當關鍵字的長度不等時採用這個方法構造雜湊函數是比較適合的。

3. 處理雜湊衝突的方法

3.1 開放定址法（開地址法）

基本思想：有衝突時就去尋找下一個空的雜湊地址，只要雜湊表足夠大，空的雜湊地址總能找到，並將資料元素存入。

常用的開放定址法有線性探測法、二次探測法、偽隨機探測法等。

3.1.1 線性探測法

　　Hi = (Hash(key) + di) mod m，（1 ≤ i ≤ m）

其中，m為雜湊表長度，di = i（i為1,2，...，m-1 線性序列）

例：關鍵碼集為{47, 7, 29, 11, 16, 92, 22, 8, 3}，雜湊表長度為m=11，雜湊函數為Hash(key)=key mod 11，使用線性探測法處理衝突，存入過程如下：

3.1.2 二次探測法

　　增量序列di為1²，-1²，2²，-2²，...，q² 二次序列

同樣是上邊的例子，使用二次探測法處理衝突，存入過程如下：

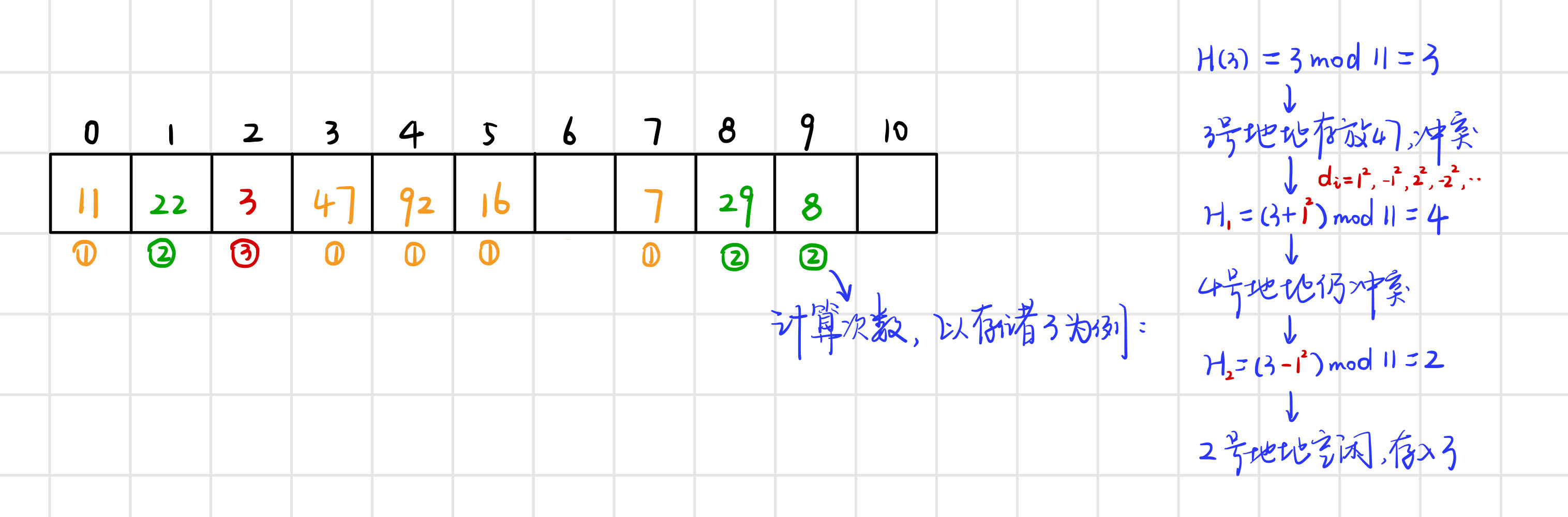
注意：二次探測法是跳躍式探測，效率較高，但是會出現命名有有空間卻探測不到的情況，因而儲存失敗，而線性探測只要有空間就一定能探測到。

3.1.3 偽隨機探測法

　　增量序列di為偽亂數

其存入原理和上邊兩種方法一致，這裡不多做介紹。

3.2 鏈地址法（拉鍊法）

基本思想：將相同雜湊地址的記錄（即同義詞）鏈成一單連結串列。

m個雜湊地址就是m個單連結串列，然後用一個陣列將m個單連結串列的表頭指標儲存起來，形成一個動態的結構。

例如：關鍵字為{19, 14, 23, 1, 68, 20, 84, 27, 55, 11, 10, 79}，雜湊函數為Hash(key) = key mod 13，使用鏈地址法儲存如下所示：

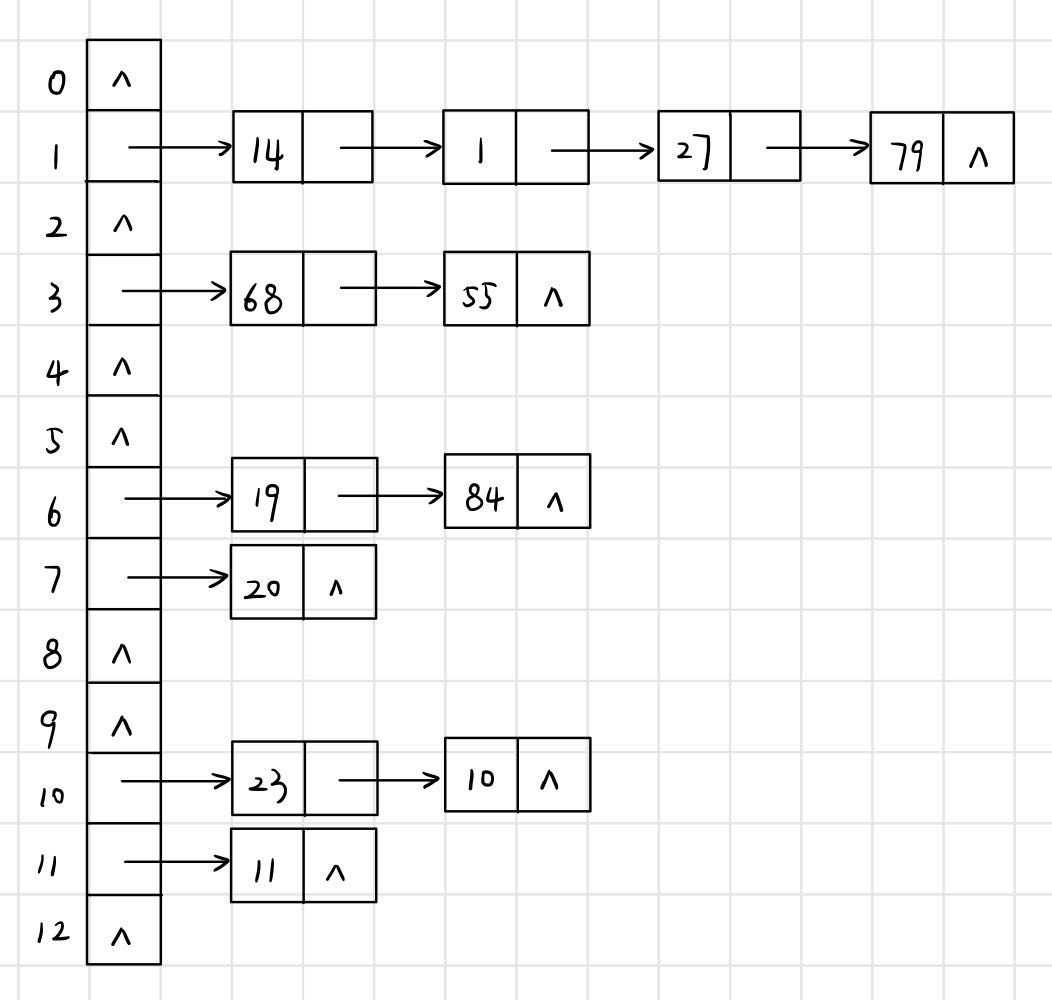
鏈地址法建立雜湊表的步驟：

1. 取陣列元素的關鍵字key，計算其雜湊函數值（地址）。若該地址對應的連結串列為空，則將該元素插入此連結串列；否則執行下一步解決衝突；
2. 根據選擇的衝突處理方式，計算關鍵字key的下一個儲存地址。若改地址對應的連結串列不為空，則利用連結串列的前插法或後插法將該元素插入此連結串列。

優點：

1. 非同義詞（同義詞是指具有相同函數值的關鍵字）不會衝突，無「聚集」現象；
2. 連結串列上結點空間動態申請，更適合於表長不確定的情況

3.3 再雜湊法

3.4 建立一個公共溢位區

將雜湊表分為公共表和溢位表，當溢位發生時，將所有溢位資料統一存放到溢位區。

4. 雜湊表的查詢

給定查詢值k，查詢過程如圖所示：

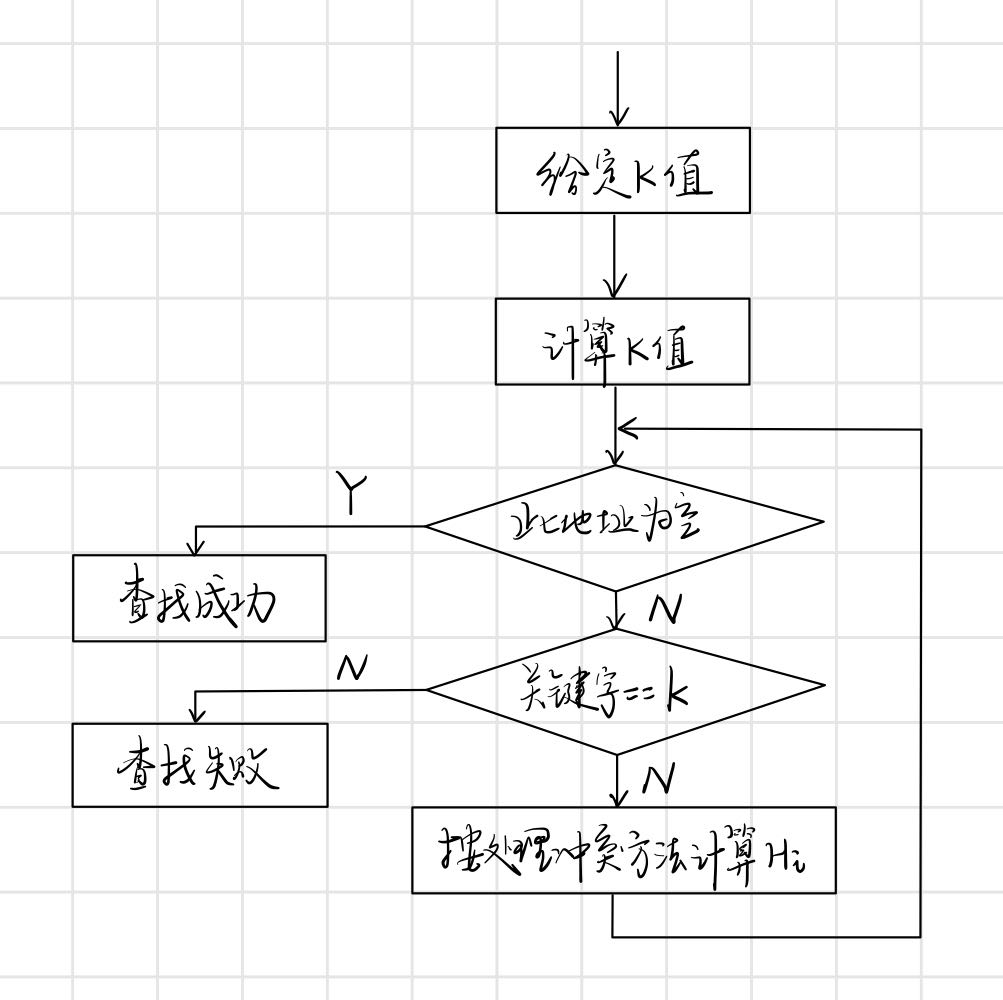
雜湊表的查詢效率分析

一般我們使用平均查詢長度ASL來衡量查詢效率，雜湊表ASL的值取決於：雜湊函數、處理衝突的方法、雜湊表的裝填因子α（α = 表中填入的記錄數 / 雜湊表的長度，α越大，表中記錄數越多，發生衝突的可能性就越大，查詢對比次數就越多）。

　　線性探測法：ASL ≈  1 / 2 * (1 + 1 / (1 - α))

　　拉鍊法：ASL ≈ 1 + α / 2

　　隨機探測法：ASL ≈ -1 / α * ln(1 - α)

例：對於關鍵字集{19, 14, 23, 1, 68, 20, 84, 27, 55, 11, 10, 79}，n=12，雜湊函數為：H(key) = key mod 13，雜湊表表長為m = 16，設每個記錄的查詢概率相等。則使用不同查詢演演算法的平均查詢效率如下：

　　線性探測法：ASL ≈ 1 / 2 * (1 + 1 / (1 - 0.75)) = 2.5   (裝填因子α = n / m = 0.75)

　　拉鍊法：ASL ≈ 1 + 0.75 / 2 = 1.375

　　隨機探測法：ASL ≈ -1 / α * ln(1 - α) = 1.85

對比無序表查詢和有序表折半查詢：

　　無序表：ASL = (n +1) / 2 = 6.5

　　有序表折半查詢：ASL = lg₂(n + 1) - 1 = 2.7

總結以下幾點：

1. 雜湊表技術具有很好的平均效能；
2. 鏈地址法優於開地址法；
3. 除留取餘法做雜湊函數優於其它型別函數。

C++程式碼

#include <iostream>
#include <cstring>

using namespace std;

#define m 15	// 雜湊表的表長
#define NULLKEY 0	// 單元為空的標記

int HT[m], HC[m];

// 雜湊函數
int H(int key) {
	return key % 13;
}

// 線性探測
int LineDetect(int HT[], int H0, int key, int& cnt) {
	int Hi;
	for (int i = 0; i < m; i++) {
		cnt++;
		Hi = (H0 + i) % m;	// 按照線性探測法計算下一個雜湊地址Hi
		if (HT[Hi] == NULLKEY || HT[Hi] == key)
			return Hi;		// 若單元Hi為空，則所查元素不存在		
	}
	return -1;
}

// 二次探測
int SecondDetect(int HT[], int H0, int key, int& cnt) {
	int Hi;
	for (int i = 1; i <= m / 2; ++i) {
		int i1 = 1 * i;
		int i2 = -i1;
		cnt++;
		Hi = (H0 + i1) % m;	// 按照二次探測法去計算下一個雜湊地址
		if (HT[Hi] == NULLKEY || HT[Hi] == key)	// 若單元Hi為空或者查詢成功
			return Hi;
		cnt++;
		Hi = (H0 + i2) % m;	// 按照二次探測法去計算下一個雜湊地址
		if (Hi < 0)
			Hi += m;
		if (HT[Hi] == NULLKEY || HT[Hi] == key)	// 若單元Hi為空或者查詢成功
			return Hi;
	}
	return -1;
}

// 雜湊表中查詢關鍵字key
void SearchHash(int HT[], int key) {
	int H0 = H(key);	// 計算雜湊地址
	int Hi, cnt = 1;
	if (HT[H0] == NULLKEY)
		cout << "查詢失敗" << endl;
	else if (HT[H0] == key)
		cout << "查詢成功。" << "在第" << H0 + 1 << "位置。" << "比較次數：" << cnt << endl;
	else {
		Hi = LineDetect(HT, H0, key, cnt);
		// Hi = SecondDetect(HT, H0, key, cnt);
		if (HT[Hi] == key)
			cout << "查詢成功。" << "在第" << H0 + 1 << "位置。" << "比較次數：" << cnt << endl;
		else
			cout << "查詢失敗。比較次數：" << cnt << endl;
	}
}

// 插入元素
bool InsertHash(int HT[], int key) {
	int H0 = H(key);	// 根據雜湊函數H(key)計算雜湊地址
	int Hi, cnt = 1;
	if (HT[H0] == NULLKEY) {
		HC[H0] = 1;		// 統計比較次數
		HT[H0] = key;	// 放入H0中
		return 0;
	}
	else {
		Hi = LineDetect(HT, H0, key, cnt);
		// Hi = SecondDetect(HT, H0, key, cnt);
		if (Hi != -1 && HT[Hi] == NULLKEY) {
			HC[Hi] = cnt;	// 統計比較次數
			HT[Hi] = key;	// 放入H0中
			return 1;
		}
	}
	return 0;
}

void print(int HT[]) {
	for (int i = 0; i < m; i++)
		cout << HT[i] << "\t";
	cout << endl;
}

int main() {
	int x;
	memset(HT, 0, sizeof(HT));
	memset(HC, 0, sizeof(HC));
	print(HT);
	cout << "輸出12個關鍵字，存入雜湊表中：" << endl;

	for (int i = 0; i < 12; i++) {
		cin >> x;
		if (!InsertHash(HT, x)) {
			cout << "建立雜湊表失敗！" << endl;
			return 0;
		}
	}
	cout << "輸出雜湊表：" << endl;
	print(HT);
	print(HC);
	cout << "輸入要查詢的關鍵字" << endl;
	cin >> x;
	SearchHash(HT, x);
	return 0;
}

// 測試資料1：14 36 42 38 40 15 19 12 51 68 34 25
// 測試資料2：14 36 42 38 40 15 19 12 51 68 34 18

參考資料

1. 資料結構與演演算法基礎（青島大學王卓）

2. 資料結構—— 構造雜湊函數的六種方法【直接定址法-數位分析法-平方取中法-摺疊法-除留餘數法-亂數法】

3. 雜湊衝突常用解決方法

4. 書籍：演演算法訓練營