The art of being wise is the art of knowing what to overlook .
智慧的藝術是知道該忽視什麼。

——威廉·詹姆斯（William James）

1 導引

1.1 跨域推薦簡介

推薦系統中常常面臨使用者冷啟動問題^[1]，也即新註冊的使用者沒有足夠的互動記錄，導致推薦模型不能學習到有效的表徵。為了解決使用者冷啟動問題，近年來跨域推薦（CDR） 得到了許多關注^[2]。一般來講，跨域推薦旨在利用從其它相關源域收集的使用者-物品互動資訊以提升目標域的推薦質量。許多跨域推薦的工作會假設大量的使用者在兩個域都出現過（即重疊使用者, overlapping users）以搭建起源域和目標域之間的橋樑。只在源域中存在的使用者（即非重疊使用者, non overlapping users）可以被視為目標域的冷啟動使用者。

1.2 嵌入和對映的思路

為了解決冷啟動使用者問題，傳統的跨域推薦方法常常基於嵌入和對映（Embedding and Mapping，EMCDR） 的思路，也即學習一個對映函數將預訓練的使用者表徵（embeddings）從源域遷移到目標域。如下圖所示：

如上圖所示，EMCDR首先用基於協同過濾的模型（CF-based model）來為每個領域生成使用者/物品表徵，之後訓練一個對映函數來將源域和目標域的重疊使用者表徵。然後，再給定源域的非重疊冷啟動使用者表徵，就能夠根據訓練好的對映函數來預測目標域的使用者表徵了，之後再用於目標域的物品推薦。

然而，正如我們上面所說的，這種方法在進行對齊操作之前，各領域需要先通過預訓練以獨立地得到使用者/物品的embeddings。因此，有偏的（biased） 預訓練表徵將無可避免地包含領域特有的（domain-specific） 資訊，從而會導致對跨領域遷移資訊產生負面影響。

事實上，跨域推薦的關鍵問題就在於：究竟需要在不同的域之間共用什麼資訊？也即如何讓表徵能夠編碼到領域間共用(domain-shared)的資訊？

1.3 聯合訓練的思路

這種思路相比於EMCDR方法的優點在於，我們能夠聯合（jointly）學習跨領域的embeddings，從而能夠進一步地關注於領域共用資訊並限制領域特有的資訊。

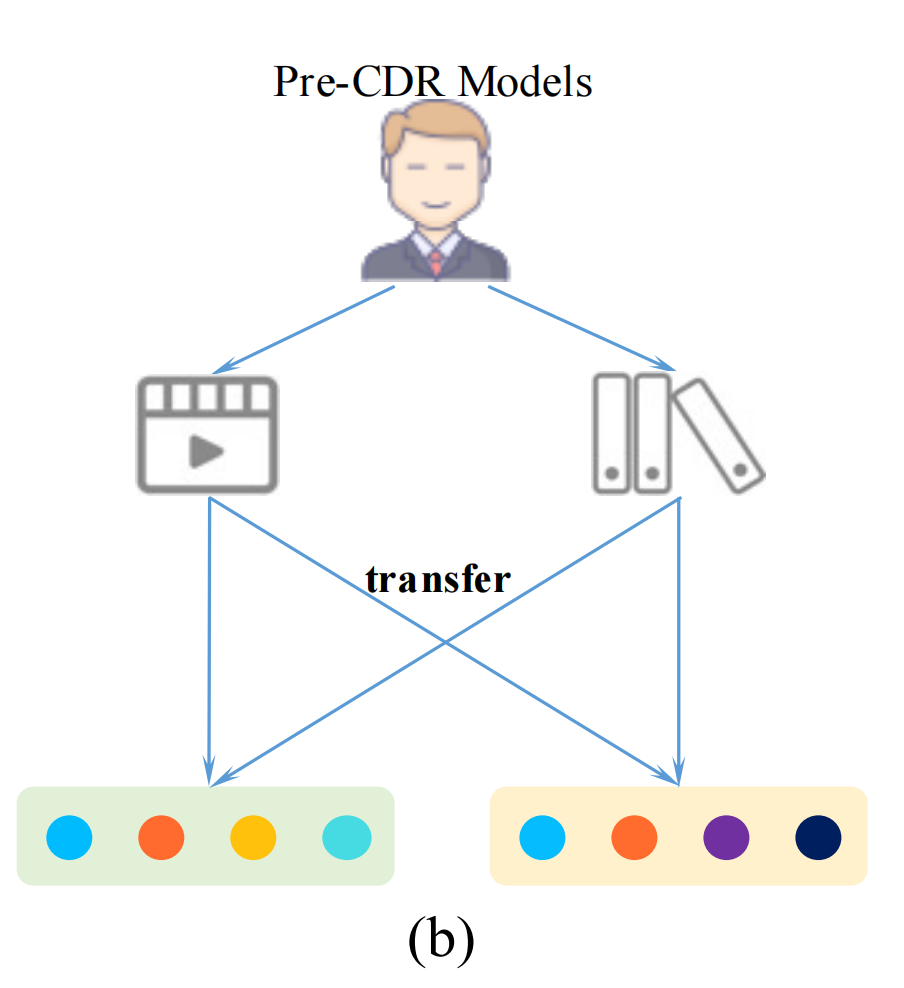
在具體的手段層面，這種方法該類方法的大多數工作首先採用兩個基礎的編碼器來對每個領域的互動記錄建模，之後再引入不同的遷移層來對稱地融合不同編碼器學得的表徵。比如，CoNet^[3]利用MLP做為每個領域的基礎編碼器，並設計了交叉連線（cross-connections）網路來遷移資訊。DDTCDR^[4]進一步擴充套件了ConNet:學習了一個潛在的正交投影函數來遷移跨領域使用者的相似度。PPGN^[5]使用堆疊的（stacking）GCN來直接聚合來自各領域的表徵資訊以學得使用者/物品表徵。BiTGCF^[6]利用LightGCN^[7]做為編碼器來聚合每個領域的互動資訊，並進一步引入特徵遷移層來增強兩個基礎的圖編碼器。CDRIB^[8]則採用資訊瓶頸的視角來獲得領域間共用的資訊（不過該方法關注的是為目標域中的不重疊（冷啟動）使用者做推薦，與前面的方法又有所區別）。

1.4 解耦表徵的思路

儘管以上的方法在一定程度上有效，但它們基本上仍然忽略了對領域共用資訊和領域特有資訊的解耦（CDRIB除外），而這大大限制了模型遷移的效率。

一個顯著的例子如上圖所示。對於Film和Book這兩個領域，領域間共用的資訊，比如「Story Topic」和「Category」能夠為每個領域都提供有價值的資訊。但領域特有的資訊，比如Book領域的「Writing Style」可能會提供對於在「Film」領域做推薦無用的資訊甚至會導致CDR領域的負遷移現象^[9]。不幸的是，現有的CDR方法忽視了此問題並直接聚合領域間共用和領域特有的資訊。這樣的結果就是，學得的使用者表徵將不同領域的偏好糾纏（entangle）在一起，而這會導致獲得次優（sub-optial）的推薦結果。

解決該問題的手段是解耦領域間共用的領域特有的表徵，其代表為DisenCDR模型^[10]。

如上圖所示，DisenCDR模型將領域共用的和領域特有的表徵進行解耦，以達到跨領域知識遷移的目的。

2 論文閱讀

2.1 ICDE 2022《Cross-Domain Recommendation to Cold-Start Users via Variational Information Bottleneck》^[8]

本方法屬於採用聯合訓練的跨域推薦方法。本其關注的場景為當源域和目標域間的使用者部分重疊時，為目標域中的不重疊（冷啟動）使用者做推薦。該方法所要解決的問題在於，究竟有哪些資訊需要在領域間進行共用？

為了解決該問題，本文利用了資訊瓶頸（information bottleneck）原理並提出了一個新的方法（CDIRB模型）來使表徵編碼到領域間共用的資訊（domain shared information），從而用於各領域的下游推薦。為了得到無偏的表徵，作者設計了兩種正則項，其中資訊瓶頸正則項來同時建模跨域/域間的使用者-物品互動，這樣相比EMCDR方法，就能夠同時考慮所有域的互動資訊從而達到去偏的目的；而對比資訊正則項則負責捕捉跨域的使用者-使用者之間的關係（對齊不同域之間的重疊使用者表徵）。

設有領域\(X\)和\(Y\)，設\(D^X=(\mathcal{U}^X, \mathcal{V}^X,\mathcal{E}^X)\)，\(D^Y=(\mathcal{U}^X, \mathcal{V}^X,\mathcal{E}^X)\)表示領域的資料，這裡\(\mathcal{U}\)、\(\mathcal{V}\)、\(\mathcal{E}\)分別表示每個領域使用者、物品和邊的集合。特別地，使用者集合\(\mathcal{U}^X\)和\(\mathcal{U}^Y\)包含重疊的使用者子集\(\mathcal{U}^o = \mathcal{U}^X \cap \mathcal{U}^Y\)。接著，使用者集合可以被形式化為\(\mathcal{U}^X = \{\mathcal{U}^x, \mathcal{U}^o\}\)和\(\mathcal{U}^Y = \{\mathcal{U}^y, \mathcal{U}^o\}\)，這裡\(\mathcal{U}^x\)和\(\mathcal{U}^y\)為在每個領域中不重疊的使用者集合。設\(\boldsymbol{A}^X=\{0,1\}^{\left|\mathcal{U}^X\right| \times\left|\mathcal{V}^X\right|}\)和\(A^Y=\{0,1\}^{\left|\mathcal{U}^Y\right| \times\left|\mathcal{V}^Y\right|}\)為儲存使用者-物品互動資訊的兩個二值矩陣。這樣，本文的任務可形式化地描述為：給定來自源域\(X\)的非重疊的（冷啟動）使用者\(u_i\in \mathcal{U}^x\)，我們想要為其推薦來自目標域\(Y\)的物品\(v_j \in \mathcal{V}^Y\)（或為來自\(\mathcal{U}^y\)的使用者推薦來自\(\mathcal{V}^X\)的物品）。

接下來作者借鑑了論文^[11][12]提出的資訊瓶頸理論，該理論旨在學習有效表徵，這種有效表徵能夠在簡潔性和廣泛的預測能力之間做權衡（trade-off）^[13]。形式化地，標準資訊瓶頸有如下所示的目標函數：

該目標函數可以被解釋為兩部分：（1）最小化\(I(Z; X)\)旨在懲罰\(Z\)和\(X\)之間的互資訊，也即使得\(Z\)儘量「忘掉」\(X\)的資訊。(2) 最大化\(I(Z; Y)\)則鼓勵\(Z\)去預測\(Y\)。綜合來看，資訊瓶頸原理的目標為壓縮\(X\)以得到表徵\(Z\)，該表徵能夠去除掉對預測\(Y\)無用的因素而保留相關因素^[14]。這也就是說IB使得\(Z\)做為一個最小充分統計量^[15]（在我們這個CDR應用中即領域間應該共用的資訊）。在實踐中，直接優化互資訊是難解（intractable）的，因此變分近似^[16]常常用於構建用於優化互資訊目標函數的下界^[13][17]。

本文提出的CDIRB模型包含變分子圖編碼器（variational bipartite graph encoder，VBGE）和兩種的跨領域資訊正則項，整體框架圖如下圖所示：

其中綠色部分的網格代表物品表徵，黃色和藍色顏色的網格分別代表重疊和不重疊的使用者表徵。資訊瓶頸正則項（圖中的Information Bottleneck）捕捉了領域間使用者和物品的相關性，而對比資訊正則項（圖中的Contrastive Information）則捕捉了領域間重疊使用者之間的相關性。

接下來我們敘述每個部分的細節。

嵌入層

嵌入層得到的領域\(X\)的使用者/物品表徵分別記作\(\boldsymbol{U}^X \in \mathbb{R}^{|\mathcal{U}^X |\times F}\)和\(\boldsymbol{V}^X \in \mathbb{R}^{\left|\mathcal{V}^X\right| \times F}\)；領域\(Y\)的使用者/物品表徵分別記作\(\boldsymbol{U}^Y \in \mathbb{R}^{\left|\mathcal{U}^{Y}\right| \times F}\)和\(\boldsymbol{V}^Y \in \mathbb{R}^{\left|\mathcal{V}^Y\right| \times F}\)。

變分二分圖編碼器
為了在原始使用者/物品表徵的基礎上，進一步提煉出使用者/物品的隱向量表徵，論文提出了變分二分圖編碼器（VBGE）。比如，生成\(X\)領域的使用者隱向量表徵\(Z_v^X\)的過程如下：

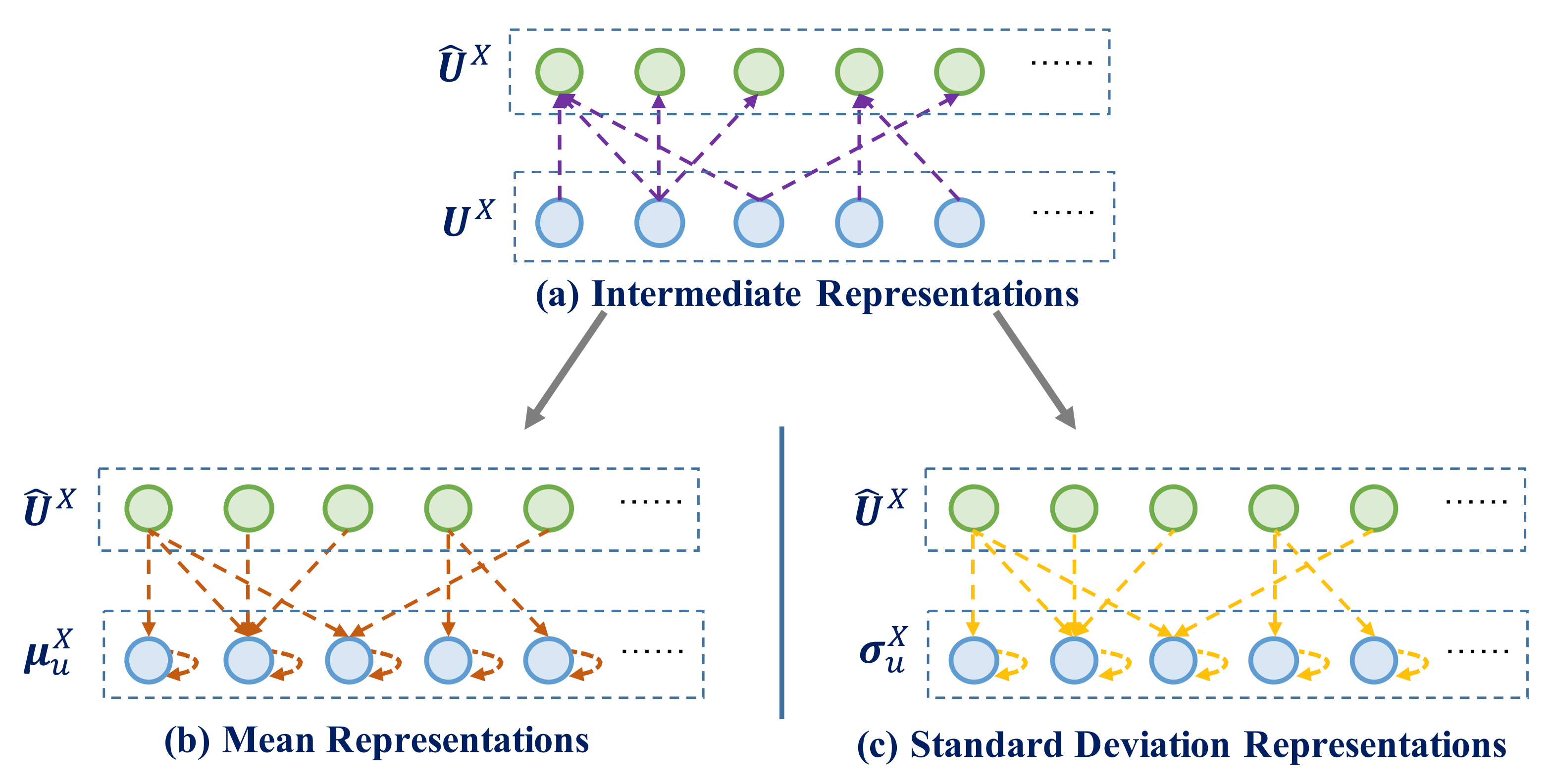
資訊瓶頸正則項

接下來，論文引入了資訊瓶頸正則項和對比資訊正則項這兩種正則項來捕捉領域間的相關性，以學得包含領域間共用資訊的無偏表徵。其中資訊瓶頸正則化項旨在捕捉領域間使用者和物品間的相關性，而對比資訊正則化項旨在捕捉領域間的重疊使用者和使用者之間的相關性。

設\(\mathbf{X}\)，\(\mathbf{X}^u\)，\(\mathbf{X}^v\)分別為領域\(X\)中所觀測到的互動資訊、使用者資訊和物品資訊。領域\(X\)的使用者集合包括重疊使用者\(\mathcal{U}^o\)和非重疊使用者\(\mathcal{U}^x\)這兩個群體，領域\(Y\)亦然。以領域\(X\)為例，將使用者表徵\(\boldsymbol{Z}_u^X \in \mathbb{R}^{\left|\mathcal{U}^{X}\right| \times F}\)也劃分為兩個群體：\(\boldsymbol{Z}_u^{x o} \in \mathbb{R}^{\left|\mathcal{U}^o\right| \times F}\)和\(\boldsymbol{Z}_u^x \in \mathbb{R}^{\left|\mathcal{U}^x\right| \times F}\)。

資訊瓶頸正則項又可繼續分為跨域（cross-domain）資訊瓶頸正則項和領域內（in-domain）資訊瓶頸正則項。首先我們來看跨域（cross-domain）資訊瓶頸正則項，它包括包括資訊壓縮（即互資訊最小化）和重構兩部分，其結構化示意圖如下：

正如上圖（a）所示。\(\boldsymbol{Z}_u^{x o}\)，\(\boldsymbol{Z}_u^{y o}\)是編碼了各領域使用者資訊的重疊使用者表徵，而圖（b）中的\(\boldsymbol{Z}_u^x\)，\(Z_u^y\)是非重疊的（冷啟動）使用者表徵。這裡\(\boldsymbol{Z}_v^{X}\)，\(\boldsymbol{Z}_v^Y\)是物品表徵，預設是不重疊的。

以\(X\)領域遷移到\(Y\)領域為例（圖中標紅部分），我們需要使重疊使用者隱向量\(\boldsymbol{Z}^{xo}_u\)和同領域的使用者表徵\(\mathbf{X}^u\)互斥（資訊壓縮），而去接近於\(Y\)領域的互動資訊\(\mathbf{Y}\)（跨域重構）；此外，對於\(Y\)領域的物品隱向量\(\boldsymbol{Z}^Y_v\)也需要使其與物品表徵\(\mathbf{Y}^v\)互斥，並去接近於\(\mathbf{Y}\)（因為不同領域物品不會重疊，這裡採取域內重構）。

其中的跨域重構部分可以進一步通過互資訊鏈式法則化簡得到：

（這裡假設\(\boldsymbol{Z}_u^{x o}\)和\(\boldsymbol{Z}_v^Y\)獨立）

最後，\(X\)領域匯出的損失函數包括最小化（minimality）和跨域重構（reconstruction）兩部分：

接下來我們來看領域內（in-domain）資訊瓶頸正則項，其結構化示意圖如下：

我們還是以\(X\)領域為例子（圖中紅色箭頭部分），可以看到其損失函數同樣也包括最小化和領域內重構兩部分：

對比資訊正則項

在對比資訊正則化項中，作者通過最大化\(X\)的重疊使用者表徵\(\boldsymbol{Z}^{xo}_u\)和來自領域\(Y\)的重疊使用者表徵\(\boldsymbol{Z}^{yo}_u\)間的互資訊，以進一步提煉重疊使用者的表徵。對比資訊正則化項的定義如下所示：

可求解的目標函數

將上述的兩種資訊瓶頸正則項和對比資訊正則項累加起來（同時包括\(X\)和\(Y\)領域的），就得到了目標函數：

要想求解該目標函數，接下來還需要將互資訊其轉換為KL散度，比如對於\(I\left(\boldsymbol{Z}_u^{x o} ; \mathbf{X}^u\right)\)就有

該互資訊項是難以求解的，這裡需要轉而去優化其上界：

對於重構項，我們以\(I\left(\boldsymbol{Z}_u^{x o}, \boldsymbol{Z}_v^Y ; \mathbf{Y}\right)\)為例，我們有

該優化函數同樣是難解的，這裡需要轉而去優化其下界：

對於對比互資訊項，論文借鑑了infomax^[14][20]小想法，利用神經網路來度量對比互資訊。具體來說，論文定義了判別器\(\mathcal{D}\)來度量來自不同領域的重疊使用者隱向量（來自領域\(X\)的\(z^{xo}_{u_i}\)和來自領域\(Y\)的\(z^{yo}_{u_i}\)）之間的相似度。因此，對比項的下界可表示如下：

這裡

這樣，我們就將原始目標函數轉化為了最終完全可求解的目標函數。

2.2 SIGIR 2022 《DisenCDR: Learning Disentangled Representations for Cross-Domain Recommendation》^[4]

本方法屬於採用解耦表徵的跨域推薦方法。與2.1所講的基於資訊瓶頸視角的方法不同的是，本方法旨在為兩個領域中的重疊使用者做推薦，因此在模型中只考慮兩個領域中的重疊使用者。在本方法中，所要解決的關鍵問題在於對於兩個領域重疊使用者的表徵，如何分別出共用和不共用的部分？

為了解決該問題，本文基於資訊理論提出了DisenCDR模型，該模型能夠解耦領域間共用和領域特有的資訊，從而只遷移領域間共用的資訊以增強推薦表現。該方法包含了兩個互資訊正則項（包括用於解耦的正則項和用於資訊增強的正則項，詳情參見後文），並據此匯出了一個可以求解的解耦目標函數。

本文采用和上面的文章幾乎一樣的符號，就是需要注意此處領域\(X\)和領域\(Y\)的使用者空間相同。設領域\(X\)和領域\(Y\)的資料分別表示為\(\mathcal{D}^X=(\mathcal{U}, \mathcal{V}^X,\mathcal{E}^X)\)，\(\mathcal{D}^Y=(\mathcal{U}, \mathcal{V}^X,\mathcal{E}^X)\)，這裡\(\mathcal{U}\)、\(\mathcal{V}\)、\(\mathcal{E}\)分別表示每個領域使用者、物品和邊的集合。設\(\boldsymbol{A}^X=\{0,1\}^{\left|\mathcal{U}\right| \times\left|\mathcal{V}^X\right|}\)和\(A^Y=\{0,1\}^{\left|\mathcal{U}\right| \times\left|\mathcal{V}^Y\right|}\)為儲存使用者-物品互動資訊的兩個二值矩陣。

這裡\(Z^X_v\)，\(Z^X_u\)，\(Z^Y_u\)和\(Z^Y_v\)是領域特有的使用者/物品表徵，且\(Z^S_u\)是使用者的領域共用表徵，則DisenCDR的框架圖可表示如下：

注意，這裡藍色的KL意為使用先驗分佈\(\mathcal{N}(0, \mathbf{I})\)計算KL散度，綠色的KL意為計算輸入之間的KL散度。隱變數\(\widehat{Z}_u^S\)、\(\widetilde{Z}_u^S\)用於計算我們的解耦目標函數。

下面我們來詳細介紹該方法各個組成部分的細節：

嵌入層

嵌入層的作用同2.1中所述的方法相同，也即將使用者和物品嵌入到低維空間中。不過還是正如我們前面所說的，這裡\(X\)領域和\(Y\)領域的使用者空間相同。設\(\boldsymbol{U}^S\in \mathbb{R}^{|\mathcal{U}|\times F}\)為領域\(X\)和領域\(Y\)的共用初始嵌入矩陣，\(\boldsymbol{U}^X \in \mathbb{R}^{|\mathcal{U}|\times F}\)和\(\boldsymbol{V}^X \in \mathbb{R}^{\left|\mathcal{U}\right| \times F}\)分別為領域\(X\)和\(Y\)特有的初始化嵌入矩陣。此外，\(\boldsymbol{V}^X \in \mathbb{R}^{\left|\mathcal{V}^X\right| \times F}\)和\(\boldsymbol{V}^Y \in \mathbb{R}^{\left|\mathcal{V}^Y\right| \times F}\)分別為領域\(X\)和領域\(Y\)的物品表徵。

變分二分圖編碼器

DisenCDR和變分二分圖編碼器和我們 2.1 中講的第一個基於資訊瓶頸思想的模型一樣，唯一的區別就是這裡的共用隱向量同時利用了\(X\)領域的\(\boldsymbol{\overline{\mu}}_{u}^X\)和\(Y\)領域的\(\overline{\boldsymbol{\mu}}_u^Y\)：

生成和推斷

論文遵循VAE^[18]的框架，這裡假定所觀測的互動資訊\(\mathcal{D}^X\)和\(\mathcal{ D}^Y\)採自一個聯合概率分佈\(p_{\mathcal{D}}(u, v^X, v^Y)\)，每個元組\(\left(u_i, v_j, v_k\right) \sim p_{\mathcal{D}}\left(u, v^X, v^Y\right)\)描述了使用者\(u_i\)和物品\(v_j \in \mathcal{V}^X\)和物品\(v_k \in \mathcal{V}^Y\)的互動資訊。而互動資料正是經由領域共用表徵(比如\(Z_u^S\)）和領域特有（比如\(Z^X_u\)，\(Z^X_v\)，\(Z^Y_u\)和\(Z^Y_v\)）表徵生成，也即：

下圖（a）正是描述了互動資料的生成過程，而圖（b）則描述了反向推斷步驟：

在推斷過程中，直接最大化聯合概率分佈\(p_\theta\left(u, v^X, v^Y\right)\)的似然是難解的，因為後驗分佈\(p_\theta\left(Z_u^X, Z_u^Y, Z_u^S, Z_v^X, Z_v^Y \mid \mathbf{X}, \mathrm{Y}\right)\)未知。因此採用近似推斷^[19]來近似真實的後驗分佈。根據上圖（b）中的結構化假設，論文將近似後驗分佈分解為：

解耦目標函數

接下來作者從資訊理論的角度來探究領域間表徵糾纏的問題，並推導了一個解耦目標函數。

為了使領域間共用和領域特有的隱向量能夠編碼互斥的資訊，作者引入了互斥正則項來最小化二者的互資訊。為了分析最小化互資訊的影響，作者又將互資訊進行了進一步改寫。我們以領域\(X\)為例，其對應的領域共用和領域特有隱向量的互資訊\(I(Z^X_u; Z^S_u)\)可做如下改寫：

接下來我們看另外一個用於資訊增強的正則項（對應我們在2.2資訊瓶頸方法中所介紹的重構正則項）。該正則項旨在使每個領域共用的表徵\(Z^S_u\)資訊更豐富，這裡作者最大化互資訊\(I\left(Z_u^S ; \mathrm{X} ; \mathrm{Y}\right)\)來使得\(Z^S_u\)編碼領域共用的資訊。我們以領域\(X\)為例，有：

總目標函數
將上面所說的兩個解耦目標函數（包括\(X\)領域和\(Y\)領域的）加起來，就得到了總的目標函數：

進一步將物品隱向量\(Z_v^X\)和\(Z_v^Y\)引入，可以將損失函數放縮為：

這樣，解耦目標函數中的一部分可以視為變分推斷中標準的證據下界（Evidence Lower Bound， ELBO）。最後，論文按照VAE的思路，繼續將其化為了可以求解的目標函數：

參考

• [1] Lin X, Wu J, Zhou C, et al. Task-adaptive neural process for user cold-start recommendation[C]//Proceedings of the Web Conference 2021. 2021: 1306-1316.

• [2] Zhu F, Wang Y, Chen C, et al. Cross-domain recommendation: challenges, progress, and prospects[J]. arXiv preprint arXiv:2103.01696, 2021.

• [3] Hu G, Zhang Y, Yang Q. Conet: Collaborative cross networks for cross-domain recommendation[C]//Proceedings of the 27th ACM international conference on information and knowledge management. 2018: 667-676

• [4] Li P, Tuzhilin A. Ddtcdr: Deep dual transfer cross domain recommendation[C]//Proceedings of the 13th International Conference on Web Search and Data Mining. 2020: 331-339.

• [5] Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.

• [6] Meng Liu, Jianjun Li, Guohui Li, and Peng Pan. 2020. Cross Domain Recom- mendation via Bi-directional Transfer Graph Collaborative Filtering Networks. In ACM International Conference on Information and Knowledge Management (CIKM).

• [7] Xiangnan He, Kuan Deng, Xiang Wang, Yan Li, Yongdong Zhang, and Meng Wang. 2020. Lightgcn: Simplifying and Powering Graph Convolution Network for Recommendation. In ACM International Conference on Research on Development in Information Retrieval (SIGIR).

• [8] Cao J, Sheng J, Cong X, et al. Cross-domain recommendation to cold-start users via variational information bottleneck[C]//2022 IEEE 38th International Conference on Data Engineering (ICDE). IEEE, 2022: 2209-2223.

• [9] Zang T, Zhu Y, Liu H, et al. A survey on cross-domain recommendation: taxonomies, methods, and future directions[J]. ACM Transactions on Information Systems, 2022, 41(2): 1-39.

• [10] Cao J, Lin X, Cong X, et al. DisenCDR: Learning Disentangled Representations for Cross-Domain Recommendation[C]//Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval. 2022: 267-277.

• [11] Tishby N, Pereira F C, Bialek W. The information bottleneck method[J]. arXiv preprint physics/0004057, 2000.

• [12] Tishby N, Zaslavsky N. Deep learning and the information bottleneck principle[C]//2015 ieee information theory workshop (itw). IEEE, 2015: 1-5.

• [13] Alemi A A, Fischer I, Dillon J V, et al. Deep variational information bottleneck[J]. arXiv preprint arXiv:1612.00410, 2016.

• [14] M. I. Belghazi, A. Baratin, S. Rajeshwar, S. Ozair, Y. Bengio, A. Courville, and D. Hjelm, 「Mutual infor- mation neural estimation,」 in International Conference on Machine Learning (ICML), 2018.

• [15] Wu, H. Ren, P. Li, and J. Leskovec, 「Graph infor- mation bottleneck,」 in Annual Conference on Neural Information Processing Systems (NeurIPS), 2020.

• [16] S. Gershman and N. Goodman, 「Amortized inference in probabilistic reasoning,」 in Proceedings of the Annual Meeting of The Cognitive Science Society, 2014.

• [17] Wang Z, Chen X, Wen R, et al. Information theoretic counterfactual learning from missing-not-at-random feedback[J]. Advances in Neural Information Processing Systems, 2020, 33: 1854-1864.

• [18] Kingma D P, Welling M. Auto-encoding variational bayes[J]. arXiv preprint arXiv:1312.6114, 2013.

• [19] Gershman S, Goodman N. Amortized inference in probabilistic reasoning[C]//Proceedings of the annual meeting of the cognitive science society. 2014, 36(36).

• [20] Hjelm R D, Fedorov A, Lavoie-Marchildon S, et al. Learning deep representations by mutual information estimation and maximization[J]. arXiv preprint arXiv:1808.06670, 2018.