我的語言模型應該有多大？

本文發表於 2020 年 6 月 8 日，雖然時間較久遠，但現在看起來仍然是非常有價值的一篇文章。

在這個全民 LLM 的狂歡裡，想測測你拿到的預算夠訓一個多大的模型嗎？本文會給你一個答案，至少給你一個計算公式。

在自然語言處理領域，有時候我們恍惚覺得大家是為了搏頭條而在模型尺寸上不斷進行軍備競賽。 1750 億引數 無疑是一個很抓眼球數位！為什麼不考慮高效地去訓一個小一點的模型？其實，這是因為深度學習領域有一個挺驚人的縮放效應，那就是: 大神經網路計算效率更高。這是以 OpenAI 為代表的團隊在像 神經語言模型的縮放定律 這樣的論文中探索出的結論。 本文的研究也基於這一現象，我們將其與 GPU 速度估計相結合，用於確保在進行語言模型實驗時，我們能根據我們算力預算來設計最合適的模型尺寸 (劇透一下，這個大小比你想象的要大！)。我們將展示我們的方法是如何影響一個標準的語言建模基準的架構決策的: 我們在沒有任何超參優化的前提下，僅使用了原論文 75% 的訓練時間，復現了 Zhang 等人的 Transformer-XL 論文 中的 14 層模型的最佳結果。我們還估計 來自同一篇論文的 18 層模型其實僅需要比原論文少一個數量級的步數就能達到相同的結果。繼續閱讀之前想先玩玩我們的演示嗎？只需單擊 此處！

1. 停止訓練的最佳時間 (比你想象的要早)

我們先觀察一些損失曲線 (loss curve)。我們使用的任務是在 Wikitext-103 上訓練 Transformer-XL 語言模型，Wikitext-103 是一個標準的中等體量的測試基準。 GPT-2 在此等體量的資料集上表現不佳。隨著訓練的進行，我們來觀察計算成本 (通過浮點運算數來衡量) 與模型效能 (通過驗證集上的損失來衡量) 的聯動關係。我們做點實驗吧！在下圖中，不同顏色的線段表示不同層數和大小的 Transformer-XL 模型執行 200000 步的資料，這些模型除了層數與大小外的所有其他超引數都相同。模型引數量範圍從幾千到一億 (不含嵌入)。越大的模型在圖中越靠右，因為它們每一步需要的計算量更大。本圖是互動式的，你可以玩一玩！

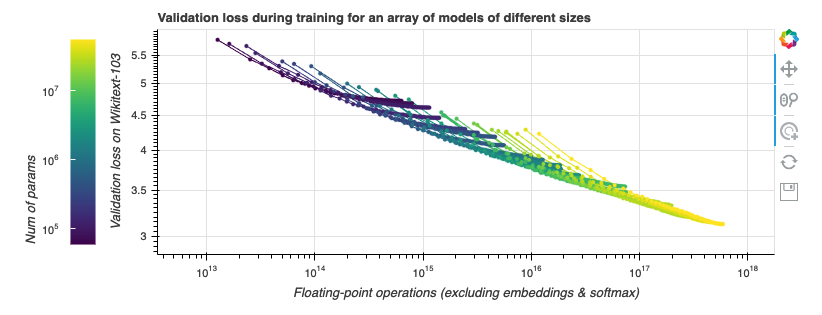
與 縮放定律 一文中的做法一樣，我們的橫軸為非嵌入浮點運算數 (non-embedding FLoating Point Operations, neFLOs)，縱軸為驗證集損失。對於給定的 neFLOs 預算，似乎存在一個任何模型都沒法越過的效能邊界，我們在圖中用紅色線段表示。在 縮放定律 一文中，它被稱為計算邊界 (compute frontier)。我們可以看到，在所有的實驗中，幾乎每個實驗都能在經過初始若干步的損失迅速降低後達到或接近該計算邊界，隨後又在訓練接近尾聲時，因訓練效率降低而偏離該計算邊界。這個現象有其實際意義: 給定固定的浮點運算預算，為了達到最佳效能，你應該選擇一個模型尺寸，使得在浮點運算預算見頂時正好達到計算邊界，然後我們就可以在此時停止訓練。此時離模型收斂所需的時間還很遠，模型收斂還需要 10 倍左右的時間。事實上，如果此時你還有額外的錢可用於計算，你應該把大部分用到增大模型上，而只將一小部分用於增加訓練步數。[ 譯者注: 這是因為效能邊界本質上度量了每 neFLOs 帶來的 loss 的降低是多少，到達計算邊界後，後面的每 neFLOs 能帶來的 loss 的降低變小，不划算了。我們應該轉而去尋求增大模型所帶來的接近計算邊界的高回報，而不應該卷在增加訓練步數帶來的低迴報上。 ]

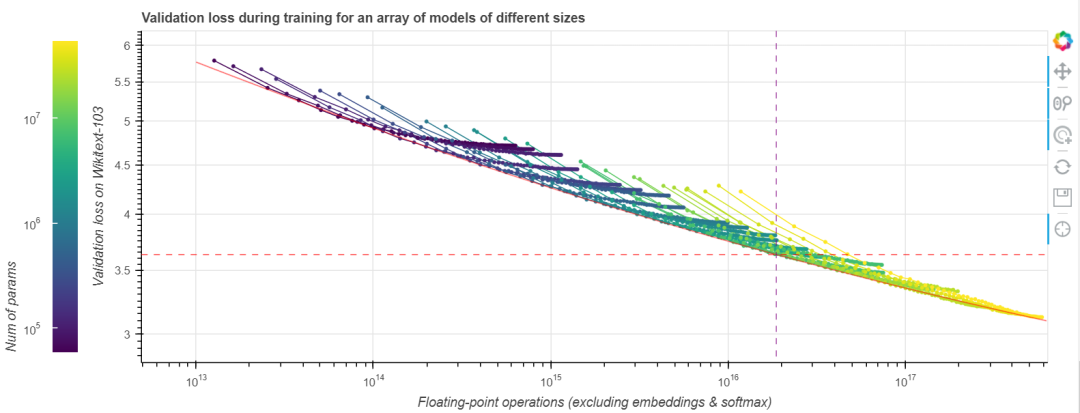
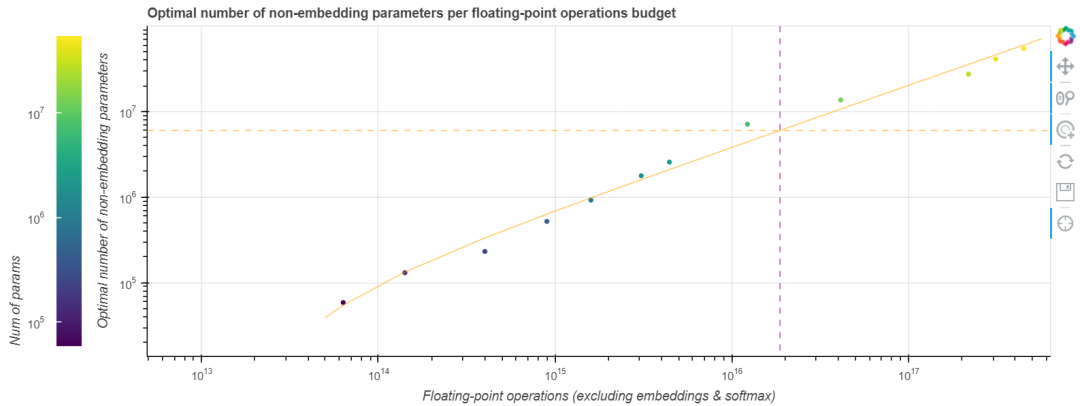
在 縮放定律 一文中，OpenAI 團隊用冪律函數擬合了一個 GPT-2 訓練的計算邊界。這似乎也適用於我們的任務，我們也擬合了一個以預算為自變數，最適合該預算的模型引數量為因變數的冪律函數。如下圖所示。

由於好的模型的 neFLOs- 損失曲線往往會與計算邊界相切比較長時間，因此最終的擬合函數會存在一些噪聲。然而，這恰恰也意味著基於該擬合函數的估計的容忍度會比較好，即使我們預測尺寸有點偏差，其結果仍然會非常接近最優值。我們發現，如果將算力預算乘以 10，最佳模型尺寸會隨之乘以 7.41，而最佳訓練步數僅乘以 1.35。將此規則外推到 Tranformer-XL 論文中的那個更大的 18 層最先進模型，我們發現 其最佳訓練步數約為 25 萬步。即使這個數位由於模型尺寸的變化而變得不那麼精確，它也比論文中所述的 收斂所需的 400 萬步 小得多。以更大的模型、更少的訓練步數為起點，在給定的 (龐大的) 預算下我們能訓到更小的損失。

2. GPU 針對大而寬的模型進行了優化

我們現在有了一個將效能和最佳模型尺寸與 neFLOs 聯絡起來的規則。然而，neFLOs 有點難以具象化。我們能否將其轉化為更直觀的指標，如訓練時間？其實，無論你是有時間上的限制還是財務上的限制，主要關注的都是 GPU 時間。為了在 neFLOs 和 GPU 時間之間建立聯絡，我們在谷歌雲平臺上用 4 種不同 GPU 範例以及各種不同大小的 Transformer-XL 模型進行了數萬次的基準測試 (包括混合精度訓練測試)。以下是我們的發現:

速度估計

每秒 neFLOs (即公式中的 speed) 可以建模為由模型寬度 (每層神經元數) 、深度 (層數) 和 batch size 三個因子組成的多變數函數，這三個因子的重要性遞減。在我們的實驗中，觀察到的最大預測誤差為測量值的 15%。

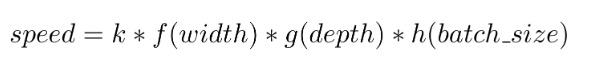
寬度

GPU 針對寬 transfomer 模型的大型前饋層進行了優化。在我們所有的實驗中，每秒 neFLOs 與模型寬度 呈 1.6 次方的冪律關係，這意味著兩倍寬的模型需要 4 倍的操作。然而執行這些操作的速度也提高了大約 3.16 倍， 幾乎抵消了額外的計算成本。

深度

每秒 neFLOs 也與深度正相關。我們目前發現的最佳關係是每秒 neFLOs 與 成正比。這與 transformer 模型必須序列地處理每一層的事實是一致的。從本質上講， 層數更多的模型其實並不會更快，但它們似乎表現出更快，其原因主要是它們的均攤開銷更小。公式中的 常數 就代表這一開銷，在我們的實驗中該常數一直在 5 左右，這其實意味著 GPU 載入資料、嵌入和 softmax 這些操作的耗時大約相當於 5 個 transfomer 層的時間。

Batch size

Batch size 發揮的作用最小。 Batch size 較小時，其與速度呈正相關關係，但這個關係很快就飽和了(甚至在 V100 和 P100 上 batch size 大於 64 後、在 K80 和 P4 batch size 大於 16 後，速度比小 batch size 時還有所降低)。因此，我們將其對速度的貢獻建模為對數函數以簡化計算，它是 3 個因子中最弱的。因此，最終我們所有實驗都是在單 GPU 上用 batch size 64 執行出來的。這是大模型的另一個好處: 因為更大的 batch size 似乎沒有多大幫助，如果你的模型太大而無法塞進 GPU，你可以只使用較小的 batch size 以及梯度累積技術。

2 的冪在 2020 年仍然很重要！

最後，一個令人驚訝的收穫是 寬度或 batch size 設定為 2 的冪的話其最終效能會比設為其他值高。有或沒有 Tensor Core 的 GPU 都是如此。在像 V100 這樣的 Tensor Core GPU 上，NVIDIA 建議張量形狀設定為 8 的倍數; 然而，我們試驗過將其不斷加倍至 512 的倍數，效能還會繼續提高。但是，在最終擬合時我們還是隻選擇擬合 2 的冪的資料，因為擬合所有資料點意味著擬合質量會變差，而且最終的擬合結果會對採用 2 的冪情況下的速度估計得過於樂觀。但這不妨礙你去選擇最快的形狀引數。

最終，我們得到執行速度的估算公式如下:

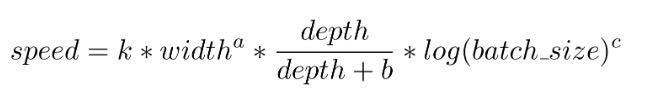
例如，在未使用混合精度的 V100 GPU 上，k=2.21 × 10^7、a=1.66、b=5.92、c=1.33。不同的 GPU 具有不同的乘性係數，但結果很接近。

3. 語言建模任務演示: Wikitext-103

現在我們已經知道了模型尺寸和訓練速度之間的關係，我們可以依此預測: 對於給定的 GPU 時間或預算，適合目標任務的最佳模型尺寸及其能達到的效能。

這裡使用的價格是 Google 雲平臺 (Google Cloud Platform，GCP) 的價格。我們使用了 Peter Henderson 的 Experiment impact tracker 來估算能源消耗，並使用了 Electricity map 的荷蘭資料 (Google 的歐洲伺服器所在地) 來估算 CO2 排放量。儘管巨大的訓練成本常常博得頭條，但事實上，我們仍然有可能以 30 美元的價格在中等規模的資料集上覆現最先進的結果！對於一個恰當優化過的訓練方案而言，V100 已經算一個強大的武器了。

圖中所示的資料的測例為在 Wikitext-103 上使用 batch size 60 以及單 GPU 訓練一個 Transformer-XL 模型，模型的目標長度 (target length) 和記憶長度 (memory length) 為 150，測試基於 CMU 的 Transformer-XL 程式碼庫。為了充分利用 V100 的 Tensor Core 功能，我們在該 GPU 上把 batch size 設為 64，序列長度設為 152。在我們的 模型尺寸 - 速度預測公式中，我們假設內部前饋層維度與嵌入和注意力維度相同，並且寬深比是恆定的。 Reformer 表明，這種設定有利於節省記憶體。雖然 縮放定律 一文表明: 形狀不會顯著影響 GPT-2 的效能。然而，對於大模型而言，我們還是發現具有更大前饋層的更淺的模型的效能會更好，因此我們在圖中給出了兩種候選的模型形狀: 一個寬而淺，一個窄而深。

為了復現中型 Transformer-XL 預訓練模型 (損失為 3.15) 的結果，我們調整了原模型的大小以增加的前饋維度並使之為 2 的高次冪，同時保持相同引數量。我們最終得到了一個 14 層的模型，隱藏層維度為 768 且前饋層維度為 1024。相比之下，原文中的模型是通過激進的超引數搜尋搜得的 16 層模型，形狀也很奇怪，隱藏層維度為 410 且前饋層維度為 2100。我們的實驗表明，由於我們的形狀是 2 的高次方，並且是一個更淺、更寬的模型，因此它在 NVIDIA RTX Titan 上每 batch 的速度比原模型提高了 20%。對於該模型，CMU 團隊提供的指令碼已經非常接近最佳停止時間。最終，我們獲得了相同的效能，同時減少了 25% 的訓練時間。最重要的是，原模型使用超引數搜尋得到了對它而言更優形狀，而我們什麼也沒調，甚至連隨機種子也是直接複用的他們手調的隨機種子。由於我們使用了較小規模的訓練來擬合縮放定律，並依此縮放定律計算所需的模型超參，因此節省引數搜尋實際上可能是我們獲得的另一個也是更大的一個收益。

4. 要點

• 大模型效率驚人！
• 訓練至收斂一點也不高效。
• 執行小規模基準測試能夠幫助我們預測生產級模型的模型效能和最佳停止時間。
• 優化模型形狀以提高速度以及使用尺寸大、停止早的模型可幫助降低訓練成本。

英文原文: https://hf.co/calculator/

原文作者: Teven Le Scao

譯者: Matrix Yao (姚偉峰)，英特爾深度學習工程師，工作方向為 transformer-family 模型在各模態資料上的應用及大規模模型的訓練推理。

審校、排版: zhongdongy (阿東)