從網際網路傳輸媒體資訊在現代已經非常普遍。因此，確保資訊傳輸的安全性非常重要。在現代網路通訊中，常用的資訊保安技術包括資料加密[1]、數位簽章[2]、可信路由策略[3]等。其中，資訊加密是保護資訊最基本的技術手段。因此，對加密演演算法的研究顯得尤為重要。影象是各種場合廣泛使用的資訊媒體。

　　但是，影象加密不能以與文字加密完全相同的方式進行。在影象加密中，需要考慮影象的一些固有特性[4]，如資料量大、資料冗餘度高、相鄰畫素之間的相關性高等。由於混沌系統具有對初始條件和控制引數極其敏感、遍歷性和類隨機行為等良好特性，混沌已成為影象加密的理想工具。因此，基於混沌的影象加密演演算法成為近年來一個頗具吸引力的研究領域，許多影象加密演演算法被提出[5]-[12]。

　　在不同的加密方案中，採用了多種策略和不同的混沌系統。 Wu 等人 [13] 利用三維 (3D) 混沌貓圖設計了一種高速對稱影象加密方案。

　　Wang 等人 [14] 提出了一種使用 3D 混沌貝克圖的快速影象加密方案。 Chai [15] 通過使用新的一維 (1D) 混沌對映構建影象加密演演算法，並模擬粒子的布朗運動來混淆普通影象的位平面。 Huang [16] 利用混沌切比雪夫發生器設計了一種影象加密演演算法。 Wang 等人 [17] 提出了一種使用交織邏輯對映和 PWLCM 對映的影象加密方案。 Ye [18] 提出了一種基於交織邏輯圖的高效對稱影象加密演演算法。 Zhu [19] 提出了一種基於改進超混沌序列的新型影象加密方案，僅通過兩輪擴散運算即可實現高金鑰靈敏度和高明文靈敏度。 Liu 和 Wang [20] 提出了一種彩色影象加密方案，其中使用分段線性混沌對映（PWLCM）和切比雪夫對映來生成金鑰流序列。 PWLCM的系統引數由切比雪夫對映生成的擾動序列修改，PWLCM的初始條件由熵的滑鼠位置的MD5雜湊值生成。

　　然而，MD5 並不安全，已被教授破解。

　　清華大學王小云。文獻[21]提出了一種利用空間位級置換和高維混沌系統的彩色影象加密方案，能夠取得良好的加密效果，並能抵抗普通攻擊。

　　但是位級排列和高維混沌系統會增加演演算法的時間開銷。文獻[22]提出了一種利用DNA互補規則和混沌對映的影象加密方案。將DNA編碼原理引入影象加密是一種新穎的方法，但DNA編碼也會增加演演算法的時間開銷。在[23]中，提出了一種具有感知器模型的混沌影象加密系統，其中使用神經網路中的高維洛倫茲混沌系統和感知器模型來增強密碼系統的安全性。

　　文獻[24]提出了一種基於旋轉矩陣位級置換和塊擴散的影象加密方案，該方案具有適合並行模式和抗噪聲攻擊的魯棒性。文獻[25]提出了一種利用離散Chirikov標準對映和基於混沌的分數階隨機變換的雙重光學影象加密方案，可以實現對光學影象的完全加密。但是分數隨機變換增加了計算的複雜度。

　　在[26]中，C.Li等人提出了一種基於混沌帳篷圖（CTM）的彩色影象加密方案，該方案只涉及擴散階段，省略了混淆階段。因此，純基於CTM的方案存在一些安全缺陷。最近，Wu 等人[27]提出了一種基於矩形變換和 CTM 的彩色影象加密方案，這是一種增強的基於 CTM 的彩色影象加密方案。 Wu 的方案包括混淆和擴散兩個階段，分別由改進的 2D Arnold 變換和混沌帳篷圖控制。這些關於加密方案設計的著作屬於密碼學的研究範疇，密碼學是密碼學的一個分支。

　　與密碼學相比，密碼分析是解密金鑰或明文的科學[28]-[30]，是密碼學的另一個分支。最近的一些研究表明，一些基於混沌的影象加密演演算法存在安全漏洞。 Li等人[28]針對葉氏方案[18]開發了純密文攻擊、已知明文攻擊和選擇明文攻擊。 Li 等人 [29] 對 Zhu 的方案 [19] 進行了已知明文攻擊。

　　Wang 等人 [30] 利用選擇明文攻擊破解了 Huang 的演演算法 [16]。對於其他一些例子，在[31]中提到了幾種被破解的基於混沌的影象加密方案。密碼分析不僅可以揭示加密演演算法的弱點，還可以幫助設計者提高加密演演算法的安全性。如果不找出加密演演算法中的安全漏洞，那麼，將不安全的演演算法應用到安全通訊中，將給通訊雙方帶來嚴重的安全隱患和損失。因此，密碼分析工作對於推動密碼學的進步具有重要意義。

　　作為典型的彩色影象加密演演算法，吳氏加密演演算法[27]具有結構簡單、加密速度快、密碼效能好的優點。

　　因此，與傳統的影象加密演演算法相比，它在處理大量資料和減少冗餘資訊方面具有優勢。但吳氏的加密方案也存在一些缺陷。

　　本文對文獻[27]提出的加密演演算法的安全性進行了重新評估，發現存在以下安全問題：（1）不能抵抗選擇明文攻擊； (2) 加密演演算法對所有亂碼也是不敏感的； (3)解密過程中無法解密密文影象中的第一個畫素點； (4) 對矩形逆變換系統的引數選擇有額外的限制。針對該安全性缺陷，提出了一種改進的彩色影象加密演演算法。

　　本文的其餘部分安排如下。第二節簡要介紹了吳氏演演算法。詳細的密碼分析和對 Wu 演演算法的攻擊在第三節中介紹。

　　第四節提出了一種改進的加密方案。

　　第五節給出了改進方案的一些實驗結果和分析。最後，第六節給出了結論。

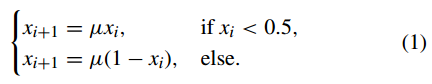
 　　Wu 演演算法中用於置換畫素位置的 2D 矩形變換是改進的 2D Arnold 變換，定義為

 　　其中 (a, b, c, d) 是變換矩陣的元素，(x, y) 和 (x 0 , y 0 ) 分別是原始影象中畫素的位置及其在置換影象中的新位置，而 m 和 n 分別是普通影象的高度和寬度。當滿足以下條件時，二維矩形變換具有逆運算，即，

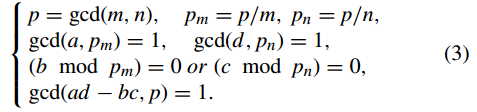
　　 則對式(2)的逆變換表示為

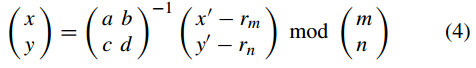
 　　Wu 演演算法的金鑰是混沌帳篷圖的 (µ1, µ2, µ3, x10, x20, x30) 和改進的 2D-RT 的 (a, b, c, d, rm, rn, t)。其中(µ1, µ2, µ3)和(x10, x20, x30)分別為CTM系統的控制引數和初始值，t為排列的迭代輪數。

B. WU 的演演算法

　　為了更清楚地描述吳氏演演算法，畫出該演演算法的流程圖，如圖1所示。

　　加密過程包括兩個階段，即排列畫素位置和加密畫素值。在密碼分析中，加密方案就像一個加密機器。圖 1 中的虛線矩形框相當於吳氏演演算法的加密機制。

　　為了更清楚地描述吳氏演演算法，畫出該演演算法的流程圖，如圖1所示。

　　加密過程包括兩個階段，即排列畫素位置和加密畫素值。在密碼分析中，加密方案就像一個加密機器。圖 1 中的虛線矩形框相當於吳氏演演算法的加密機制。

　　具體步驟可簡述如下：

　　步驟（1）：選擇祕鑰（a、b、c、d、rm、rn、t）和（μ1、μ2、μ3、x10、x20、x30）。

　　步驟(2)：讀取m×n×3大小的彩色明文影象Pm×n×3=[P(i,j,k)]。令 N = m × n，將 Pm×n×3 的三個分量表示為 RPm×n = [RP(i, j)]、GPm×n = [GP(i, j)] 和 BPm×n = [ BP(i, j)]，分別。其中 i = 1, 2, . . . , m, j = 1, 2, . . . , n, k = 1, 2, 3。

　　步驟(3)：將RPm×n、GPm×n和BPm×n三個分量拼接在一起，形成灰度影象PSm×3n = [PS(i, l)]，其中i = 1, 2, . . . , m, l = 1, 2, . . . , 3 名詞

　　步驟(4)：將灰度圖PSm×3n = [PS(x, y)]利用式(2)進行t輪置換，得到置換後的影象為PRTm×n = [PRT(x 0 , y 0 )]。其中，PRT(x 0 , y 0 ) = PS(x, y)。

　　步驟(5)：將PRTm×3n拆分為三個矩陣RRTm×n、GRTm×n和BRTm×n，大小為m×n。然後將RRTm×n、GRTm×n、BRTm×n進一步轉化為三個一維向量RN×1、GN×1、BN×1。其中 N = m × n。

　　步驟（6）：分別以引數（μ1，x10）、（μ2，x20）和（μ3，x30）對式（1）進行N+1000次迭代，取最後的N個值，形成三個混沌序列X1，長度為 N 的 X2、X3。

　　步驟（7）：用 X1，X2，X3 計算三個金鑰流 S1，S2，S3

 　　步驟（8）：對RN×1、GN×1、BN×1進行加密，得到它們對應的密文影象R 0 = [R 0 (i)], G0 = [G 0 (i)], B 0 = [ B 0 (i)] 作為

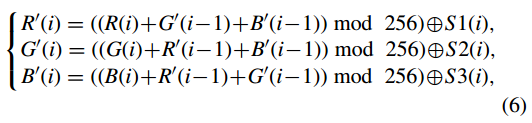
 　　其中 i = 1, 2, . . . ,N.當 i = 1 時，R 0 (i − 1)、G 0 (i − 1) 和 B 0 (i−1) 分別由三個引數 R 0 0 、G 0 0 和 B 0 代替，計算如下：

　　步驟(9)：將三個一維向量R 0 、G0 、B 0 整形為三個矩陣RCm×n、GCm×n、BCm×n，並用這三個分量組成最終的彩色密碼影象C。

　　解密演演算法是加密演演算法的逆運算。這裡將解密演演算法的兩個關鍵操作步驟簡述如下。

　　首先，在反向擴散過程中，從 R 0 、G0 和 B 0 中回收 R、G 和 B 的公式為

　　其中 i = 1, 2, . . . ,N.當i = 1時，R 0 (i − 1)、G 0 (i − 1)和B 0 (i − 1)分別被三個引數R 0 0 、G 0 0 和B 0 0 代替。值得注意的是，R(1)、G(1)和B(1)的第一個畫素值無法被解密，因為R 0 0 、G 0 0 和B 0 0 的值是未知的。這些值需要通過普通影象的畫素值來計算。

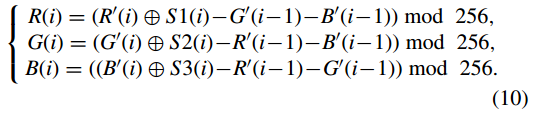
 　　其次，在反向混淆過程中，從置換灰度影象PRTm×3n恢復未置換灰度影象PSm×3n的公式為式(4)。結果，必須滿足由公式(3)表示的條件。

C. 原演演算法的主要缺陷

　　吳氏演演算法存在四個主要缺陷，歸納如下：

　　（1）吳氏演演算法使用的金鑰與要加密的明文影象無關，因此吳氏演演算法不能抵抗選擇明文攻擊。

　　(2) 當任何一個引數(µ1, µ2, µ3, x10, x20, x30)發生變化時，它只會改變其中一個序列(S1, S2, S3)。結果，Wu 的演演算法對所有金鑰都不敏感。

　　(3) 解密過程中，R 0 0 、G 0 0 、B 0 0 未知，無法計算。結果，無法解密第一個畫素。

　　(4) 在反向混淆過程中，Wu 等人。阿爾。採用逆二維阿諾德變換，要求引數（a，b，c，d）滿足式（3）表示的限制條件。

　　根據 Kerchoff 原理 [32]，在分析加密演演算法時，假設密碼分析者確切地知道密碼系統的設計和工作，除了金鑰。即攻擊者知道密碼系統的所有工作機制，但不知道金鑰。經典的攻擊型別有四種：

　　 (1) 僅密文攻擊：對手只擁有目標密文。

　　(2) 已知明文攻擊：對手擁有一串明文，以及對應的密文。

　　(3) 選擇明文攻擊：對手獲得了對加密機制的臨時存取權。因此，他或她可以選擇任何明文，並獲得相應的密文。

　　(4) 選擇密文攻擊：對手獲得了對解密機器的臨時存取權。因此，他或她可以選擇任何密文，並獲得相應的明文。

　　選擇一個全零元素組成的明文影象U，通過加密機制得到其對應的密文影象V。 U的置換影象對應的一維向量是R、G和B。V對應的一維向量是R 0 、G0和B 0 。由於置換過程沒有改變明文影象的畫素值，因此R、G、B中的畫素值都為零。

　　相應地，R 0 0 、G 0 0 和B 0 0 的值可以由式（7）得到，R 0 0 = 0，G 0 0 = 0，B 0 0 = 0。根據式（6） , 然後可以恢復金鑰流 S1, S2 和 S3 為

　　其中 i = 1, 2, . . . ,N, 在 i = 1 的情況下，R 0 (0) = R 0 0 = 0，G 0 (0) = G 0 0 = 0，B 0 (0) = B 0 0 = 0。

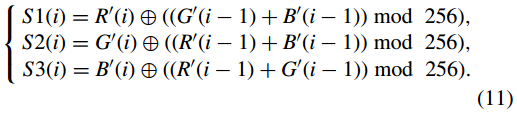
 B. 恢復位置遍歷矩陣

　　一幅大小為 m×n×3 的彩色影象有（3mn）個畫素點，每個畫素點的值是 1 到 255 之間的整數。

　　如果(3mn)≤255，則只需要一張選擇明文影象來恢復位置遍歷矩陣T，使得選擇明文影象中的每個畫素在集合{1, 2, . . . , 255}。如果(3mn)>255，則恢復位置遍歷矩陣T所需的選擇明文影象的數量為d3mn/255e，因此任意選擇的影象有255個畫素點，取值範圍為1~255，其餘畫素點有同值零。

 　　其中PS為U對應的m×3n灰度影象，I = 1, 2, . . . , d3mn/255e。利用第I個選擇的明文影象及其對應的密文影象以及前面得到的金鑰流S1、S2和S3，我們可以恢復出第I個置換影象PRT。然後我們可以通過比較第 I 個選擇的明文影象矩陣 PS 和它對應的置換灰度影象矩陣 PRT 來恢復矩陣 T 中最多 255 個元素的值。使用d3mn/255e選擇明文影象及其對應的密文影象，可以解決T中的所有（3mn）個元素。

　　在 A 子節中，我們得到了混沌金鑰流 S1、S2 和 S3，它們只與金鑰（µ1、µ2、µ3、x10、x20、x30）相關，與明文影象無關。

　　在子Section B中，我們還得到了整個置換矩陣T，它只與祕鑰(a, b, c, d, rm, rn, t)有關。因此，我們可以破解由具有相同引數（μ1、μ2、μ3、x10、x20、x30；a、b、c、d、rm、rn、t）的相同加密機制加密的任何其他密文影象 C。

　　從 C 中恢復 P 的解密過程如下：

　　步驟(1)：將彩色密碼影象C整形為一維向量R 0 、G0和B 0 的三個分量。

　　步驟(2)：對於 i = 1, 2, . . . ,N,利用式(10)恢復一維向量R、G、B中除R(1)、G(1)、B(1)之外的三個分量。由於R 0 0 、G 0 0 和B 0 0 的值未知，因此R(1)、G(1)和B(1)無法恢復。為簡單起見，我們設 R(1) = R 0 (1)、G(1) = G 0 (1)、B(1) = B 0 (1)。

　　步驟(3)：將大小為(m×n)×1的一維向量R、G、B的三個分量合併為大小為m×3n的灰度影象矩陣PRT。

　　步驟(4)：對PRT中的每個畫素位置(x,y)，利用T進行逆置換運算得到PS如下：

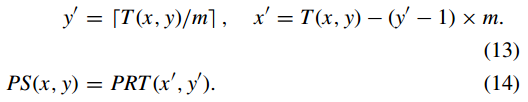
　　步驟(5)：將m×3n大小的矩陣PSm×3n拆分為三個m×n大小的矩陣，即RPm×n、GPm×n、BPm×n。

　　步驟(6)：將RPm×n、GPm×n和BPm×n三個分量組合起來，得到最終的解密彩色影象P。

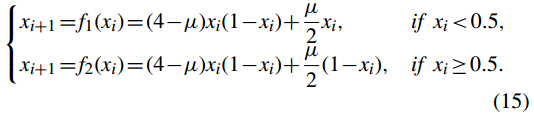
　　命題 1：如果 µ ∈ (0, 4) 且 xi ∈ (0, 1)，則系統 (15) 是一個對映 f：xi ∈(0, 1)→ xi+1 ∈ (0, 1)。

　　證明函數 f1(x) 可以轉換為標準二次函數形式：f1(x) = (µ − 4)x 2 + (4 − µ/2)x。

　　對於 µ < 4，(µ−4) < 0，因此，函數 f1(x) 在 xm = (4 − µ/2)/(8 − 2µ) = 1/2 + µ/(16 − 4µ) > 1/2。因此，當 x < 0.5 < xm 時，函數 f1(x) 單調遞增。即，f1(x < 0.5) < f1(x = 0.5) = (2 − µ/4) − (4 − µ)/4 = 1，f1(x > 0) > f1(x = 0) = 0。

　　為了比較新系統和帳篷地圖系統的混沌特性，分別使用分岔圖和李亞普諾夫指數圖描述了兩個系統的混沌動力學行為。無花果。圖3(a)和3(b)分別是帳篷圖的分岔圖和李雅普諾夫指數圖。

無花果。圖3(c)和3(d)分別是LTM的分岔圖和Lyapunov指數圖。從圖 3 可以看出，當 µ 在 (1, 2] 範圍內時，帳篷圖具有正李雅普諾夫指數，處於混沌狀態，且範圍很小。此外，混沌序列的狀態值分佈{xi} 在 [0, 1] 範圍內很不均勻。

然而，新的LTM系統具有正的Lyapunov指數，當μ在(0, 4)範圍內時處於混沌狀態，μ值的範圍遠大於帳篷圖。此外，所提出的新 LTM 系統的狀態值 {xi} 的分佈在 [0, 1] 範圍內更加均勻。

　　如果所有的 P 值 > α，則該序列被認為是隨機的。我們使用 LTM 生成三個序列並將它們轉換為三個長度為 1000000 的二進位制序列，使用 NISTSP800-22 套件測試了 15 個指標，這些序列的最小 P 值列在表 1 中。從表 1 中，我們可以看到最小P值結果大於顯著性水平α，說明檢驗滿足SP800-22隨機性要求。

　　因此，LTM 系統產生的亂數適合加密。

步驟 (1)：選擇金鑰 {a, b, c, d, rm, rn, t, µ1, µ2, µ3, x10, x20, x30}。

步驟(2)：讀取m×n×3大小的彩色明文影象Pm×n×3 = [P(i, j, k)] (i = 1, 2, . . . , m, j = 1, 2 , . . . , n, k = 1, 2, 3)，將3D矩陣Pm×n×3轉化為2D矩陣得到灰度圖PSm×3n = [PS(i, l)]，其中i = 1, 2, . . . , m, l = 1, 2, . . . , 3 × n。操作方法同吳氏加密演演算法的步驟（2）和（3）。

步驟(3)：使用SHA-3雜湊演演算法生成一個256bit的明文影象雜湊值H，可分為32個8bit大小相同的塊。即，H = h1h2。 . . h32, hi ∈ [0, 255], i = 1, 2, . . . , 32. 利用雜湊值H計算引數δ為

δ也被用作金鑰。

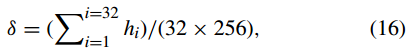
 步驟（4）：修改初始值（x10，x20，x30）為 因此，更新後的引數（x10，x20，x30）與明文影象Pm×n×3的內容有關。

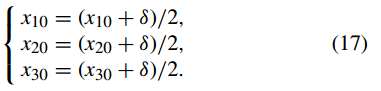
步驟(5)：對灰度影象PSm×3n進行置換，得到置換後的影象PRTm×3n。具體操作方法如下： 對PSm×3n中任意一個畫素點的位置(x,y)，將式(2)迭代t次，得到該畫素點在PRTm中的位置(x 0 ,y 0 ) ×3n。因此，我們得到 PRT(x 0 , y 0 ) 作為 PRT(x 0 , y 0 ) = PS(x, y)。對所有位置的畫素點進行處理後，得到置換影象PRTm×3n。

然後將PRTm×3n拆分為三個矩陣RRTm×n、GRTm×n、BRTm×n，大小為m×n。進一步，將 RRTm×n、GRTm×n 和 BRTm×n 轉換為三個一維向量 RN×1、GN×1 和 BN×1，大小為 N × 1。其中 N = m × n。

步驟(6)：計算三個引數R 0 0 、G 0 0 和B 0 0 為

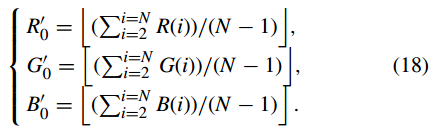
步驟(7)：分別以引數{μ1，μ2，μ3}和修正值{x10，x20，x30}迭代新混沌系統方程(15)N+1000次，取最終的N個值形成三個長度為 N 的混沌序列 X1、X2、X3。

步驟(8)：通過式(5)計算三個金鑰流S1、S2、S3和X1、X2、X3。

步驟(9)：將金鑰流S1、S2、S3修改為

 步驟(10)：對每個畫素加密三個分量{R(i), G(i), B(i)}，得到它們對應的密碼值{R 0 (i), G 0 (i), B 0 ( i)} as 當i = 1時，R 0 (i − 1)、G 0 (i − 1)和B 0 (i − 1)分別被三個引數R 0 0 、G 0 0 和B 0 0 代替，這是由等式計算的。 (18).通過使用等式。 (20)，我們使密文和明文的關係更加複雜。

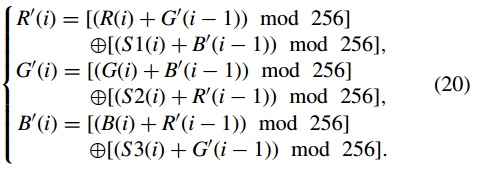
 步驟(11)：重構三個一維向量 R 0 N×1 = [R 0 (i)]，G0 N×1 = [G 0 (i)]，B 0 N×1 = [B 0 (i)]到三個矩陣RCm×n，GCm×n，BCm×n，用這三個分量組成最終的彩色密碼影象Cm×n×3。

解密過程與加密過程類似，只是運算順序相反。

步驟（1）：接收祕鑰，即引數集{a, b, c, d, rm, rn, t, µ1, µ2, µ3, x10, x20, x30, δ}。

步驟(2)：接收彩色密碼影象Cm×n×3，將三維矩陣Cm×n×3分解為三個二維分量矩陣，分別記為RCm×n、GCm×n、BCm×n。

步驟（3）：利用方程（17）用δ修改初始引數{x10，x20，x30}。

步驟（4）：分別用修改後的初始值{x10，x20，x30}和系統引數{μ1，μ2，μ3}迭代新的混沌系統方程（15）N+1000次，取最終的N個值形成三個長度為N的混沌序列X1，X2，X3。

步驟(5)：利用式(5)分別用X1、X2、X3計算三個金鑰流S1、S2、S3，並分別利用式(19)修改S1、S2、S3。

步驟(6)：將三個二維矩陣RCm×n、GCm×n、BCm×n分別整形為三個一維向量R 0 mn×1 、G 0 mn×1 、B 0 mn×1 。

步驟(7)：將R 0 mn×1 , G 0 mn×1 , B 0 mn×1 反向擴散得到部分三個解密向量Rmn×1, Gmn×1, Bmn×1 為

其中 i = N,N − 1, . . . , 2.

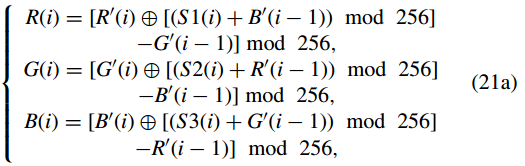
 步驟 (8)：因為現在 {R(2), R(3), . . . , R(N)}, {G(2), G(3), . . . , G(N)}, 和 {B(2), B(3), . . . , B(N)} 是已知的，因此，我們可以利用式（18）計算出（R 0 0 , G 0 0 , B 0 0 ）的值。

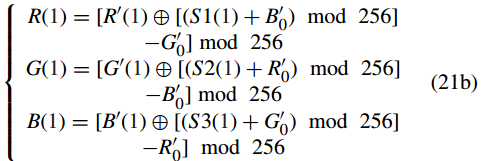
步驟(10)：將Rmn×1、Gmn×1、Bmn×1整形為三個矩陣RRTm×n、GRTm×n、BRTm×n，然後拼接成灰度影象PRTm×3n。

步驟(11)：對灰度影象PRTm×3n進行逆置換得到未置換灰度影象PSm×3n。與Wu的方法不同，這裡我們仍然使用改進的2D Arnold變換方程（2）代替逆變換方程（4）。具體操作方法如下： 對PSm×3n中任意一個畫素位置(x,y)，將式(2)迭代t次，得到該畫素在PRTm×中的位置(x 0 ,y0 ) 3n.因此，我們得到 PS(x, y) 作為 PS(x, y) = PRT(x 0 , y 0 )。對所有位置的畫素點進行處理後，得到未經置換的灰度影象PSm×3n。

步驟(12)：將PSm×3n拆分為三個矩陣，即RPm×n、GPm×n、BPm×n。

步驟(13)：最後，解密後的彩色影象Pm×n×3可以由其三個分量RPm×n、GPm×n、BPm×n組成。

D. 改進方案的理論分析

根據處理原理，改進後的方案可以克服吳氏方案的以下不足。

1）新的組合混沌系統，Logistic-tent map（LTM），混沌效能優於tent map。

2) 通過引入與明文影象的SHA-3雜湊值相關的引數作為金鑰，將金鑰流與待加密影象相關聯，使改進演演算法能夠抵抗選擇明文攻擊。

3)通過改進引數R 0 0 、G 0 0 、B 0 0 的生成方法，解密端可以準確計算出這些引數，從而實現對影象的完整解密。

4) 通過改進生成金鑰流S1、S2、S3的方法，使改進後的演演算法對(µ1、µ2、µ3、x10、x20、x30)中的每個初始金鑰更加敏感。

5) 通過改進擴散過程中的加密公式，使密文與明文的關係更加複雜。

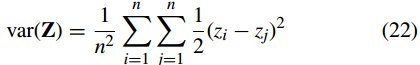
 　　在模擬實驗中，我們通過等式計算了 Lena 純影象（大小為 512×512）及其加密影象的直方圖的方差。 (22).三種不同加密演演算法加密後的Lena明文影象及其對應的密文影象的直方圖方差如表2所示。從結果可以看出，我們的演演算法得到的密文影象Lena的方差最小，即 3485.1953，遠小於 Zhang 的演演算法 [33] 和 Zhu 的演演算法 [34]。因此，我們改進的彩色影象加密演演算法更加高效和安全。

　　夏農熵 [35] 通常用於衡量影象灰度值的隨機性。對於 8 點陣影象，夏農熵定義為 其中 mi 表示第 i 個灰度值，而 P(mi) 是值 mi 存在於影象中的概率。顯然，對於一個8位元完全隨機的影象，P(mi) = 1/256，熵為8。一個好的加密演演算法應該使密文影象的夏農熵非常接近8。

　　對於大小為 m×n×3 的彩色影象，我們將其轉換為大小為 m×3n 的灰度影象來計算夏農熵。

 　　不同相關演演算法加密的不同密文影象的結果如表4所示。注意，我們的改進演演算法在大多數情況下獲得最高的熵，這意味著我們的改進演演算法在三個演演算法中洩漏的資訊最少。

 其中m、n分別表示影象中畫素的總行數和列數。 C1(i, j)和C2(i, j)是上述兩張加密影象在相同位置(i, j)的畫素值，D(i, j)計算為

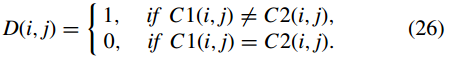
NPCR的理想值接近1，UACI的理想值接近0.3346[38]。 NPCR 和 UACI 的值越大，說明演演算法抗差分攻擊的效能越好。

　　在我們的改進方案中，金鑰流（S1、S2、S3）與要加密的明文影象相關。即使攻擊者用一些特殊選擇的明文影象破解了金鑰流（S1，S2，S3），金鑰流（S1，S2，S3）也不能用於解密目標密文影象，因為不同的影象具有不同的金鑰-流（S1、S2、S3）。

　　進一步地，在擴散過程中，加密值不僅與對應的明文值和金鑰有關，還與原明文值和原加密值有關。這意味著不同的加密影象具有不同的原明文值和原加密值。因此，改進後的演演算法可以抵抗選擇的明文/密文攻擊，並且可以很好地抵抗四種經典型別的攻擊。

　　本文分析了一種彩色影象加密演演算法，並利用選擇明文攻擊對其進行了破解。此外，我們還提出了一種改進的彩色影象加密演演算法。改進後的演演算法包括以下三個主要改進。

　　首先，提出了一種新的組合混沌系統，稱為Logistic-tent map (LTM)，它具有比tent map更好的混沌效能。

　　其次，將新的混沌系統應用到改進的加密方案中。

　　第三，通過改進金鑰生成方法和加密策略，新的加密方案可以克服原加密方案的安全缺陷。分析和實驗結果表明，改進後的演演算法能夠顯著提高加密影象的安全性，同時仍然具有吳氏演演算法的所有優點，具有更好的應用潛力。本文提出的改進影象加密演演算法適用於對安全性要求較高的彩色影象的加密，也適用於灰度影象的加密。