積體電路模擬器（SPICE）的實現原理

　　本文系統地介紹類SPICE積體電路模擬器的實現原理，包括改進節點分析（MNA）、非線性器件建模、DC/AC分析、時域/（復）頻域模擬以及涉及的數值方法。
　　基於本文原理，實現了SPICE-like模擬器：https://github.com/cassuto/CSIM

1 理論基礎

　　任何集總引數電路都能依據基爾霍夫電流定律（KCL）、基爾霍夫電壓定律（KVL）和支路約束方程建立模型並通過解析法或數值法求解，進而實現計算機輔助電路分析（CACA，Computer Aided Circuit Analysis）。

　　CACA核心：

　　1. 建立電路數學模型：

• a）拓撲約束：利用圖論分析電路，建立KCL、KVL方程。常見方法包括割集電壓法、節點分析（NA, Nodal Analysis）法和C.W. Ho\(^{[1]}\)提出的改進節點分析（MNA, Modified Nodal Analysis）法等。UC Berkeley開發的SPICE即採用MNA方法\(^{[7]}\)。
• b）元件約束：根據元件的物理特性和分析的目標建立VCR約束。（復）頻域分析可使用s域模型或相量（正弦穩態）模型建立VCR約束；時域分析則可用微分代數方程（DAE）建立VCR約束，或先使用s域模型求解最後進行Laplace逆變換。

　　2. 求解數學模型。主要有解析法和數值法兩種。並非所有模型都容易找到解析解。常採用數值方法，對於線性方程組，可用LU分解法等；對於非線性方程，需通過迭代法將其線性化。對於微分方程，常使用數值積分。

　　3. 分析模型。主要進行誤差和靈敏度分析。

　　CACA把上述過程總結為一套演演算法，讓計算機自動完成。

2 術語約定

在不同參考資料中，相關術語的定義各有差別。本文統一採用如下規定：

• 網路（Network）：描述電路拓撲的無向圖（帶參考方向時為有向圖），用\(G(V,E)\)表示；
• 網表（Netlist）：網路的一個範例；
• 端子（Pin）：元件的接線處；
• 埠（Port）：一對端子構成一個埠；
• 節點（Node）：連線兩個或兩個以上端子的交匯點；
• 支路（Branch）：對於一個二端元件，若兩個端子分別接在節點\(s\)和\(t\)上，則該二端元件構成一條支路\((s,t) \in E\)；
• 關聯（Associative）：給定節點\(n\)，如果存在支路\((s,t) \in E\)滿足\(s=n\)或\(t=n\)，就稱該支路與節點\(n\)關聯；
• 迴路（Circuit）：如果從節點\(n_0\)出發，能沿與之關聯的支路\(b_0\)到達節點\(n_1\)，再以\(n_1\)為起點，重複上述過程並最終返回節點\(n_0\)，並且形成的存取序列\(<n_0,b_0,n_1,b_1,\cdots ,n_0>\)沒有重複的節點，則該序列指出一個迴路；

3 改進節點分析（MNA）前置內容

　　MNA是節點分析（NA）的增廣，這裡先介紹NA，如果您對此熟悉可以跳過本節。

3.1 NA方程的推導

　　我們從拓撲學角度推導NA方程。

　　將電路抽象為網路。首先為網路中各支路指定電流參考方向，使其成為有向網路，設其關聯矩陣為：\(\mit{A}_{n \times b} = \begin{bmatrix} a_{jk} \end{bmatrix} = \begin{cases} 1, & \text{支路k參考電流從節點j流出}\\ -1, & \text{支路k參考電流從節點j流入} \\ 0, & \text{支路k與節點j無關聯} \end{cases}\)

　　其中\(n\)為節點個數，\(b\)為支路個數。

　　設支路電壓向量為\(\mit{U}=\begin{bmatrix} u_1, u_2, \cdots ,u_b \end{bmatrix} ^\mathrm{T}\)；支路電流向量為\(\mit{I}=\begin{bmatrix} i_1, i_2, \cdots ,i_b \end{bmatrix} ^\mathrm{T}\)。

　　根據KCL定律\(^{[2]}\)：

　　其中\(\mit{I}_s=\begin{bmatrix} i_{s_1}, i_{s_2}, \cdots ,i_{s_n} \end{bmatrix} ^\mathrm{T}\)為注入電流，\(i_{s_j}>0\)表示電流注入節點\(j\)，反之表示電流流出節點\(j\)。

　　設節點電壓向量為\(\mit{U}_n=\begin{bmatrix} u_{n_1}, u_{n_2}, \cdots ,u_{n_n} \end{bmatrix} ^\mathrm{T}\)。在網路中任意選定一個節點作為參考節點，對於餘下\((n-1)\)個節點，規定節點電壓為該節點相對於參考節點的電位差。

　　根據KVL定律\(^{[2]}\)：

　　設支路導納矩陣為：

　　通過導納描述支路約束方程：

　　將式\((\ref{NA_KVL})\)代入式\((\ref{NA_BRAN})\)，得到：

　　再將式\((\ref{NA_KVL_BRAN})\)代入式\((\ref{NA_KCL})\)中，得到：

　　令\(\mit{Y} = \mit{A}\mit{G}\mit{A}^\mathrm{T}\)，最終得到節點分析方程：

　　其中\(\mit{Y}\)稱為節點導納矩陣。

　　給定網表可計算節點導納矩陣\(\mit{Y}\)，也可由電流源支路確定\(\mit{I}_s\)（若無，置0）。最後只需解上述線性代數方程組，即可得出節點電壓\(\mit{U_n}\)。

3.2 節點導納矩陣的物理意義

　　上節已經推出節點導納矩陣的表示式：

　　按照關聯矩陣的定義，若支路\(k\)與節點\(i\)或\(j\)無關聯，則\(a_{ik}a_{jk}=0\)。若支路\(k\)與節點\(i\)與\(j\)均有關聯，則\(a_{ik}=\pm 1\)且\(a_{jk}=\mp 1\)，此時有\(a_{ik}a_{jk}=\begin{cases} -1 & (i \ne j) \\ 1 & (i = j) \end{cases}\)。

　　由此可知，\(\sum\limits_{k=1}^{b} g_k \cdot (a_{ik}a_{jk}) =y_{ij} \space (i \ne j)\)的物理意義為：若節點\(i\)與節點\(j\)之間有直接關聯的支路（\(i \ne j\)），則\(y_{ij}\)就是兩節點\(i\)和\(j\)之間關聯的所有支路的導納之和取負數，否則\(y_{ij}=0\)。把它定義為互導\(y_{ij} \space (i \ne j)\)。
　　\(\sum\limits_{k=1}^{b} g_k \cdot (a_{ik}a_{ik})=y_{ii}\)的物理意義為：\(y_{ii}=\sum\limits_{j=1 \\ j \neq i}^{n} y_{ij}\)，即所有與節點\(i\)直接關聯的支路的導納之和，把它定義為自導\(y_{ii}\)。

　　於是節點導納矩陣就能簡單表示為：

　　下面以一個範例來說明這種表示的好處：

　　按照自導和互導的物理意義，就能直接知道節點1的自導\(y_{11}\)為\(R_3\)和\(U_1\)的電導之和，節點1到2的互導\(y_{12}\)為\(U_1\)的電導取負數，其它同理，可直接得出節點導納矩陣如下：

　　需要注意\(y_{1,3}=y_{3,1}=0\)，\(y_{2,4}=y_{4,2}=0\)，因為節點1和3、2和4之間沒有直接關聯的支路。另外，因為U1是理想電壓源，\(G_{U_1}=\infty\)，因此這個電路用NA無法直接求解，這個例子揭示了NA的侷限性。

4 改進節點分析（MNA）的原理

　　節點分析（NA）直接處理含無伴電壓源（內阻為0）的支路時會遇到困難，因為這些支路的導納為無窮大，方程無法求數值解。上文圖1中的\(U_1\)就屬於這種情況。

　　MNA解決NA侷限性的思路很簡單：對NA方程組進行增廣。NA只分析節點電壓，而MNA能同時分析支路電流，將兩種狀態變數混合在一起求解。

　　MNA混合方程如下：

　　其中\(\mit{Y}\)是節點導納矩陣；\(\mit{U}\)是節點電壓向量；\(\mit{I}\)是節點電流向量，對應方程\(\mit{Y}\mit{U}=\mit{I}\)與NA無異。此外，\(\mit{J}\)是支路電流向量，\(\mit{B}\)、\(\mit{C}\)、\(\mit{D}\)、\(\mit{E}\)是新增加的方程的係數矩陣。

　　這些係數矩陣用「橡皮圖章」法（Rubber Stamps）機械地生成\(^{[1]}\)，實現電路分析的程式化。

4.1 方程生成演演算法

　　C.W. Ho提出的元件橡皮圖章演演算法（Element Rubber Stamps）\(^{[1]}\)可以根據網表直接生成各子矩陣的值。演演算法初始時\(\mit{Y}=\mit{B}=\mit{C}=\mit{D}=\mit{I}=\mit{E}=0\)。遍歷網表中所有元件，每遇到一個元件\(e\)，就將該型別元件對應的貢獻值\(c(e)\)加到相應的子矩陣，遍歷結束時各子矩陣就有了正確的值，從而直接產生方程組。因為每種元件的貢獻值是常數，可以將貢獻值編製成表格，也稱為「表格法」。

　　在稍後的推導中可以看到，演演算法「將貢獻值加到對應子矩陣」的的理論依據是線性電路的疊加性。MNA本來只能處理線性電路，但是稍後可以看到如何利用線性化處理非線性電路。

　　方程生成演演算法可以描述為：

　　演演算法的關鍵是貢獻值\(c_Y(e)\)、\(c_B(e)\)、\(c_C(e)\)、\(c_D(e)\)、\(c_I(e)\)、\(c_E(e)\)。

　　下面推導了一些常見一埠和二埠線性元件的貢獻值。

4.2 常見一埠線性元件對Y、B、C、D、I、E的貢獻

　　假設一埠元件所在支路為\(k\)，電壓與電流取關聯參考方向\(s \rightarrow t\)。

4.2.1 阻抗元件

　　設元件導納為\(y\)，支路約束方程為：

　　其中\(i_k\)為元件所在支路電流。

　　整理上式得：

　　對應MNA矩陣形式為：

　　如果多個阻抗元件併入支路，則支路的導納就是它們之和。因此每當一個阻抗元件併入支路\(s \rightarrow t\)時，只需在MNA方程的分塊矩陣Y中加上導納：

即加上貢獻值：

4.2.2 獨立電壓源（VS）

　　設VS的電壓值設定為\(e_s\)。支路約束方程為：

　　其中\(i_k\)為VS所在支路的電流。

　　對應MNA矩陣形式為：

　　如果多個電壓源串在同一支路，則支路電壓為它們之和，因此每當一個VS串入支路\(s \rightarrow t\)時，只需加上貢獻值：

4.2.3 獨立電流源（CS）

　　設CS電流值設定為\(i_k\)，支路約束方程為：

　　如果多個電流源併入支路，則支路總電流就是它們之和，因此每當一個CS併入支路\(s \rightarrow t\)時，只需加上貢獻值：

　　上述這些例子其實反映了線性電路的疊加性。這就是為什麼任何元件加入電路時都只需在MNA對應矩陣加上貢獻值。

4.3 常見二埠線性元件對Y、B、C、D、I、E的貢獻

　　假設元件的埠1所在支路為\(k\)，電壓與電流取關聯參考方向\(s \rightarrow t\)；埠2所在支路為\(c\)，電壓與電流取關聯參考方向\(p \rightarrow q\)。

4.3.1 電壓控制電壓源（VCVS）

　　設VCVS電壓放大倍數為\(\mu\)，控制電壓為\((u_p - u_q)\)。支路約束方程為：

　　其中\(i_k\)為VCVS受控埠所在支路的電流。

　　對應MNA矩陣形式為：

　　可知每當一個VCVS加入支路\(s \rightarrow t\)、\(p \rightarrow q\)時，貢獻為：

4.3.2 電壓控制電流源（VCCS）

　 設VCCS的轉移電導為\(g\)，控制電壓為\((u_p - u_q)\)。支路約束方程為：

　　對應MNA矩陣形式為：

　　可知每當一個VCCS加入支路\(s \rightarrow t\)、\(p \rightarrow q\)時，貢獻為：

4.3.3 電流控制電壓源（CCVS）

　　設CCVS的轉移電阻為\(r\)，控制電流為\(i_c\)，支路約束方程為：

　　其中\(i_k\)為CCVS受控埠所在支路電流。

　　對應MNA矩陣形式為：

　　可知每當一個CCVS加入支路\(s \rightarrow t\)、\(p \rightarrow q\)時，貢獻為：

4.3.4 電流控制電流源（CCCS）

　　設CCCS的電流放大倍數為\(\alpha\)，控制電流為\(i_c\)。支路約束方程為：

　　對應矩陣形式為：

　　可知每當一個CCCS加入支路\(s \rightarrow t\)、\(p \rightarrow q\)時，貢獻為：

5 稀疏矩陣計算

　　對於線性電路，按照上述方法可以建立MNA方程：

　　直接採用高斯列主元素消元法、LU分解法、雅各比迭代法等都能求解上述方程，具體參考教科書[3]。

　　但是，求解稠密矩陣方程需要\(O(n^3)\)的時間。如果觀察到電路對應的係數矩陣\(\mit{A}\)是稀疏矩陣，就可以使用更優化的演演算法，因為而稀疏矩陣中存在大量零元素，利用稀疏矩陣演演算法，儲存和計算時都可以跳過大量零元素，從而使演演算法所需的時間和空間大幅減少。

6 非線性元件的分析

　　MNA可以方便地分析線性電路，但無法直接處理非線性電路。

　　幸運的是，如果利用迭代法將非線性元件線性化，使每一步迭代都能用等效的線性元件替代，就能利用MNA分析和求解非線性電路。SPICE就採用這種方法\(^{[7]}\)。

6.1 牛頓-拉夫遜法求解非線性MNA方程

　　牛頓-拉夫遜法（Newton-Ralfsnn's method）是最常用求解非線性方程近似根的演演算法。

　　牛頓-拉夫遜法通過如下迭代格式計算非線性方程\(f(\mit{x}) = \mit{0}\)的近似根\(\mit{x}\)：

　　根據MNA方程\((\ref{MNA})\)，設

　　根據式\((\ref{equ:newtown_fx})\)：

　　這其中涉及的雅克比矩陣有：

　　利用雅可比矩陣將式\((\ref{equ:newtown_fx})\)改寫為：

　　再將式\((\ref{equ:fMNA})\)代入，整理可得迭代格式：

　　即\(\mit{A}'(\mit{x}^{(k)}) \cdot \mit{x}^{(k+1)}=\mit{z}'(\mit{x}^{(k)})\)，可見迭代格式與線性代數方程組形式保持一致。給定初值\(\mit{x}^{(0)}\)，計算\(\mit{A}'(\mit{x}^{(0)})\)、\(\mit{z}'(\mit{x}^{(0)})\)，然後求解線性代數方程組，得到\(\mit{x}^{(1)}\)，再將\(\mit{x}^{(1)}\)作為新的初值，重複上述過程，生成迭代序列\(\{\mit{x}^{(k)}\}\)，直到\(\|\mit{x}^{(k+1)} - \mit{x}^{(k)}\|\)小於設定的誤差限時，可認為迭代收斂，取近似根\(\tilde{\mit{x}} = \mit{x}^{(k+1)}\)。

　　牛頓-拉夫遜迭代的本質是將非線性問題分成若干線性問題，這就啟發我們用該方法實現元件的線性化，從而允許用MNA分析非線性元件。

6.2 理想PN接面模型

　　理論上任何非線性元件都可以用動態電壓源或電流源等效代替。為了便於應用MNA，這裡使用動態電流源代替。

　　設理想PN接面位於支路\(s \rightarrow t\)上，理想PN接面電流的近似方程為：

　　其中\(I_0\)為反向飽和電流，\(U_T\)為溫度電壓當量，這兩個引數都是由物理特性決定的。

　　將PN接面作為動態電流源注入支路\(s \rightarrow t\)，根據獨立電流源支路的結論\((\ref{equ:cs_contrib})\)，有：

　　代入牛頓-拉夫遜迭格式\((\ref{equ:mna_newtown_format})\)：

　　對比之前推出的阻抗元件支路的結論（式\(\ref{equ:mna_y_comp}\)），可以認為\((\ref{equ:pn_newtown_left})\)描述的是等效電阻，其電導\({g_d}^{(k)}\)隨迭代次數\(k\)動態變化，然而在本輪迭代內是不變的，可視作線性元件：

　　再考慮式\((\ref{equ:mna_newtown_format})\)，右邊式子可展開為：

　　其中：

　　從物理意義上看，式\((\ref{equ:PN_i_d})\)描述的是動態電流源\(i_d\)與動態電阻\(g_{eq}\)並聯，如圖2所示，這樣就實現了元件的線性化，每次迭代都可以用MNA分析了。

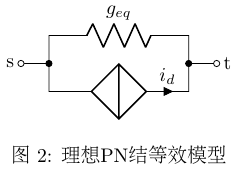
　　至此式\((\ref{equ:mna_newtown_format})\)左右兩邊都已確定，得到MNA方程組：

　　每當一個理想PN接面加入支路\(s \rightarrow t\)時，只需對子矩陣作如下更新：

　　值得注意的是整個求解過程是迭代進行的，每輪迭代都要重新計算等效電路的引數並重新求解MNA，即：

　　給定初值\(\mit{x}^{(0)}\)（這其中包含PN接面兩端的節點電壓\({u_s}^{(0)}\)、\({u_t}^{(0)}\)），代入式\((\ref{equ:pn_newtown_left})\)和式\((\ref{equ:pn_newtown_right})\)可得線性代數方程組\((\ref{equ:new_rn_mna})\)，解線性代數方程組可以得到\(\mit{x}^{(1)}\)，再將\(\mit{x}^{(1)}\)作為新的初值，如此迭代。當相鄰兩次迭代獲得的解\(\mit{x}^{(k+1)}\)與\(\mit{x}^{(k)}\)滿足\(\| \mit{x}^{(k+1)}-\mit{x}^{(k)} \| \lt \epsilon\)時，就可認為迭代收斂，可以取近似解\(\mit{x}^{(k+1)}\)。

　　下面給出了非線性電路分析的演演算法流程。

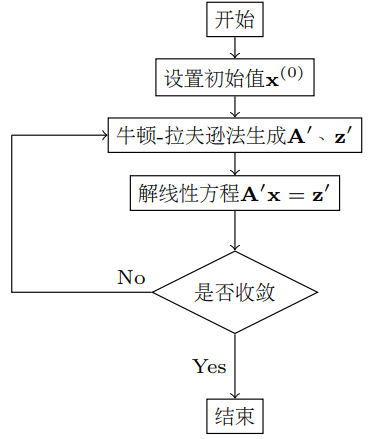
6.2.1 收斂性問題

　　在PN接面特性方程的牛頓-拉夫遜迭代中，存在如下圖所示的異常情況：

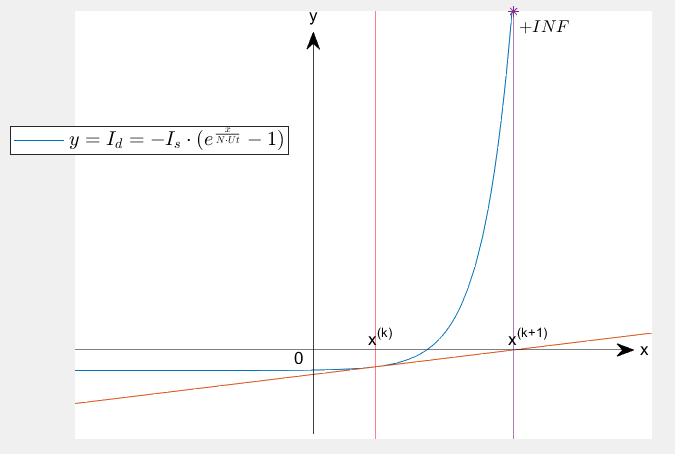
　　圖中第\(k+1\)步迭代時，由於指數函數的迅猛增長，\(i_d^{(k+1)}\)超出機器數所能表示的範圍，產生上溢，使得迭代無法進行下去。

　　考慮到實際電路中不可能出現如此大的電流（雙精度浮點數最大值約為\(10^{308}\)）；另外在結電流方程中，當\(y\)急劇增長時，\(x\)的變化範圍卻很小。因此可以將PN接面電壓限制在較小範圍內，以避免數值溢位\(^{[6]}\)。

　　PN接面臨界電壓是V-I曲線中曲率半徑最小的點，當PN接面電壓大於臨界電壓時，結電流開始急劇增加，因此可用PN接面臨界電壓\(U_{th}\)作為閾值的參考。

　　一種最簡單的閾值限制演演算法是\(x'= max(x, 10U_{th})\)，將結電壓限制在\(10U_{th}\)以下，但限制後的V-I曲線在\(U_d=10U_{th}\)處的導數不存在，大於\(10U_{th}\)後導數為0，造成不收斂。

　　SPICE中的限制演演算法\(^{[7]}\)更合理，當\(U_d > U_{th}\)時，採用以電流\(I_d\)為變數的迭代（解決反函數）；當\(U_d \le U_{th}\)時，採用正常的迭代格式。

6.3 收斂條件

　　對於MNA方程中的節點電壓\(U\)和支路電流\(J\)，SPICE採用獨立的收斂條件。設\(\xi_r\)為相對誤差限，\(\xi\)為絕對誤差限。當：

　　並且，當\(|J^{(k+1)} _b- J^{(k)}_b| \le \xi_r \cdot J_{b,max} + \xi\)時，認為迭代收斂。

　　其中\(U_{n,max}=max(|U^{(k+1)}_n|, |U^{(k)}_n|)\)；\(U^{(k+1)}_n, U^{(k)}_n\)為相鄰兩次迭代的結果。\(J_b\)同理。

7 直流掃描分析（DC Sweep）

　　至此，我們搭建的框架可以實現SPICE的第一個應用——直流掃描分析，即遍歷引數，輸出各引數下電路的靜態工作點。

7.1 特殊情形

　　直流分析反映的是輸入為直流（即頻率\(\omega=0\)）時的狀態，需要特殊處理動態元件。

　　電容在直流下的容抗為$ \lim \limits_{\omega \rightarrow 0} \frac{1}{j \omega C} = \infty $，顯然直流分析時電容應視為兩端開路。

　　電感在直流下的感抗為$ \lim \limits_{\omega \rightarrow 0} j \omega L = 0 $，顯然直流分析時應視為兩端短路。

　　此外所有作為訊號源的電壓源視為短路、作為訊號源的電流源視為開路。

7.2 直流分析的過程

　　設目標引數\(p\)，掃描範圍\([p_{min}, p_{max}]\)，掃描步長\(s\)。線性掃描共需要\(\frac{p_{max}-p_{min}}{s}\)次方程求解，每次將目標引數設定為\(p(n)=p_{min}+ns\)，通過改進節點分析（MNA）建立的方程解出對應的節點電壓\(U(n)\)。這樣\(U(n)\)就形成了直流掃描分析的結果。

　　實用中，有時需要使用對數步進來掃描。

8 交流掃描分析（AC Sweep）

　　AC Sweep分析是正弦穩態電路在頻域上的小訊號分析。輸入變數是正弦頻率\(\omega\)，輸出變數是電路中各節點電壓的頻率響應（幅度和相位）。

　　交流分析採用相量法，電壓電流都採用相量表示，仍然利用MNA求解，只不過MNA中各矩陣都定義在複數域上。

8.1 電容的相量模型

　　理想電容在正弦穩態電路中的VCR表示為

　　每當一個理想電容加入支路\(s \rightarrow t\)時，只需對MNA的子矩陣的值作如下更新：

8.2 電感的相量模型

　　類似地，理想電感在正弦穩態電路中的VCR表示為

　　每當一個電感加入支路\(s \rightarrow t\)時，只需對MNA的子矩陣的值作如下更新：

8.3 交流分析的過程

　　交流分析非常重要的假設是小訊號。在小訊號模型中，非線性元件可以在靜態工作點處線性化，例如PN接面可通過動態電阻\(g_d(u)\)等效。因此在進行交流分析之前，先進行直流分析，確定電路靜態工作點。靜態工作點確定，式\((\ref{equ:mna_newtown_format})\)中所有雅克比矩陣的值也都確定。這樣在交流分析時，不必迭代，而是將其視作線性方程來處理。

9 複頻域分析（s域）

　　對電路的微分方程進行Laplace變換可以得到s域上的代數方程，這些代數方程可以用與上一節AC分析相同的方法建立和求解。事實上，上節所述的相量模型可以看作\(s = j\omega\)的特殊情況，這也反映了頻域和複頻域的關係。

　　s域的MNA混合方程變為：

9.1 Laplace變換

　　給定時域激勵訊號f(t)，可通過Laplace變換得到複頻域上的激勵\(F(s)=\mathscr{L}[f(t)]\)，將F(s)代入激勵源模型中，求解MNA方程即可得到節點電壓和分支電流的頻域響應\(\begin{bmatrix} \mit{U(s)} & \mit{J(s)} \end{bmatrix}^{T}\)。

9.2 Laplace逆變換

　　對於上面得到的頻域響應，可通過逆變換得到時域響應\(\begin{bmatrix}\mathscr{L}^{-1}[\mit{U(s)}] & \mathscr{L}^{-1}[\mit{J(s)}]\end{bmatrix}^{T}\)。

10 瞬態分析（時域分析）

　　上節給出了從複頻域變換到時域的分析方法，下面直接在時域進行分析，這也是SPICE採用的方法。

　　時域上理想電容和電感的VCR為常微分方程：

　　計算機無法直接處理連續時間系統。可以將時間離散化，然後利用數值方法求解。

10.1 線性多步：隱式GEAR法

　　對於電容或電感特性方程中所出現的形如\(f(x,t) = \frac{dx}{dt}\)的常微分方程，可通過積分\(x = \int f(x,t) dt\)來求解。

　　根據黎曼積分的定義，連續時間域上的積分\(x = \int f(x,t) dt\)可通過離散時間域上的累積來近似：

　　其中\(h_n=t_{n+1}-t_n\)稱為第\(n\)步的步長。

　　將式\((\ref{equ:num_int})\)寫成迭代格式：

　　這是一階顯式單步法。單步法的收斂性可參考資料\(^{[3]90-92}\)。為了獲得更精確的解，這裡採用線性多步法。線性多步法是前\(p\)步解的線性組合，單步法正是線性多步法的特例。

　　其中\(p\)是步數。\(a_i\)、\(b_i\)是常係數。

　　利用泰勒展開構造線性多步法\(^{[5]}\)，\(a_i\)、\(b_i\)應滿足：

　　選取一些特殊的\(p\)、\(a_i\)、\(b_i\)值，就能構造出不同的迭代方法。當\(b_{-1} \ne 0\)時為隱式方法，當\(b_{-1} = 0\)時為顯式方法。對於隱式GEAR：

　　給定階數\(k=1,2,\cdots\)，聯立式\((\ref{equ:gear_pb})\)與式\((\ref{equ:lin_multi_step_ab})\)可以解出係數\(a_i\)、\(b_i\)。從結果來看，一階隱式GEAR就是隱式尤拉法（Implicit Euler's method）。4階隱式GEAR迭代格式如下：

10.2 線性多步法中的迭代

　　線上性多步法迭代格式\((\ref{equ:multi_step_format})\)中，式子左側為待求的量\(x_{n+1}\)，而式子右側也依賴於待求量\(x_{n+1}\)，因此待求量無法直接計算。解決辦法是解方程，設方程\(f(x_{n+1}) = x_{n+1} - \sum_{i=0}^{p}a_i x_{n-i} + h_n\sum_{i=-1}^{p}b_i f(x_{n-i},t_{n-i}) = 0\)，則只需通過迭代解出該方程的根\(x_{n+1}\)即可。迭代格式為：

　　迭代到\(\|x_{n+1}^{m+1}-x_{n+1}^{m}\|\)小於給定誤差限時，可以取\(x_{n+1}=x_{n+1}^{m+1}\)。

10.3 預報-校正法

　　從上節可以看出，每步線性迭代中又包含若干\(x_{n+1}^{m+1}=g(x_{n+1}^{m})\)這樣的迭代。初值\(x_{n+1}^0\)的選取將直接影響到迭代次數，因此初值的選取十分重要。相比於隨機給定一個初值，通過預報器預測的初值可能更接近真實值，再進行線性多步迭代時，所需迭代次數將減少。

　　這裡採用顯式尤拉法實現預報器，預報值\(x_{n+1}^{0}\)計算為

10.4 自適應步長控制演演算法

　　瞬態分析中，如果時間步長\(h_n\)選取過大會造成區域性截斷誤差偏大，甚至得出完全錯誤的結果；而如果步長選取太小則會使得計算量增加，而固定步長在某些區間內往往不是最優，因此一般採用變步長演演算法。

　　由6.3節可知，\(h_n\)的選取應使得第\(n\)步的區域性截斷誤差\(\xi_{L}^{(n+1)} = |x(t_{n+1}) - x_{n+1}|\)滿足：

　　其中\(\xi\)是設定的絕對誤差限；\(\xi_r\)是設定的相對誤差限。一般來說區域性截斷誤差無法精確計算，只能通過Milne公式估計。

　　自適應步長控制中，先設定一個足夠小的初始步長\(h_0\)，每進行一次迭代，就計算出本次迭代的區域性截斷誤差\(\xi_{L}^{(n+1)}\)，再通過式\((\ref{equ:adpt_step})\)判定步長的好壞：

• 若\(q \gt 1\)，則說明區域性截斷誤差大於設定的誤差限，步長偏大；
• 若\(q \lt 1\)，則說明區域性截斷誤差已經小於設定誤差限，若q遠小於1則說明步長過小。

　　根據\(q\)對步長進行動態調整：

　　其中\(k\)是線性多步法的階數。

　　假設當前模擬時間為\(t_{n+1}\)，首先利用線性多步法求出解\(x_{n+1}\)，再估計區域性截斷誤差\(\xi_{L}^{(n+1)}\)，按上式計算新步長\(h'_{n+1}\)，若\(h'_{n+1}<h_{n+1}\)，則說明區域性截斷誤差過大，此時模擬時間不向前推進，而是按新步長重新計算當前時間的解\(x_{n+1}\)，重複上述過程；反之則說明區域性截斷誤差已經滿足要求，模擬時間可以推進到\(t_{n+2}\)，令\(h_{n+2}=h'_{n+1}\)，結束本次步長調整。

　　下圖為瞬態模擬範例：

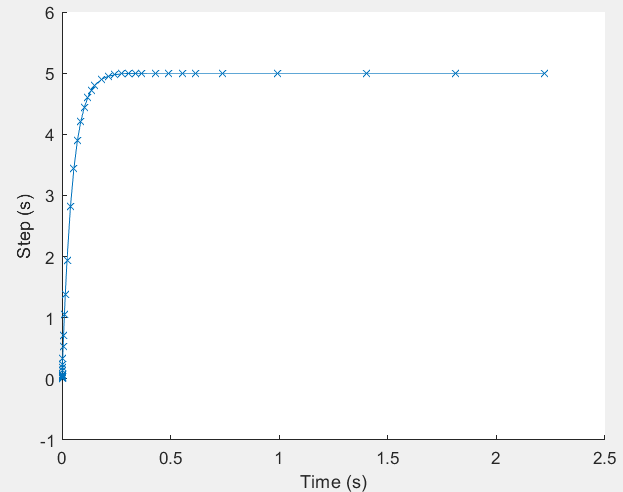
　　圖中顯示了步長自適應調整，時間軸是均勻的。

10.4.1 斷點

　　演演算法能保證每步迭代區域性截斷誤差的估計值不超出規定的誤差限，然而，每次調整步長都要重新計算線性方程組，對於訊號快速變化的電路（例如開關電路），步長可能會頻繁振盪，從而使模擬器將大量時間花費在尋找合適的步長上。

　　另一個問題出現在維持大步長時（如上圖中的平穩部分）突然發生離散事件。在混合數位模擬中，波形存在大量間斷點（電平跳變的瞬間）。步長過大會直接越過間斷點。需要注意在事件驅動的數位模擬系統中，模擬模擬的誤差估計並不會考慮離散事件造成的的跳變，這就是為什麼自適應步長控制會失敗。

　　因此，涉及數位-模擬混合模擬時，必須使用斷點（simulink中稱為過零檢測）技術，在電平跳變之前插入斷點。使模擬模擬器在時間到達斷點前，強制減少積分步長，避免錯過離散事件。對於模擬模擬，特別是涉及受控開關時，斷點同樣重要，可有效避免步長振盪。

　　稍微解釋一下為什麼數位模擬可以預測電平跳變。每個事件從進入佇列到被排程執行，需間隔該事件指定的延時，因此事件的執行總是慢於入隊。在事件入隊時，就可預知斷點的位置（入隊時間+延遲），從而提前通知SPICE模擬器。

以後有機會可能補充離散-連續系統聯合模擬的方法。

10.5 常見儲能元件的時域模型

10.5.1 電容的時域模型

　　電容的時域特性描述為：

　　利用線性多步法\((\ref{equ:multi_step_format})\)得到迭代格式：

　　將上式展開並移項（\(b_{-1} \ne 0\)），可得

　　其中：

　　\(g_{eq}\)從物理上可解釋為等效電導，\(i_{eq}\)從物理上可解釋為等效電流源，於是得到了電容的等效線性化模型，如圖4所示。

　　根據之前推出的阻抗元件支路對MNA各子矩陣的貢獻（式\(\ref{equ:admit_elem_contrib}\)）和獨立電流源支路對MNA各子矩陣貢獻值（式\(\ref{equ:cs_contrib}\)）可知對應MNA方程為：

　　因此可知每當一個電容加入支路\(s \rightarrow t\)時，只需對MNA各子矩陣作如下更新：

　　同時應在程式中應設定標記，指出引數\({g_{eq}}^{(n)}\)和\({i_{eq}}^{(n)}\)是需要迭代計算的。給定步長\(h_n\)，初值\(u_0={u_s}^{(0)}-{u_t}^{(0)}\)，根據上式生成MNA方程，可解出節點電壓\({u_s}^{(1)}\)、\({u_t}^{(1)}\)，以此類推。

10.5.2 電感的時域模型

　　電感的時域特性描述為：

　　利用線性多步法\((\ref{equ:multi_step_format})\)得到迭代格式：

　　整理並移項（\(b_{-1} \ne 0\)），可得

　　其中：

　　從物理意義上看，電感可等效為動態電阻\(r_{eq}\)與獨立電壓源\(u_{eq}\)串聯，如圖5所示。

　　根據之前推出的獨立電壓源的貢獻值（式\(\ref{equ:vs_contrib}\)）和電流控制電壓源支路對MNA各子矩陣貢獻值（式\(\ref{equ:ccvs_contrib}\)）可知對應MNA方程為：

　　因此每當一個電感加入支路\(s \rightarrow t\)時，只需對MNA各子矩陣作如下更新：

　　同時應在程式中應設定標記，指出引數\({r_{eq}}^{(n)}\)和\({u_{eq}}^{(n)}\)是需要迭代計算的。

10.6 時域分析總流程

• 1 初始化：建立MNA方程。設定當前時間\(t=0\)，設定積分步\(s\)、階數\(ord\)為初值
• 2 用\(s\)、\(ord\)計算GEAR係數
• 3 解MNA方程（流程圖見6.2）
• 4 更新時間\(t'=t+s\)
• 5 檢查斷點列表，動態調整積分步\(s\)、階數\(ord\)
• 6 判斷終止條件，不終止則迴圈執行 2

11 程式實現

　　詳見文章開頭給出的github連結。

參考資料

[1] C.W. Ho; Ruehli, A.; Brennan, P. The modified nodal approach to network analysis[J]. IEEE, doi:10.1109/tcs.1975.1084079, 1975: 0–509.

[2] 邱關源. 電路[M]. 第5版, 高等教育出版社, 2006: 391-392.

[3] 李建良等. 計算機數值方法[M]. 東南大學出版社, 2009.

[5] Timothy Sauer. Numerical Analysis[M]. 2nd Edition, George Masonry University, 2011: 336-339.

[6] Thomas L. Quarles. Analysis of performance and convergence issues for circuit simulation[R], University of California, Berkeley Technical Report No. UCB/ERL M89/42, 1989: 30-31.

[7] L. W. Nagel. SPICE2: A Computer Program to Simulate Semiconductor Circuits[R]. University of California, Berkeley Technical Report No. UCB/ERL M520, 1975: 138-142