LeetCode 周賽 335,純純手速場!
本文已收錄到 AndroidFamily,技術和職場問題,請關注公眾號 [彭旭銳] 提問。
大家好,我是小彭。
昨晚是 LeetCode 第 335 場周賽,你參加了嗎?這場周賽整體難度不高,有兩道模板題,第三題和第四題應該調換一下位置。
小彭的 Android 交流群 02 群來了,公眾號回覆 「加群」 加入我們~

2582. 遞枕頭(Easy)
題目地址
https://leetcode.cn/problems/pass-the-pillow/
題目描述
n 個人站成一排,按從 1 到 n 編號。
最初,排在隊首的第一個人拿著一個枕頭。每秒鐘,拿著枕頭的人會將枕頭傳遞給隊伍中的下一個人。一旦枕頭到達隊首或隊尾,傳遞方向就會改變,隊伍會繼續沿相反方向傳遞枕頭。
- 例如,當枕頭到達第
n個人時,TA 會將枕頭傳遞給第n - 1個人,然後傳遞給第n - 2個人,依此類推。
給你兩個正整數 n 和 time ,返回 t

題解一(模擬)
簡單模擬題。
class Solution {
fun passThePillow(n: Int, time: Int): Int {
var index = 1
var flag = true
for (count in 0 until time) {
if (flag) {
if (++index == n) flag = !flag
} else {
if (--index == 1) flag = !flag
}
}
return index
}
}
複雜度分析:
- 時間複雜度:$O(time)$
- 空間複雜度:$O(1)$
題解二(數學)
以 n = 4 為例,顯然每 n - 1 次傳遞為一輪,則有 time % (n - 1) 分辨出奇數輪 / 偶數輪。其中偶數輪是正向傳遞,奇數輪是逆向傳遞。
- 偶數輪:2 → 3 → 4,time = 1 時傳遞到 2 號;
- 奇數輪:3 → 2 → 1。
- …
class Solution {
fun passThePillow(n: Int, time: Int): Int {
val mod = n - 1
return if (time / mod % 2 == 0) {
(time % mod) + 1
} else {
n - (time % mod)
}
}
}
複雜度分析:
- 時間複雜度:$O(1)$
- 空間複雜度:$O(1)$
2583. 二元樹中的第 K 大層和(Medium)
題目地址
https://leetcode.cn/problems/kth-largest-sum-in-a-binary-tree/
題目描述
給你一棵二元樹的根節點 root 和一個正整數 k 。
樹中的 層和 是指 同一層 上節點值的總和。
返回樹中第 k 大的層和(不一定不同)。如果樹少於 k 層,則返回 -1 。
注意,如果兩個節點與根節點的距離相同,則認為它們在同一層。
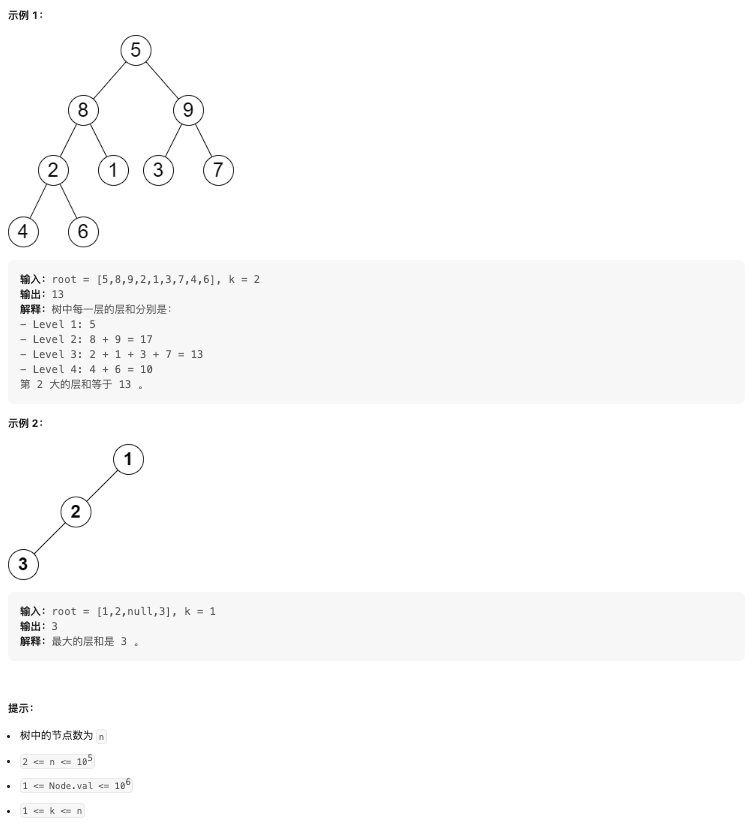
題解(BFS + 堆)
BFS 模板題,使用小頂堆記錄最大的 k 個數。
class Solution {
fun kthLargestLevelSum(root: TreeNode?, k: Int): Long {
if (null == root) return 0L
val heap = PriorityQueue<Long>()
// BFS
val queue = LinkedList<TreeNode>()
queue.offer(root)
while (!queue.isEmpty()) {
var levelSum = 0L
for (count in 0 until queue.size) {
val node = queue.poll()
levelSum += node.`val`
if (null != node.left) {
queue.offer(node.left)
}
if (null != node.right) {
queue.offer(node.right)
}
}
if (heap.size < k) {
heap.offer(levelSum)
} else if (heap.peek() < levelSum) {
heap.poll()
heap.offer(levelSum)
}
}
return if (heap.size >= k) heap.peek() else -1L
}
}
複雜度分析:
- 時間複雜度:$O(nlgk)$ 其中 $n$ 是節點數。二元樹每個節點最多入隊一次,二元樹最大有 $n$ 層,小頂堆維護 $k$ 個數的時間複雜度為 $O(nlgk)$;
- 空間複雜度:$O(n)$ 小頂堆空間 $O(k)$,遞迴棧空間最大 $O(n)$。
2584. 分割陣列使乘積互質(Medium)
題目地址
https://leetcode.cn/problems/split-the-array-to-make-coprime-products/
題目描述
給你一個長度為 n 的整數陣列 nums ,下標從 0 開始。
如果在下標 i 處 分割 陣列,其中 0 <= i <= n - 2 ,使前 i + 1 個元素的乘積和剩餘元素的乘積互質,則認為該分割 有效 。
- 例如,如果
nums = [2, 3, 3],那麼在下標i = 0處的分割有效,因為2和9互質,而在下標i = 1處的分割無效,因為6和3不互質。在下標i = 2處的分割也無效,因為i == n - 1。
返回可以有效分割陣列的最小下標 i ,如果不存在有效分割,則返回 -1 。
當且僅當 gcd(val1, val2) == 1 成立時,val1 和 val2 這兩個值才是互質的,其中 gcd(val1, val2) 表示 val1 和 val2 的最大公約數。
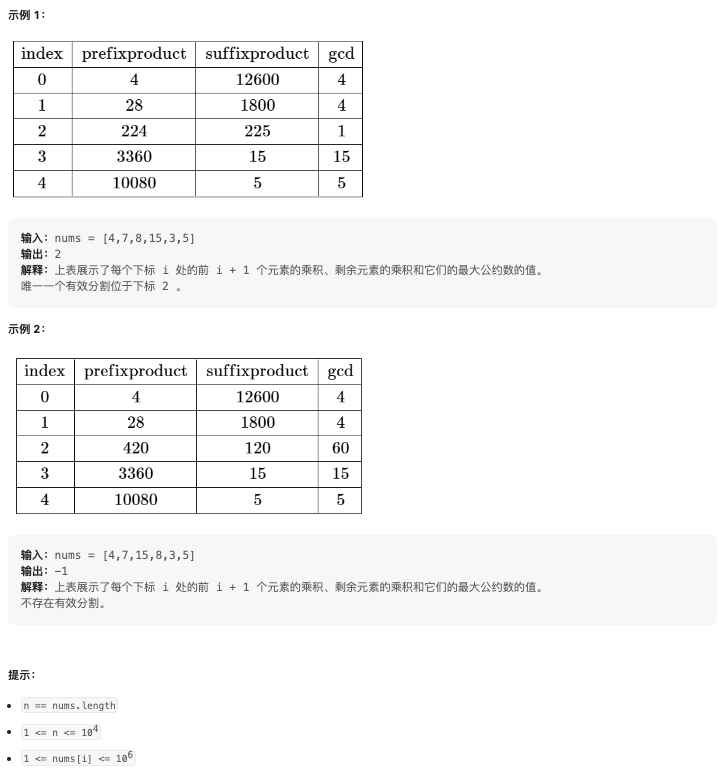
題解(質因子分解)
這道題是這場周賽中最複雜的題目,應該放在 T4。
因為多個數相乘的結果會溢位(如果題目中存在 0 還會干擾),所以這道題不能用前字尾分解的思路。 比較容易想到的思路是做質因子分解:顯然合法分割數點的左右兩邊不能有公共質因子,否則子集的乘積必然是非互質的。
舉個例子,在陣列 [1, 2, 3, 2, 5] 中,將質因子 2 劃分到不同子集的方案是錯誤的:
- [1 | 2, 3, 2, 5]:錯誤分割
- [1 , 2 | 3, 2, 5]:正確分割
- [1 , 2, 3 | 2, 5]:正確分割
- [1 , 2, 3, 2 | 5]:錯誤分割
腦海中有閃現過狀態壓縮,但題目輸入資料較大無法實現,只能有雜湊表記錄質因子資訊。因此我們的演演算法是:先對 nums 陣列中的每個元素做質因數分解,然後列舉所有分割點,統計左右子集中質因子的出現次數。如果出現同一個質因子再左右子集中的出現次數同時大於 1,說明分割點不成立。
class Solution {
fun findValidSplit(nums: IntArray): Int {
val n = nums.size
// 質因子計數
val leftCount = HashMap<Int, Int>()
val rightCount = HashMap<Int, Int>()
// 質因子分解
val primeMap = HashMap<Int, HashSet<Int>>()
for (num in nums) {
// 對 num 做質因數分解
primeMap[num] = HashSet<Int>()
var x = num
var prime = 2
while (prime * prime <= x) {
if (x % prime == 0) {
// 發現質因子
primeMap[num]!!.add(prime)
rightCount[prime] = rightCount.getOrDefault(prime, 0) + 1
// 消除所有 prime 因子
while (x % prime == 0) x /= prime
}
prime++
}
if(x > 1) {
// 剩下的質因子
primeMap[num]!!.add(x)
rightCount[x] = rightCount.getOrDefault(x, 0) + 1
}
}
// 列舉分割點
outer@ for (index in 0..n - 2) {
for (prime in primeMap[nums[index]]!!) {
leftCount[prime] = leftCount.getOrDefault(prime, 0) + 1
rightCount[prime] = rightCount[prime]!! - 1
}
for ((prime, count) in leftCount) {
if (rightCount[prime]!! != 0) continue@outer
}
return index
}
return -1
}
}
複雜度分析:
- 時間複雜度:$O(n\sqrt{U}+n·m)$ 其中 $n$ 是 $nums$ 陣列的長度,U 是陣列元素的最大值,$m$ 是 $U$ 範圍內的質數個數 $\frac{U}{logU}$ 。時間複雜度分為兩部分,質因數分解佔用 $O(n\sqrt{U})$,列舉分割點的每輪迴圈需要列舉所有質數,佔用 $O(n·m)$;
- 空間複雜度:$O(n·m + m)$ 質因子分解對映表和計數表。
題解二(質因數分解 + 合併區間)
思路來源:靈茶山艾符的題解
統計每種質因子在陣列中出現的起始位置 left 和終止位置 right,如果分割點位於 [left, right) 區間,那麼左右兩子集一定會存在公共質因子。
因此我們的演演算法是:將質數的分佈看成一個連續區間,按照區間起始位置對所有區間排序。遍歷區間並維護最大區間終止位置 preEnd,如果當前區間與 preEnd 不連續,則說明以當前位置為分割點的方案不會拆分割區間,也就找到目標答案。
如果按照這個思路理解,這道題本質上和 55. 跳躍遊戲 類似。
class Solution {
fun findValidSplit(nums: IntArray): Int {
// 質因子區間 <首次出現位置,末次出現位置>
val primeMap = HashMap<Int, IntArray>()
// 質因數分解
for ((index, num) in nums.withIndex()) {
// 對 num 做質因數分解
var x = num
var prime = 2
while (prime * prime <= x) {
if (x % prime == 0) {
// 發現質因子
primeMap.getOrPut(prime) { intArrayOf(index, index) }[1] = index
// 消除所有 prime 因子
while (x % prime == 0) x /= prime
}
prime++
}
if (x > 1) {
// 剩下的質因子
primeMap.getOrPut(x) { intArrayOf(index, index) }[1] = index
}
}
// 區間排序
val areaList = primeMap.values.toMutableList()
Collections.sort(areaList) { e1, e2 ->
e1[0] - e2[0]
}
// 列舉區間
var preEnd = 0
for (area in areaList) {
if (area[0] > preEnd) return area[0] - 1
preEnd = Math.max(preEnd, area[1])
}
return -1
}
}
複雜度分析:
- 時間複雜度:$O(n\sqrt{U}+mlgm+m)$ 質因數分解時間 $O(n\sqrt{U})$,排序時間 $O(mlgm)$,列舉區間時間 $O(m)$;
- 空間複雜度:$O(m + lgm)$ 質因子區間陣列佔用 $O(m)$,排序遞迴棧空間 $O(lgm)$。
題解三(合併區間 + 排序優化)
題解二中的排序時間可以優化。
由於我們是從前往後分解 nums 陣列,每分解一個質因子 prime 時,它一定可以更新該質數區間的末次出現位置。所以我們不用等到最後再做一次區間排序,直接在做質因數分解時維護 preEnd。在題解二中,我們是從區間的維度維護 preEnd,現在我們直接從 nums 陣列的維度維護 preEnd。
class Solution {
fun findValidSplit(nums: IntArray): Int {
val n = nums.size
// start[p] 表示質數 p 首次出現為止
val start = HashMap<Int, Int>()
// end[i] 表示以 i 為左端點的區間的最大右端點
val end = IntArray(n)
// 質因數分解
for ((index, num) in nums.withIndex()) {
// 對 num 做質因數分解
var x = num
var prime = 2
while (prime * prime <= x) {
if (x % prime == 0) {
// 發現質因子
if (!start.containsKey(prime)) {
start[prime] = index
} else {
end[start[prime]!!] = index
}
// 消除所有 prime 因子
while (x % prime == 0) x /= prime
}
prime++
}
if (x > 1) {
// 剩下的質因子
if (!start.containsKey(x)) {
start[x] = index
} else {
end[start[x]!!] = index
}
}
}
var preEnd = 0
for (index in 0 until n) {
if (index > preEnd) return index - 1
preEnd = Math.max(preEnd, end[index])
}
return -1
}
}
複雜度分析:
- 時間複雜度:$O(n\sqrt{U}+m)$ 質因數分解時間 $O(n\sqrt{U})$,列舉陣列時間 $O(n)$;
- 空間複雜度:$O(n)$ $end$ 陣列空間。
2585. 獲得分數的方法數(Hard)
題目地址
https://leetcode.cn/problems/number-of-ways-to-earn-points/
題目描述
考試中有 n 種型別的題目。給你一個整數 target 和一個下標從 0 開始的二維整數陣列 types ,其中 types[i] = [counti, marksi] 表示第 i 種型別的題目有 counti 道,每道題目對應 marksi 分。
返回你在考試中恰好得到 target 分的方法數。由於答案可能很大,結果需要對 109 +7 取餘。
注意,同型別題目無法區分。
- 比如說,如果有
3道同型別題目,那麼解答第1和第2道題目與解答第1和第3道題目或者第2和第3道題目是相同的。

題解(揹包問題)
這是分組揹包模板題,OIWiki-揹包 DP。
定義 $dp[i][j]$ 表示以物品 $[i]$ 為止且分數為 $j$ 的方案數,則有:
$dp[i][j] = dp[i - 1][j] + \sum_{k=0}^{k=j/count_i}dp[i - 1][j - k*·marks_{si}]$
class Solution {
fun waysToReachTarget(target: Int, types: Array<IntArray>): Int {
val MOD = 1000000007
// 揹包問題
val n = types.size
// dp[i][j] 表示以 [i] 為止且分數為 j 的方案數
val dp = Array(n + 1) { IntArray(target + 1) }.apply {
// 不選擇且分數為 0 的方案數為 1
this[0][0] = 1
}
// 列舉物品
for (i in 1..n) {
val count = types[i - 1][0]
val mark = types[i - 1][1]
for (j in target downTo 0) {
dp[i][j] += dp[i - 1][j]
for (k in 1..Math.min(count, j / mark)) {
dp[i][j] = (dp[i][j] + dp[i - 1][j - k * mark]) % MOD
}
}
}
return dp[n][target]
}
}
完全揹包可以取消物品維度優化空間:
class Solution {
fun waysToReachTarget(target: Int, types: Array<IntArray>): Int {
val MOD = 1000000007
// 揹包問題
val n = types.size
// dp[i][j] 表示以 [i] 為止且分數為 j 的方案數
val dp = IntArray(target + 1).apply {
// 不選擇且分數為 0 的方案數為 1
this[0] = 1
}
// 列舉物品
for (i in 1..n) {
val count = types[i - 1][0]
val mark = types[i - 1][1]
for (j in target downTo 0) {
for (k in 1..Math.min(count, j / mark)) {
dp[j] = (dp[j] + dp[j - k * mark]) % MOD
}
}
}
return dp[target]
}
}
複雜度分析:
- 時間複雜度:$O(target·C)$ 其中 $C$ 是所有 $count_i$ 之和。
- 空間複雜度:$O(target)$