LeetCode 雙週賽 99，純純送分場！

本文已收錄到 AndroidFamily，技術和職場問題，請關注公眾號 [彭旭銳] 提問。

大家好，我是小彭。

昨晚是 LeetCode 第 99 場雙週賽，你參加了嗎？這場周賽整體難度很低，第 4 題評論區普遍認為是 1 字頭，純純手速場。

小彭的 Android 交流群 02 群來了，公眾號回覆「加群」加入我們~

2578. 最小和分割

題目地址

https://leetcode.cn/problems/split-with-minimum-sum/

題目描述

給你一個正整數 num ，請你將它分割成兩個非負整數 num1 和 num2 ，滿足：

num1 和 num2 直接連起來，得到 num 各數位的一個排列。
- 換句話說，num1 和 num2 中所有數位出現的次數之和等於 num 中所有數位出現的次數。
num1 和 num2 可以包含前導 0 。

請你返回 num1 和 num2 可以得到的和的最小值。

注意：

num 保證沒有前導 0 。
num1 和 num2 中數位順序可以與 num 中數位順序不同。

題解（排序 + 貪心）

第一題相對有點思維。

思考 1：越高位的數位對結果的影響越大，所以優先排列最小的數位；
思考 2：如果劃分兩個數位的長度不均，會放大最終的值；

演演算法：對數位排序，從小到大分別排列到兩個數位上。

class Solution {
    fun splitNum(num: Int): Int {
        val array = "$num".toCharArray()
        array.sort()
        var num1 = 0
        var num2 = 0
        for (index in array.indices step 2) {
            num1 = num1 * 10 + (array[index] - '0')
            if (index + 1 < array.size) {
                num2 = num2 * 10 + (array[index + 1] - '0')
            }
        }
        return num1 + num2
    }
}

簡化寫法：

class Solution {
    fun splitNum(num: Int): Int {
        val array = "$num".toCharArray().sorted()
        var nums = Array(2) { StringBuilder() }
        for (index in array.indices) {
            nums[index % 2].append(array[index])
        }
        return "${nums[0]}".toInt() + "${nums[1]}".toInt()

複雜度分析：

時間複雜度：$O(mlgm)$ 其中 $m$ 是 $num$ 數位的位數，即 $m = lg,num$。排序時間為 $O(mlgm)$，拆分時間為 $O(m)$；
空間複雜度：$O(m)$ 字串空間為 $O(m)$，排序遞迴棧空間為 $O(lgm)$。

2579. 統計染色格子數

題目地址

https://leetcode.cn/problems/count-total-number-of-colored-cells/

題目描述

有一個無窮大的二維網格圖，一開始所有格子都未染色。給你一個正整數 n ，表示你需要執行以下步驟 n 分鐘：

第一分鐘，將任一格子染成藍色。
之後的每一分鐘，將與藍色格子相鄰的所有未染色格子染成藍色。

下圖分別是 1、2、3 分鐘後的網格圖。

題解（找規律）

找規律題。這道題可以用重力加速度類比，重力加速度的 G 是 9.8m/s，而這裡的 G 是 4格/s。

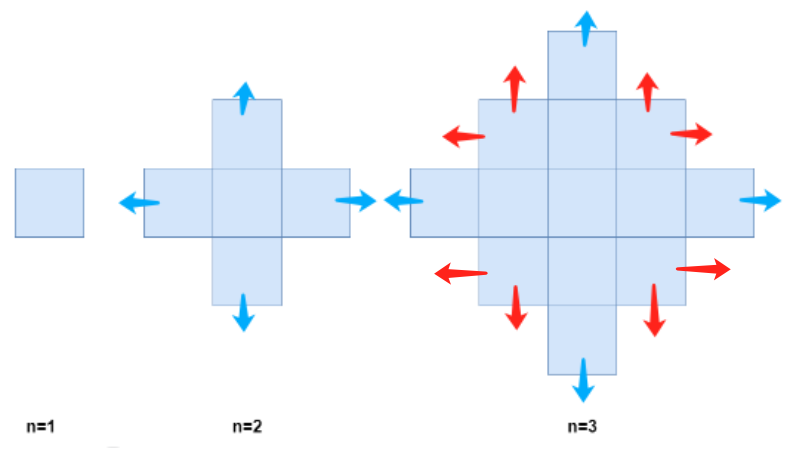
最開始只有一格，我們先放到一邊單獨計算，有 $f(1) = 1$；
從 (n = 1) 遞推到 (n = 2) 時的速度為 4，因此 $f(2) = 4 + 1 = 5$；
從 (n = 2) 遞推到 (n = 3) 時的速度為 8，因此 $f(3) = 8 + f(2) = 13$；
以此類推，從 (n - 1) 遞推到 (n) 時的速度是 $4 *(n - 1)$，即 $f(n) = f(n - 1) + 4(n - 1)$。

顯然有：

$f(n)=\begin{cases}
1, &n=1\
f(n-1) + 4(n-1) & n>1
\end{cases}$

可以看到， $n > 1$ 的分支是一個從 0 開始的等差數列，等差數列求和公式知道吧，整理得：$f(n) = 1 + 4 * n * (n - 1) / 2 = 2n^2 - 2n + 1$

class Solution {
    fun coloredCells(n: Int): Long {
        return 2 * n * n - 2 * n + 1
    }
}

複雜度分析：

時間複雜度：$O(1)$
空間複雜度：$O(1)$

2580. 統計將重疊區間合併成組的方案數

題目地址

https://leetcode.cn/problems/count-ways-to-group-overlapping-ranges/

題目描述

給你一個二維整數陣列 ranges ，其中 ranges[i] = [starti, endi] 表示 starti 到 endi 之間（包括二者）的所有整數都包含在第 i 個區間中。

你需要將 ranges 分成兩個組（可以為空），滿足：

每個區間只屬於一個組。
兩個有交集的區間必須在 同一個 組內。

如果兩個區間有至少一個公共整數，那麼這兩個區間是 有交集 的。

比方說，區間 [1, 3] 和 [2, 5] 有交集，因為 2 和 3 在兩個區間中都被包含。

請你返回將 ranges 劃分成兩個組的 總方案數 。由於答案可能很大，將它對 109 + 7 取餘後返回。

題解（排序 + 貪心）

這道題我第一時間想到了這兩道題：

後來在評論區看到更接近的原題，好嘛，怪不得印象很深。

435. 無重疊區間

腦海中有閃現過並查集，但顯然沒有必要。

演演算法：將區間看成時間段，先按照開始時間對區間排序，然後在遍歷區間的同時維護已經佔用的最晚結束時間 preEnd。如果當前區間的開始時間早於 preEnd，說明區間重合。遍歷完陣列後求出集合個數 m，求 m 個元素放到 2 個位置的方案數，顯然每個位置有 m 中可能，因此結果是 $2^m$。

class Solution {
    fun countWays(ranges: Array<IntArray>): Int {
        val MOD = 1000000007
        Arrays.sort(ranges) { e1, e2 ->
            e1[0] - e2[0]
        }
        var m = 0
        var preEnd = -1
        for (range in ranges) {
            if (range[0] > preEnd) {
                // 無交集
                m++
            }
            preEnd = Math.max(preEnd, range[1])
        }
        return pow(2, m, MOD)
    }

    private fun pow(x: Int, n: Int, mod: Int): Int {
        var ans = 1
        for (count in 0 until n) {
            ans = (ans * x) % mod
        }
        return ans
    }
}

複雜度分析：

時間複雜度：$O(nlgn + n + lgm)$ 其中 $n$ 是 $nums$ 陣列的長度，$m$ 是無交集區間的集合個數，冪運算時間為 $O(m)$；
空間複雜度：$O(lgn)$ 排序遞迴棧空間。

2581. 統計可能的樹根數目

題目地址

https://leetcode.cn/problems/count-number-of-possible-root-nodes/

題目描述

Alice 有一棵 n 個節點的樹，節點編號為 0 到 n - 1 。樹用一個長度為 n - 1 的二維整數陣列 edges 表示，其中 edges[i] = [ai, bi] ，表示樹中節點 ai 和 bi 之間有一條邊。

Alice 想要 Bob 找到這棵樹的根。她允許 Bob 對這棵樹進行若干次猜測。每一次猜測，Bob 做如下事情：

選擇兩個 不相等 的整數 u 和 v ，且樹中必須存在邊 [u, v] 。
Bob 猜測樹中 u 是 v 的 父節點 。

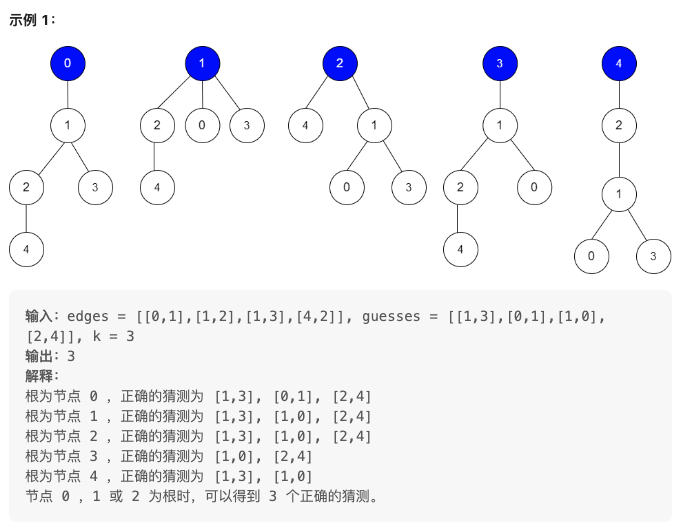
Bob 的猜測用二維整數陣列 guesses 表示，其中 guesses[j] = [uj, vj] 表示 Bob 猜 uj 是 vj 的父節點。

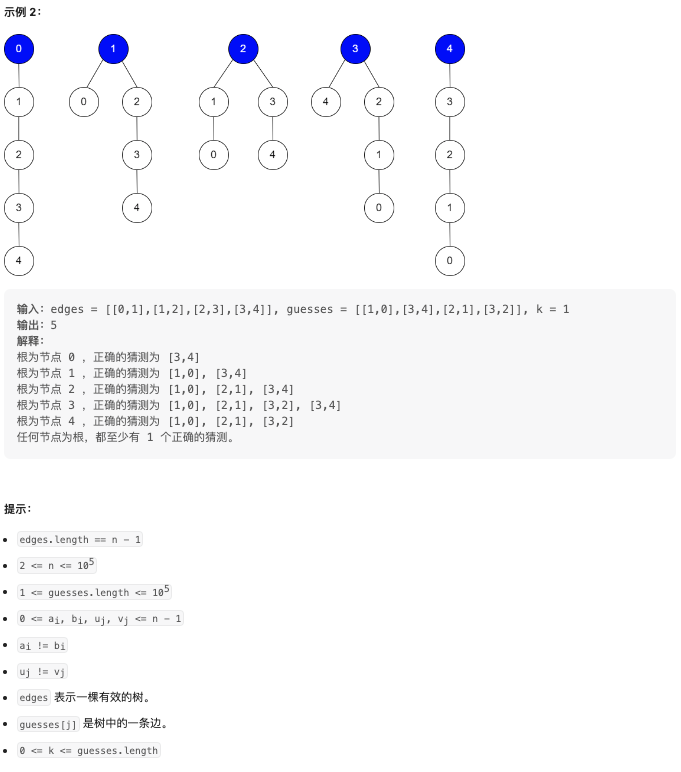
Alice 非常懶，她不想逐個回答 Bob 的猜測，只告訴 Bob 這些猜測裡面至少有 k 個猜測的結果為 true 。

給你二維整數陣列 edges ，Bob 的所有猜測和整數 k ，請你返回可能成為樹根的 節點數目 。如果沒有這樣的樹，則返回 0。

題解（記憶化遞迴）

這是換根 DP 問題，這道題相對簡單了，只要掌握圖的基本結構和遞迴的基本思想就能實現。

首先是建圖的部分，顯然 edges 是無向圖，guesses 是有向圖。我們的演演算法基本框架應該是：列舉每個根節點，計算 guesses 中猜測正確的邊的個數，如果猜測次數 ≥ k 則記錄 1 次結果。現在的問題是如果優化查詢的時間複雜度，我們觀察依次從 0 到 n - 1 修改根節點會發生什麼？

我們發現： 每次調整中只有條邊的結構關係變化。比如從根 0 調整到根 1 時，只有 0 → 1 被修改為 1 → 0，而其他邊都沒有變化，存在重疊子結構 / 重疊子問題。

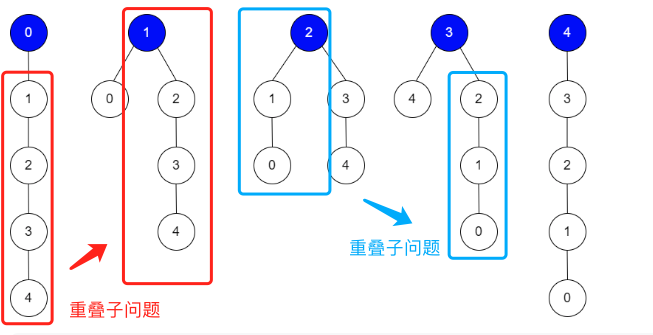
定義 $f(u, v)$ 表示在 u → v 的子結構中猜測正確的邊數，例如在範例 2 中，f(1, 2) = 1。顯然在已知 f(1,2) 的結果後，在以節點 1 為根節點的情況中不需要重複計算，達到了剪枝的目的。

編碼部分有兩個細節：

起點需要特殊處理，我們考慮起點是用 u → v 開始的子結構，起點 u 可以採用特殊值 $n$。
注意空間壓縮，顯然使用領接表比臨接矩陣更優。備忘錄可以使用移位壓縮，Key = u * mod + v，由於題目資料範圍是 10000，所以 mod 就取 100000。

class Solution {
    private val graph = HashMap<Int, MutableList<Int>>()
    private val guessGraph = HashMap<Int, MutableList<Int>>()

    fun rootCount(edges: Array<IntArray>, guesses: Array<IntArray>, k: Int): Int {
        // 無向圖
        for (edge in edges) {
            graph.getOrPut(edge[0]) { LinkedList<Int>() }.add(edge[1])
            graph.getOrPut(edge[1]) { LinkedList<Int>() }.add(edge[0])
        }
        // 有向圖
        for (guess in guesses) {
            // 過濾不存在邊（題目沒有這種用例）
            if (!graph.containsKey(guess[0]) || !graph[guess[0]]!!.contains(guess[1])) continue
            guessGraph.getOrPut(guess[0]) { LinkedList<Int>() }.add(guess[1])
        }
        val n = edges.size + 1
        // 空間溢位：val memo = Array(n + 1) { IntArray(n) { -1 } }
        val memo = HashMap<Long, Int>()
        var count = 0
        // 列舉所有根
        for (root in 0 until n) {
            if (dfs(memo, 100000, n, root) >= k) count++
        }
        return count
    }

    // 記憶化遞迴
    private fun dfs(memo: HashMap<Long, Int>, mod: Int, u: Int, v: Int): Int {
        // 空間壓縮
        val key = 1L * u * (mod) + v
        // 備忘錄
        if (memo.containsKey(key)) return memo[key]!!
        var count = 0
        for (to in graph[v]!!) {
            // 過濾指向父節點的邊
            if (to == u) continue
            // 檢查猜測
            if (guessGraph.containsKey(v) && guessGraph[v]!!.contains(to)) count++
            // 遞迴
            count += dfs(memo, mod, v, to)
        }
        memo[key] = count
        return count
    }
}

複雜度分析：

時間複雜度：$O(1)$ 其中 $n$ 是 $edges$ 陣列的長度，$m$ 是 $guesses$ 陣列的長度。建圖佔用 $O(n + m + 2n)$，在記憶化遞迴下每條邊的子結構最多存取 2 次，即總共有 2n 個子問題，所以查詢的複雜度是 $O(2n)$
空間複雜度：$O(n + m + 2*n)$ 建圖佔用 $O(n + m)$，備忘錄最多記錄 $n$ 條邊的兩個方向的子結構，遞迴棧最大為 $n$。

就說這麼多，今天單週賽加油