字首和與二維字首和

字首和

　　字首和，顧名思義，就是所有字首之和，給一個最基本的例子：

　　如圖，a為原始陣列，s為完成預處理後的陣列，很容易看出來s[ i ]=s[ i - 1 ]+a[ i ]，而也就是s[ i ]=a[1]+a[2]+……+a[ i ]，需要注意的是記s[0]=0。

　　那麼，如果我想要知道一個區間的區間和該怎麼做呢？其實很簡單，例如要求區間3~5的區間和，就可以用s[5]-s[2]=19-8=11。這裡同樣需要注意當減去區間左邊界時需要將其減1，及求l~r的區間和，是用s[ r ]-s[ l-1 ]。

　　根據以上求區間字首和的思路可以完成以下程式碼

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define MAXN 100010
 4 int n,m;
 5 int a[MAXN],s[MAXN];
 6 int main()
 7 {
 8     cin>>n; //陣列的長度 
 9     for(int i=1;i<=n;i++)
10     {
11         cin>>a[i];  
12         s[i]=s[i-1]+a[i]; //這裡就是上面講到的預處理的方法 
13     }
14     cin>>m; //讀入區間數量 
15     for(int i=1;i<=m;i++)
16     {
17         int l,r;
18         cin>>l>>r; //讀入區間的左邊界和右邊界 
19         cout<<s[r]-s[l-1]<<endl; //輸出區間和 
20     }
21     return 0;
22 } 

二維字首和

　　剛才介紹的一維字首和可以用來快速一維序列的區間總和，而二維字首和則可以快速求出一個二維矩陣中一個長方形內所以元素的總和。

　　在往下說之前我們依舊先來看一張圖：

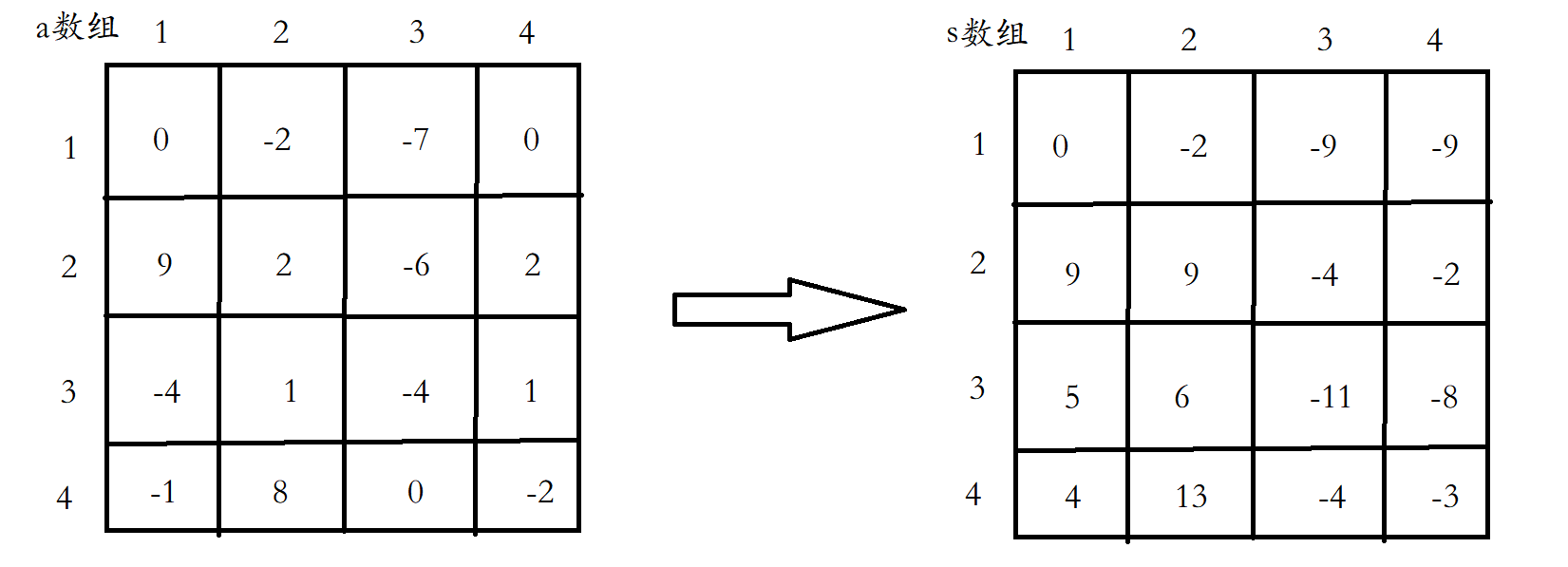
　　如圖，a為原始陣列，s為預處理過的陣列，它們之間有什麼規律嗎？乍一看似乎不怎麼看的出來，那就先看第一排和第一列，很容易就發現，這就是上面的字首和，下面再看s[2][2]，它與a[2][2]又有什麼聯絡呢？仔細看會發現s[2][2]=s[2][1]+s[1][2]+a[2][2]，那麼規律就是如此嗎？似乎並不對！那就在看一張圖：

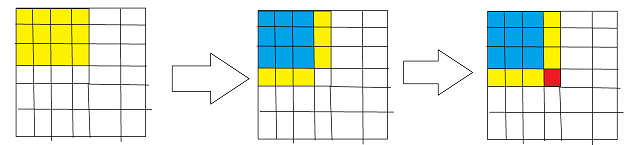
　　圖中，我們就可以看出在s[2][1]+s[1][2]相加後，會有一塊被重複加了兩次，所以，其實還要再減去一個s[1][1]，只不過因為s[1][1]=0，所以一時未發現，綜上，我們可以得到二維字首和預處理的方法，及s[ i ,j ]=s[ i,j-1 ]+s[ i-1,j ]-s[ i-1,j-1 ]+a[ i,j ]。

　　二維字首和程式碼與一維差別不大，再次便不贅述了其實是懶得打。

總結

　　利用字首和我們可以在常數時間中查詢區間和，這在某些方面是可以給程式帶來極大的幫助，而其中耗時相對較大的二維字首和在很多時候是可以轉換從一維字首和的做法的，此處留給讀者自行思考。

                                                                        碼字不易，點個讚唄§(*￣▽￣*)§