基於圖的路徑搜尋技術基礎知識
基於搜尋的路徑規劃
1.0 圖搜尋基礎
1.1 Configuration Space(設定空間)
Robot configuration
機器人設定,簡單來說就是將機器人在空間中用一個點來描述,忽略了其外觀資訊,例如形狀不管是圓形還是方形,都均會抽象成一個點進行表示。Robot degree of freedom (DOF)
在進行軌跡規劃的時候是要考慮機器人的一個實際的運動模型的,不同的運動模型需要的輸入和輸出變數是不同的,即對應的控制變數的維度是不同的,儘可能的使用一個較小的自由度去表示機器人在設定空間中的位姿。Robot configuration space
一個 \(n\) 維的空間,包含著機器人的所有可能位置,稱為C-Space- 簡單來說,每個機器人的位姿在
C-space中就是一個點而已。
1.2 C-space Obstacle
Planning in workspace
首選解釋一下什麼事工作空間即什麼是workspace,簡單來說其實就是機器人真實的一個工作空間,就是我們所處的物理世界。如果在物理世界中進行機器人的一個路徑規劃,其實是一個比較麻煩的事情,有如下兩個原因:- 每個機器人擁有不同的形狀和大小(different shape and size)
- 碰撞檢測需要指導機器人的幾何資訊
這樣進行規劃是非常耗時和困難的,因此引入C-space這一概念
Planning in C-space- 在
C-space中,機器人被抽象為了一個C-space中的一個點,例如三維空間中機器人可以由 position(a point in \(R^3\)),pose (a point in \(SO(3)\)) - 至於真實世界中感知到的障礙物資訊則需要提前展示部署到
C-space中去,是一個在規劃前要完成的工作,我們稱這些障礙物為C-space中的障礙物,或者稱為C-obstacle - \(C_{space} = (C_{obstacle})\ U\ (C_{free})\)
- 而我們通常所說的路徑規劃此時就可以說成是在
C-free中找一個連線 \(q_{start}\) 和 \(q_{goal}\) 的路徑
- 在
1.3 總結
-
In workspace
機器人是一個擁有形狀和大小的實體 (hard for motion planning) -
In configuration space
- 機器人是一個點 (easy for motion planning)
- 障礙物提前加入到
C-space中去,其實嚴格上來說也不算是加入,只是以某種方式對規劃時使用的地圖進行了一定方式的變動,使得在後續的路徑規劃中可以忽略機器人的一個形狀和大小的約束,從而簡化規劃問題的難度。
-
在
C-space表示障礙物可能非常複雜。 因此在實踐中使用了近似(但更保守)的表示,例如下圖所示是將機器人通建模為一個半徑為 \(r\) 的球形:
2.0 圖和搜尋技術
2.1 圖
-
首先圖這個概念相信大家或多或少的在本科學習中都會接觸到圖論相關的內容,簡單來說圖是由節點和邊構成的。根據節點和邊的不同形式還可以分成無向圖,有向圖,賦權圖等等。下面是一些例子。
-
無向圖
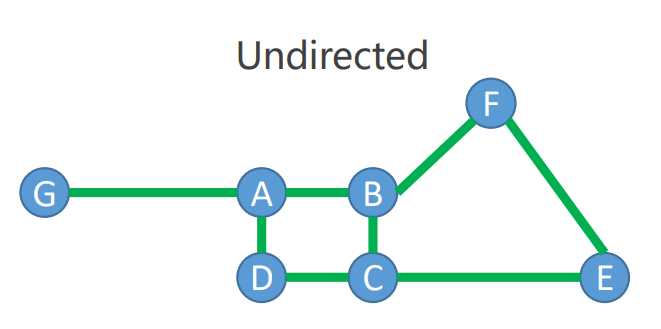
-
有向圖
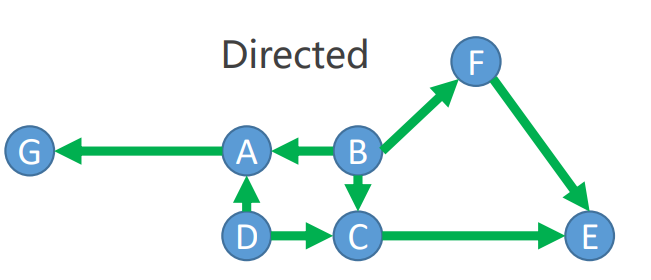
-
賦權圖

-
-
狀態空間圖 (
state sapce graph)
搜尋演演算法的數學表示,即將一張圖抽象成數學上的表達形式- 對於每一個搜尋問題,都有一個對應的
state space graph - 圖中節點之間的聯絡自然由連結兩個節點之間的邊所表示
- 下面兩張圖分別代表了在基於柵格地圖搜尋是和基於概率路線圖搜尋是所對應的
state space graph
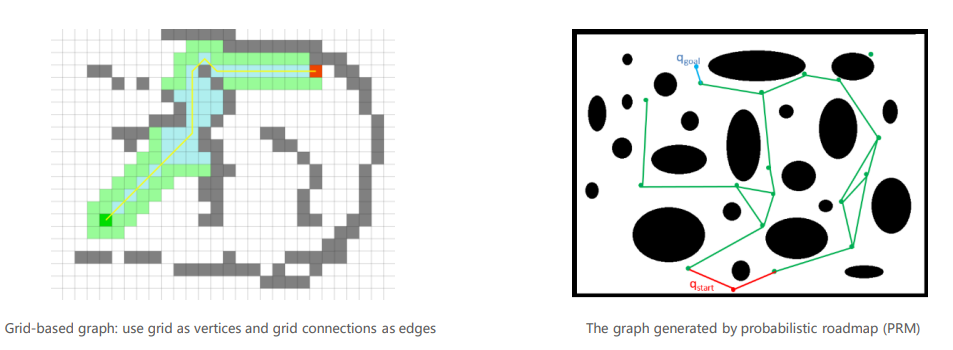
- 對於每一個搜尋問題,都有一個對應的
2.2 圖搜尋概述
- 圖搜尋技術總是從一個起點 \(X_S\) 出發
- 可以將搜尋圖畫成一顆樹(資料結構中的樹),樹的父節點就是起點
- 然後對該樹進行遍歷,當在樹中找到目標點的時候,通過該節點進行回溯,即可找到一條從起點到終點的路徑。
- 然而對於許多問題,我們永遠無法真正構建整棵樹,太大或效率低下——我們只想儘快到達目標節點。
- 下面展示的則是一個簡單的將圖轉換為樹的過程
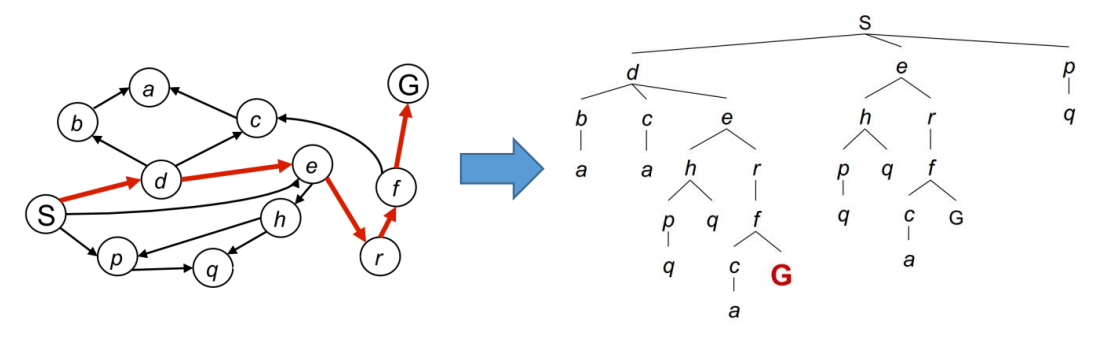
一個基於圖搜尋的大致流程可以歸結為如下步驟
- 維持一個 container 去儲存將要存取的節點
- container 初始化的時候只有 \(X_S\) 節點
- LOOP
- 從 container 中 Remove 一個節點,移除的規則需要遵循提前定義好的
score function- Visit a node
- Expansion: 獲得移除節點的鄰居節點
- Discover all its neighbors
- Push them (neighbors) into the container
- 從 container 中 Remove 一個節點,移除的規則需要遵循提前定義好的
- End LOOP
2.3 圖搜尋回顧
- Question 1: When to end the loop? 什麼時候終止上述的 LOOP
- Possible Option: 當所維護的 container 為空的時候
- Question 2: What if the graph is cyclic? 如果圖是迴圈的呢?
- 當一個節點從容器中移除(擴充套件/存取)時,它不應該再次新增回容器。
- Question 3: 以什麼方式刪除正確的節點,以便儘快達到目標狀態,從而減少圖節點的擴充套件。
\(\quad\)顯而易見,問題3則是解決圖搜尋問題或者說基於搜尋的路徑規劃問題的核心問題,起初,我們並不知道目標點在圖中的哪個位置,因此我們只能嘗試去遍歷圖中的所有節點,當到達目標節點的時候則停止遍歷即可,那麼下面的一個問題則變成了如何高效的進行圖的遍歷,從而快速的找到目標點。
2.4 圖的遍歷 (Graph Traversal)
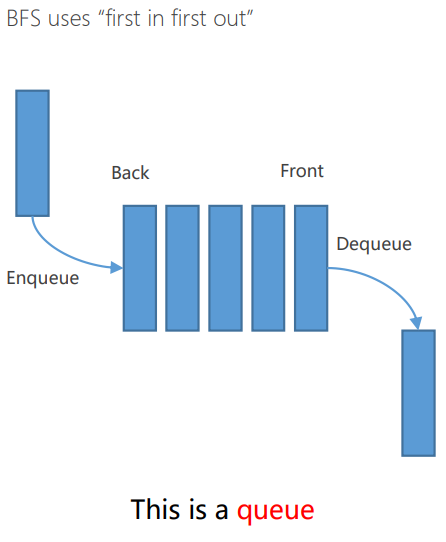
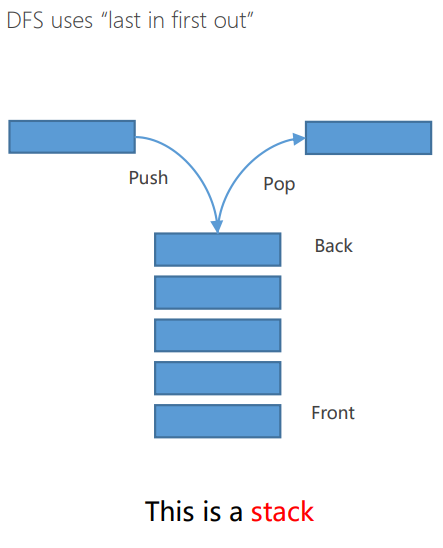
\(\quad\)學過一點關於圖論的同學可能知道,圖的遍歷遍歷一般是基於兩種方法,即我們通常所說的深度優先遍歷(DFS)和廣度優先遍歷(BFS),兩者的遍歷方式有一定的區別,首先在程式設計實現的時候,所對應的資料結構一個對應的是堆,一個對應的則是棧,具體如下圖所示:
2.4.1 Depth First Search (DFS)
\(\quad\)策略:移除/擴充套件容器中深度最大的節點,若深度一樣,則根據自定義的策略進行選擇移除(即後文所說的 Heuristic Function)
\(\quad\)具體的實現如下圖所示,維護一個 last in first output container (i.e. statck)
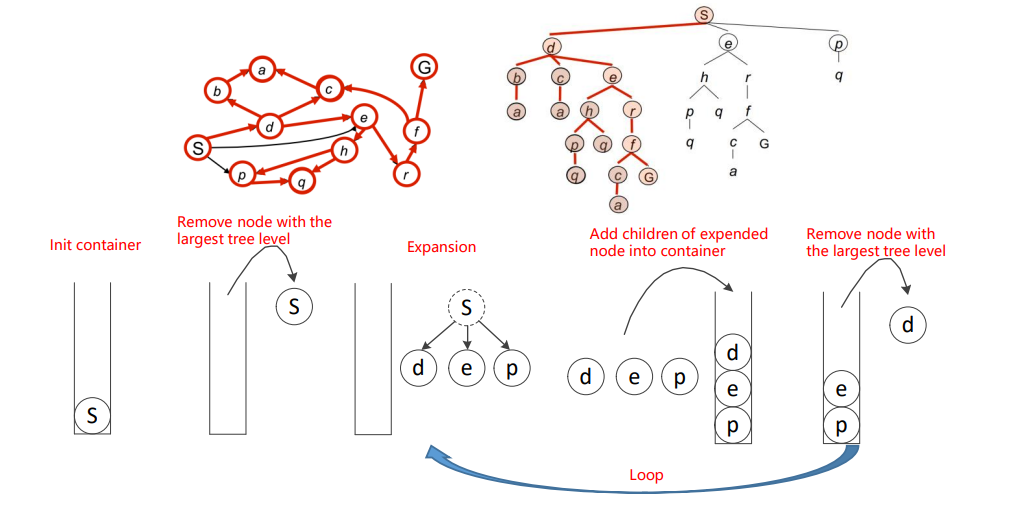
\(\quad\)下面通過一個動圖來展示這一過程,根據圖中的編號,節點會依次的進行擴充套件和遍歷。

2.4.2 Breadth First Search (BFS)
\(\quad\)廣度優先搜尋的策略:移除/擴充套件容器中最淺層的節點。
\(\quad\)實現方式:維護一個 first in first output container (i.e. queue)
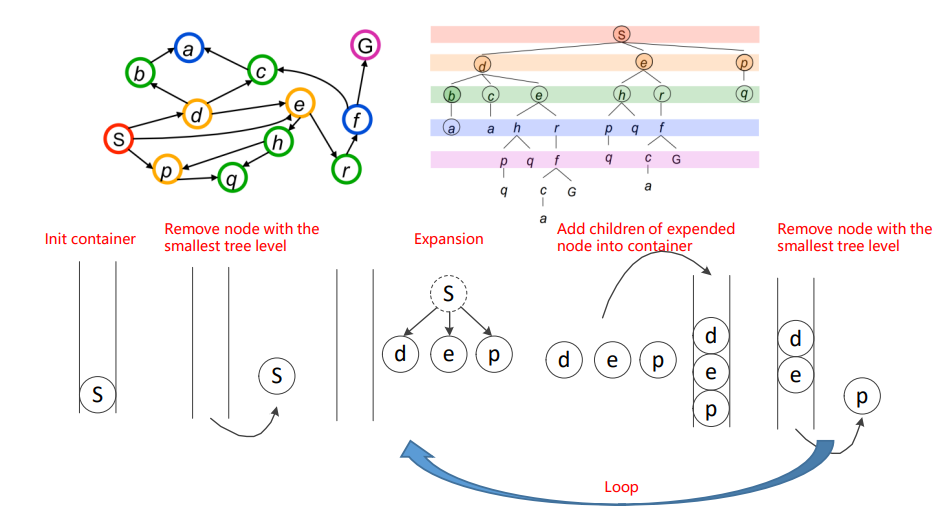
\(\quad\)下面通過一個動圖來展示這一過程,根據圖中的編號,節點會依次的進行擴充套件和遍歷。

2.4.3 BFS VS DFS
- BFS 和 DFS 的對比如下圖所示:

\(\quad\) 從圖中可以明顯的看到雖然兩個方法都可以找到最終的目標點,但是 DFS 明顯找到的不是最優解,即並不是最短路。這裡我們只是直觀上說明 DFS 不能找到最優路徑,事實上也確實不行因此在後面的討論中,我們值討論基於 BFS 的遍歷方式。
3.0 啟發式搜尋 (Heuristic Search)
3.1 貪心搜尋
\(\quad\) BFS 和 DFS 在選擇下一個節點的時候,僅僅是依靠當前 container 中誰是 "first in" 或者誰是 last in 進行判斷。
\(\quad\) 貪婪演演算法進行搜尋則是根據一種 heuristic function 進行選擇,從而選擇認為(最好的節點)
-
Heuristic Definition:
A heuristic is a guess of how close to you are to the target。即啟發式是一個對當前點距離目標點多遠的猜測,那麼我們自然就可以使用兩點之間的一個正規化距離來判斷猜測了,下圖就表示了利用歐式距離和曼哈頓距離當作 heuristic 時所猜測的距離。

heuristic 應當滿足以下兩點:
-
啟發式搜尋可以指導你朝著一個儘可能正確的方向向目標點靠近。
-
啟發式函數應當是非常簡單進行計算的,因為本身我們在不使用啟發式搜尋時,單單通過廣度優先遍歷是可以找到一個起點到目標點的最有解的,但是其速度比較慢,因此才加入啟發式搜尋,但如果啟發式函數計算較為複雜,反而會增加計算時間,得不償失,啟發式搜尋也就是去了意義。
\(\quad\) 下面對 BFS 和 Greedy Best-First Search 通過一張動圖進行簡單對比(環境過於簡單,起點和終點之間沒有障礙物)。
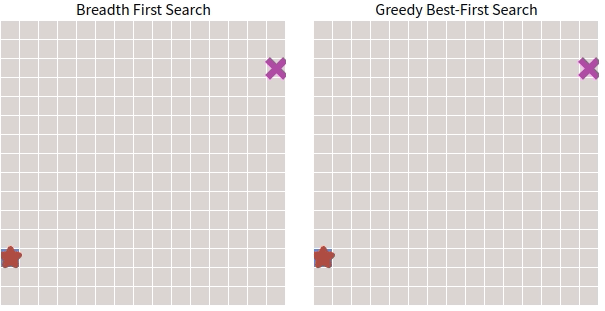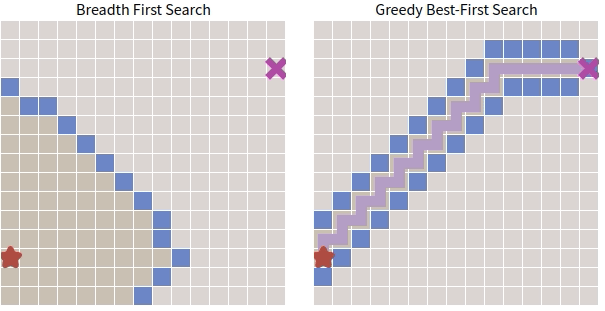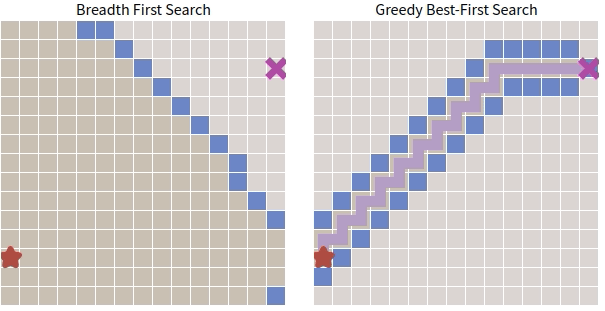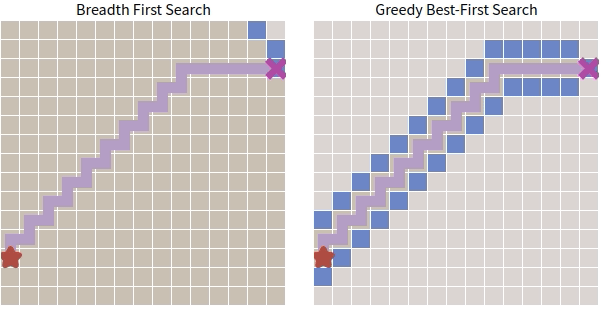
\(\quad\) 看起來貪心搜尋的表現確實不錯。接下來看看如果在圖中加入障礙物會怎麼樣。
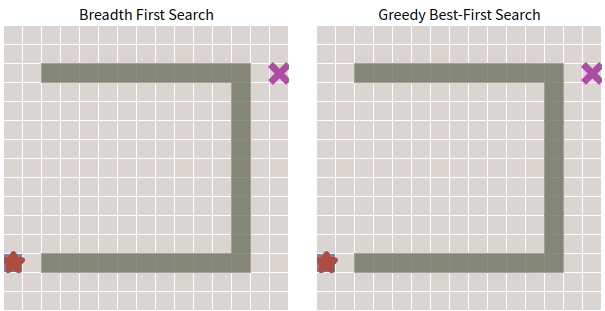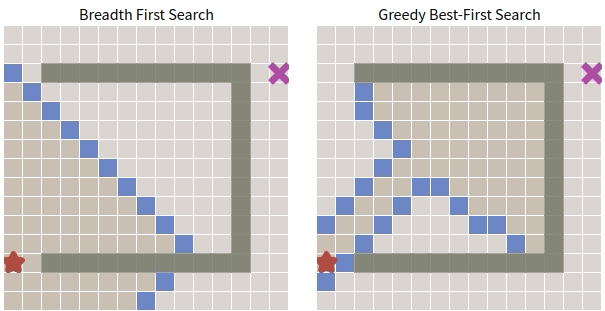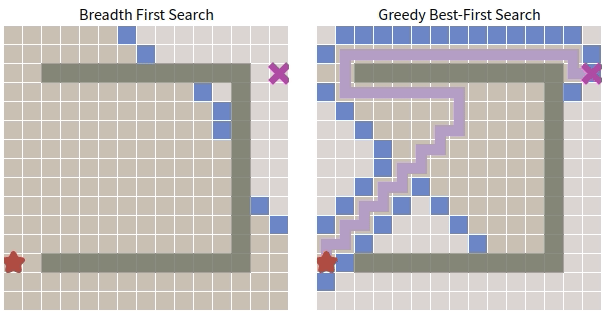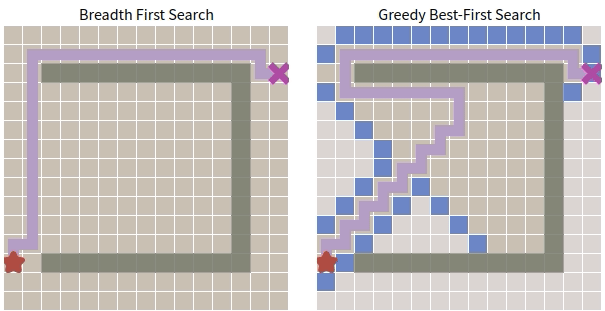
\(\quad\) 很遺憾,貪心搜尋失敗了,並沒有找到最優路徑,太過於注重眼前利益。
\(\quad\) 導致這種問題i的原因是什麼呢?在接下來的討論中揭曉。
Reference
- https://cs.stanford.edu/people/abisee/tutorial/bfsdfs.html
- https://www.redblobgames.com/pathfinding/a-star/introduction.html