深度學習-RNN

I.前言

介紹RNN的概念和應用

RNN（Recurrent Neural Network，迴圈神經網路）是一類能夠處理序列資料的神經網路，它在處理時考慮了之前的狀態，因此能夠對序列資料中的每個元素進行建模和預測。
RNN的應用非常廣泛，特別是在自然語言處理和時間序列分析方面。以下是RNN在各個領域的應用：
自然語言處理（NLP）
文字分類：將文字歸類到不同的類別中，如情感分析、垃圾郵件過濾、新聞分類等。
機器翻譯：將一種語言的文字翻譯成另一種語言的文字。
語音識別：將人類語音轉化為文字。
文字生成：根據給定的文字生成新的文字，如對話生成、詩歌生成等。
問答系統：回答使用者的自然語言問題。
時間序列分析
時序預測：根據過去的資料預測未來的資料，如股票價格預測、氣溫預測等。
行為識別：根據感測器資料識別人的行為，如健身追蹤、手勢識別等。
異常檢測：識別與正常行為不同的行為或異常行為，如網路入侵檢測、裝置故障檢測等。
除此之外，RNN還可以用於影象和視訊處理等領域。

II. RNN基礎

RNN的概念和結構

RNN（Recurrent Neural Network，迴圈神經網路）是一種可以對序列資料進行建模的神經網路。相比於傳統神經網路，RNN增加了迴圈連線，使得網路可以處理序列資料中的時序資訊。

RNN的結構包含了一個迴圈單元，可以看做是對於前一時刻的狀態 \(h_{t-1}\) 和當前時刻的輸入 \(x_t\) 的函數，即 \(h_t=f(h_{t-1},x_t)\)，其中 \(f\) 為非線性的啟用函數。通過這種方式，RNN可以在處理當前輸入的同時，記憶之前輸入的資訊，即將上一時刻的狀態作為當前時刻的輸入。

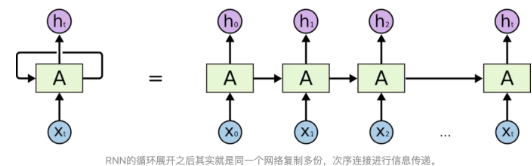
下圖是一個簡單的RNN結構示意圖，其中 \(x_t\) 為輸入，\(h_t\) 為當前時刻的狀態，\(y_t\) 為輸出：

在每個時間步中，輸入 \(x_t\) 會與上一時刻的狀態 \(h_{t-1}\) 經過一個帶有權重矩陣 \(U\) 和 \(W\) 的線性變換，然後通過啟用函數 \(f\) 得到當前時刻的狀態 \(h_t\)。接下來，\(h_t\) 會作為下一時刻的輸入狀態 \(h_{t+1}\)，並與下一時刻的輸入 \(x_{t+1}\) 經過相同的變換和啟用函數，直到所有時刻的輸入都處理完成。

最終，我們可以通過將所有時刻的狀態 \(h_1,h_2,...,h_T\) 經過一個帶有權重矩陣 \(V\) 的線性變換，再通過啟用函數得到每個時刻的輸出 \(y_1,y_2,...,y_T\)。輸出的具體形式取決於具體的任務，如分類任務通常使用 Softmax 啟用函數，而回歸任務則使用線性啟用函數。

RNN的前向傳播和反向傳播演演算法

RNN的前向傳播和反向傳播演演算法是神經網路訓練的核心。在前向傳播演演算法中，我們將輸入序列逐步輸入到網路中，並計算每個時刻的輸出；在反向傳播演演算法中，我們通過比較網路輸出和真實標籤之間的誤差，計算每個引數對誤差的貢獻，並使用梯度下降演演算法來更新引數。

前向傳播演演算法

假設我們的輸入序列為 \(x_{1:T}={x_1,x_2,...,x_T}\)，其中 \(x_t\) 表示第 \(t\) 個時刻的輸入向量。我們使用 \(h_t\) 表示第 \(t\) 個時刻的隱藏狀態向量，\(y_t\) 表示第 \(t\) 個時刻的輸出向量。

在前向傳播演演算法中，我們首先將第一個時刻的輸入向量 \(x_1\) 與初始狀態 \(h_0\) 輸入到網路中，通過一個線性變換和啟用函數計算出第一個時刻的隱藏狀態 \(h_1\)，然後再將 \(h_1\) 和第二個時刻的輸入向量 \(x_2\) 輸入到網路中，依次計算出第二個時刻到第 \(T\) 個時刻的隱藏狀態 \(h_2,h_3,...,h_T\) 和輸出向量 \(y_1,y_2,...,y_T\)。具體的計算方式如下：

\(h_t = f(U_{xt} + Wh_{t-1}+b_h)\)

\(y_t=g(Vh_t + b_y)\)

其中，\(U\)、\(W\)、\(V\) 分別為輸入、隱藏狀態和輸出的權重矩陣，\(b_h\) 和 \(b_y\) 分別為隱藏狀態和輸出的偏置向量，\(f\) 和 \(g\) 分別為隱藏狀態和輸出的啟用函數。

反向傳播

首先，我們需要根據當前時刻的輸出向量 \(y_t\) 和真實標籤 \(y_t^\prime\) 計算輸出向量的梯度 \(\frac{\partial L}{\partial y_t}\)，其中 \(L\) 表示損失函數。具體來說，如果我們使用平方損失函數，那麼輸出向量的梯度可以表示為：

\[\frac{\partial L}{\partial y_t} = 2(y_t - y_t^\prime) \]

接下來，我們需要利用反向傳播演演算法依次計算每個時刻的隱藏狀態向量 \(h_t\) 和輸入向量 \(x_t\) 的梯度 \(\frac{\partial L}{\partial h_t}\)、\(\frac{\partial L}{\partial x_t}\)。具體來說，對於某個時刻 \(t\)，我們可以通過下面的公式計算隱藏狀態向量 \(h_t\) 的梯度：

\[\frac{\partial L}{\partial h_t} = \frac{\partial L}{\partial y_t} \cdot W_{hy}^T + \frac{\partial L}{\partial h_{t+1}} \cdot W_{hh}^T \]

其中 \(W_{hy}\) 和 \(W_{hh}\) 分別表示輸出層到隱藏層和隱藏層到隱藏層的權重矩陣。需要注意的是，在最後一個時刻 \(T\)，我們需要將 \(\frac{\partial L}{\partial h_{T+1}}\) 設定為零向量。

接著，我們可以利用隱藏狀態向量的梯度 \(\frac{\partial L}{\partial h_t}\) 計算輸入向量 \(x_t\) 的梯度 \(\frac{\partial L}{\partial x_t}\)。具體來說，對於某個時刻 \(t\)，我們可以通過下面的公式計算輸入向量 \(x_t\) 的梯度：

\[\frac{\partial L}{\partial x_t} = \frac{\partial L}{\partial h_t} \cdot W_{xh}^T \]

其中 \(W_{xh}\) 表示輸入層到隱藏層的權重矩陣。

最後，我們可以利用輸出向量的梯度 \(\frac{\partial L}{\partial y_t}\)、隱藏狀態向量的梯度 \(\frac{\partial L}{\partial h_t}\) 和輸入向量的梯度 \(\frac{\partial L}{\partial x_t}\) 對模型引數進行更新。具體來說，我們可以採用梯度下降演演算法或者其他優化演演算法來更新權重矩陣和偏置向量，以便更好地訓練模型。

需要注意的是，在實際應用中，我們可能需要對學習率進行動態調整，以便更好地訓練模型。此外，在實現反向傳播演演算法時，我們通常需要採用遞迴或者回圈的方式進行計算，以便有效地利用歷史資訊。

RNN的變種：LSTM和GRU

除了標準的RNN，還有兩種常見的變種RNN，分別是長短期記憶網路（LSTM）和門控迴圈單元（GRU）。這兩種變種網路都是在標準RNN的基礎上進行改進，旨在解決標準RNN中出現的梯度消失或爆炸問題，並能夠更好地捕捉序列中的長期依賴關係。

LSTM

長短期記憶網路（LSTM）是由Hochreiter和Schmidhuber在1997年提出的。LSTM的主要改進在於引入了三個門機制：輸入門、遺忘門和輸出門。LSTM的核心思想是通過這三個門控制資訊的流動，從而更好地維護序列中的長期依賴關係。

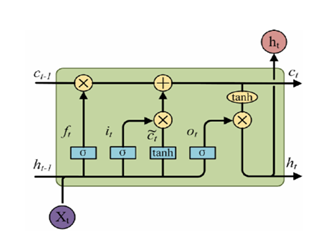
具體來說，輸入門控制新資訊的輸入，遺忘門控制之前的資訊是否需要被遺忘，輸出門控制輸出的資訊。這三個門的計算方式都包含了一個sigmoid函數，用於將輸入對映到0-1之間的範圍。LSTM的結構如下圖所示：

其中，圓圈表示神經元，箭頭表示資訊的傳遞。綠色方框表示輸入門，紅色方框表示遺忘門，黃色方框表示輸出門。

LSTM的前向傳播和反向傳播演演算法與標準RNN類似，只是在計算中要加上門機制的計算。

GRU

門控迴圈單元（GRU）是由Cho等人在2014年提出的。相比於LSTM，GRU更為簡單，只包含了兩個門機制：重置門和更新門。GRU的計算複雜度較低，訓練速度也更快，而且在某些任務中效能表現與LSTM相當甚至更好。

GRU的結構如下圖所示：

其中，綠色方框表示重置門，藍色方框表示更新門。GRU的前向傳播和反向傳播演演算法也與標準RNN類似，只是在計算中要加上門機制的計算。

總的來說，LSTM和GRU都是為了解決標準RNN中的梯度消失或爆炸問題，並能夠更好地捕捉序列中的長期依賴關係而提出的。兩者的計算複雜度都比標準RNN高，但在某些

III. RNN的應用

自然語言處理中的RNN應用：文字分類、情感分析、機器翻譯等

1. 文字分類

文字分類是將文字分為不同類別的任務，例如將新聞文章分為體育、政治、娛樂等類別。RNN可以通過學習文字的序列資訊，對文字進行分類。具體地，可以將文字的每個單詞或字元依次輸入到RNN中，最後通過全連線層進行分類。

2. 情感分析

情感分析是對文字進行情感判斷的任務，例如判斷一篇文章是正面的、負面的還是中性的。RNN可以通過學習文字的上下文資訊，對文字中的情感進行分析。具體地，可以將文字的每個單詞或字元依次輸入到RNN中，最後通過全連線層輸出情感分類結果。

3. 機器翻譯

機器翻譯是將一種語言的文字自動翻譯成另一種語言的任務。RNN在機器翻譯中的應用主要是seq2seq模型，它將源語言文字編碼成一個向量，然後將該向量作為目標語言文字的初始狀態，並逐步生成目標語言的詞語序列。具體地，seq2seq模型包含編碼器和解碼器兩個部分，其中編碼器是一個RNN，用於編碼源語言文字，而解碼器也是一個RNN，用於生成目標語言的詞語序列。

時間序列分析中的RNN應用：時序預測、異常檢測、行為識別等

1. 時序預測

時序預測是根據歷史資料預測未來資料的任務。RNN可以通過學習歷史時序資料的序列資訊，對未來時序資料進行預測。具體地，可以將歷史時序資料作為輸入序列，將未來時序資料作為輸出序列，通過訓練RNN模型，使得模型能夠對未來時序資料進行預測。

2. 異常檢測

異常檢測是識別時間序列中不同於正常模式的資料點的任務。RNN可以通過學習時間序列資料的模式，對異常點進行識別。具體地，可以將時間序列資料輸入到RNN中，通過訓練模型，使得模型能夠對正常模式進行建模，從而識別不同於正常模式的資料點。

3. 行為識別

行為識別是識別時間序列資料中的行為或動作的任務。RNN可以通過學習時間序列資料的序列資訊，對不同的行為或動作進行識別。具體地，可以將時間序列資料作為輸入序列，通過訓練RNN模型，使得模型能夠對不同的行為或動作進行分類。

IV. RNN的進階應用

注意力機制和Seq2Seq模型

注意力機制和Seq2Seq模型是RNN在自然語言處理中應用的兩個重要領域。

1. 注意力機制

在處理長序列輸入時，傳統的RNN模型往往會出現梯度消失或梯度爆炸的問題，導致模型難以學習到長期依賴關係。為了解決這個問題，注意力機制被引入到RNN中。注意力機制可以讓模型在處理長序列輸入時，將注意力集中在與當前任務相關的部分，從而提高模型的效能。

具體地，注意力機制通過對輸入序列中不同位置的資訊進行加權，來構建一個加權和向量，使得模型能夠關注與當前任務相關的資訊。在RNN中，通常使用雙向RNN或者門控RNN結構與注意力機制相結合，從而能夠更好地處理長序列輸入。

2. Seq2Seq模型

Seq2Seq模型是一種用於序列到序列轉換任務的模型，如機器翻譯、對話系統等。它由兩個RNN模型組成，分別是編碼器和解碼器。編碼器將源語言的序列輸入，輸出一個固定維度的向量作為上下文資訊，解碼器根據上下文資訊以及目標語言的上一個單詞，逐步生成目標語言的序列。

在Seq2Seq模型中，編碼器和解碼器通常採用門控RNN結構，如LSTM和GRU。同時，注意力機制也被廣泛應用於Seq2Seq模型中，用於提高模型的效能。通過注意力機制，模型能夠在解碼過程中動態地將注意力集中在輸入序列的不同部分，從而能夠更好地處理長序列輸入。

多層RNN和雙向RNN

1. 多層RNN

多層RNN由多個RNN層堆疊而成，每個RNN層的輸出都作為下一層RNN的輸入。多層RNN可以增加模型的複雜度，提高模型的表達能力。在處理複雜的任務時，多層RNN往往能夠比單層RNN取得更好的效能。

在多層RNN中，可以使用不同的RNN變種，如LSTM和GRU等。同時，為了防止梯度消失或梯度爆炸的問題，可以採用梯度裁剪等方法來調整梯度大小。

2. 雙向RNN

雙向RNN是由兩個RNN組成的模型，分別是前向RNN和後向RNN。前向RNN從輸入序列的第一個元素開始，逐步向後處理；後向RNN則從輸入序列的最後一個元素開始，逐步向前處理。最後，前向RNN和後向RNN的輸出會被合併起來，形成最終的輸出。

雙向RNN能夠更好地捕捉輸入序列中的上下文資訊，從而提高模型的效能。在自然語言處理中，雙向RNN經常被用於詞性標註、命名實體識別等任務。

RNN和CNN的結合

RNN和CNN是兩種常見的神經網路模型，分別在自然語言處理和影象處理等領域中得到廣泛應用。為了更好地利用它們各自的優勢，研究人員開始探索將它們結合起來的方法。

一種常見的RNN和CNN結合的方法是使用折積神經網路(Convolutional Neural Network, CNN)提取文字或影象的區域性特徵，再使用迴圈神經網路(Recurrent Neural Network, RNN)對這些特徵進行全域性建模。

具體來說，在文書處理中，可以先使用CNN提取出文字中的n-gram特徵，並將這些特徵轉換成定長的向量表示。然後，將這些向量輸入到RNN中，讓RNN學習文字中的長期依賴關係。

在影象處理中，可以使用CNN提取影象的區域性特徵，得到一系列的折積特徵圖。然後，將這些特徵圖輸入到RNN中，讓RNN學習影象中的長期依賴關係。

RNN和CNN的結合能夠更好地處理序列資料和區域性特徵，從而提高模型的效能。在實際應用中，需要根據具體的任務和資料情況選擇合適的模型結構和引數設定。

V. RNN的調參和優化

學習率、正則化和丟棄等技術

1. 學習率(Learning Rate)

學習率是指在每次迭代中更新模型引數時所採用的步長大小。過大的學習率可能導致模型引數在迭代過程中來回擺動，收斂速度慢或不收斂；過小的學習率則可能導致模型收斂速度過慢。通常需要對學習率進行適當的調整，可以使用學習率衰減等技術。

2. 正則化(Regularization)

正則化是指在損失函數中加入一些懲罰項，以避免過擬合。常見的正則化方法包括L1正則化、L2正則化和dropout等。

L1正則化通過在損失函數中新增權重係數的絕對值之和來懲罰過大的權重，可以促使模型學習到更稀疏的特徵。

L2正則化通過在損失函數中新增權重係數的平方和來懲罰過大的權重，可以促使模型學習到較小的權重，從而避免過擬合。

dropout是一種在網路層之間隨機丟棄一些節點的技術，可以使得模型在訓練過程中不依賴於特定的節點，從而提高模型的魯棒性。

3. 丟棄(Dropout)

丟棄是一種在神經網路中隨機丟棄一些神經元的技術，可以減輕過擬合的問題。在訓練過程中，每個神經元都有一定的概率被丟棄，這樣可以強制模型學習到更加魯棒的特徵，從而提高模型的泛化能力。

梯度消失和梯度爆炸問題

在訓練深度神經網路（DNN）時，梯度消失和梯度爆炸問題是常見的挑戰之一。這些問題同樣存在於RNN中，因為RNN的網路結構導致了梯度在反向傳播時會反覆相乘。這可能導致在網路深度增加時，梯度變得非常小（梯度消失）或非常大（梯度爆炸），從而使網路難以訓練。

梯度消失問題通常是由於在反向傳播中反覆相乘的梯度很小，導致在早期層的引數更新幾乎不起作用。為了解決這個問題，可以使用不同的啟用函數（例如ReLU、LeakyReLU、ELU等）來代替傳統的sigmoid函數，因為這些函數在輸入的某些範圍內有更大的梯度。此外，可以使用LSTM或GRU等具有更少引數的RNN變體，以避免在長時間序列上的梯度消失問題。

梯度爆炸問題通常是由於在反向傳播中梯度反覆相乘的結果變得非常大，導致權重更新非常大，網路無法收斂。為了解決這個問題，可以使用梯度截斷技術，通過設定閾值來限制梯度的最大值。

此外，正則化和dropout等技術也可以用於避免過擬合和減少梯度消失問題的影響。

RNN的優化演演算法：Adam、Adagrad、RMSprop等

1. AdaGrad演演算法是梯度下降法的改進演演算法，其優點是可以自適應學習率。該優化演演算法在較為平緩處學習速率大，有比較高的學習效率，在陡峭處學習率小，在一定程度上可以避免越過極小值點。
2. AdaGrad演演算法雖然解決了學習率無法根據當前梯度自動調整的問題，但是過於依賴之前的梯度，在梯度突然變化無法快速響應。RMSProp演演算法為了解決這一問題，在AdaGrad的基礎上新增了衰減速率引數。也就是說在當前梯度與之前梯度之間新增了權重，如果當前梯度的權重較大，那麼響應速度也就更快
3. Adam優化演演算法是在RMSProp的基礎上增加了動量。有時候通過RMSProp優化演演算法得到的值不是最優解，有可能是區域性最優解，引入動量的概念時，求最小值就像一個球從高處落下，落到區域性最低點時會繼續向前探索，有可能得到更小的值

VI. 實踐：用Python實現RNN

使用PyTorch實現一個簡單的RNN模型

1. 匯入PyTorch和其他必要的庫

import torch
import torch.nn as nn
import numpy as np

2. 定義RNN模型

class RNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(RNN, self).__init__()

        self.hidden_size = hidden_size
        self.i2h = nn.Linear(input_size + hidden_size, hidden_size)
        self.i2o = nn.Linear(input_size + hidden_size, output_size)
        self.softmax = nn.LogSoftmax(dim=1)

    def forward(self, input, hidden):
        combined = torch.cat((input, hidden), 1)
        hidden = self.i2h(combined)
        output = self.i2o(combined)
        output = self.softmax(output)
        return output, hidden

    def initHidden(self):
        return torch.zeros(1, self.hidden_size)

上面的程式碼定義了一個簡單的RNN模型，該模型接受一個輸入向量和一個隱藏狀態向量，並輸出一個預測向量和一個更新後的隱藏狀態向量。

在init函數中，我們定義了輸入到隱藏層和輸入到輸出層的線性變換，並將輸出層的輸出通過LogSoftmax進行歸一化處理。

在forward函數中，我們首先將輸入和隱藏狀態向量進行拼接，然後將拼接後的向量傳遞給線性變換，並通過LogSoftmax輸出預測結果。

在initHidden函數中，我們初始化隱藏狀態向量為全0向量。

3. 定義訓練函數

def train(inputs, targets, rnn):
    hidden = rnn.initHidden()

    rnn.zero_grad()

    loss = 0

    for i in range(len(inputs)):
        output, hidden = rnn(inputs[i], hidden)
        loss += criterion(output, targets[i])

    loss.backward()

    for p in rnn.parameters():
        p.data.add_(-learning_rate, p.grad.data)

    return output, loss.item()

上面的程式碼定義了一個訓練函數，該函數接受輸入和目標序列以及RNN模型作為引數，並返回模型的輸出和損失。

在訓練過程中，我們首先初始化隱藏狀態向量，並將模型的梯度清零。然後我們遍歷輸入序列，並將每個輸入向量和隱藏狀態向量傳遞給RNN模型，計算預測結果並累加損失。最後，我們計算損失的梯度，並使用隨機梯度下降更新模型的引數。

4. 定義資料集和超引數

pythonCopy codeinput_size = 4
hidden_size = 10
output_size = 3
learning_rate = 0.1

inputs = [torch.randn(1, input_size) for _ in range(5)]
targets = [torch.randint(0, output_size, (1,)).long() for _ in range(5)]

criterion = nn.NLLLoss()
rnn = RNN(input_size, hidden_size, output_size)

5. 定義優化器和損失函數

我們使用Adam優化器來更新模型的引數，並使用交叉熵損失函數作為模型的損失函數。在PyTorch中，可以通過torch.optim.Adam和nn.CrossEntropyLoss分別定義優化器和損失函數。

import torch.optim as optim
import torch.nn as nn

# 定義優化器和損失函數
optimizer = optim.Adam(model.parameters(), lr=0.01)
criterion = nn.CrossEntropyLoss()

6. 訓練模型

在訓練模型之前，我們需要先定義一些超引數，例如訓練輪數、批次大小等。我們還需要在每個訓練輪次結束後計算模型在驗證集上的準確率，以便及時發現過擬合的情況。

# 定義超引數
num_epochs = 10
batch_size = 64
learning_rate = 0.01

# 訓練模型
for epoch in range(num_epochs):
    # 訓練集迭代器
    train_iter.init_epoch()
    for batch_idx, batch in enumerate(train_iter):
        # 獲取資料和標籤
        data = batch.text
        target = batch.label - 1

        # 前向傳播
        output = model(data)

        # 計算損失
        loss = criterion(output, target)

        # 反向傳播
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        # 列印訓練資訊
        if batch_idx % 100 == 0:
            print('Epoch: {}, Batch: {}, Loss: {:.4f}'.format(epoch+1, batch_idx+1, loss.item()))

    # 驗證集迭代器
    val_iter.init_epoch()

    # 計算驗證集準確率
    correct = 0
    total = 0
    with torch.no_grad():
        for batch in val_iter:
            data = batch.text
            target = batch.label - 1

            output = model(data)

            _, predicted = torch.max(output.data, 1)

            total += target.size(0)
            correct += (predicted == target).sum().item()

    accuracy = correct / total
    print('Validation Accuracy: {:.2f}%'.format(accuracy*100))

7. 測試模型

訓練完成後，我們可以使用測試集來測試模型的效能。

# 測試集迭代器
test_iter.init_epoch()

# 計算測試集準確率
correct = 0
total = 0
with torch.no_grad():
    for batch in test_iter:
        data = batch.text
        target = batch.label - 1

        output = model(data)

        _, predicted = torch.max(output.data, 1)

        total += target.size(0)
        correct += (predicted == target).sum().item()

accuracy = correct / total
print('Test Accuracy: {:.2f}%'.format(accuracy*100))

至此，我們使用PyTorch實現了一個簡單的RNN模型，用於文字分類任務。在實際應用中，我們可以通過改變模型結構和超引數的設定來進一步優化模型的效能。

VII. 總結

RNN的優缺點

優點：

• 可以處理變長輸入序列，適用於序列資料建模。
• 具有記憶性，可以利用過去的資訊對當前的輸出進行預測。
• 可以實現共用引數，減少模型引數數量，節省計算資源。
• 可以通過堆疊多層RNN來增加模型深度，提高模型的表達能力。

缺點：

• 訓練過程中容易出現梯度消失或梯度爆炸問題，導致模型無法學習長期依賴關係。
• 訓練速度較慢，計算量較大，需要更多的計算資源和時間。
• 對於複雜的序列資料，可能需要使用更復雜的變種模型來處理，如LSTM和GRU。

總的來說，RNN適合處理序列資料，可以通過記憶歷史資訊來預測未來資料。但是它也存在著訓練困難和計算資源消耗較大等問題，需要根據具體情況進行選擇和優化。

VIII. 參考資料

書籍：

• Deep Learning by Goodfellow, Bengio, and Courville
• Neural Networks and Deep Learning by Michael Nielsen
• Hands-On Machine Learning with Scikit-Learn and TensorFlow by Aurélien Géron
• Recurrent Neural Networks with Python Quick Start Guide by Daniel Pyrathon
• Natural Language Processing with Python by Steven Bird, Ewan Klein, and Edward Loper

程式碼庫：

• PyTorch官方檔案：https://pytorch.org/docs/stable/nn.html
• TensorFlow官方檔案：https://www.tensorflow.org/api_docs/python/tf/keras/layers/GRU
• Keras官方檔案：https://keras.io/api/layers/recurrent_layers/