模型壓縮-剪枝演演算法詳解

一，前言
- 1.1，模型剪枝定義
二，深度神經網路的稀疏性
三，結構化稀疏
- 3.1，結構化稀疏分類
  - 3.1.1，channel 剪枝
  - 3.1.2，階段級別剪枝
- 3.2，結構化稀疏與非結構化稀疏比較
參考資料

一，前言

學術界的 SOTA 模型在落地部署到工業界應用到過程中，通常是要面臨著低延遲（Latency）、高吞吐（Throughpout）、高效率（Efficiency）挑戰的。而模型壓縮演演算法可以將一個龐大而複雜的預訓練模型轉化為一個精簡的小模型，從而減少對硬體的儲存、頻寬和計算需求，以達到加速模型推理和落地的目的。

近年來主流的模型壓縮方法包括：數值量化（Data Quantization，也叫模型量化），模型稀疏化（Model sparsification，也叫模型剪枝 Model Pruning），知識蒸餾（Knowledge Distillation）， 輕量化網路設計（Lightweight Network Design）和張量分解（Tensor Decomposition）。

其中模型剪枝是一種應用非常廣的模型壓縮方法，其可以直接減少模型中的引數量。本文會對模型剪枝的定義、發展歷程、分類以及演演算法原理進行詳細的介紹。

1.1，模型剪枝定義

模型剪枝（Pruning）也叫模型稀疏化，不同於模型量化對每一個權重引數進行壓縮，稀疏化方法是嘗試直接「刪除」部分權重引數。模型剪枝的原理是通過剔除模型中「不重要」的權重，使得模型減少引數量和計算量，同時儘量保證模型的精度不受影響。

二，深度神經網路的稀疏性

生物研究發現人腦是高度稀疏的。2016 年早期經典的剪枝論文 [1 ][1]曾提到，生理學上發現對於哺乳動物，嬰兒期產生許多的突觸連線，在後續的成長過程中，不怎麼用的那些突出會退化消失。而深度神經網路是模仿人類大腦的結構，所以說其也是存在稀疏的，這也是作者提出的模型剪枝方法的生理學上依據。因此，我們可以認為深度神經網路是存在稀疏性的。

根據深度學習模型中可以被稀疏化的物件，深度神經網路中的稀疏性主要包括權重稀疏，啟用稀疏和梯度稀疏。

2.1，權重稀疏

在大多數神經網路中，通過對網路層（折積層或者全連線層）對權重數值進行直方圖統計，可以發現，權重（訓練前/訓練後）的數值分佈很像正太分佈（或者是多正太分佈的混合），且越接近於 0，權重越多，這句是權重稀疏現象。

論文[1]認為，權重數值的絕對值大小可以看做重要性的一種度量，權重數值越大對模型輸出貢獻也越大，反正則不重要，刪去後模型精度的影響應該也比較小。

當然，影響較小不等於沒有影響，且不同型別、不同順序的網路層，在權重剪枝後影響也各不相同。論文[1]在 AlexNet 的 CONV 層和 FC 層的剪枝敏感性實驗，結果如下圖所示。

從圖中實驗結果可以看出，折積層的剪枝敏感性大於全連線層，且第一個折積層對剪枝最為敏感。論文作者推測這是因為全連線層本身引數冗餘性更大，第一個折積層的輸入只有 3 個通道所以比起他折積層冗餘性更少。

即使是移除絕對值接近於 0 的權重也會帶來推理精度的損失，因此為了恢復模型精度，通常在剪枝之後需要再訓練模型。典型的模型剪枝三段式工作 pipeline 流程和剪枝前後網路連線變化如下圖所示。

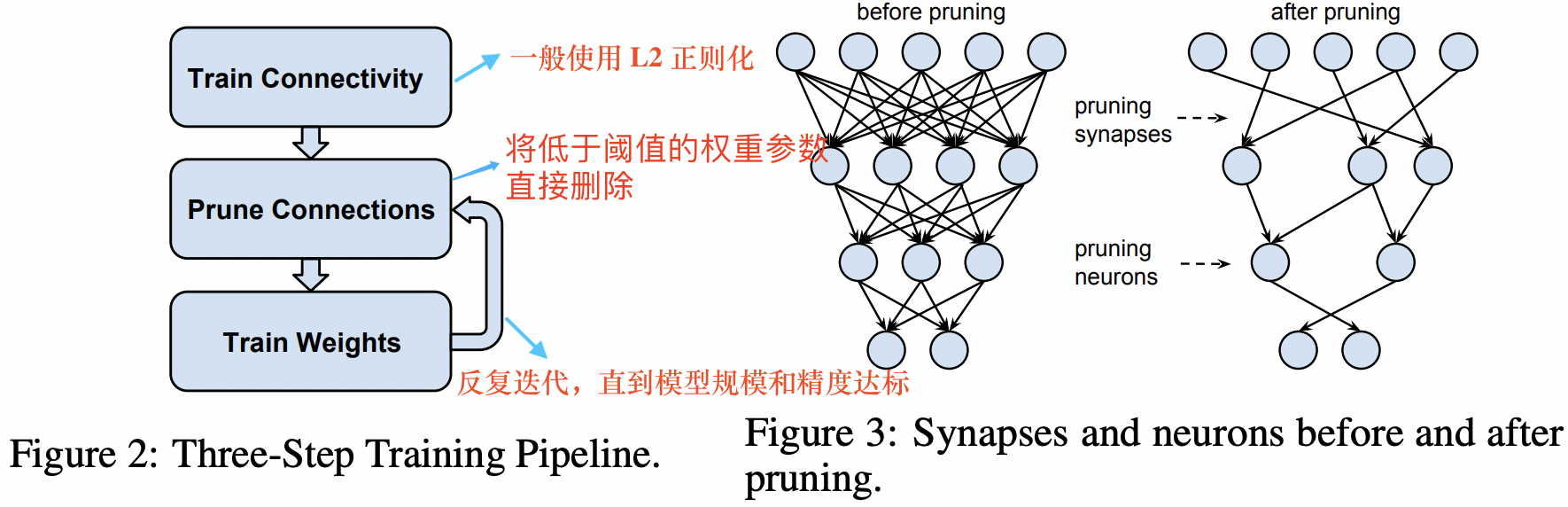
剪枝演演算法常用的迭代計算流程:訓練、剪枝、微調。

剪枝Three-Step Training Pipeline 中三個階段權重數值分佈如下圖所示。微調之後的模型權重分佈將部分地恢復正太分佈的特性。

深度網路中存在權重稀疏性:（a）剪枝前的權重分佈；（b）剪除0值附近權值後的權重分佈；（c）網路微調後的權重分佈

2.2，啟用稀疏

早期的神經網路模型-早期的神經網路模型——多層感知機（MLP）中，多采用Sigmoid函數作為啟用單元。但是其複雜的計算公式會導致模型訓練過慢，且隨著網路層數的加深，Sigmoid 函數引起的梯度消失和梯度爆炸問題嚴重影響了反向傳播演演算法的實用性。為解決上述問題，Hinton 等人於 2010 年在論文中[2]提出了 ReLU 啟用函數，並在 AlexNet模型[3]中第一次得到了實踐。

後續伴隨著 BN 層運算元的提出，「2D折積-BN層-ReLU啟用函數」三個運算元串聯而成的基本單元就構成了後來 CNN 模型的基礎元件，如下述 Pytorch 程式碼片段所示：

早期是「2D折積-ReLU啟用函數-池化」這樣串接的元件。

# cbr 元件範例程式碼
def convbn_relu(in_planes, out_planes, kernel_size, stride, pad, dilation):
    return nn.Sequential(
        nn.Conv2d(in_planes, out_planes, 
                  kernel_size=kernel_size, stride=stride, 
                  padding=dilation if dilation > 1 else pad, 
                  dilation=dilation, bias=False),
        nn.BatchNorm2d(out_planes),
        nn.ReLU(inplace=True)
        )

ReLU 啟用函數的定義為：

\[ReLU(x) = max(0, x) \]

該函數使得負半軸的輸入都產生 0 值的輸出，這可以認為啟用函數給網路帶了另一種型別的稀疏性；另外 max_pooling 池化操作也會產生類似稀疏的效果。即無論網路接收到什麼輸入，大型網路中很大一部分神經元的輸出大多為零。啟用和池化稀疏效果如下圖所示。

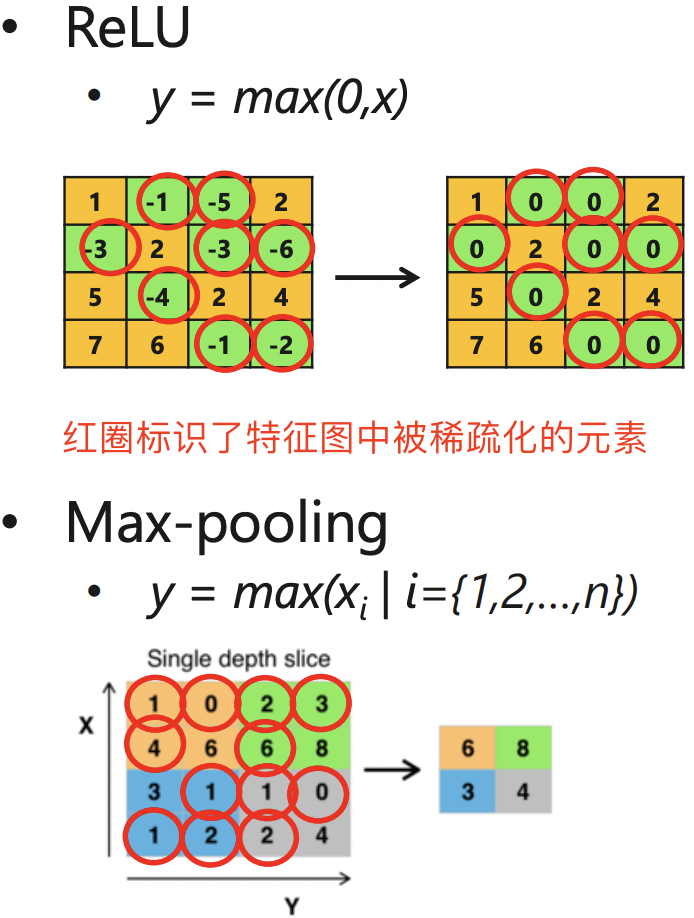
即 ReLU 啟用層和池化層輸出特徵圖矩陣是稀疏的。

受以上現象啟發，論文[4]經過了一些簡單的統計，發現無論輸入什麼樣影象資料，CNN 中的許多神經元都具有非常低的啟用。作者認為零神經元很可能是冗餘的（redundant），可以在不影響網路整體精度的情況下將其移除。因為它們的存在只會增加過度擬合的機會和優化難度，這兩者都對網路有害。

由於神經網路具有乘法-加法-啟用計算過程，因此其輸出大部分為零的神經元對後續層的輸出以及最終結果的貢獻很小。

由此，提出了一種神經元剪枝演演算法。首先，定義了 APoZ （Average Percentage of Zeros）指標來衡量經過 ReLU 對映後神經元零啟用的百分比。假設 \(O_c^{(i)}\)表示網路第 \(i\) 層中第 \(c\) 個通道（特徵圖），那麼第 \(i\) 層中第 \(c\) 個的濾波器（論文中用神經元 neuron）的 APoZ 定義如下:

\[APoZ^{(i)}_c = APoZ(O_c^{(i)}) = \frac{\sum_k^N \sum_j^M f(O^{(i)}_{c,j}(k=0))}{N \times M} \]

這裡，\(f\left( \cdot \right)\) 對真的表示式輸出 1，反之輸出 0，\(M\) 表示 \(O_c^{(i)}\) 輸出特徵圖的大小，\(N\) 表示用於驗證的影象樣本個數。由於每個特徵圖均來自一個濾波器（神經元）的折積及啟用對映結果，因此上式衡量了每個神經元的重要性。

下圖給出了在 VGG-16 網路中，利用 50,000 張 ImageNet 影象樣本計算得到的 CONV5-3 層的 512 個和 FC6 層的 4096 個 APoZ 指標分佈圖。

這裡更高是指更接近於模型輸出側的網路層。

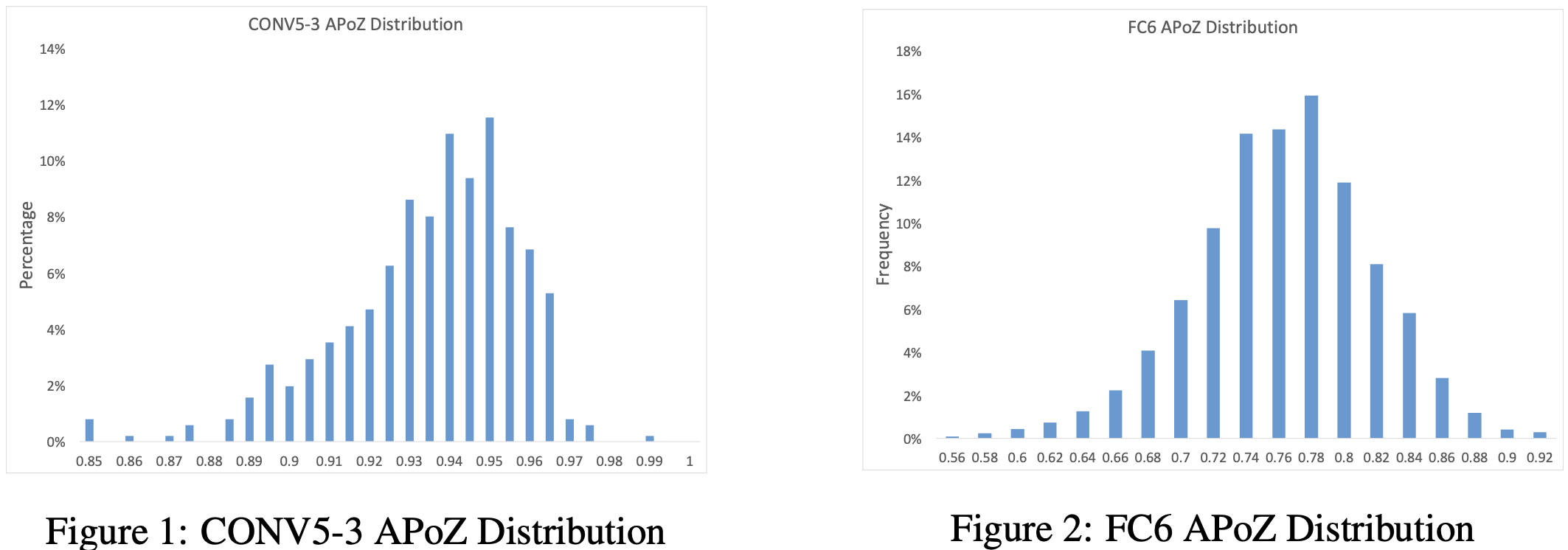
可以看出 CONV5-3 層的大多數神經元的該項指標都分佈在 93%附近。實際上，VGG-16 模型中共有 631 個神經元的 APoZ 值超過90%。啟用函數的引入反映出 VGG 網路存在著大量的稀疏與冗餘性，且大部分冗餘都發生在更高的折積層和全連線層。

啟用稀疏的工作流程和稀疏前後網路連線變化如下圖所示。

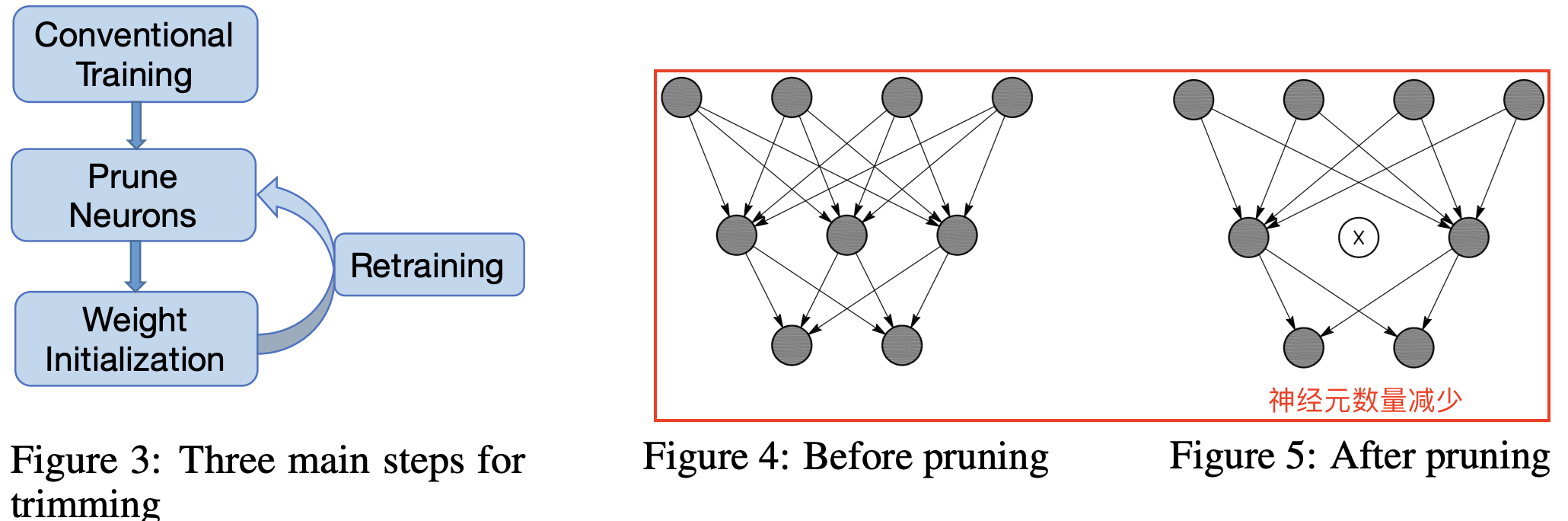
工作流程沿用韓鬆論文[1]提出的 Three-Step Training Pipeline，演演算法步驟如下所示:

首先，網路在常規過程下進行訓練，每層中的神經元數量根據經驗設定。接下來，我們在大型驗證資料集上執行網路以獲得每個神經元的 APoZ。
根據特定標準修剪具有高 APoZ 的神經元。當一個神經元被修剪時，與神經元的連線被相應地移除（參見上圖右邊紅色框）。
神經元修剪後，修剪後的網路使用修剪前的權重進行初始化。修剪後的網路表現出一定程度的效能下降。因此，在最後一步中，我們重新訓練網路以加強剩餘的神經元以增強修剪後網路的效能。

總結：和權重剪枝的代表作[1]隨機權重剪枝方法（神經元和連線都剪枝）相比，啟用剪枝的代表作[4]，其剪枝的直接物件是神經元（neuron），即隨機的將一些神經元的輸出置零，屬於結構化稀疏。

2.3，梯度稀疏

大模型（如BERT）由於引數量龐大，單臺主機難以滿足其訓練時的計算資源需求，往往需要藉助分散式訓練的方式在多臺節點（Worker）上共同作業完成。採用分散式隨機梯度下降（Distributed SGD）演演算法可以允許 \(N\) 臺節點共同完成梯度更新的後向傳播訓練任務。其中每臺主機均儲存一份完整的引數拷貝，並負責其中 \(\frac{1}{N}\) 引數的更新計算任務。按照一定時間間隔，節點在網路上釋出自身更新的梯度，並獲取其他 \(N-1\) 臺節點發布的梯度計算結果，從而更新原生的引數拷貝。

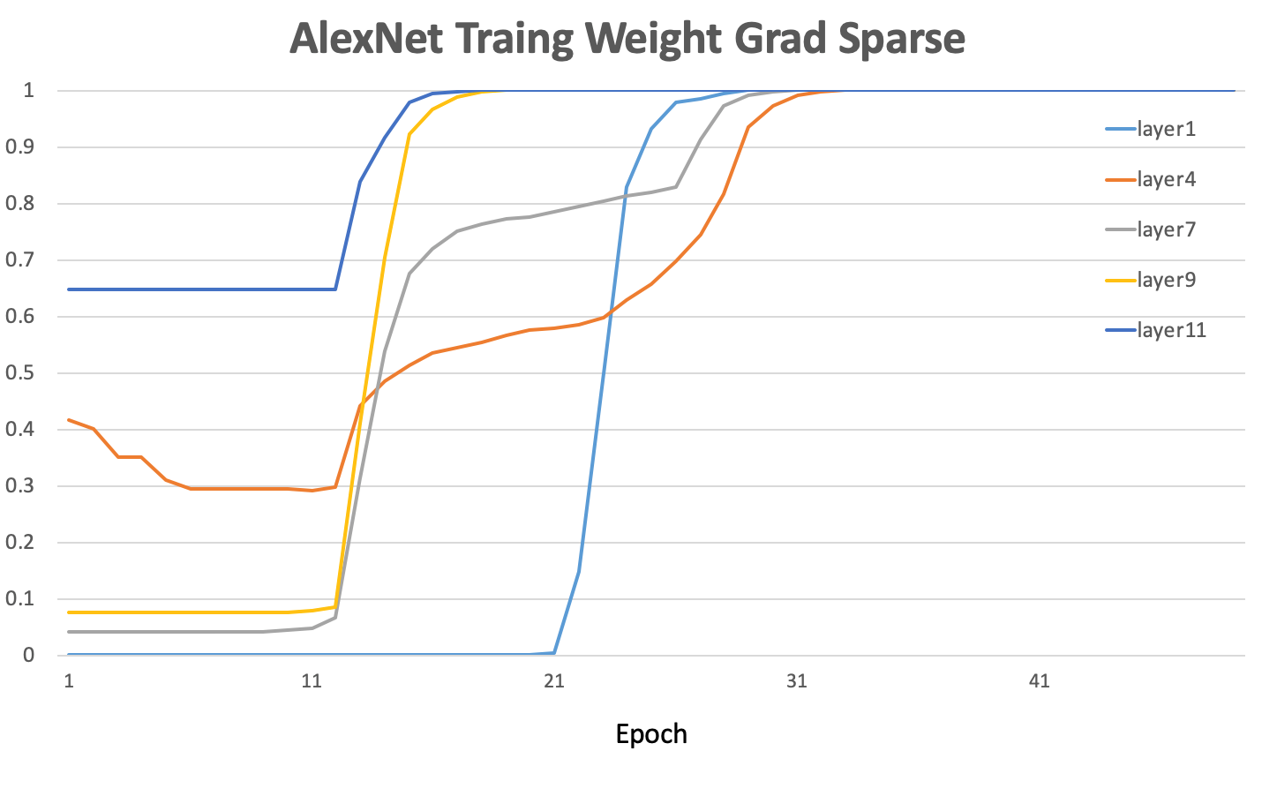
隨著參與訓練任務節點數目的增多，網路上傳輸的模型梯度資料量也急劇增加，網路通訊所佔據的資源開銷將逐漸超過梯度計算本身所消耗的資源，從而嚴重影響大規模分散式訓練的效率。另外，大多數深度神經網路模型引數的梯度其實也是高度稀疏的，有研究[5]表明在分散式 SGD 演演算法中，99.9% 的梯度交換都是冗餘的。例如下圖顯示了在 AlexNet 的訓練早期，各層引數梯度的幅值還是較高的。但隨著訓練週期的增加，引數梯度的稀疏度顯著增大。

AlexNet 模型的訓練是採用分散式訓練。深度神經網路訓練中的各層梯度值存在高度稀疏特性。

因為梯度交換成本很高，由此導致了網路頻寬成為了分散式訓練的瓶頸，為了克服分散式訓練中的通訊瓶頸，梯度稀疏（Gradient Sparsification）得到了廣泛的研究，其實現的途徑包括：

選擇固定比例的正負梯度更新：在網路上傳輸根據一定比例選出的一部分正、負梯度更新值。Dryden 等人2016年的論文。
預設閾值：在網路上僅僅傳輸那些絕對值幅度超過預設閾值的梯度。Heafield (2017)論文。

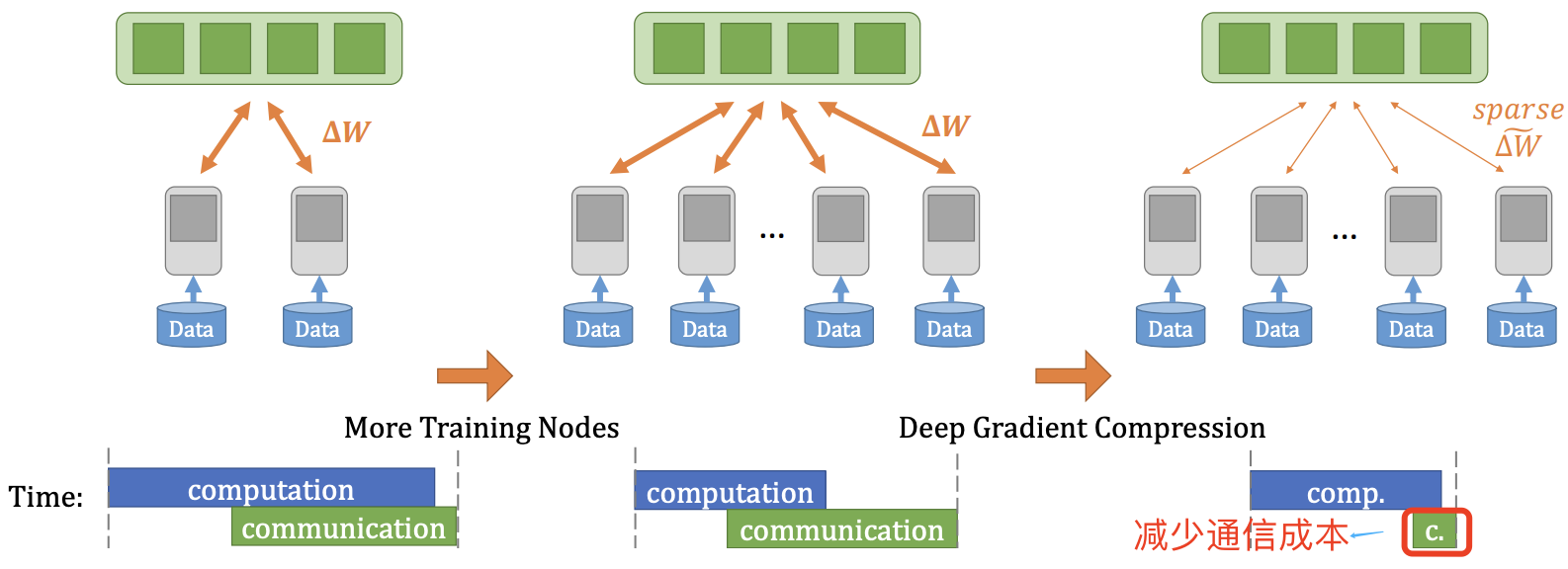
深度梯度壓縮（DGC）[5]，在梯度稀疏化基礎上採用動量修正、本地梯度剪裁、動量因子遮蔽和 warm-up訓練 4 種方法來做梯度壓縮，從而減少分散式訓練中的通訊頻寬。其演演算法效果如下圖所示。

2.4，小結

雖然神經網路稀疏化目前在學術界研究和工業界落地已經取得了寫進展，但是目前並沒有一個完全確定的知識體系框架，許多以前 paper 上的結論是可能被後續新論文打破和重建的。以下是對主流權重剪枝、啟用剪枝和梯度剪枝的總結:

早期的權重剪枝是非結構化的（細粒度稀疏）其對平行計算硬體-GPU支援並不友好，甚至可能完全沒有效果，其加速效果需要在專用加速器硬體（一般是 ASIC）上實現，比如韓鬆提出的 EIE 加速硬體[6]。
更高層的網路冗餘性更大，且折積層的冗餘性比全連線層的冗餘性更少。所以 ResNet、MobileNet 等網路的剪枝難度大於 VGG、AlexNet 等。
神經元剪枝相比權重剪枝更易損失模型精度，訓練階段的梯度則擁有最多的稀疏度。
典型的模型剪枝三段式工作 pipeline 流程並不一定是準確的，最新的研究表明，對於隨機初始化網路先進行剪枝操作再進行訓練，有可能會比剪枝預訓練網路獲得更高的稀疏度和精度。此需要更多研究。

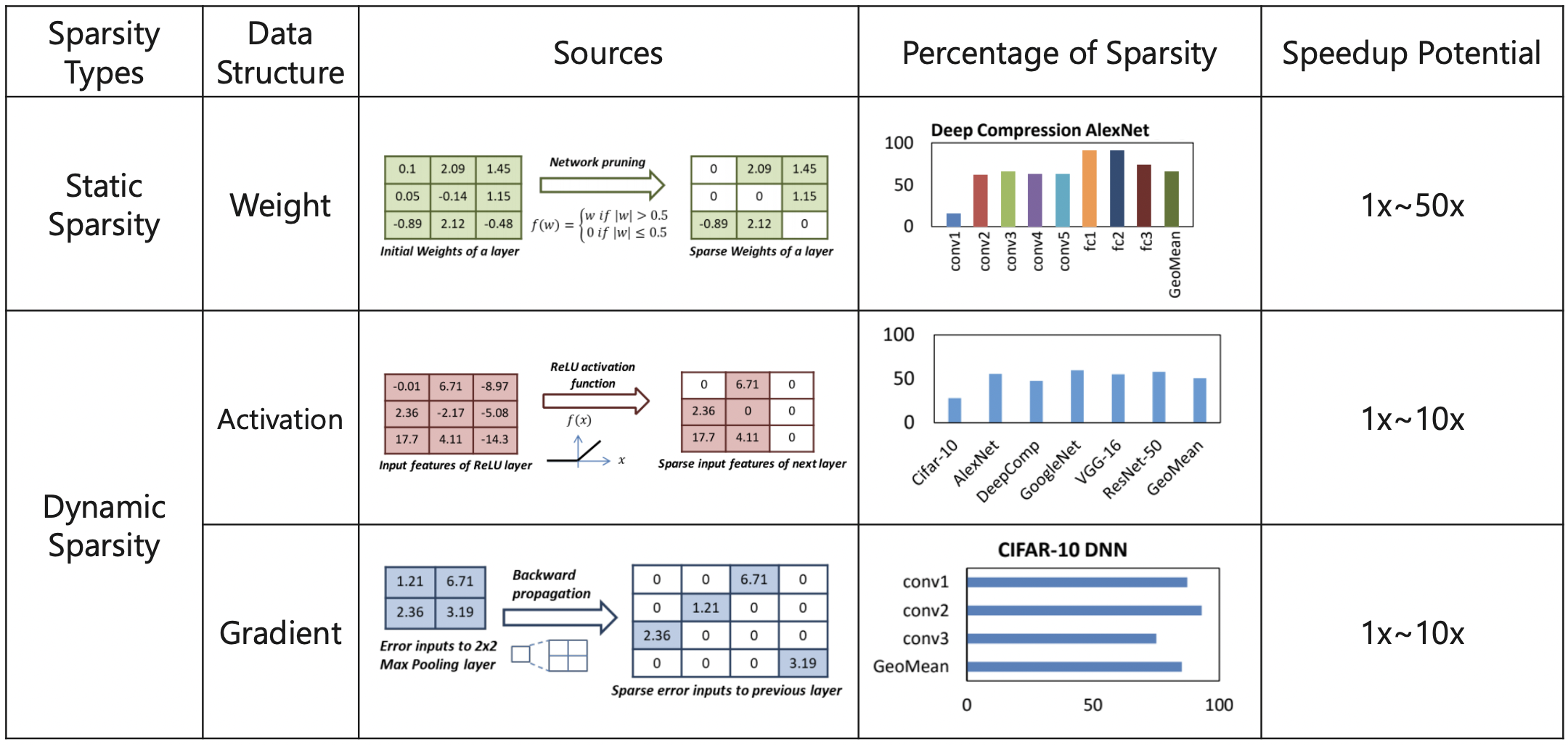
神經網路的稀疏性總結如下表所示:

三，結構化稀疏

早期提出的模型稀疏化[1][2]方法其實都是非結構化稀疏（即細粒度稀疏，也叫非結構化剪枝），其直接將模型大小壓縮10倍以上，理論上也可以減少10倍的計算量。但是，細粒度的剪枝帶來的計算特徵上的「不規則」，對計算裝置中的資料存取和大規模平行計算非常不友好，尤其是對 GPU硬體！

論文[1]作者提出了專用加速器硬體 EIE 去支援他的細粒度權重剪枝演演算法。

因為，「非結構化稀疏」（Unstructured Sparsity）主要通過對權重矩陣中的單個或整行、整列的權重值進行修剪。修剪後的新權重矩陣會變成稀疏矩陣（被修剪的值會設定為 0）。因而除非硬體平臺和計算庫能夠支援高效的稀疏矩陣計算，否則剪枝後的模型是無法獲得真正的效能提升的！

由此，許多研究開始探索通過給神經網路剪枝新增一個「規則」的約束-結構化剪枝（Structured pruning），使得剪枝後的稀疏模式更加適合並行硬體計算。「結構化剪枝」的基本修剪單元是濾波器或權重矩陣的一個或多個Channel。由於結構化剪枝沒有改變權重矩陣本身的稀疏程度，現有的計算平臺和框架都可以實現很好的支援。

這種引入了「規則」的結構化約束的稀疏模式通常被稱為結構化稀疏（Structured Sparsity），在很多文獻中也被稱之為粗粒度稀疏（Coarse-grained Sparsity）或塊稀疏（Block Sparsity）。

3.1，結構化稀疏分類

結構化剪枝又可進一步細分：可以是 channel-wise，也可以是 filter-wise，還可以是在shape-wise。

3.1.1，channel 剪枝

通道剪枝的工作是最多的，是最易於 IC 實現的。channel 剪枝和 filter 剪枝目前有些文章等同一個意思，有些區別開。

filter (channel) pruning (FP) 屬於粗粒度剪枝（或者結構化剪枝 Structured Pruning），基於 FP 的方法修剪的是過濾器或者折積層中的通道，而不是對個別權重，其原始的折積結構不改變，所以剪枝後的模型不需要專門的演演算法和硬體就能夠加速執行。

CNN 模型中通道剪枝的核心在於減少一箇中間特徵的數量，其前一個和後一個折積層需要發生相應的變化。論文Learning Efficient Convolutional Networks through Network Slimming[7] 認為 conv-layer 的每個channel 的重要程度可以和 bn 層關聯起來，如果某個 channel 後的 bn 層中對應的 scaling factor 足夠小，就說明該 channel 的重要程度低，可以被忽略。如下圖中橙色的兩個通道被剪枝。

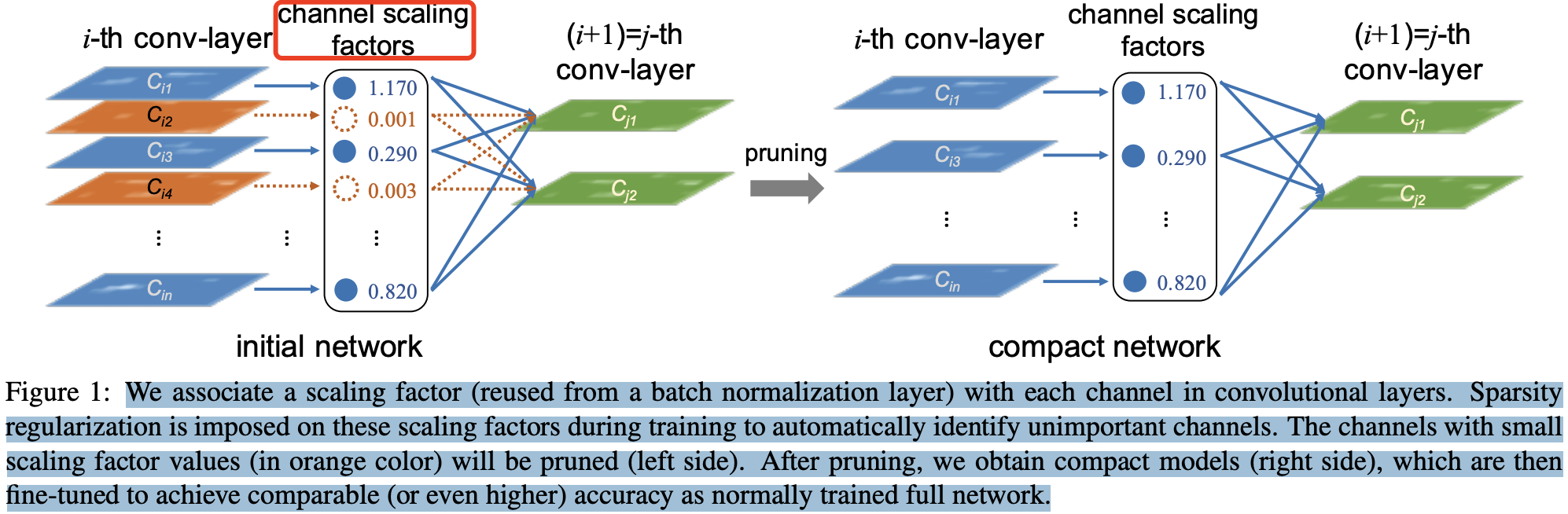
BN 層的計算公式如下：

\[\begin{aligned} \mu_B &= \frac{1}{m}\sum_1^m x_i \\ \sigma^2_B &= \frac{1}{m} \sum_1^m (x_i-\mu_B)^2 \\ n_i &= \frac{x_i-\mu_B}{\sqrt{\sigma^2_B + \epsilon}} \\ z_i &= \gamma n_i + \beta = \frac{\gamma}{\sqrt{\sigma^2_B + \epsilon}}x_i + (\beta - \frac{\gamma\mu_{B}}{\sqrt{\sigma^2_B + \epsilon}}) \end{aligned}\]

其中，bn 層中的 \(\gamma\) 引數被作為 channel-level 剪枝 所需的縮放因子（scaling factor）。

3.1.2，階段級別剪枝

濾波器級別的剪枝只能作用於殘差結構塊內部的折積層，CURL[9]中指出只進行濾波器級別的剪枝會導致模型形成一個沙漏狀、兩頭寬中間窄的結構，這樣的結構會影響引數量和計算量。在這種情況下，階段級別的剪枝能彌補濾波器級別剪枝的不足。

一個階段中的殘差結構塊是緊密聯絡在一起的，如下圖所示。

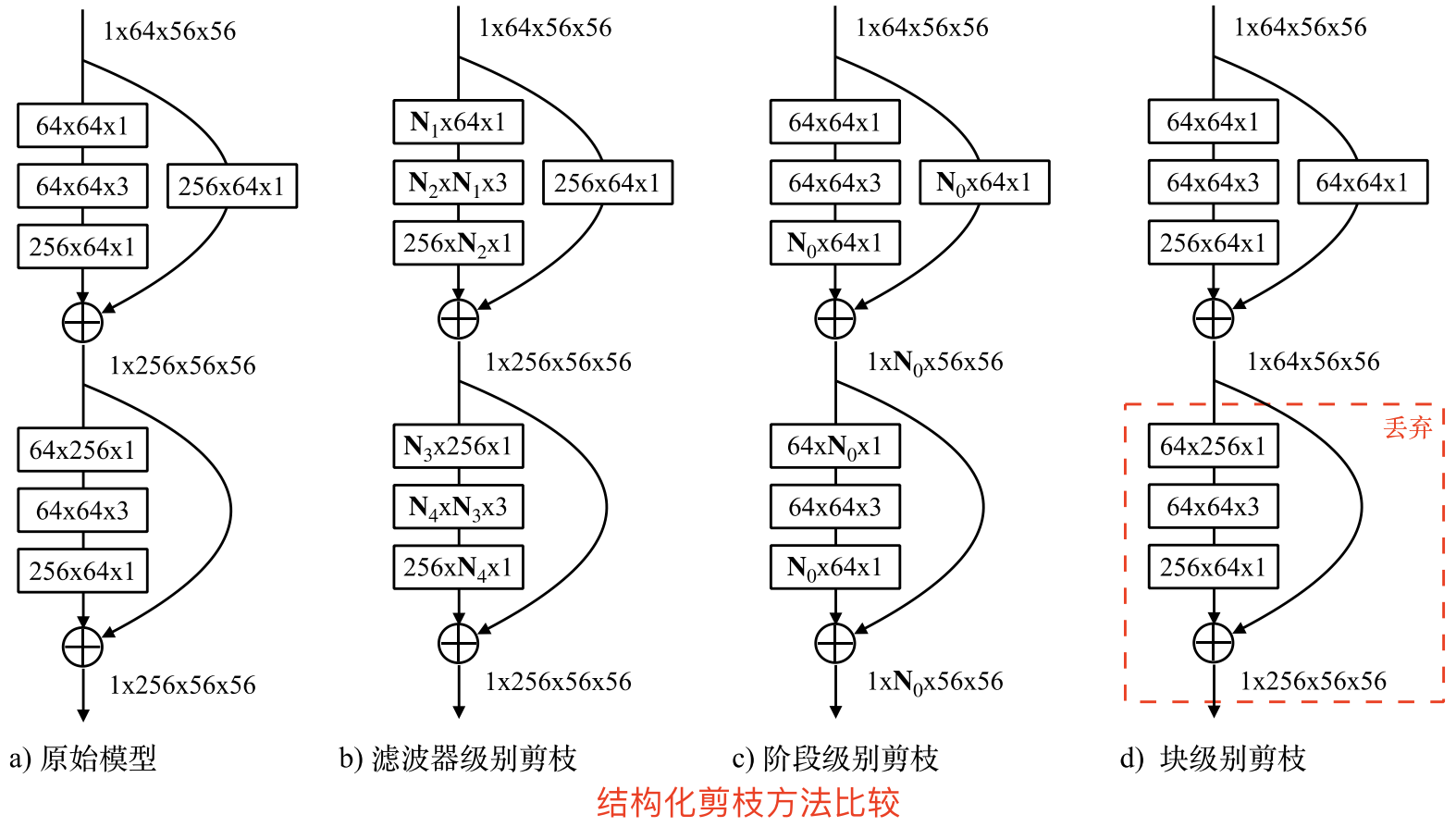
當一個階段的輸出特徵發生變化時（一些特徵被拋棄），其對應的每個殘差結構的輸入特徵和輸出特徵都要發生相應的變化，所以整個階段中，每個殘差結構的第一個折積層的輸入通道數，以及最後一個折積層的輸出通道數都要發生相同的變化。由於這樣的影響只限定在當前的階段，不會影響之前和之後的階段，因此我們稱這個剪枝過程為階段級別的剪枝（stage-level pruning）。

階段級別的剪枝加上濾波器級別的剪枝能夠使網路的形狀更均勻，而避免出現沙漏狀的網路結構。此外，階段級別的剪枝能夠剪除更多的網路引數，這給網路進一步壓縮提供了支援。

3.2，結構化稀疏與非結構化稀疏比較

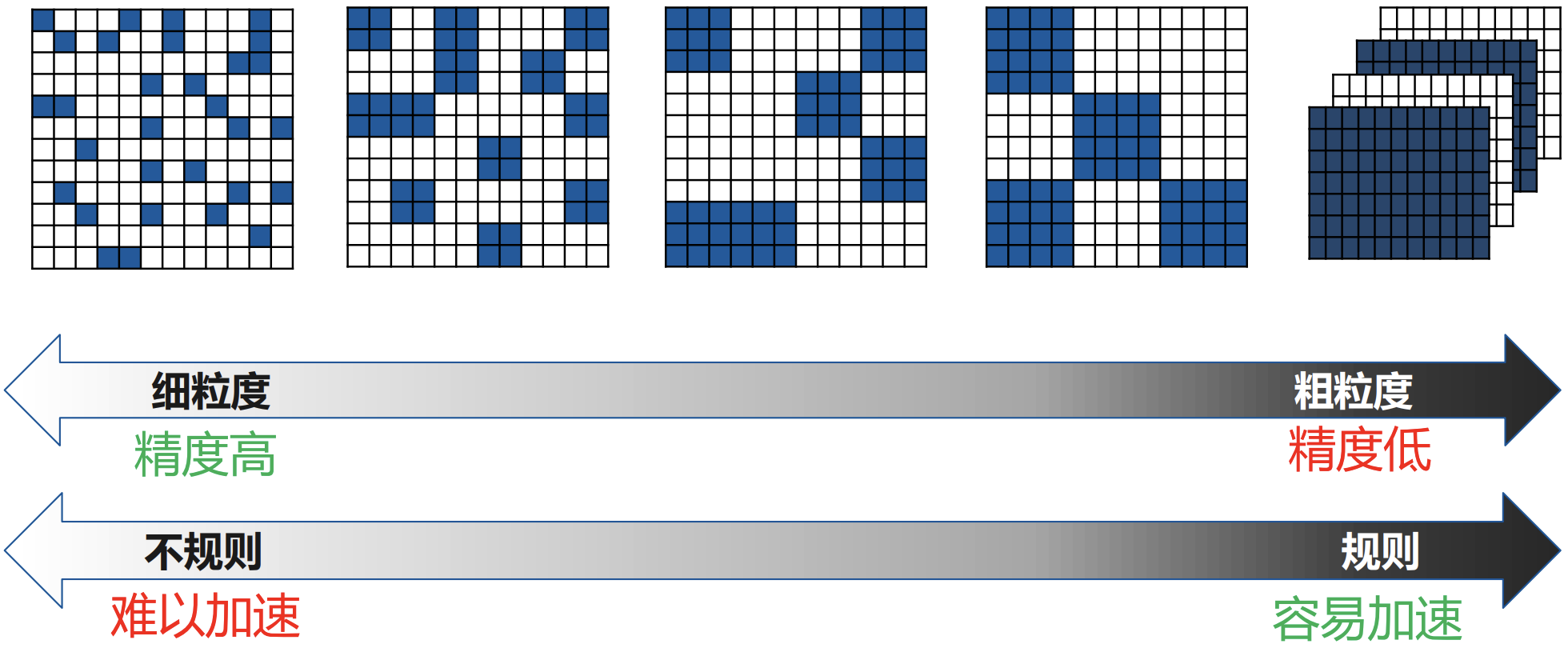
與非結構化剪枝相比，結構化剪枝通常通常會犧牲模型的準確率和壓縮比。結構化稀疏對非零權值的位置進行了限制，在剪枝過程中會將一些數值較大的權值剪枝，從而影響模型準確率。「非規則」的剪枝則契合了神經網路模型中不同大小權值的隨機分佈，這對深度學習模型的準確度至關重要。

深度神經網路的權值稀疏存在模型有效性和計算高效性之間的權衡。展開來講就是：

非結構化稀疏具有更高的模型壓縮率和準確性，但通用性不好。因為其計算特徵上的「不規則」，導致需要特定硬體支援才能實現加速效果。
結構化稀疏雖然犧牲了模型壓縮率或準確率，但通用性更好。因為結構化稀疏使得權值矩陣更規則更加結構化，更利於硬體加速。