圖折積神經網路分類的pytorch實現
圖神經網路(GNN)目前的主流實現方式就是節點之間的資訊匯聚,也就是類似於折積網路的鄰域加權和,比如圖折積網路(GCN)、圖注意力網路(GAT)等。下面根據GCN的實現原理使用Pytorch張量,和呼叫torch_geometric包,分別對Cora資料集進行節點分類實驗。
Cora是關於科學文獻之間參照關係的圖結構資料集。資料集包含一個圖,圖中包括2708篇文獻(節點)和10556個參照關係(邊)。其中每個節點都有一個1433維的特徵向量,即文獻內容的嵌入向量。文獻被分為七個類別:電腦科學、物理學等。
GCN計算流程
對於某個GCN層,假設輸入圖的節點特徵為$X\in R^{|V|\times F_{in}}$,邊索引表示為序號陣列$Ei\in R^{2\times |E|}$,GCN層輸出$Y\in R^{|V|\times F_{out}}$。計算流程如下:
0、根據$Ei$獲得鄰接矩陣$A_0\in R^{|V|\times |V|}$。
1、為了將節點自身資訊匯聚進去,每個節點新增指向自己的邊,即 $A=A_0+I$,其中$I$為單位矩陣。
2、計算度(出或入)矩陣 $D$,其中 $D_{ii}=\sum_j A_{ij}$ 表示第 $i$ 個節點的度數。$D$為對角陣。
3、計算對稱歸一化矩陣 $\hat{D}$,其中 $\hat{D}_{ii}=1/\sqrt{D_{ii}}$。
4、構建對稱歸一化鄰接矩陣 $\tilde{A}$,其中 $\tilde{A}= \hat{D} A \hat{D}$。
5、計算節點特徵向量的線性變換,即 $Y = \tilde{A} X W$,其中 $X$ 表示輸入的節點特徵向量,$W\in R^{F_{in}\times F_{out}}$ 為GCN層中待訓練的權重矩陣。
即:
$Y=D^{-0.5}(A_0+I)D^{-0.5}XW$
在torch_geometric包中,normalize引數控制是否使用度矩陣$D$歸一化;cached控制是否快取$D$,如果每次輸入都是相同結構的圖,則可以設定為True,即所謂轉導學習(transductive learning)。另外,可以看到GCN的實現只考慮了節點的特徵,沒有考慮邊的特徵,僅僅通過聚合引入邊的連線資訊。
GCN實驗
調包實現
Cora的圖資料存放在torch_geometric的Data類中。Data主要包含節點特徵$X\in R^{|V|\times F_v}$、邊索引$Ei\in R^{2\times |E|}$、邊特徵$Ea\in R^{|E|\times F_e}$等變數。首先匯出Cora資料:
from torch_geometric.datasets import Planetoid cora = Planetoid(root='./data', name='Cora')[0] print(cora)
構建GCN,訓練並測試。
import torch from torch import nn from torch_geometric.nn import GCNConv import torch.nn.functional as F from torch.optim import Adam class GCN(nn.Module): def __init__(self, in_channels, hidden_channels, class_n): super(GCN, self).__init__() self.conv1 = GCNConv(in_channels, hidden_channels) self.conv2 = GCNConv(hidden_channels, class_n) def forward(self, x, edge_index): x = torch.relu(self.conv1(x, edge_index)) x = torch.dropout(x, p=0.5, train=self.training) x = self.conv2(x, edge_index) return torch.log_softmax(x, dim=1) model = GCN(cora.num_features, 16, cora.y.unique().shape[0]).to('cuda') opt = Adam(model.parameters(), 0.01, weight_decay=5e-4) def train(its): model.train() for i in range(its): y = model(cora.x, cora.edge_index) loss = F.nll_loss(y[cora.train_mask], cora.y[cora.train_mask]) loss.backward() opt.step() opt.zero_grad() def test(): model.eval() y = model(cora.x, cora.edge_index) right_n = torch.argmax(y[cora.test_mask], 1) == cora.y[cora.test_mask] acc = right_n.sum()/cora.test_mask.sum() print("Acc: ", acc) for i in range(15): train(1) test()
僅15次迭代就收斂,測試精度如下:
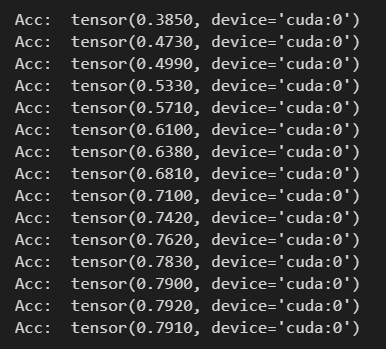
張量實現
主要區別就是自定義一個My_GCNConv來代替GCNConv,My_GCNConv定義如下:
from torch import nn from torch_geometric.utils import to_dense_adj class My_GCNConv(nn.Module): def __init__(self, in_channels, out_channels): super(My_GCNConv, self).__init__() self.weight = torch.nn.Parameter(nn.init.xavier_normal(torch.zeros(in_channels, out_channels))) self.bias = torch.nn.Parameter(torch.zeros([out_channels])) def forward(self, x, edge_index): adj = to_dense_adj(edge_index)[0] adj += torch.eye(x.shape[0]).to(adj) dgr = torch.diag(adj.sum(1)**-0.5) y = torch.matmul(dgr, adj) y = torch.matmul(y, dgr) y = torch.matmul(y, x) y = torch.matmul(y, self.weight) + self.bias return y
其它程式碼僅將GCNConv修改為My_GCNConv。
對比實驗
MLP實現
下面不使用節點之間的參照關係,僅使用節點特徵向量在MLP中進行實驗,來驗證GCN的有效性。
import torch from torch import nn import torch.nn.functional as F from torch.optim import Adam class MLP(nn.Module): def __init__(self, in_channels, hidden_channels, class_n): super(MLP, self).__init__() self.l1 = nn.Linear(in_channels, hidden_channels) self.l2 = nn.Linear(hidden_channels, hidden_channels) self.l3 = nn.Linear(hidden_channels, class_n) def forward(self, x): x = torch.relu(self.l1(x)) x = torch.relu(self.l2(x)) x = torch.dropout(x, p=0.5, train=self.training) x = self.l3(x) return torch.log_softmax(x, dim=1) model = MLP(cora.num_features, 512, cora.y.unique().shape[0]).to('cuda') opt = Adam(model.parameters(), 0.01, weight_decay=5e-4) def train(its): model.train() for i in range(its): y = model(cora.x[cora.train_mask]) loss = F.nll_loss(y, cora.y[cora.train_mask]) loss.backward() opt.step() opt.zero_grad() def test(): model.eval() y = model(cora.x[cora.test_mask]) right_n = torch.argmax(y, 1) == cora.y[cora.test_mask] acc = right_n.sum()/cora.test_mask.sum() print("Acc: ", acc) for i in range(15): train(30) test()
可以看出MLP包含了3層,並且隱層引數比GCN多得多。結果如下:
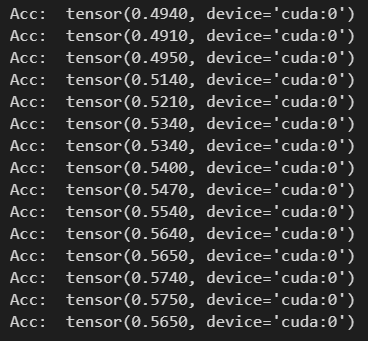
精度收斂在57%左右,效果比GCN的79%差。說明節點之間的連結關係對節點類別的劃分有促進作用,以及GCN的有效性。