關於這個「微信提現」的問題，太炸裂了，以至於我寫了段程式碼來驗證！

你好呀，我是歪歪。

週末的時候，我在網上看到一個關於微信錢包提現時，手續費收取的一個問題。

說真的，就這個問題吧，我個人覺得，放眼整個金融界，乃至於整個弱智吧，甚至於整個東半球，這都是一個相當炸裂的問題啊。

一時間，我居然恍惚了起來：一眼看去，漏洞百出。但是仔細分析之後，居然 TMD 無懈可擊？！

哎呀，這個問題，你就不能細琢磨，一琢磨，腦瓜仁就疼。

你知道的，我是一個行動派，所以我肯定得先驗證一波微信提現的手續費是否是這麼多。

於是我發起提現了，發現確實是有至少一角錢的手續費：

另外，我發現安卓的手機，在這個頁面中還無法截圖，所以我就只有通過拍照的方式搞到這個圖片了，所以看起來有點彆扭，你多擔待一下小老弟。

那麼第一個問題就來了：我提現一角，它手續費一角。請問我最終到手是多少錢呢？

0.1(元)-0.1(元)=0(元)，提現的錢全部扣了手續費，所以沒有錢到手。

對嗎？

邏輯上是合理的，但是如果微信真的敢這樣做的話，不就顯得很可（傻）愛（逼）嗎？

給你舉個例子：假設，我找你借了 100 元錢，然後我通過微信還給你的銀行卡（假設微信支援這個功能，類似於跨行轉賬），此時這筆轉賬對應的手續費是 1 元。如果從轉賬的金額裡面扣除，你收到的錢是 99 元。

你覺得這合理嗎？

如果你覺得合理的話，那麼請借給我 1w 吧，我應個急，十分鐘後就還你 9900 元。

什麼，你問我還有 100 元呢？

別問，問就是手續費，你找微信要去。

所以，正常的邏輯是從你的餘額裡面扣除。比如在我餘額還有 141.02 元的時候，我提取了一毛錢，那麼我的餘額變成了 140.82 元：

這裡，我還隱藏了一個邏輯。

比如你只提現一分錢的時候，如果你的微信餘額大於 0.1 元，那麼也是要收取 0.1 元的手續費的。

這句話，聽起來就想要流淚。

既然是從餘額中扣除，那麼當我餘額只有一毛錢的時候，我再次提現一毛錢，這個時候餘額不夠扣了，會出現什麼情況呢？

我也趕緊試了試：

140.82(元)-140.72(元)=0.1(元)

所以，我先給 Max 同學轉給了 140.72(元)：

此時我的微信錢包只剩下了 0.1 元：

這個時候，我再次提現 0.1 元的時候，發現微信居然告訴我：本次提現免費！！！

由此可得，當微信裡面剩下的錢不夠扣手續費的時候，本次提現就會免費。

這個免費，圈起來，後面要考。

實驗做完了，先把錢要回來再說：

啊！

大意了啊！

這樣一來，我這篇文章的成本就很高了啊。我居然一時間被實驗衝昏了頭腦，主動上交了私房錢？

但是我還有一個實驗場景沒有做啊？

就是當我微信錢包裡面的錢大於 0.1 元錢的時候，我點選「全部提現」會出現什麼場景呢？

於是我以做實驗的正當理由，成功的要回了一分錢：

這樣，我的餘額就變成了 0.11 元：

於是，當我點選「全部提現」的時候，雖然我已經預想到是這個場景了，但是我整個人還是沉默了，深深地沉默了。

我提現 0.11 元，手續費 0.1 元，到賬 0.01 元。

也就是說，當你全部提現，且提現的金額大於手續費，即 0.1 元的時候，微信的邏輯是從你提取的錢裡面扣除手續費。

也就是說我前面舉得轉賬的例子，是真的有可能出現轉出去，錢少了的情況。

麻繩專挑細處斷，厄運專找苦命人啊！

現在，我已經得到結論了，所以我不能再輸入密碼了，再輸入密碼，又得痛失一毛錢！

實驗現在已經結束了，結論我們也已經有了。

那麼，接下來，我們再看看最開始的，那個讓整個弱智吧，都為之「炸裂」的問題：

通過上面的實驗，我們得知，這個問題中的這句話「如果我每次都只取 0.1，然後它手續費收 0.1」是沒有任何問題的。

後半句：「就等於我一分錢都沒有拿到」。

這句話是值得商榷的，因為通過實驗證明，我最開始的時候，確實銀行卡到賬了 0.1 元。

但是，你要注意，我說「但是」了。

比如，我 1 元錢，每次提取 0.1 元，手續費 0.1 元，這樣 5 次之後我微信裡面的 1 元錢就變成了銀行卡 0.5 元和微信收取的手續費 0.5 元。

那麼，如果...

我是說如果，我把我銀行卡里面的 0.5 元再次充回到微信裡面，繼續重複上面的動作，事情是不是就開始變得有趣了？

所以，面試程式設計題就來了，請聽題：

已知，在微信錢包提現任意金額，都會收取至少 0.1 元的手續費，但是當餘額不足 0.1 元時除外。假設，小明現在有 100 元，他應該怎麼操作，才能把這 100 元錢，儘可能的全部變成手續費，白白送給微信？

請給我一段 Java 程式碼，入參是微信錢包裡面的餘額，紀錄檔列印出對應的操作過程。

拿到題，先不慌，分析一波。

首先，100 元，如果我每次只提取 0.1 元，收取 0.1 元手續費，那麼當我操作 500 次之後，我還有 50 元。500 次，剛好是微信餘額，100 元乘以 10，單位轉化為角之後，再除以 2。

再把 50 元，存回去分 250 次取出來。250 次，剛好是微信餘額，50 元乘以 10，單位轉化為角之後，再除以 2。

再把 25 元存回去分 125 次 取出來。125 次，剛好是微信餘額，25 元乘以 10，單位轉化為角之後，再除以 2。

再把 12.5 塊存回去分 62 次取出來，...

再把 6.2 存回去分 31 次取出來，...

迴圈往復，對吧。

也就說我每操作一次，我的微信餘額會少 0.2 元。

結合前面舉得例子，不難推理出來，我每一輪的操作次數，等於微信餘額乘以 10，單位轉化為角之後，再除以 2。

這個程式不難吧，起手就來：

public static void sbBehavior(double amount) {
    //應該還有 amount 小於 0 的邊界條件，節約篇幅，不寫了。
    if (amount <= 0.1) {
        //微信裡的錢不夠了扣手續費了,操作結束
        System.out.println("麻花藤:你只剩下:" + amount + "元了,謝謝老鐵~");
        return;
    }
    //金額擴大十倍,元轉角,好計算
    double totalJiao = amount * 10;
    //每一輪的操作次數，等於微信餘額除以 2
    int count = (int) (totalJiao / 2);
    //每一輪結束之後,共計手續費
    double fee = count * 0.1;
    //每一輪結束之後,銀行卡里剩下的錢
    double remainder = count * 0.1;
    System.out.println("微信錢包原金額 = " + amount + "元,操作次數=" + count + "次,手續費=" + fee + "元,剩餘金額=" + remainder + "元");
    //把銀行卡里剩下的錢充回微信,開始下一輪
    sbBehavior(remainder);
}

好，按照前面的思路，我寫出了這個程式，你就先看這個程式有什麼問題。我就明著告訴你，這個程式肯定是有問題的，你就去琢磨，到底有哪些問題。

來，我問你：誰教你金額計算用浮點型的？回去等通知吧。

當我們的入參為 100 的時候，上面那個程式跑完之後，你會發現結果是這樣的：

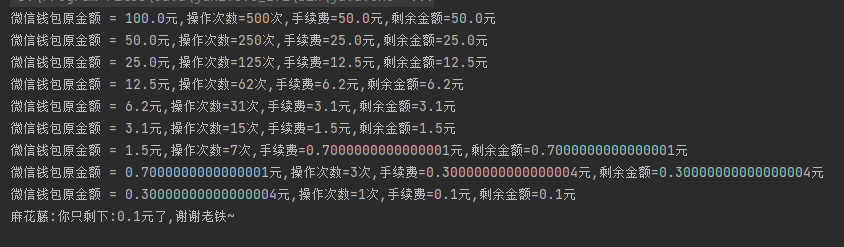
所以，牢記在心，只要涉及到金額的計算，一定一定一定要用 BigDecimal。而且我還附送你一條職場保命心經：用到 BigDecimal 時，具體保留多少小數位，具體的四捨五入規則，一定一定一定要讓需求提出方白紙黑字的寫在需求裡面，而不是你自己想當然的認為，保留兩位小數，採用四捨五入就行。後面出問題了，你啪的一下，就是把需求拿出來，你就不會很被動了。

回到我們的程式中，所以我們應該把程式修改成這樣：

public static void sbBehavior(BigDecimal amount) {
    if (amount.compareTo(new BigDecimal(0.1)) <= 0) {
        //微信裡的錢不夠了扣手續費了,操作結束
        System.out.println("麻花藤:你只剩下:" + amount + "元了,謝謝老鐵~");
        return;
    }
    //金額擴大十倍,元轉角,好計算
    BigDecimal jiao = amount.multiply(BigDecimal.TEN);
    //每一輪的操作次數，等於微信餘額除以 2
    BigDecimal count = jiao.divide(new BigDecimal(2), 0, RoundingMode.DOWN);
    //每一輪結束之後,共計手續費
    BigDecimal fee = count.multiply(new BigDecimal(0.1));
    //每一輪結束之後,銀行卡里剩下的錢
    BigDecimal remainder = count.multiply(new BigDecimal(0.1));
    System.out.println("微信錢包原金額 = " + amount + "元,操作次數=" + count + "次,手續費=" + fee + "元,剩餘金額=" + remainder + "元");
    //把銀行卡里剩下的錢充回微信,開始下一輪
    sbBehavior(remainder);
}

在上面的程式中，我把參與執行的地方全部都改成了 BigDecimal。但是這個程式還是有問題。

來，你繼續去琢磨，到底有哪些問題？

來，我問你：誰教你用 BigDecimal 參與計算的時候，用 new BigDecimal(0.1) 這個構造方法？

你用這個方法，idea 都會提醒你：老鐵，聽哥哥一句勸，還是用 String 型別的建構函式穩妥一點。

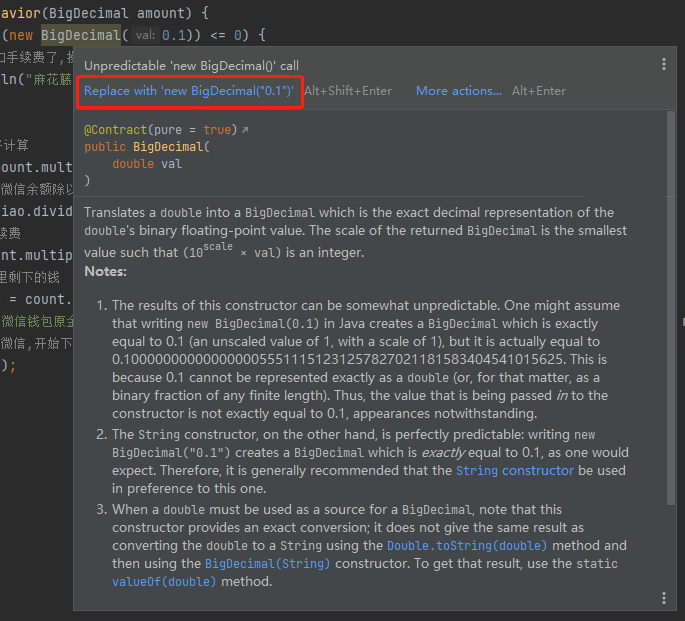
就上面這個程式，我給你跑一下，你就發現問題了，同樣還是有浮點數的問題：

所以，程式還得改一下，改成用 BigDecimal 的 String 型別的建構函式，其他啥都不動：

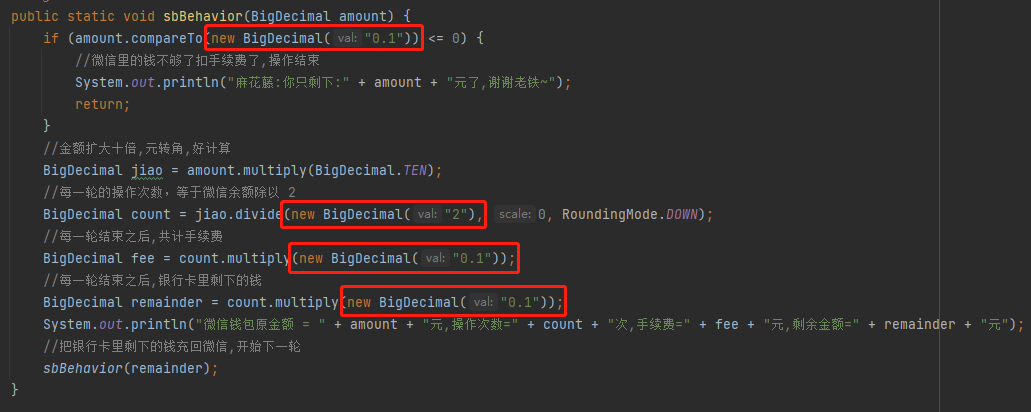
好，這個問題算是解決了。

你繼續說，這個程式還有啥問題？

如果你沒看出來的話，那麼我帶你看看輸出結果：

在這一次輸出的時候，手續費 6.2 元，剩餘金額 6.2 元，加起來才 12.4 元。但是我「微信錢包原金額」是 12.5 元啊？

還有一分錢去哪裡了呢？

所以我在一開始分析題的時候就給你下了一個套：

100 元，操作 500 次之後，還有 50 元。50 元，操作 250 次之後，還有 25 元。25 元，操作 150 次之後，還有 12.5 元...

如果你沒有帶著自己的思考看文章的話，那麼你可能就預設為操作一次之後，手續費和銀行卡的餘額都會增加 0.1 元。

也就是手續費和銀行卡的金額，和操作次數相關，所以寫出了這樣的程式碼：

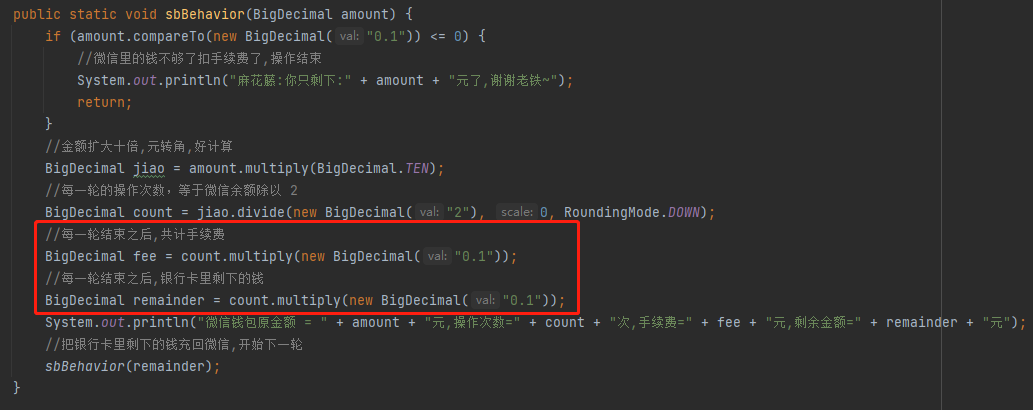
手續費，確實是每操作一次之後扣除 0.1 元，確實是和操作次數正相關。但是剩餘的錢，應該是用當前這一輪剩餘的總金額減去當前這一輪的總手續費。

也就是要把這一行程式碼修改為這樣：

拿著這個程式去跑的時候，你會發現輸出正常了，每一輪的金額加起來都能相等了：

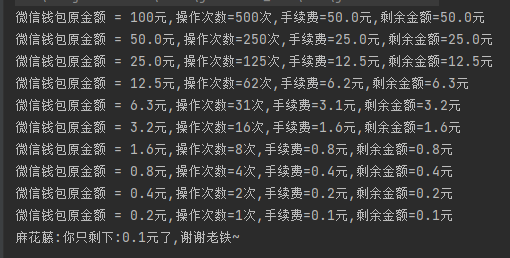
這下沒有任何毛病了。

那麼，注意，我現在要開始變形了。我要把題目變成：

請給我一段 Java 程式碼，入參是微信錢包裡面的餘額，出參是一共需要操作多少次。

在題目中，加了總操作次數的出參，我已經知道了每一輪操作的次數，算總次數這還不是手到擒來的事情？

分分鐘拿出程式碼：

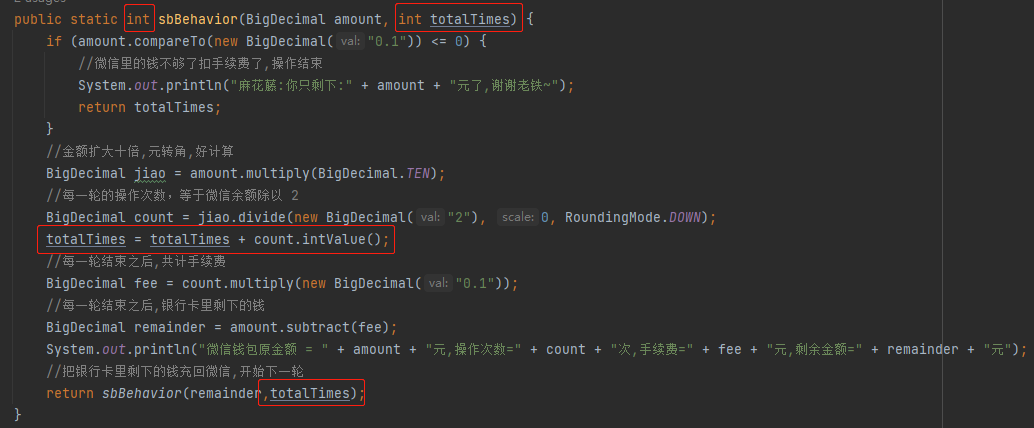
跑出結果：

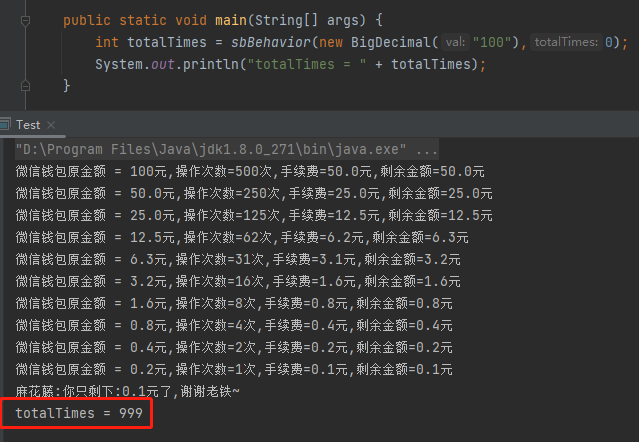
我們可以看到是 999 次。是的，不要質疑這個結果，當你有 100 元錢的時候，只需要操作 999 次，你就把自己的 99.9 元都給到微信了。

誒，朋友，你注意看，當我把金額變成 50 元的時候，總次數就是 499 了：

當我把金額變成 9.9 元的時候，總次數就變成了 98 次：

所以，請注意，我要「所以」了。

所以，如果我只要求操作的總次數，不要求輸出過程，那麼程式碼應該是怎麼樣的？

是不是把金額擴大十倍，變成角票，然後減去自己留下的一角錢，就是操作的總次數：

public static int sbBehavior(BigDecimal amount) {
    return amount.multiply(BigDecimal.TEN).subtract(BigDecimal.ONE).intValue();
}

這樣不就完事了嗎？

你忘記前面的所有內容，仔細的想想，是不是確實是這個道理？

假設你有 100 元，無論你怎麼操作，微信每次只會收 0.1 元的手續費，而你最多隻會剩下 0.1 元。

那麼你肯定得至少操作 999 次啊，這個小彎兒能轉過來吧？

好，轉過來了，是吧？

我再問你一個問題，假設我只有 0.19 元，我要把錢給微信，最多操作一次，然後我給它 0.1 元對吧？

但是，你用上面我給你的程式碼跑出來只會，輸出是 0：

是的，這個程式碼還是有問題的。

我就明確的告訴你，這個程式碼只適用於金額在 100.9 元到 0.19 元之間的數位。

至於為什麼，自己去琢磨。但是我不建議你去琢磨，因為這個玩意整個從最開始的地方就走偏了。

現在，請你忘記前面所有的程式碼，因為前面的程式碼，全都是錯的，我全程都在誤導你，讓你順著我的思路走。

其實你回想一下，最開始的時候，我為什麼要假設你微信裡面只有 100 元錢？

因為 100 元錢對應的手續費，不論你是提取一角錢，還是提取 100 元，100*0.001=0.1元，都剛好是 0.1 元。

然後我就開始告訴你，每次提現到銀行卡 0.1 元，手續費 0.1 元，巴拉巴拉巴拉~

但是，你有沒有想過，或者是看到哪個部分的時候，才恍然大悟：如果我有 1000 元呢？

如果我有 1000 元，那麼我第一次全部提現的話，手續費就是 1 元啊，而不是 0.1 元啊？

所以，你現在回過頭去看這行程式碼，是不是特別的搞笑：

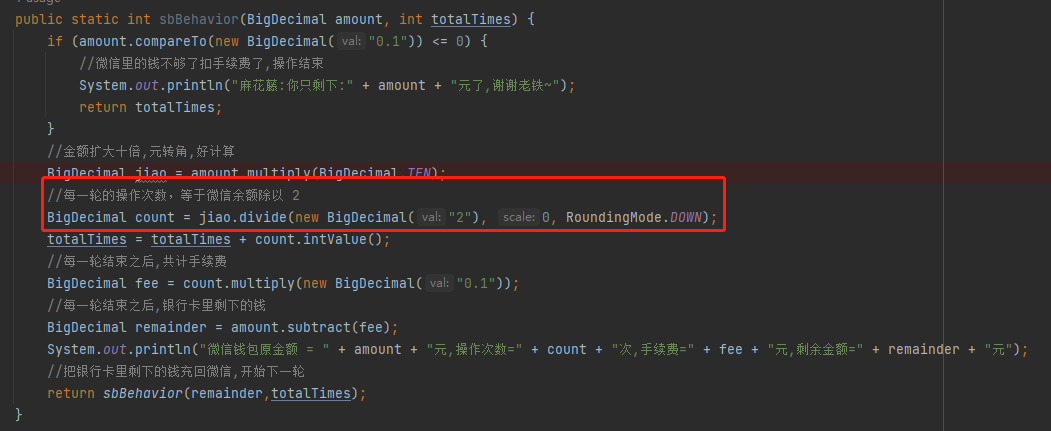
怎麼會去先計算次數，再根據次數反算其金額呢？

為了儘快的把錢都給到微信，肯定是每次儘量給到更多的手續費。已知手續費率是固定的，那麼提現的金額越高，手續費越高對吧？

所以，正確的操作應該是每次把微信錢包裡面的錢全部都取出來，也就是基於微信錢包裡面的錢，去計算手續費，計算剩餘的錢。

轉變了核心思路之後，程式碼就變成了這樣：

我也給你放一個粘過去就能用的程式碼：

public static int sbBehavior(BigDecimal amount, int totalTimes) {
    if (amount.compareTo(new BigDecimal("0.1")) <= 0) {
        //微信裡的錢不夠了扣手續費了,操作結束
        System.out.println("麻花藤:你只剩下:" + amount + "元了,謝謝老鐵~");
        return totalTimes;
    }
    //基於微信錢包裡面的錢，去計算手續費
    BigDecimal fee = amount.multiply(new BigDecimal("0.001")).setScale(2, BigDecimal.ROUND_UP);
    //手續費不足 0.1 元,則補齊為 0.1 元
    if (fee.compareTo(new BigDecimal("0.1")) <= 0) {
        fee = new BigDecimal("0.1");
    }
    //提現到銀行卡的錢
    BigDecimal remainder = amount.subtract(fee);
    totalTimes++;
    System.out.println("原現金 = " + amount + "元,操作=" + totalTimes + "次後,手續費=" + fee + "元,還剩下=" + remainder + "元");
    //把銀行卡里剩下的錢充回微信,開始下一輪
    return sbBehavior(remainder, totalTimes);
}

這樣，當我們有 1000 元的時候，每次做「全部提現」的動作，只需要操作 3257 次：

如果我們還是用之前一毛錢一毛錢的提法，得搞 9999 次。

效率提升 300%+。

舒服了！

而且這個是通用的邏輯，你就算給它 100 元，它也能給你算出是 999 次：

給它 0.19 元，它能給你算出是 1 次：

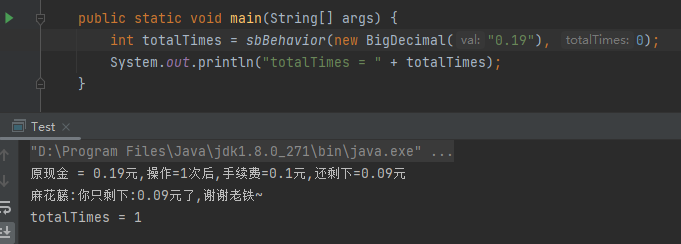
沒有任何毛病，但是，不知道你看到這裡，是否產生了一個疑問：為什麼我們要把錢儘可能的給微信呢？

那我給你換個角度：我們應該怎麼操作，才應該避免給微信手續費呢？

這樣一想，是不是思路就開啟了？

最後，如果這篇文章有那麼一個瞬間，讓你笑了一下的話，那麼，求個免費的「贊」，不過分吧？如果可以的話，關注一下我的公眾號「why技術」那就更好了，文章在公眾號全網首發