【動畫筆記】資料結構-AVL樹的插入操作

⚠ 本筆記前置知識: 二叉搜尋(排序)樹及其插入操作。

本文主要圍繞AVL樹的平衡因子、紙上做題思路、失衡型別(LL/RR/LR/RL)、失衡調整方法、插入後回溯這幾部分知識點展開。

• 注:

  1. 本筆記中的平衡二元樹規定所有左子樹都小於其父節點，所有右子樹都大於其父節點。

  2. 本筆記中的平衡因子計算方法是左子樹高度 - 右子樹高度。

目錄

• 簡單介紹一下下
  • 平衡因子
• 簡述平衡二元樹的插入操作
• 什麼是失衡節點
• 紙上快速做題思路
• 程式中定義樹節點
• 失衡型別 - LL型失衡
  • 舉例
  • 調整方法-右旋轉
  • 程式實現
• 失衡型別 - RR型失衡
  • 舉例
  • 調整方法-左旋轉
  • 程式實現
• 失衡型別 - LR型失衡
  • 舉例
  • 調整方法-先左旋轉再右旋轉
  • 程式實現
• 失衡型別 - RL型失衡
  • 舉例
  • 調整方法-先右旋轉再左旋轉
  • 程式實現
• 程式中判斷失衡型別
• 插入後一定要回溯到根節點嗎？
  • 遇到平衡因子為0的節點時回溯可以停止
  • 原因
• 相關題目
• 謝謝

簡單介紹一下下

AVL樹又稱二叉平衡搜尋(排序)樹，其最大的特點就是能維持所有節點的左右子樹高度差絕對值不大於1。

因此，AVL樹的插入操作要能維持住:

1. 二元搜尋樹的節點大小關係。

2. 平衡二元樹中每個節點的【平衡因子】絕對值不大於1。

平衡因子

一般對於AVL樹中的每個節點都會新增一個平衡因子(Balance Factor)欄位，平衡因子的值就是左右子樹的高度差，程式藉此判斷某棵子樹是否平衡。

簡述平衡二元樹的插入操作

AVL樹的插入操作在二叉搜尋(排序)樹的插入的基礎上新增瞭如下兩個過程:

1. 插入過程中將沿途比較的節點壓入棧。

2. 插入完成後，藉助彈棧來沿著插入時比較的各節點回到整棵樹的根節點 (從葉節點到根結點進行回溯):

   • 更新沿途各節點的高度。(通過高度計算平衡因子)

   • 沿途檢查各節點的平衡因子，若出現了平衡因子絕對值 > 1的情況，則對不平衡的子樹進行調整以保證整棵樹的平衡性。

✨ 當然，這裡的插入操作也是可以用遞回來實現的。

✨ 如果AVL樹節點中有指向父節點的指標變數，那麼這個過程就不需要棧輔助了，直接向上遍歷【插入節點】的所有祖先節點直至回到根節點即可。

什麼是失衡節點

當樹中某個節點的平衡因子 \(BF \notin \left [ -1,1 \right ]\) 時，這個節點就是失衡節點。

以這個失衡節點為根節點的子樹就是一棵不平衡的子樹。

紙上快速做題思路

這一招適合紙上解題，可以結合程式實現一起理解。
另外，字醜勿cue（╥﹏╥）

首先插入新節點（紅色的節點就是新插入的節點）:

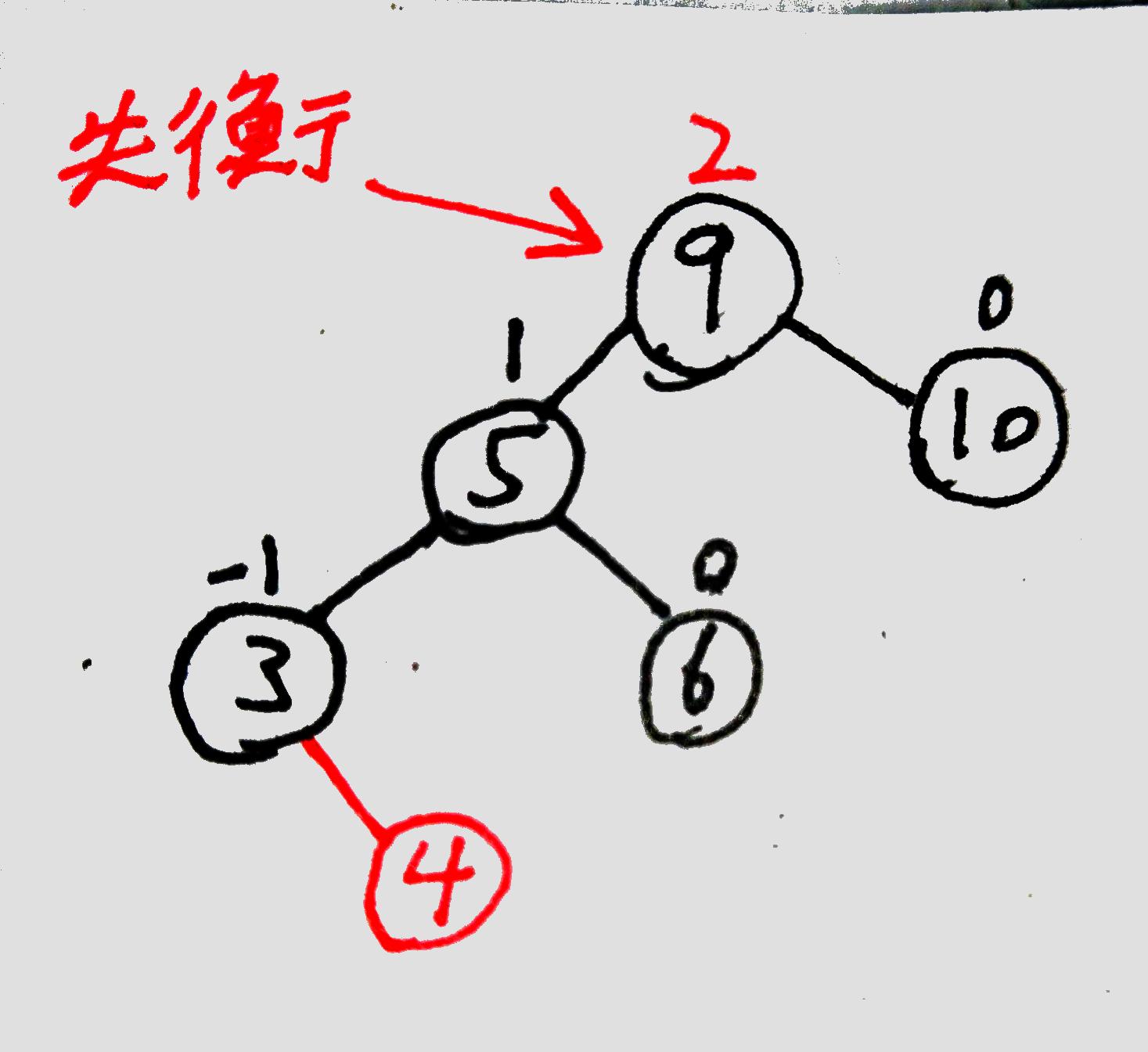
此時【值為9的節點】平衡因子為2，為失衡節點。

1. 從失衡節點開始，沿著【剛剛插入新節點的比較路徑】找，找到其中與其最鄰近的兩個點:

   

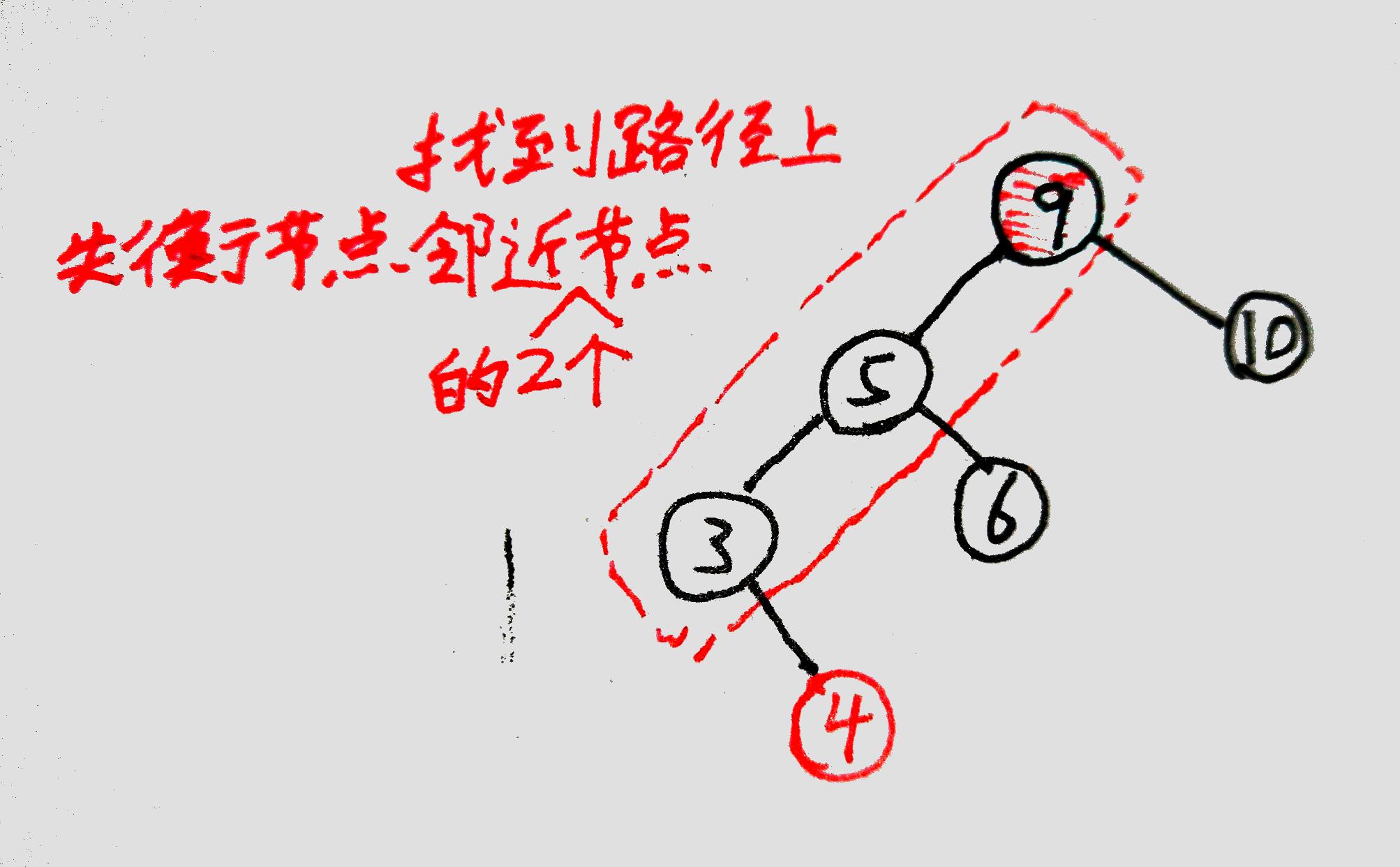
   （插入④時的比較路徑是⑨->⑤->③，因此圖中就找到了③、⑤、⑨）

2. 包括失衡節點在內，現在一共有三個節點，從中選擇值的大小在中間的節點。（圖中是⑤）

3. 將除了中間值節點外的兩個節點按照二元搜尋樹的規則接到【中間值節點】上，然後將【中間值節點】接到原本失衡節點所在的位置，作為這棵子樹的根節點。

   

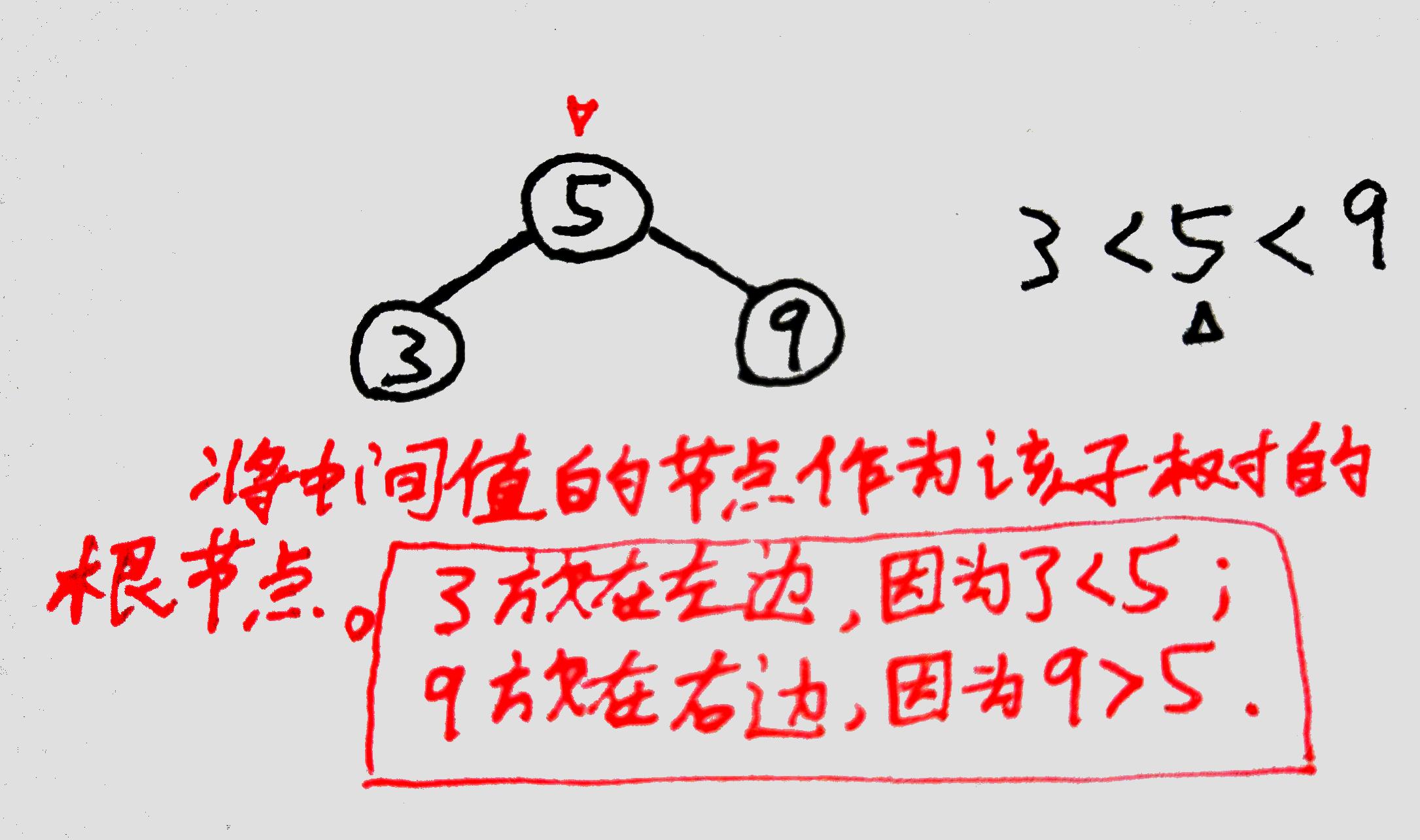
   （圖中⑤替換了原本⑨的位置，③和⑨變成了⑤的孩子）

4. 將【除了這三個節點之外】的節點按照二元搜尋樹插入規則插入到這三個節點組成的子樹中:

   

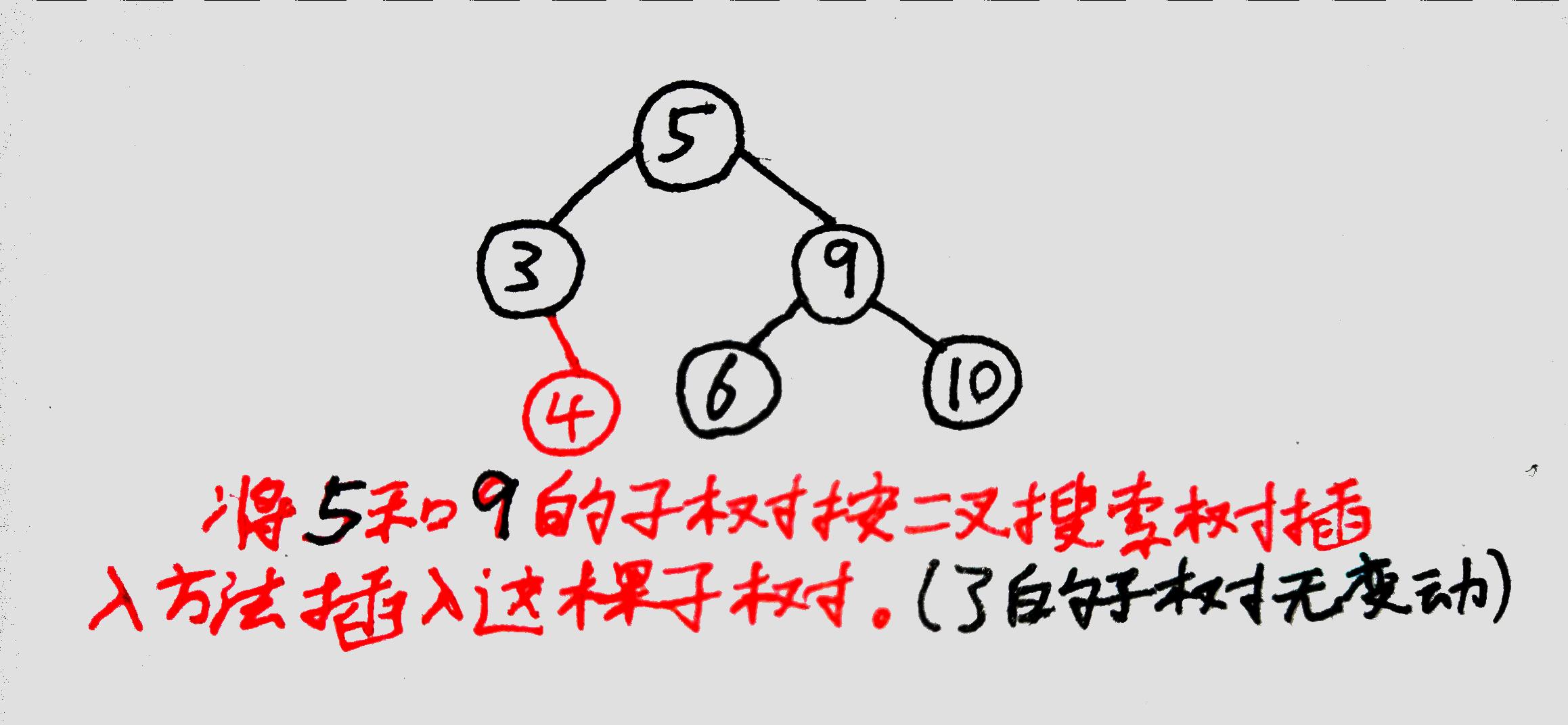
   （圖中就是把剩餘的節點④、⑥、⑩按規則插入到⑤為根的子樹中，實際上④沒有移動）

5. 更新各節點的平衡因子:

   

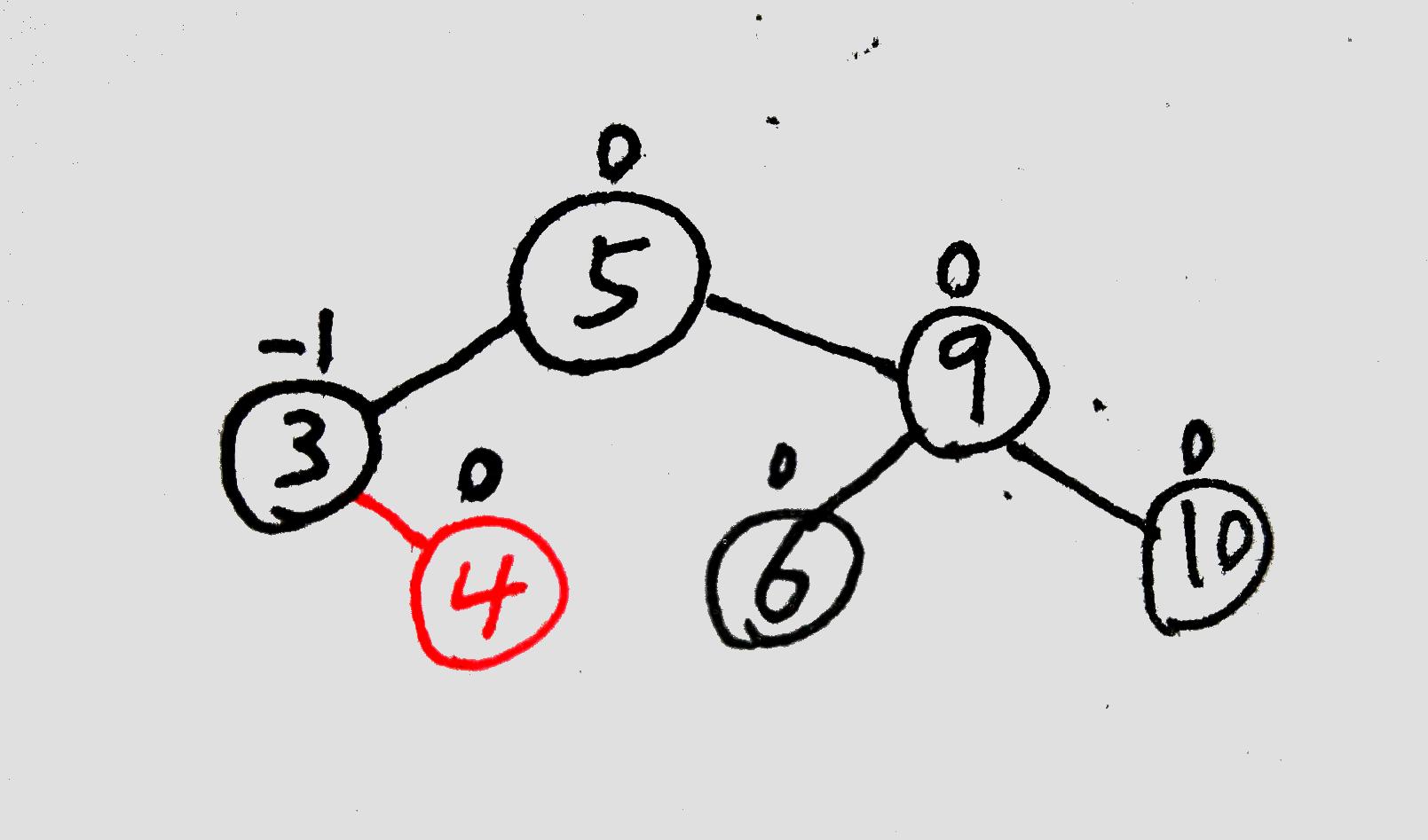
這種解題方法在紙上可以快速解決LL/LR/RL/RR這些型別的平衡調整問題，非常實用。

程式實現的話也可以靠這個思路來記憶和理解。

程式中定義樹節點

程式實現沒有標準答案，合理即可。

這裡的樹節點沒有指向父節點的指標，因此往樹中插入節點的過程中需要壓棧，以在插入完成後進行回溯。

typedef struct TreeNode *Tree;

struct TreeNode
{
    Tree left;  // 左子樹
    Tree right; // 右子樹
    int height; // 節點所在高度，平衡因子靠這個算
    int val;    // 節點值
};

失衡型別 - LL型失衡

LL型字面展開來看就是Left - Left。意思是新插入節點位於失衡節點的左孩子的左子樹中。

舉例

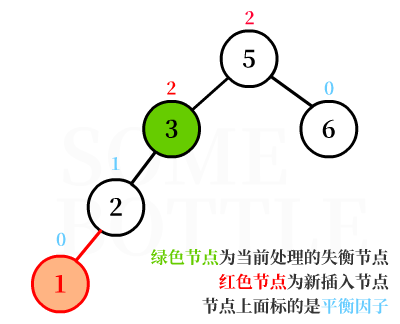
新節點插入在【值為2的節點】的左子樹中，而【值為2的節點】又是【值為3的節點】的左孩子。

此時【值為3的節點】的平衡因子BF = 2-0 = 2 > 1，是一個失衡節點。

• 注: 插入節點後的回溯過程當然是自下而上的，因此這裡指的是自下而上首個失衡節點。

可以發現新節點插在【失衡節點】的左孩子的左子樹中，這就是LL型失衡。

調整方法-右旋轉

這裡我結合紙上快速做題思路來寫一下。

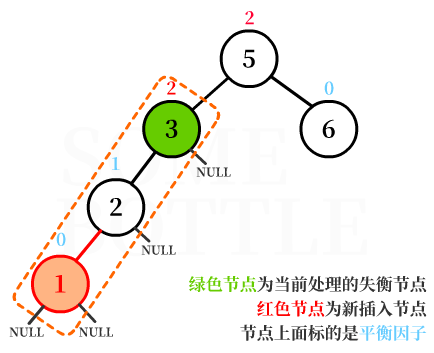
【值為3的節點】是失衡節點。

1. 找到失衡節點沿著插入路徑上的最鄰近的兩個節點，一共有三個節點。
   這裡可以看成是以失衡節點為根結點的子樹。

   • 就是圖中框出來的幾個節點。

2. 找到三個節點中【值在中間的節點】，接下來的「右旋轉」過程以它為軸。

   • 上圖中找出的就是【值為2的節點】。其實就是失衡節點的左孩子。

3. 將失衡節點以【值在中間的節點】為軸進行右旋轉(順時針)，讓【值在中間的節點】變成這棵子樹的新的根結點。

   • 上圖中的【值為3的節點】圍繞【值為2的節點】進行右旋轉，變成【值為2的節點】的右子樹。

   • 【值為2的節點】原本的右子樹變成【值為3的節點】的左子樹。

   • 【值為2的節點】成為新的子樹根結點。(詳見動圖)

• 動圖演示過程:

  

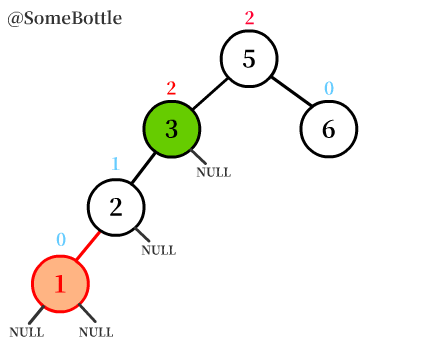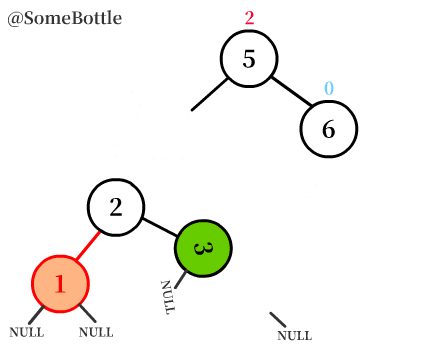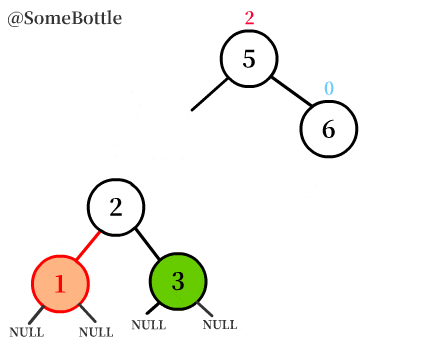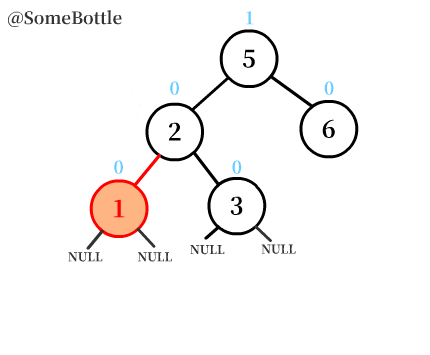
  通過動圖演示就能很直觀地看到這個「右旋轉」的過程。

  可以發現旋轉節點圍繞的「旋轉軸」就是【三個節點中中間值的節點】

  圖中我特意標出了空子樹NULL，程式實現的時候一定要把子樹考慮在內哦。

程式實現

程式實現的時候並不需要比較三個節點的大小。

對某個節點進行右旋轉操作時，實際上就是把這個節點繞著其左孩子進行順時針「旋轉」。

// 失衡節點右旋操作，node是失衡結點
void rotateRight(Tree node)
{
    Tree nodeLeft = node->left;         // 失衡節點左子樹
    Tree nodeRight = node->right;       // 失衡節點右子樹
    Tree lChildLeft = nodeLeft->left;   // 失衡節點的左孩子的左子樹
    Tree lChildRight = nodeLeft->right; // 失衡節點左孩子的右子樹
    // 這裡【沒有指向父節點】的指標，我們直接修改結點的值來模擬移動結點即可
    int nodeVal = node->val;   // 失衡節點的值
    node->val = nodeLeft->val; // 交換失衡節點和左孩子的值
    nodeLeft->val = nodeVal;
    // 這裡已經不是左孩子了，而是「旋轉」下來的失衡節點
    nodeLeft->left = lChildRight; // 修改結點的左右子樹
    nodeLeft->right = node->right;
    node->left = lChildLeft; // 和子樹的根結點接上
    node->right = nodeLeft;
    // 此時node是子樹根結點，lChildLeft是左子樹，nodeLeft是右子樹
    updateHeight(nodeLeft); // 更新有變動的結點的高度，先更新子樹再更新根
    updateHeight(node);
}

失衡型別 - RR型失衡

RR型字面展開來看就是Right - Right。意思是新插入節點位於失衡節點的右孩子的右子樹中。

舉例

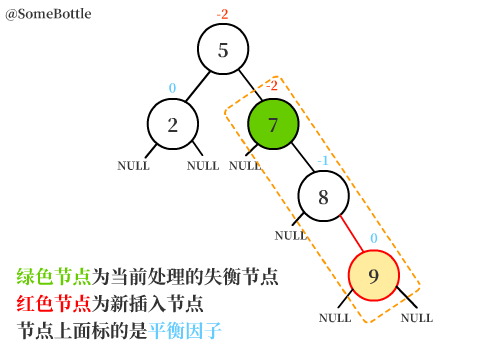
新節點插入在【值為8的節點】的右子樹中，而【值為8的節點】又是【值為7的節點】的右孩子。

此時【值為7的節點】的平衡因子BF = 0-2 = -2 < -1，是一個失衡節點。

可以發現新節點插在【失衡節點】的右孩子的右子樹中，這就是RR型失衡。

調整方法-左旋轉

【值為7的節點】是失衡節點。

1. 找到失衡節點沿著插入路徑上的最鄰近的兩個節點，一共有三個節點。
   這裡可以看成是以失衡節點為根結點的子樹。

   • 就是圖中框出來的幾個節點。

2. 找到三個節點中【值在中間的節點】，接下來的「左旋轉」過程以它為軸。

   • 上圖中找出的就是【值為8的節點】。其實就是失衡節點的右孩子。

3. 將失衡節點以【值在中間的節點】為軸進行左旋轉(逆時針)，讓【值在中間的節點】變成這棵子樹的新的根結點。

   • 上圖中的【值為7的節點】圍繞【值為8的節點】進行左旋轉，變成【值為8的節點】的左子樹。

   • 【值為8的節點】原本的左子樹變成【值為7的節點】的右子樹。

   • 【值為8的節點】成為新的子樹根結點。(詳見動圖)

• 動圖演示過程:

  

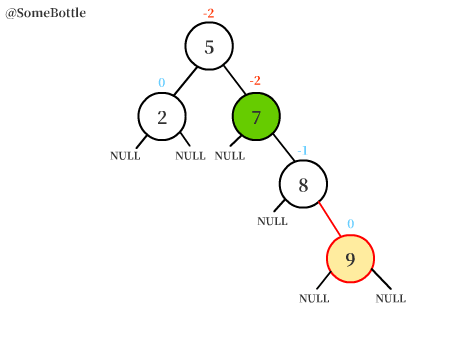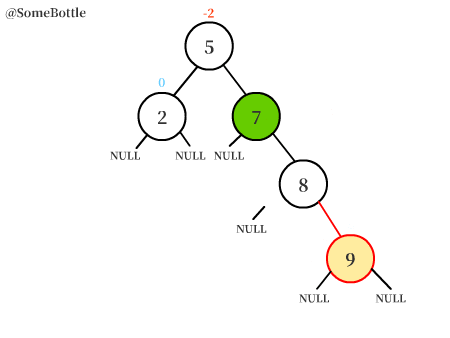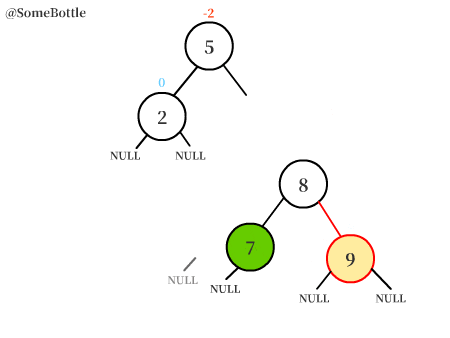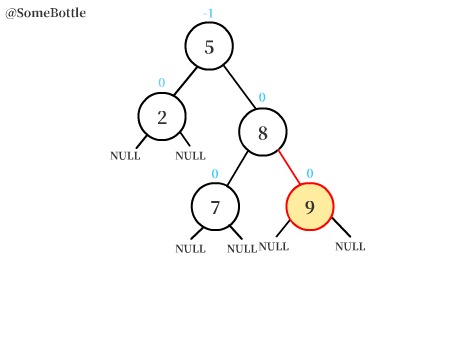
  RR型和LL型的調節過程中的操作是對稱的。

程式實現

程式實現的時候並不需要比較三個節點的大小。

對某個節點進行左旋轉操作時，實際上就是把這個節點繞著其右孩子進行逆時針「旋轉」。

// 失衡節點左旋操作，node是失衡節點
void rotateLeft(Tree node)
{
    Tree nodeLeft = node->left;          // 失衡節點左子樹
    Tree nodeRight = node->right;        // 失衡節點右子樹
    Tree rChildLeft = nodeRight->left;   // 失衡節點的右孩子的左子樹
    Tree rChildRight = nodeRight->right; // 失衡節點的右孩子的右子樹
    // 這裡【沒有指向父節點】的指標，我們直接修改結點的值來模擬移動結點
    int nodeVal = node->val;
    node->val = nodeRight->val; // 交換失衡節點和右孩子的值
    nodeRight->val = nodeVal;
    // 這裡的nodeRight就是「旋轉」下來的節點
    nodeRight->right = rChildLeft;
    nodeRight->left = node->left;
    node->left = nodeRight;
    node->right = rChildRight;
    // 此時node是子樹根結點，nodeRight是左子樹，rChildRight是右子樹
    updateHeight(nodeRight); // 更新有變動的結點的高度，先更新子樹再更新根
    updateHeight(node);
}

失衡型別 - LR型失衡

LR型字面展開來看就是Left - Right。意思是新插入節點位於失衡節點的左孩子的右子樹中。

舉例

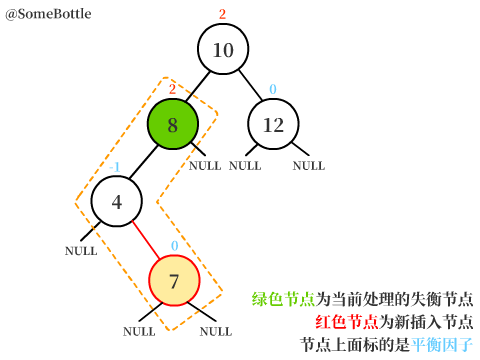
新節點插入在【值為4的節點】的右子樹中，而【值為4的節點】又是【值為8的節點】的左孩子。

此時【值為8的節點】的平衡因子BF = 2-0 = 2 > 1，是一個失衡節點。

可以發現新節點插在【失衡節點】的左孩子的右子樹中，這就是LR型失衡。

調整方法-先左旋轉再右旋轉

【值為8的節點】是失衡節點。

1. 找到失衡節點沿著插入路徑上的最鄰近的兩個節點，一共有三個節點。
   這裡可以看成是以失衡節點為根結點的子樹。

   • 就是圖中框出來的幾個節點。

2. 找到三個節點中【值在中間的節點】，接下來的「左旋轉」過程以它為軸。

   • 上圖中找出的就是【值為7的節點】。其實是失衡節點的左孩子的右孩子。

3. 將【(三個節點中)值最小的節點】以【值在中間的節點】為軸進行左旋轉(逆時針)，讓【值在中間的節點】轉上來，轉變成LL型失衡的情況。

   • 上圖中的【值為4的節點】圍繞【值為7的節點】進行左旋轉，變成【值為7的節點】的左子樹。

   • 【值為7的節點】原本的左子樹變成【值為4的節點】的右子樹。

   • 【值為7的節點】成為了【值為8的節點】的左孩子。

4. 此時整棵樹已經調整成了LL型失衡的情況，接著用右旋轉進行調整即可。詳見動圖。

• 動圖演示過程:

  

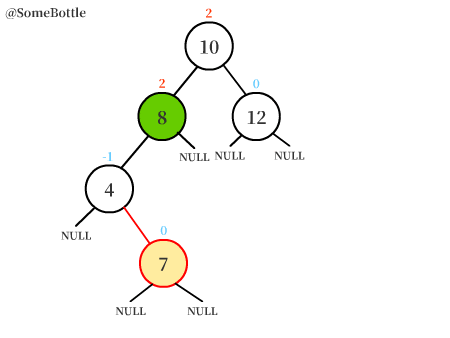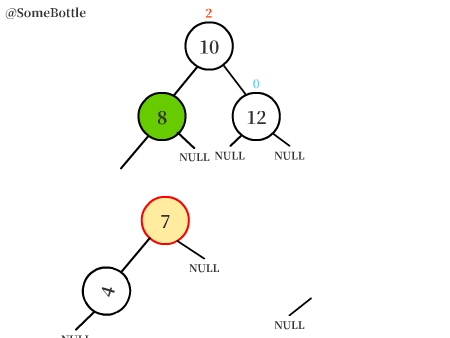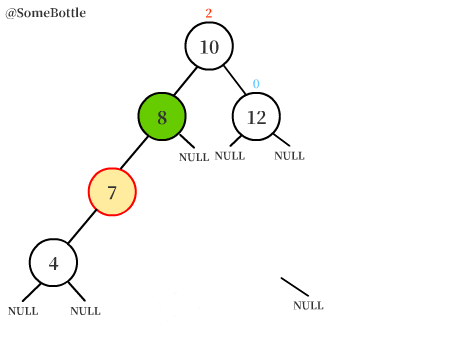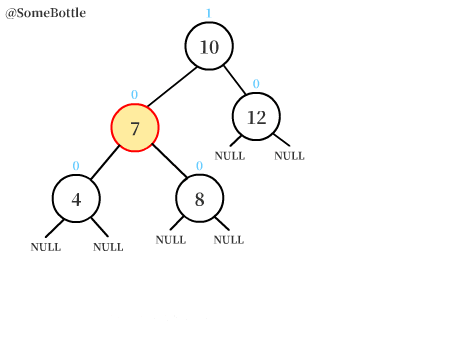
  可以很直觀地看到，首先用左旋轉將平衡樹轉變為了LL失衡的情況，再用右旋轉對樹進行調整。

  可以發現整個過程中，旋轉節點圍繞的「旋轉軸」都是【三個節點中中間值的節點】

程式實現

程式實現的時候並不需要比較三個節點的大小。

對某個節點A進行左旋轉+右旋轉操作時，實際上做的是:

1. 令該節點A的左孩子為B，首先將B繞著B的右孩子進行逆時針旋轉。
   (對B進行左旋轉)

2. 然後將節點A繞著B進行順時針旋轉。
   (對A進行右旋轉)

// 失衡節點左右旋操作，node是失衡節點
rotateLeft(node->left); // 先對失衡節點的左孩子進行左旋
rotateRight(node);      // 再對失衡節點進行右旋

失衡型別 - RL型失衡

RL型字面展開來看就是Right - Left。意思是新插入節點位於失衡節點的右孩子的左子樹中。

舉例

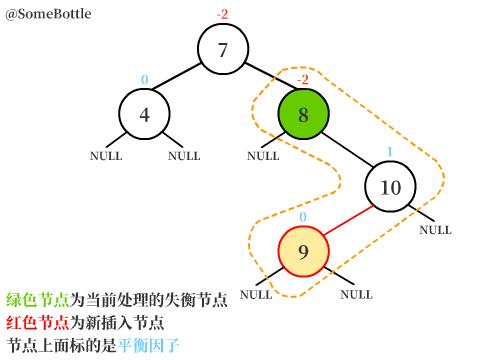
新節點插入在【值為10的節點】的左子樹中，而【值為10的節點】又是【值為8的節點】的右孩子。

此時【值為8的節點】的平衡因子BF = 0-2 = -2 < -1，是一個失衡節點。

可以發現新節點插在【失衡節點】的右孩子的左子樹中，這就是RL型失衡。

調整方法-先右旋轉再左旋轉

【值為8的節點】是失衡節點。

1. 找到失衡節點沿著插入路徑上的最鄰近的兩個節點，一共有三個節點。
   這裡可以看成是以失衡節點為根結點的子樹。

   • 就是圖中框出來的幾個節點。

2. 找到三個節點中【值在中間的節點】，接下來的「右旋轉」過程以它為軸。

   • 上圖中找出的就是【值為9的節點】。其實是失衡節點的右孩子的左孩子。

3. 將【(三個節點中)值最大的節點】以【值在中間的節點】為軸進行右旋轉(順時針)，讓【值在中間的節點】轉上來，轉變成RR型失衡的情況。

   • 上圖中的【值為10的節點】圍繞【值為9的節點】進行右旋轉，變成【值為9的節點】的右子樹。

   • 【值為9的節點】原本的右子樹變成【值為10的節點】的左子樹。

   • 【值為9的節點】成為了【值為8的節點】的右孩子。

4. 此時整棵樹已經調整成了RR型失衡的情況，接著用左旋轉進行調整即可。詳見動圖。

• 動圖演示過程:

  

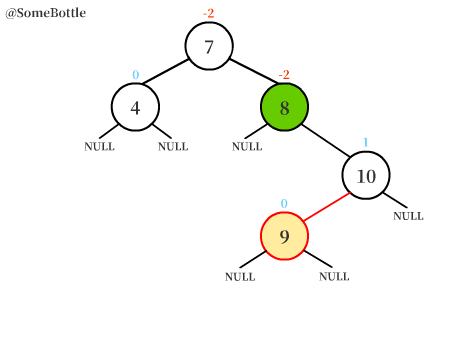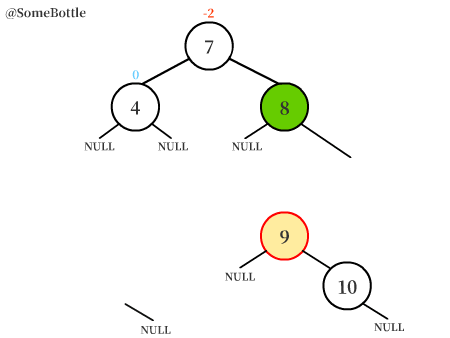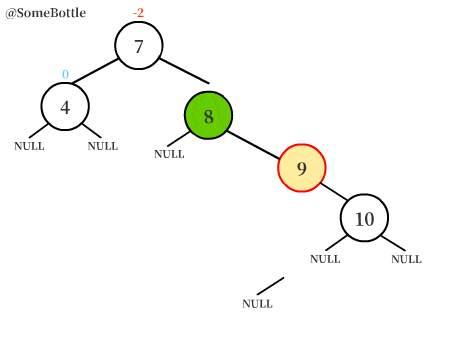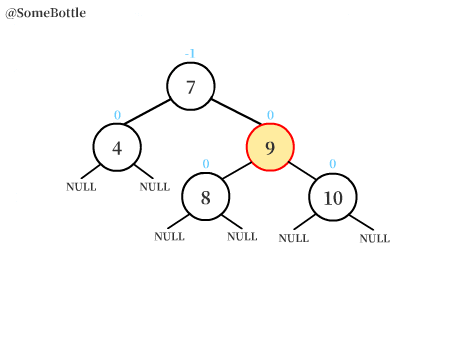
  可以很直觀地看到，首先用右旋轉將平衡樹轉變為了RR失衡的情況，再用左旋轉對樹進行調整。

  LR型和RL型的調節過程中的操作也是對稱的。

  可以發現整個過程中，旋轉節點圍繞的「旋轉軸」始終都是【三個節點中中間值的節點】

程式實現

程式實現的時候並不需要比較三個節點的大小。

對某個節點A進行右旋轉+左旋轉操作時，實際上做的是:

1. 令該節點A的右孩子為B，首先將B繞著B的左孩子進行順時針旋轉。
   (對B進行右旋轉)

2. 然後將節點A繞著B進行逆時針旋轉。
   (對A進行左旋轉)

// 失衡節點右左旋操作，node是失衡節點
rotateRight(node->right); // 先對失衡節點的右孩子進行右旋
rotateLeft(node);         // 再對失衡節點進行左旋

程式中判斷失衡型別

程式中，咱們依賴於平衡因子來判斷失衡型別。

平衡因子由左右子樹的高度差決定，因此根據平衡因子能判斷出新節點插入在哪裡:

• 當失衡節點的平衡因子 > 1 時:

  • 如果失衡節點的左孩子的平衡因子 > 0，則是LL型失衡。

  • 如果失衡節點的左孩子的平衡因子 < 0，則是LR型失衡。

• 當失衡節點的平衡因子 < -1 時:

  • 如果失衡節點的右孩子的平衡因子 < 0，則是RR型失衡。

  • 如果失衡節點的右孩子的平衡因子 > 0，則是RL型失衡。

// curr節點失衡了, 需要進行調整
// bf是這個節點的平衡因子
if (bf > 1) // 失衡節點的平衡因子>1，說明左子樹比較高，因此找失衡節點的左孩子
{
    // 看失衡節點左孩子的平衡因子
    int leftBf = balanceFactor(curr->left);
    if (leftBf > 0) // 這個左孩子的左子樹高於右子樹
    {
        // 這說明是LL型，即插入在失衡節點【左孩子的左子樹中】而導致失衡，需要進行「右旋」進行調整
        rotateRight(curr);
    }
    else // 這個左孩子的右子樹高於左子樹
    {
        // 這說明是LR型，插入在失衡結點【左孩子的右子樹中】而導致失衡，需要進行「左旋再右旋」進行調整
        rotateLeft(curr->left); // 先對左孩子進行左旋
        rotateRight(curr);      // 再對失衡節點進行右旋
    }
}
else if (bf < -1) // 失衡節點的平衡因子<-1，說明右子樹比較高，因此找失衡節點的右孩子
{
    int rightBf = balanceFactor(curr->right);
    if (rightBf < 0) // 右孩子的右子樹高於左子樹
    {
        // 這說明是RR型，即插入在失衡節點【右孩子的右子樹中】，需要進行「左旋」進行調整
        rotateLeft(curr);
    }
    else // 右孩子的左子樹高於右子樹
    {
        // 這說明是RL型，即插入在失衡節點【右孩子的左子樹中】，需要進行「右旋再左旋」進行調整
        rotateRight(curr->right); // 先對右孩子進行右旋
        rotateLeft(curr);         // 再對失衡節點進行左旋
    }
}

插入後一定要回溯到根節點嗎？

本文開頭咱簡述了一下AVL樹的插入操作。

在往AVL樹中插入了一個節點後，需要沿著祖先節點向上回溯到根節點，沿途更新每個節點的高度，並尋找失衡的節點來進行調整。

節點的高度用於計算平衡因子。

遇到平衡因子為0的節點時回溯可以停止