[資料結構] 二元搜尋樹 (二叉排序樹)
二元搜尋樹
二元搜尋樹的基本概念
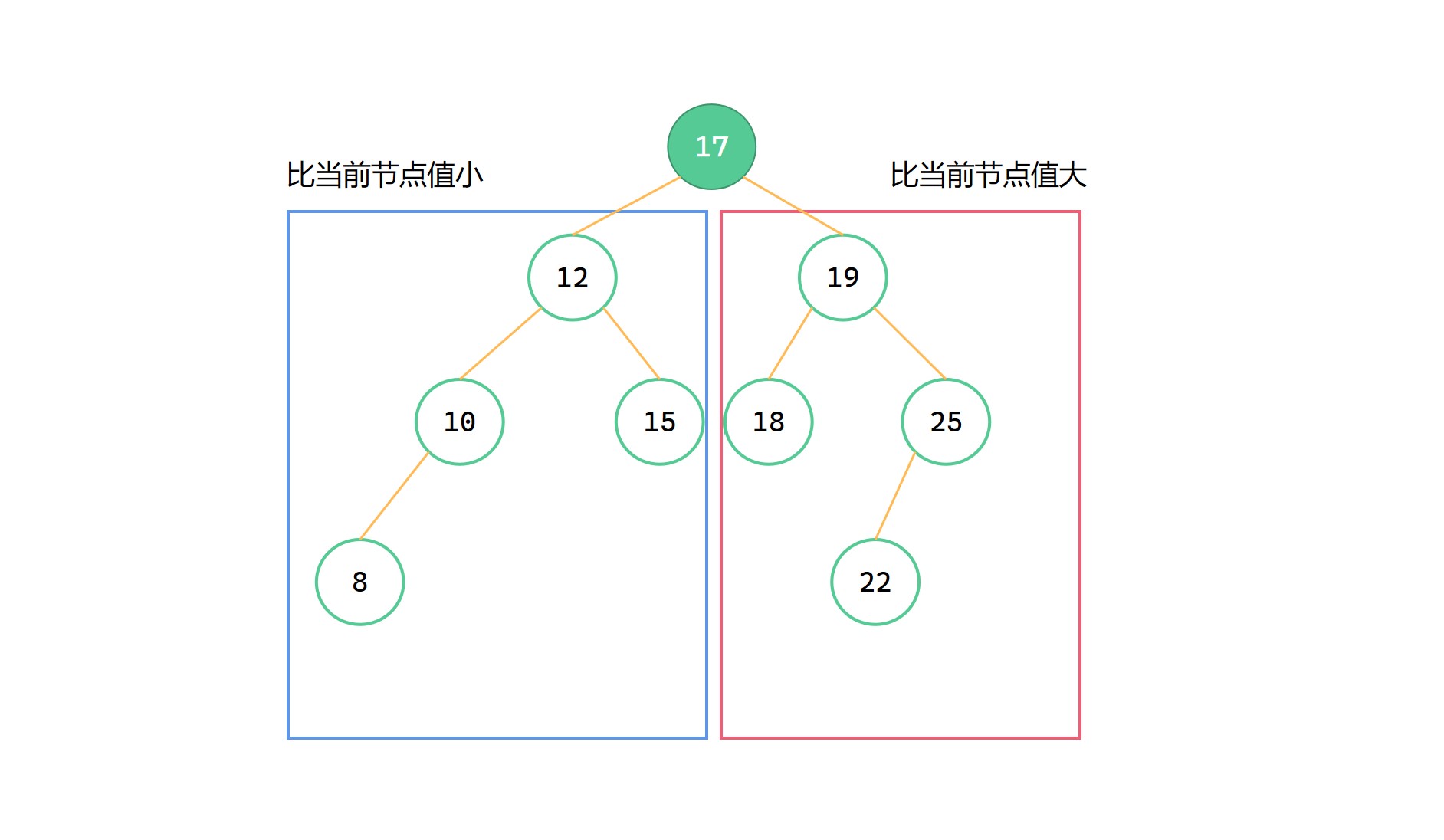
二元搜尋樹( Binary Search Tree )也稱二叉排序樹,是一種各節點值之間存在一定次序關係的二元樹。
二元搜尋樹的特點
一般情況下,二元搜尋樹中所有節點值是不重複的。
對於二元搜尋樹中的每個節點:
(1)如果其左子樹不為空,那麼其左邊的節點值都比當前節點值小;
(2)如果其右子樹不為空,那麼其右邊的節點值都比當前的節點值要大。
二元搜尋樹的中序遍歷結果,就是所有節點值升序排序的結果。
二元搜尋樹的查詢
二元搜尋樹查詢的基本步驟
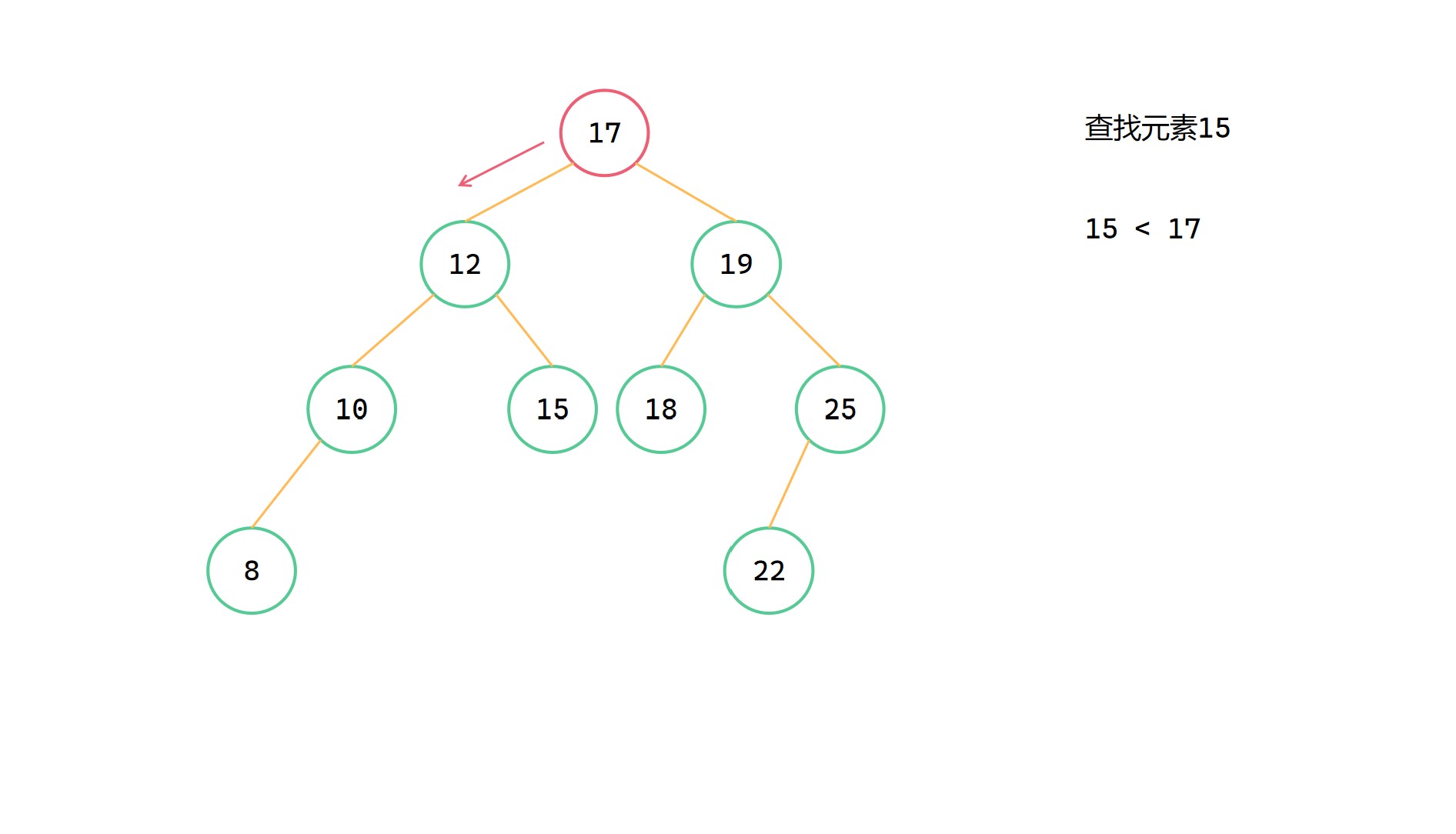
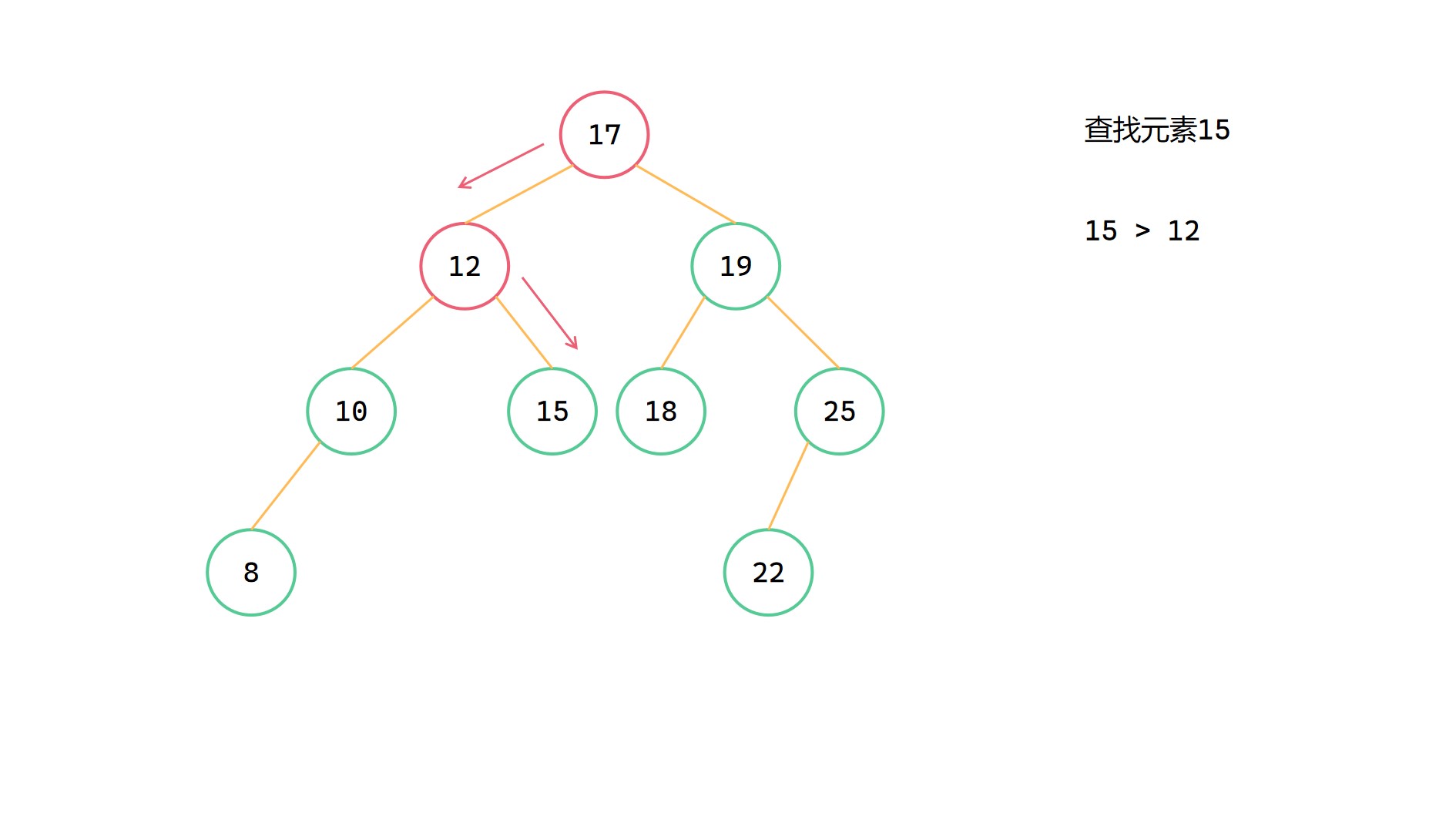
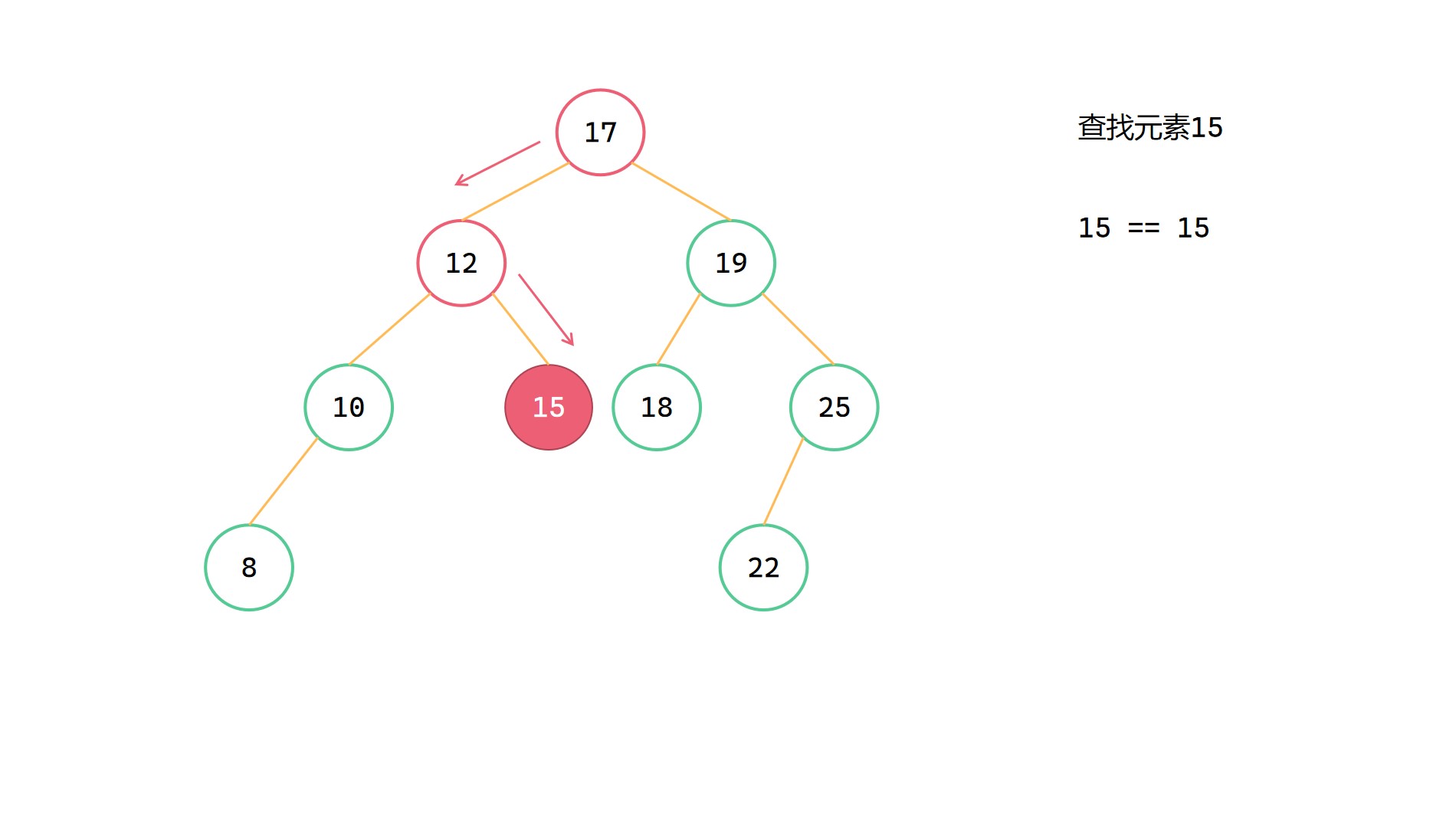
根據二元搜尋樹的特點,其實二元搜尋樹中的查詢和二分查詢非常相似。從樹的根節點出發,當前節點值 val 如果等於目標值 target,那麼就直接返回;如果 val 小於目標值 target,那麼就要往左邊去尋找;如果 val 大於目標值 target,那麼就要往右邊去尋找。假如最後節點為 NULL,都沒有找到等於目標值的節點,那麼說明此時的二元搜尋樹中不存在這個等與目標值 target 的節點。
我們將使用遞迴函數來實現這一過程,假設函數名為 SearchBST,則大致步驟為:
(1)節點為空,沒有等於目標值的節點 if(!root) return NULL ;
(2)當前節點值小於目標值 if(root->val < target) return SearchBST(root->left) ;
(3)當前節點值大於目標值 if(root->val > target) return SearchBST(root->right) ;
(4)找到該節點 return root 。
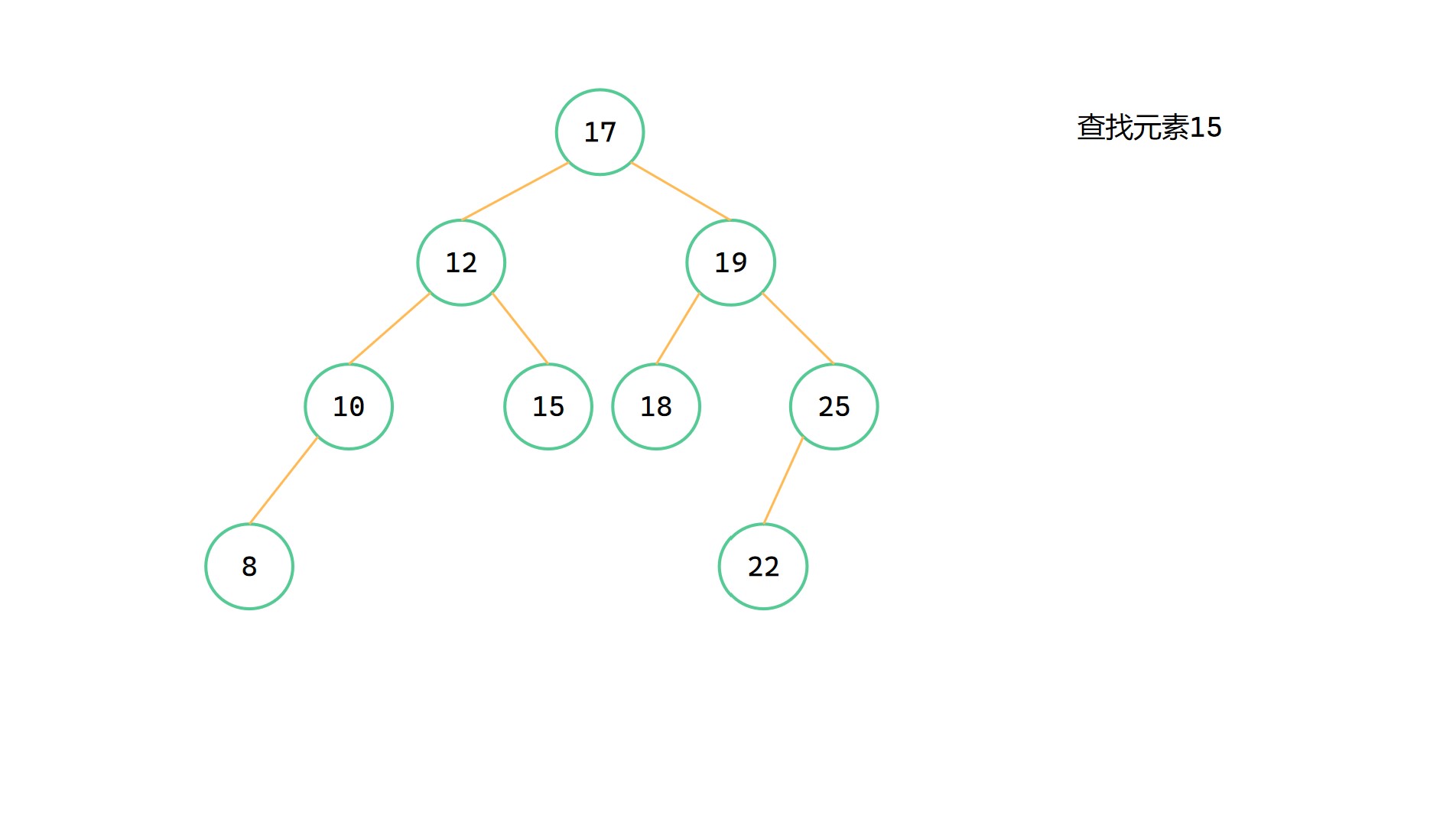
二元搜尋樹查詢圖解
(1)
(2)
(3)
(4)
二元搜尋樹查詢程式碼
//遞迴 查詢二叉排序樹指定元素target
BinaryTree Search_BST(BinaryTree root, Elemtype target){
if(!root) //最後沒有找到root為NULL
return NULL;
if(target > root->val) //root值小於target 往其右子樹查詢
return Search_BST(root->rightchild, target);
if(target < root->val) //root值大於target 往其左子樹查詢
return Search_BST(root->leftchild, target);
return root; //找到直接返回該節點
}
二元搜尋樹的插入
二元搜尋樹插入的基本步驟
二元搜尋樹插入的元素,首先一定是當前二元搜尋樹中不存在的元素,如果要插入的元素 val 已經存在於二元搜尋樹中,那麼就沒有插入的必要了。
二元搜尋樹插入新元素,同時還需要使整棵樹保持二元搜尋樹的性質。所以在插入過程中,我們依舊需要用類似於二分查詢的形式來實現插入的操作。從樹的根節點出發,如果當前節點為空,說明可以插入到這個位置;如果插入元素 val 與當前節點值相等,說明已經存在,直接 return;如果插入元素 val 小於當前節點值,那麼遞迴往左尋找合適的插入位置;如果插入元素 val 大於當前節點值,那麼遞迴往右尋找合適的插入位置。
我們還是用遞迴函數來實現這個插入的過程,也是建立二元搜尋樹的過程。
假定函數名為 InsertBST ,則大致步驟為:
(1)當前節點位置為空,可以插入,建立一個新節點 root = new Node(val) ;
(2)當前節點值與插入元素值相等,直接 return;
(3)插入元素 val 小於當前節點值,則進行 InsertBST(root->left, val) ;
(4)插入元素 val 大於當前節點值,則進行 InsertBST(root->right, val) 。
二元搜尋樹插入圖解
(1)
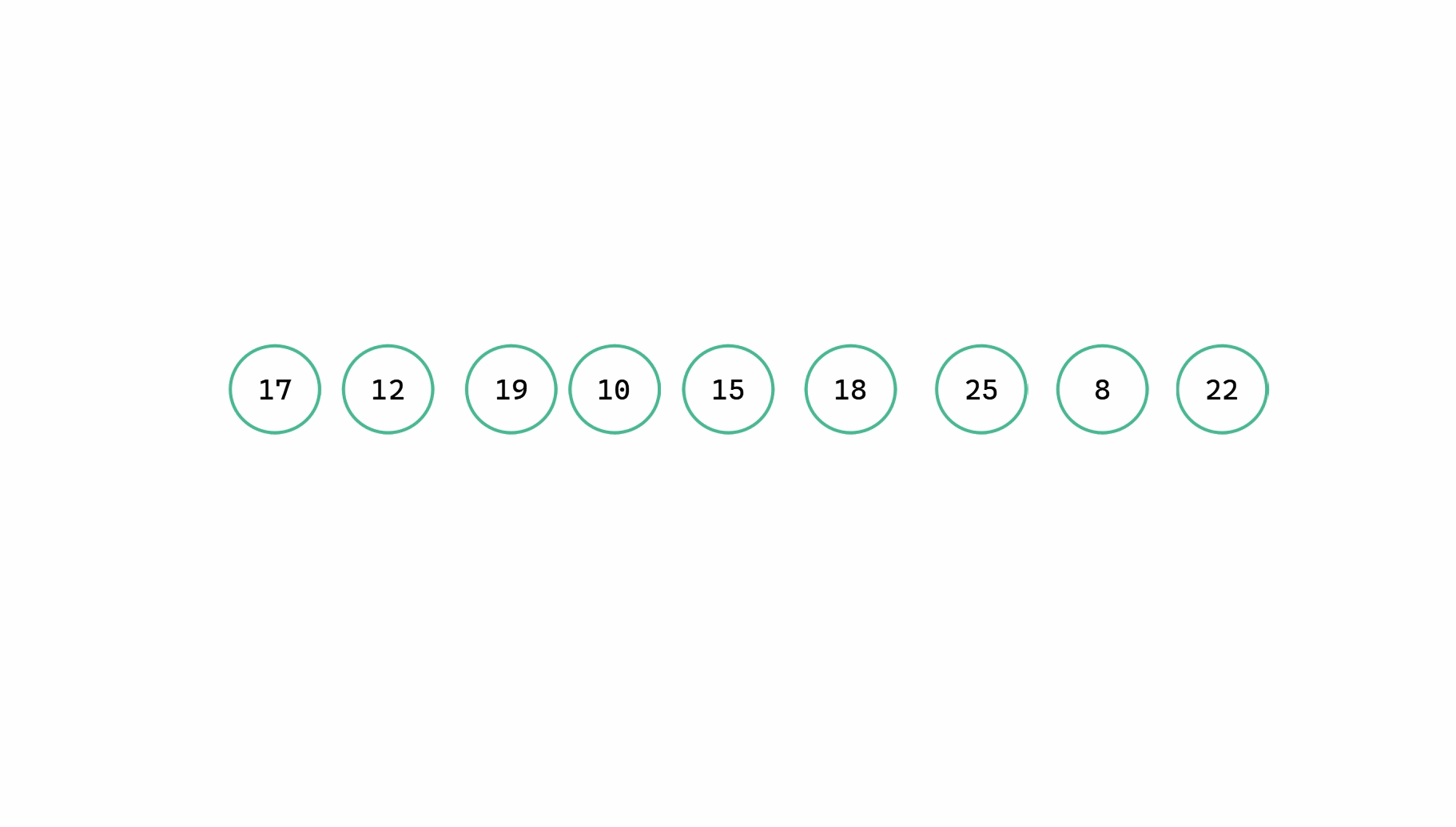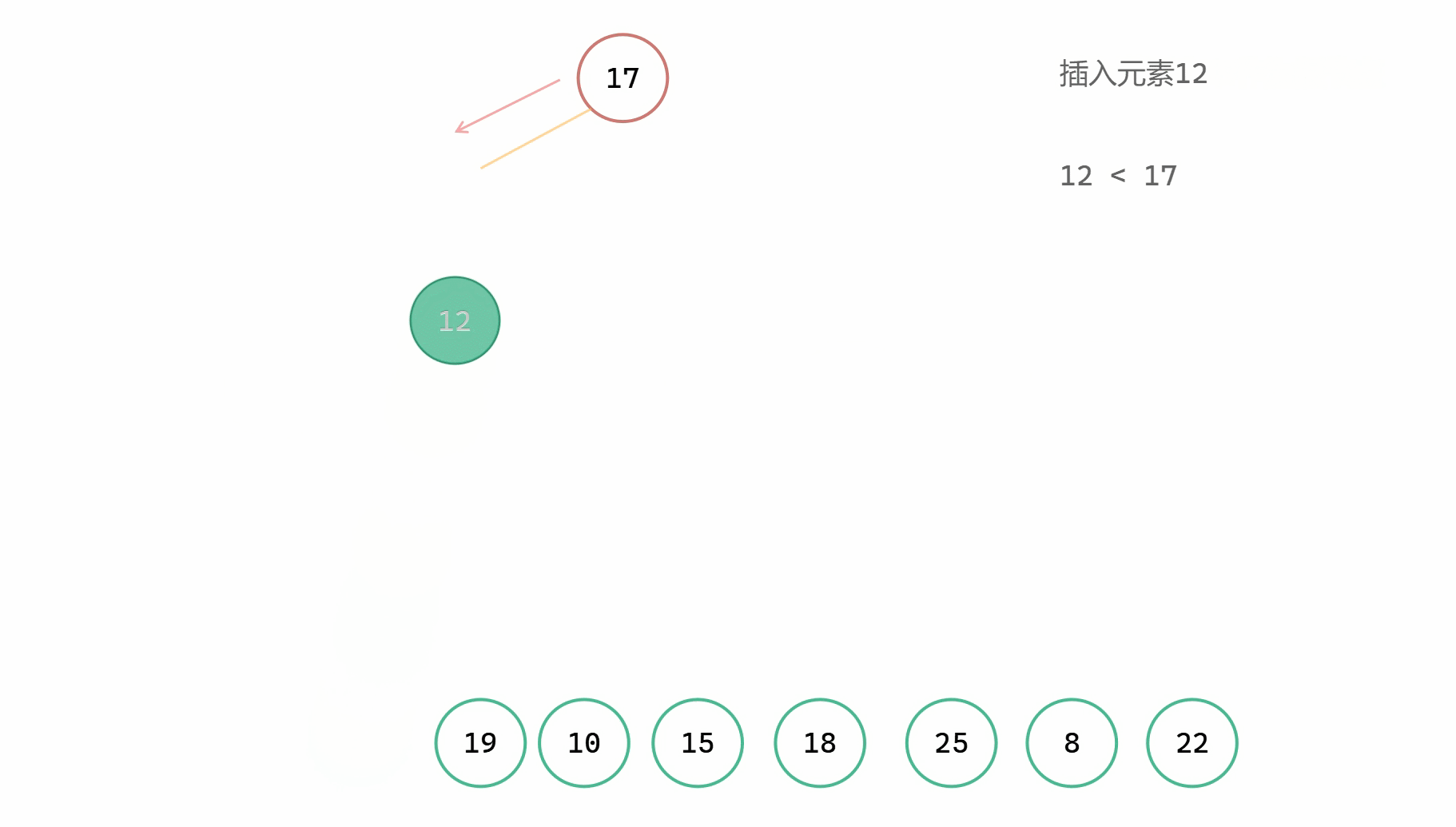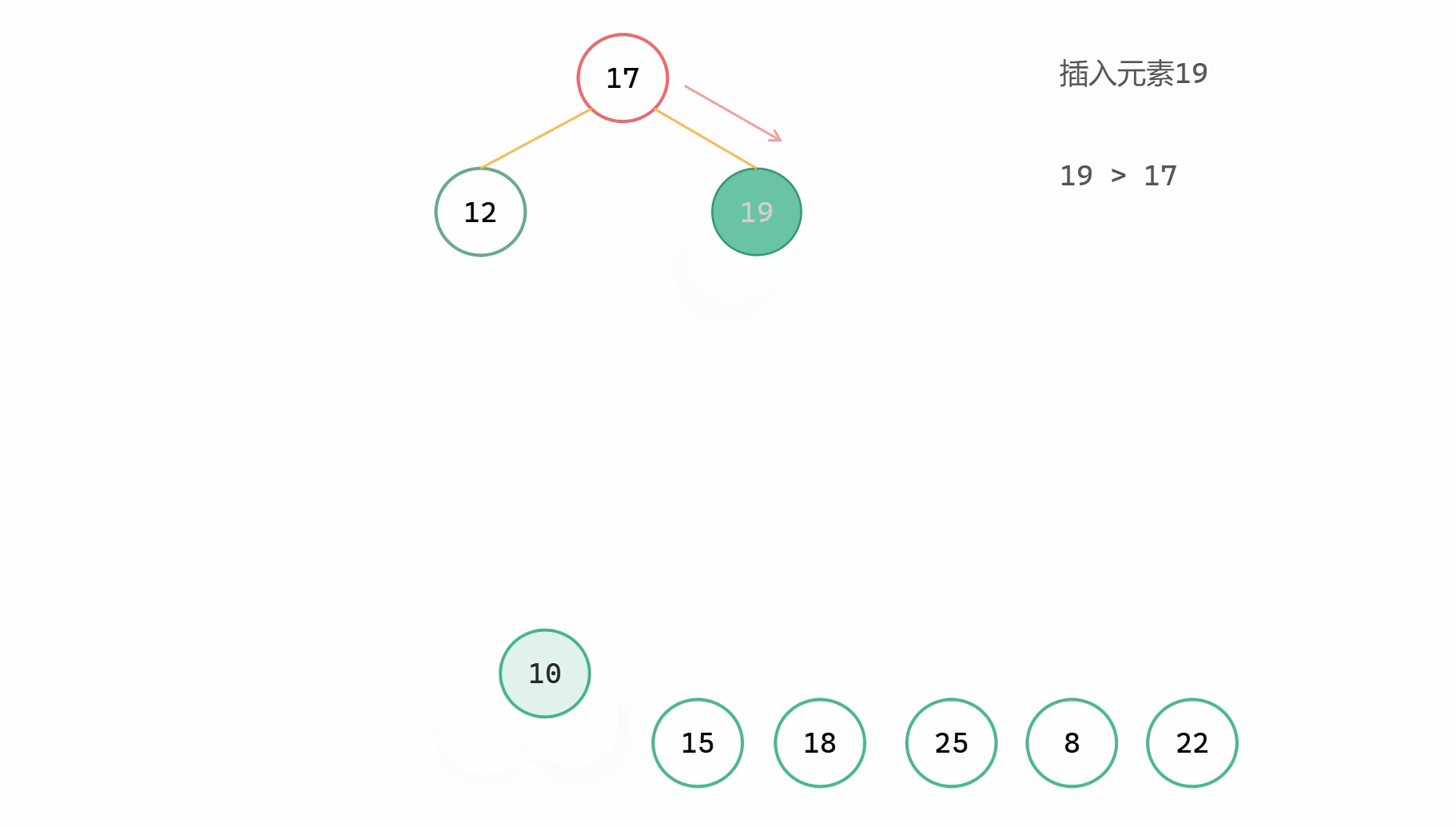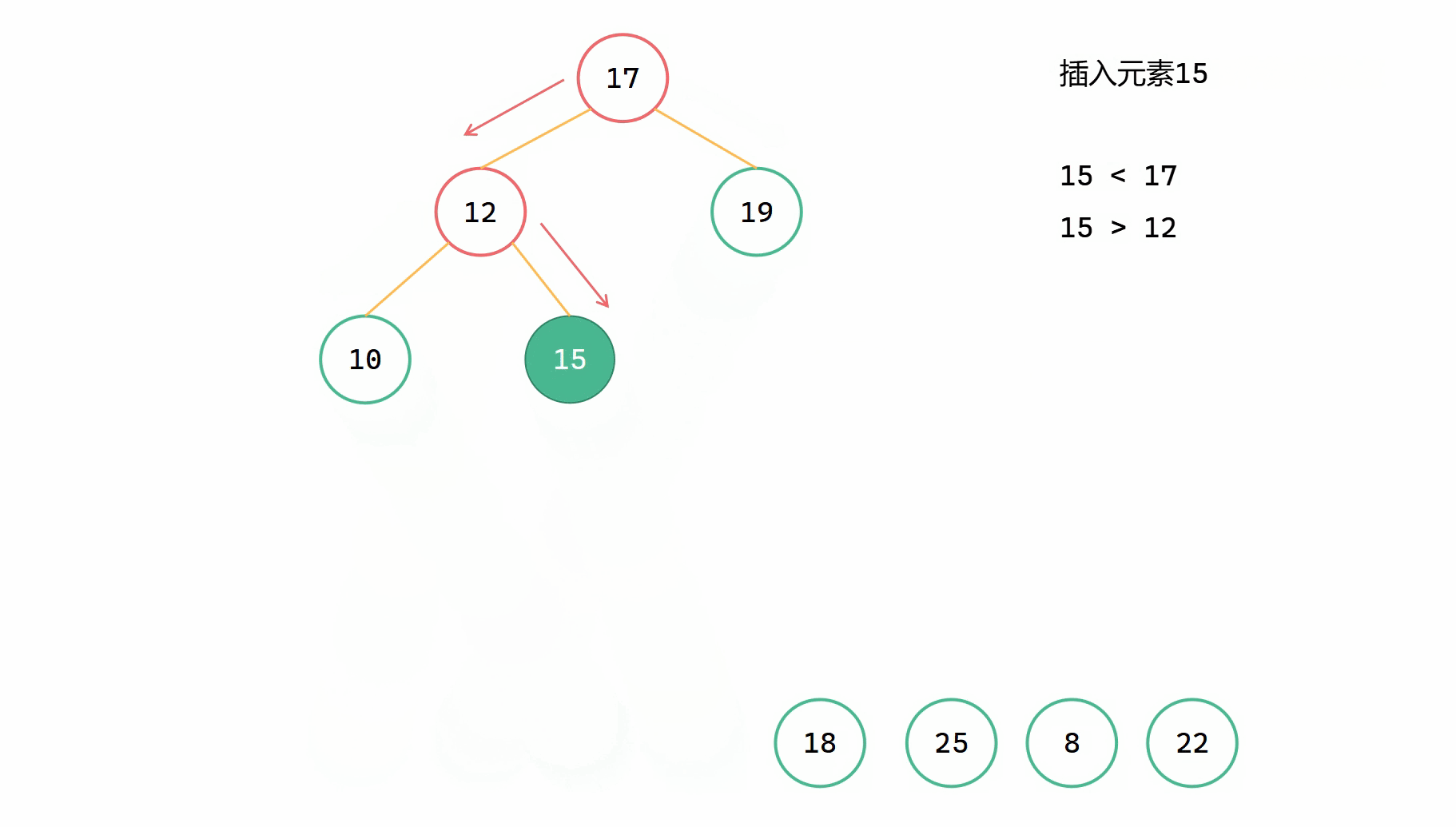
(2)
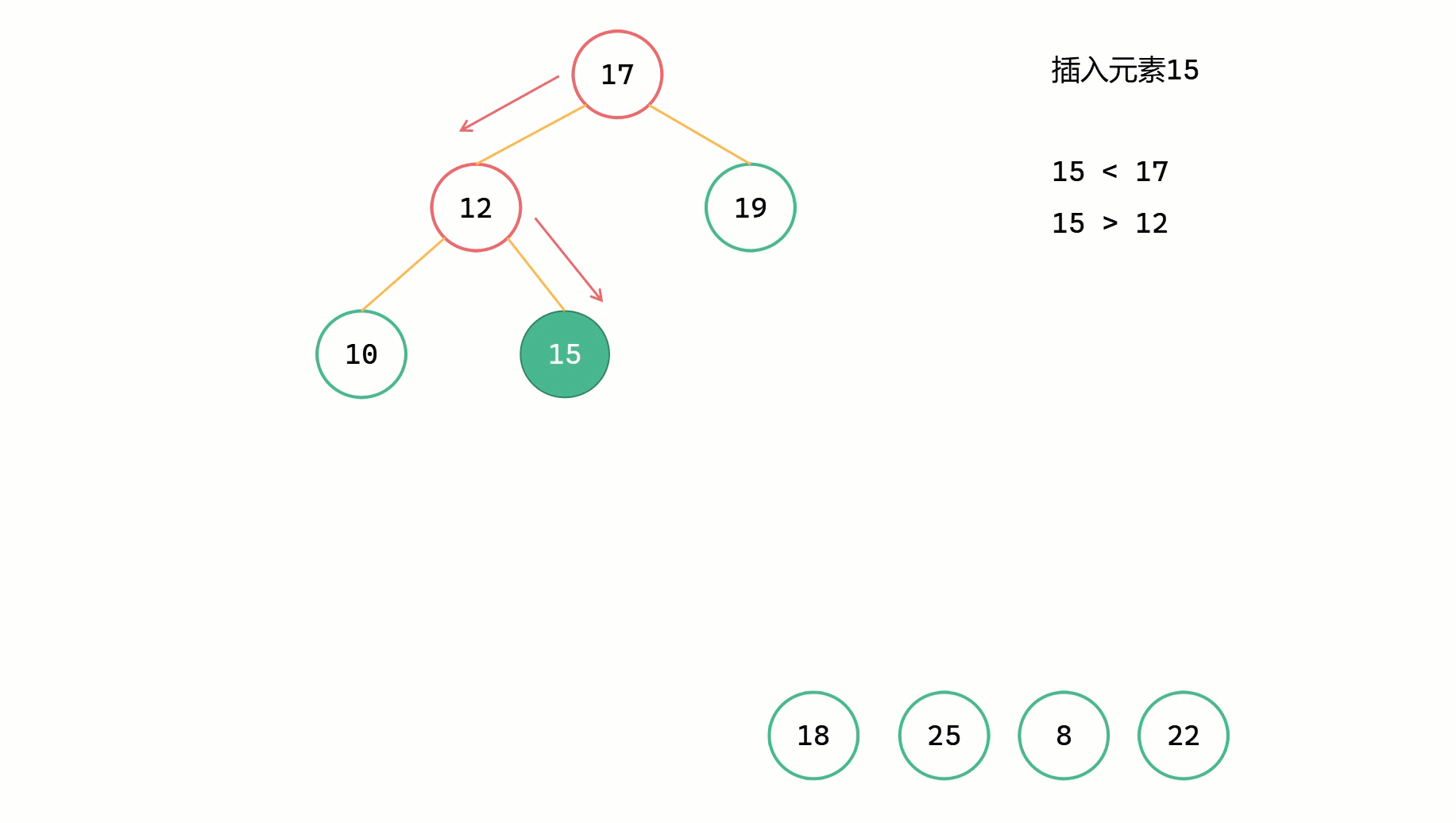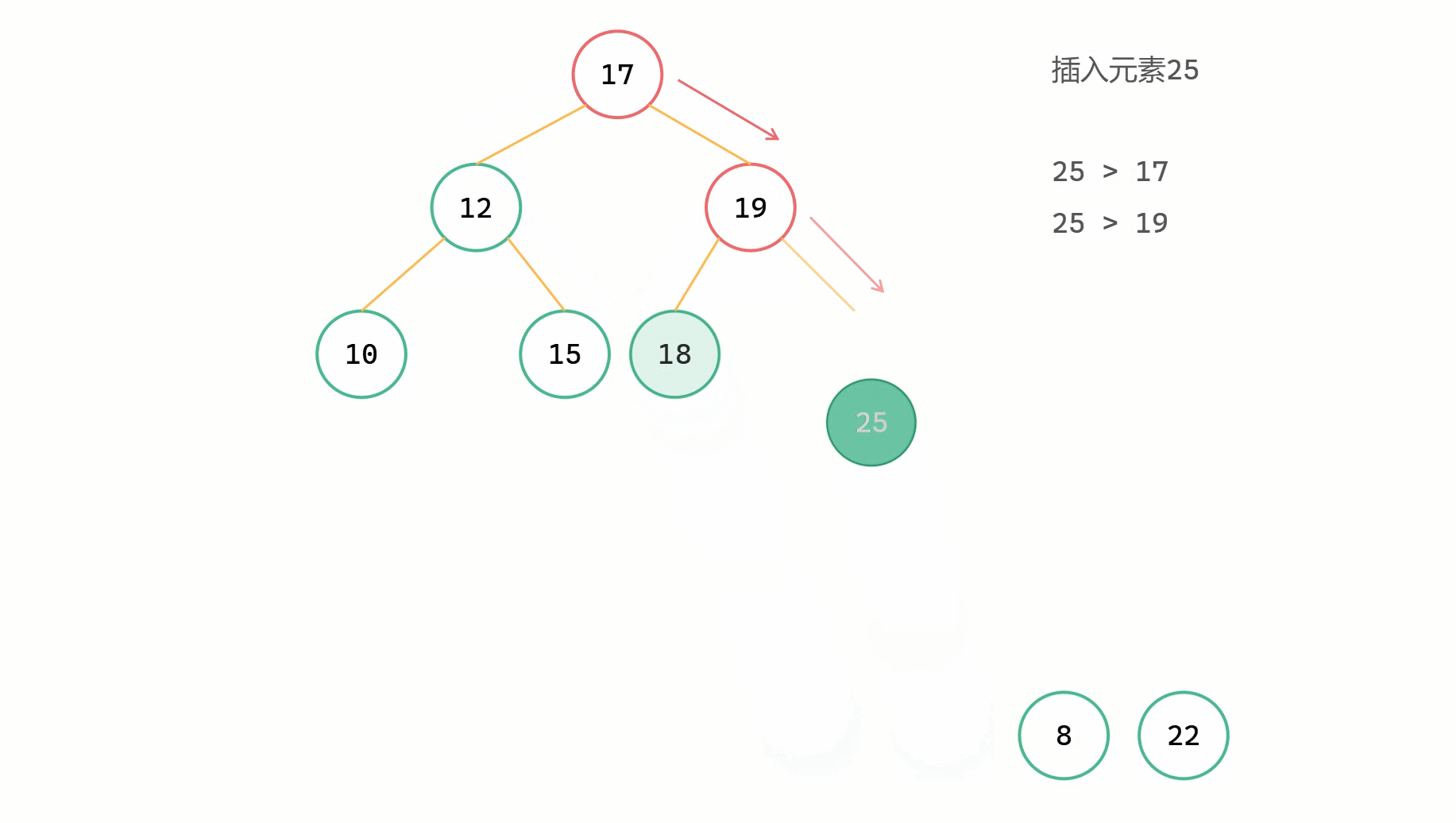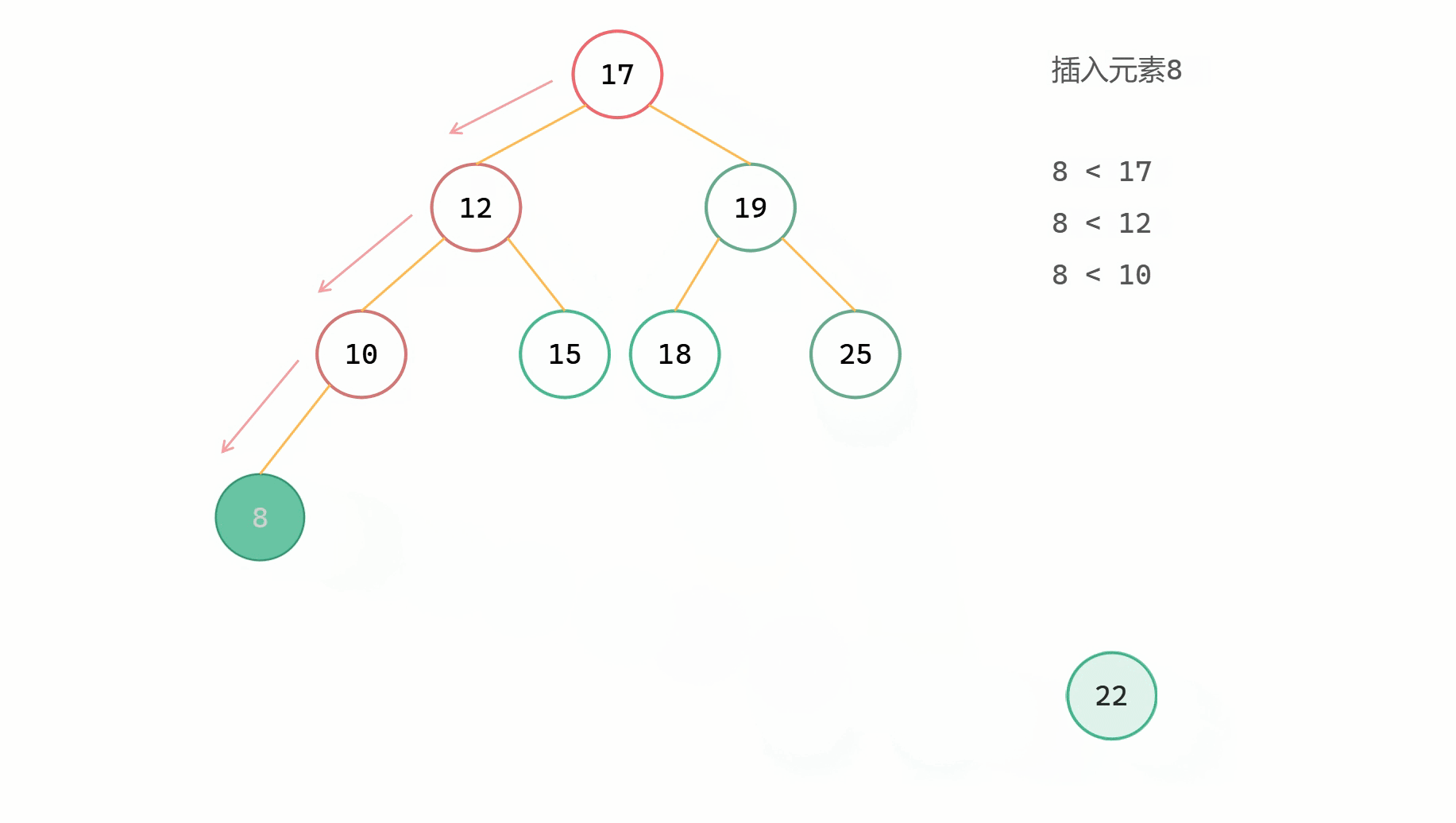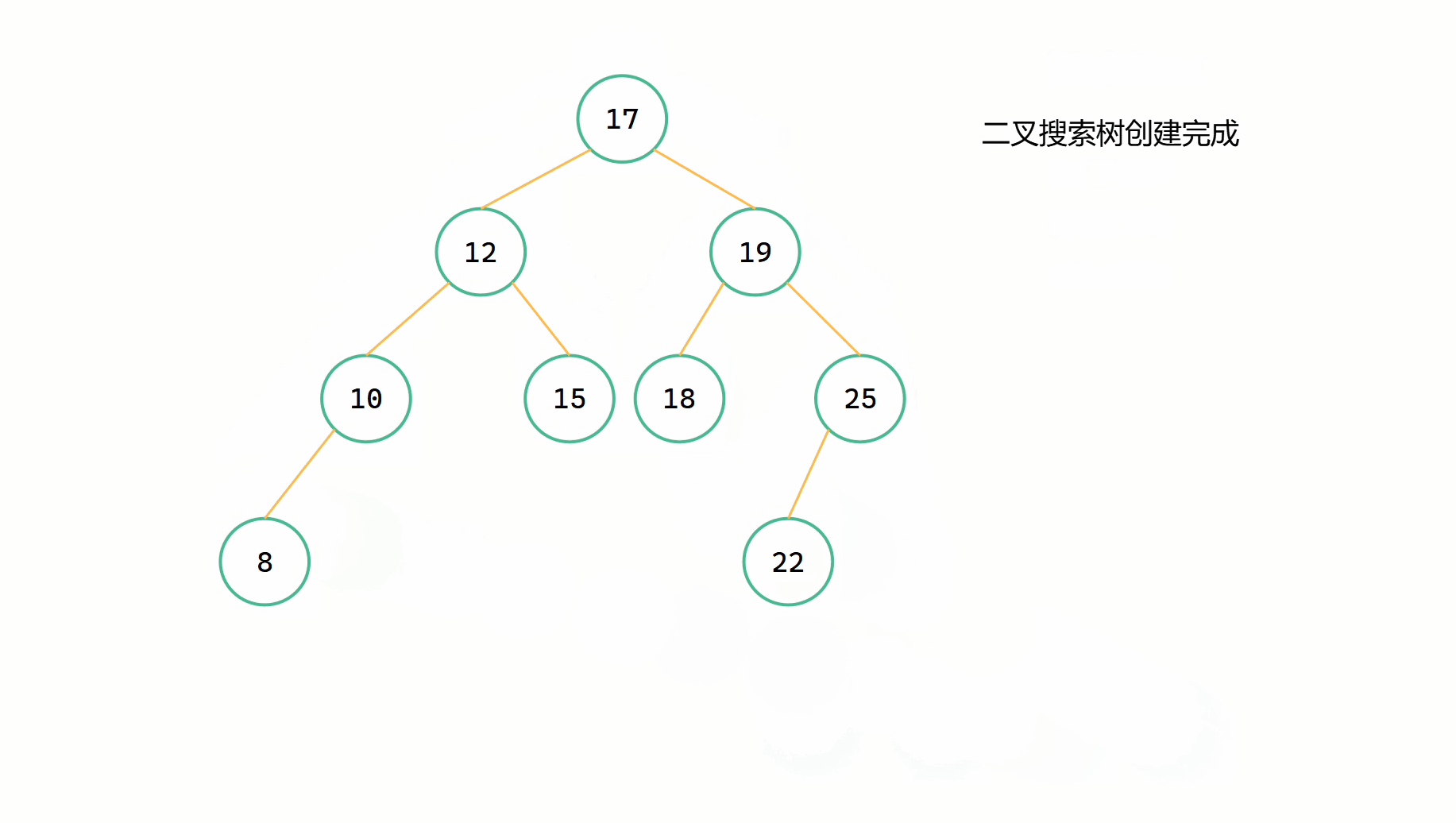
二元搜尋樹插入程式碼
//二叉排序樹元素的插入
void Insert_BST(BinaryTree &root, Elemtype val){
if(!root){ //若為當前root為空
BinaryTree node = (BinaryTree)malloc(sizeof(BiNode));
node->val = val;
node->leftchild = node->rightchild = NULL;
root = node;
return;
}
if(root->val == val)
return; //當前值已經存在 則不插入
/* 遞迴寫法 */
if(root->val > val)
Insert_BST(root->leftchild, val);
else
Insert_BST(root->rightchild, val);
}
二元搜尋樹的刪除
第一類刪除的情況
刪除節點為葉子結點
基本步驟
由於刪除節點為葉子結點,直接置 NULL 即可,刪除完之後不會對整棵樹滿足二元搜尋樹性質產生任何影響。
圖解
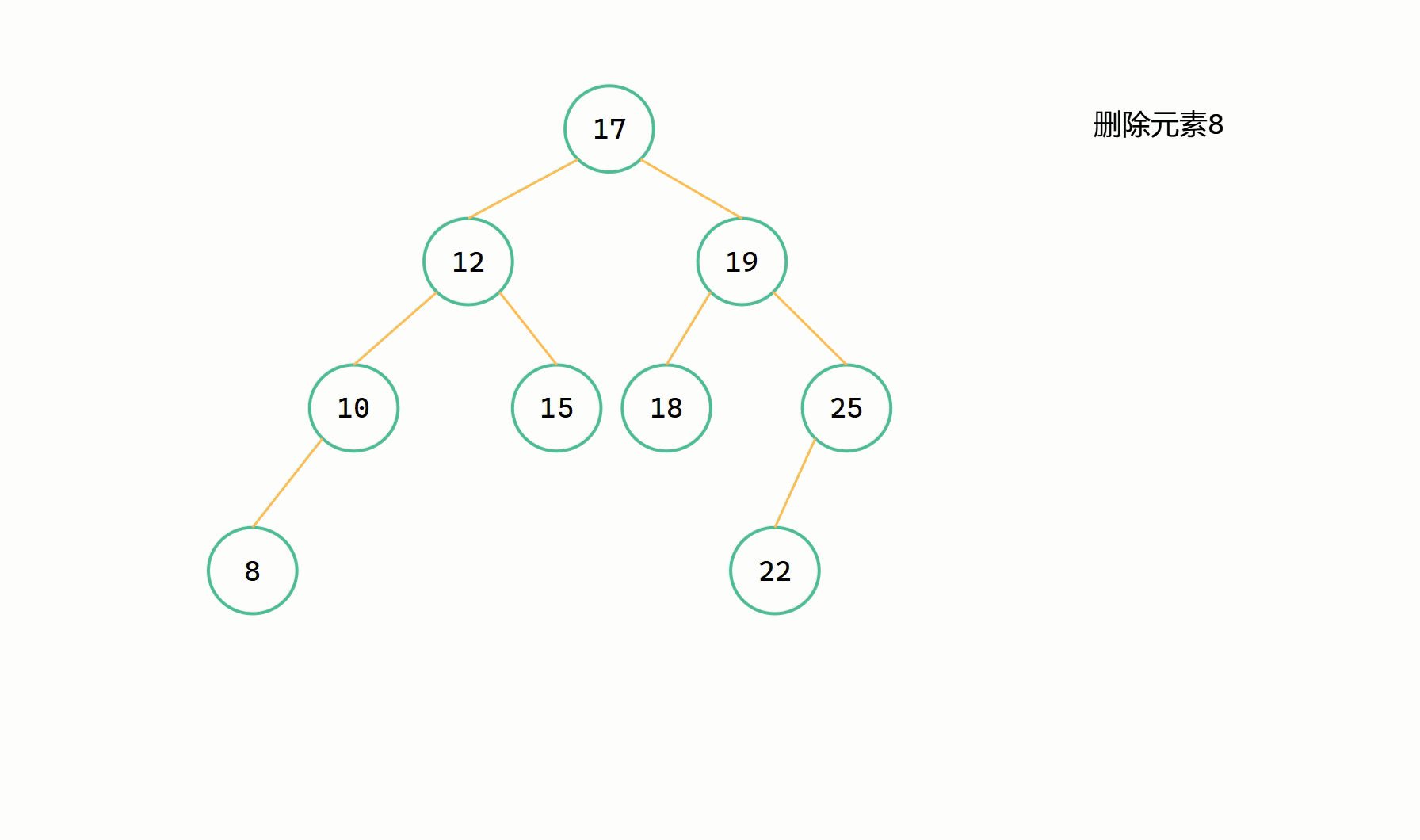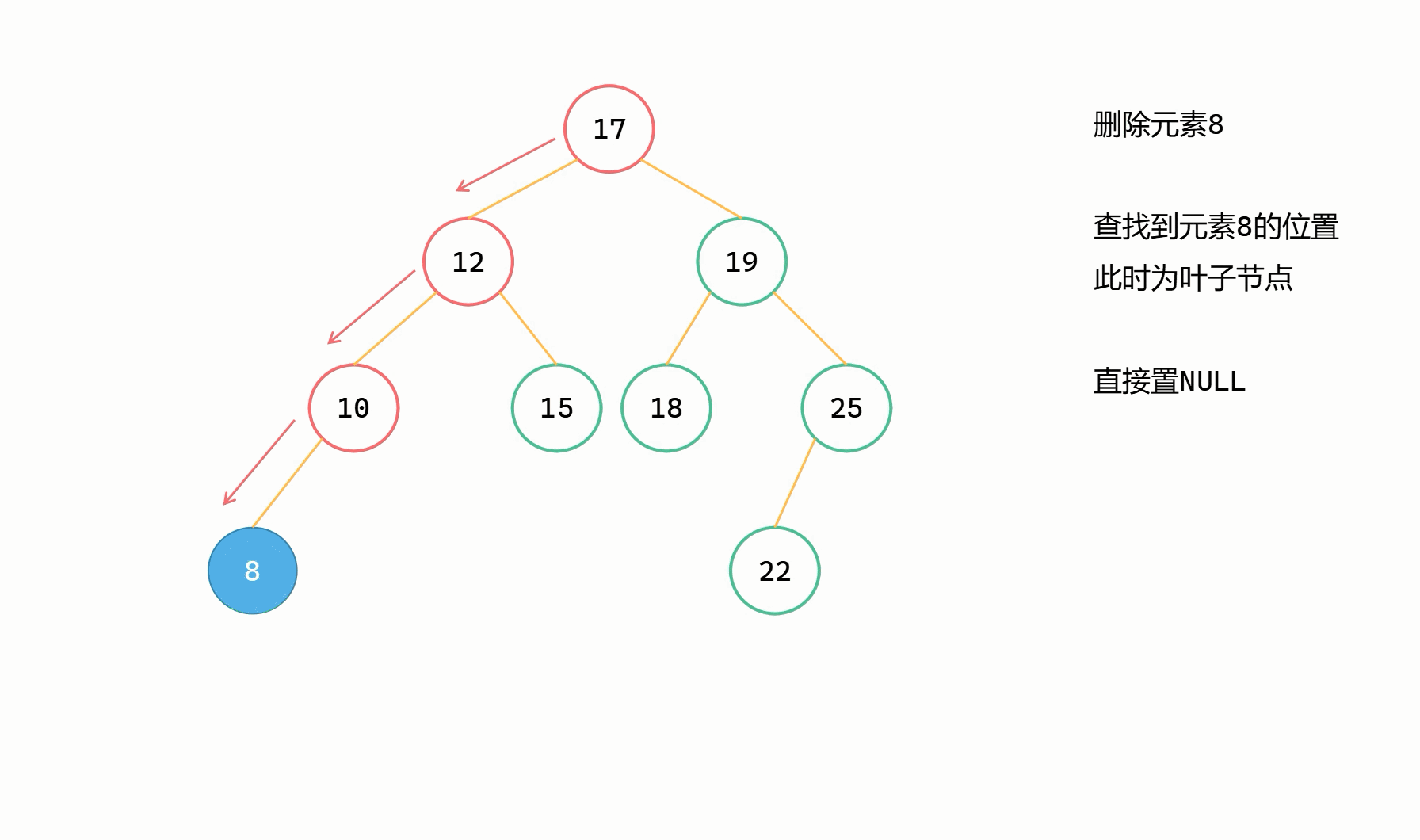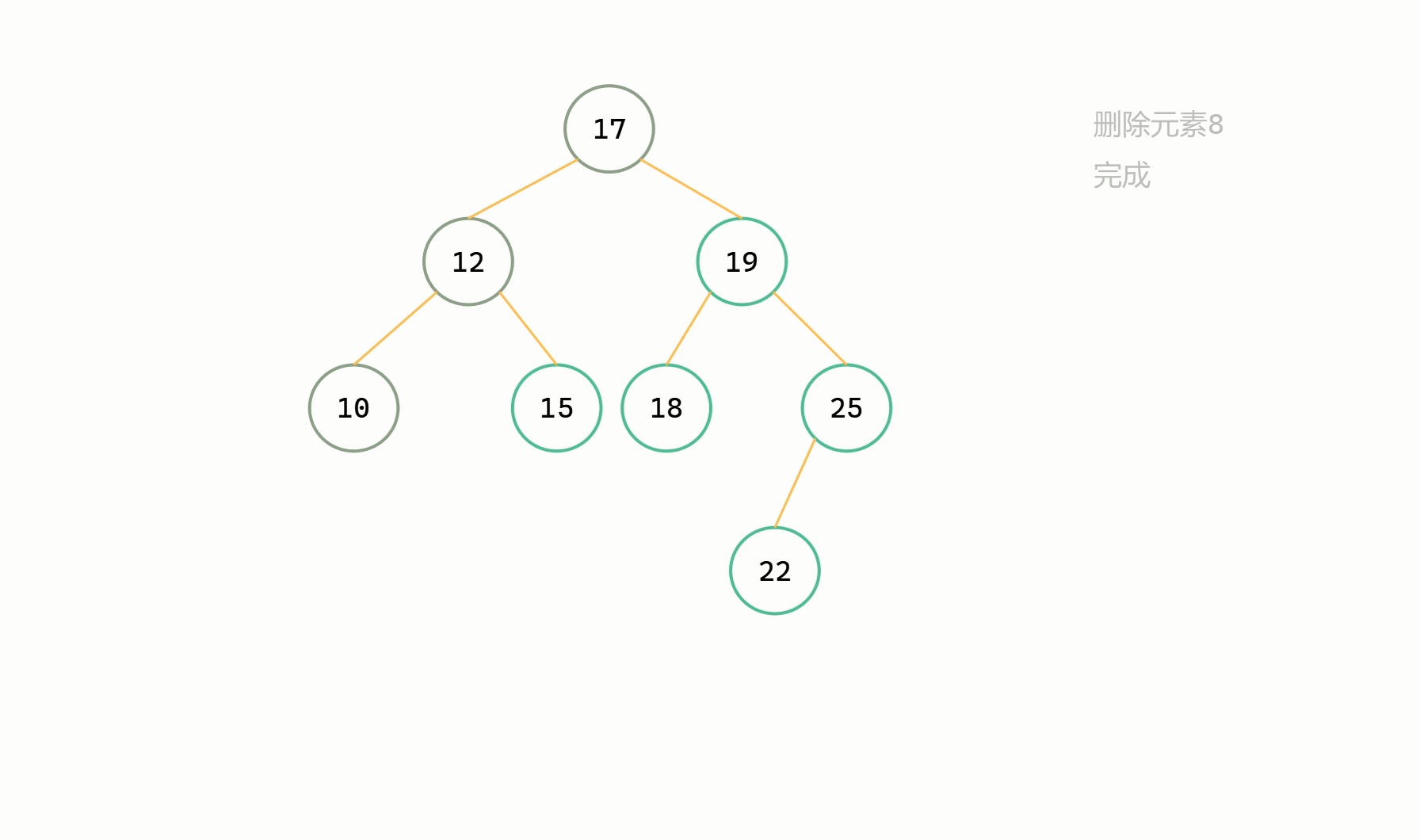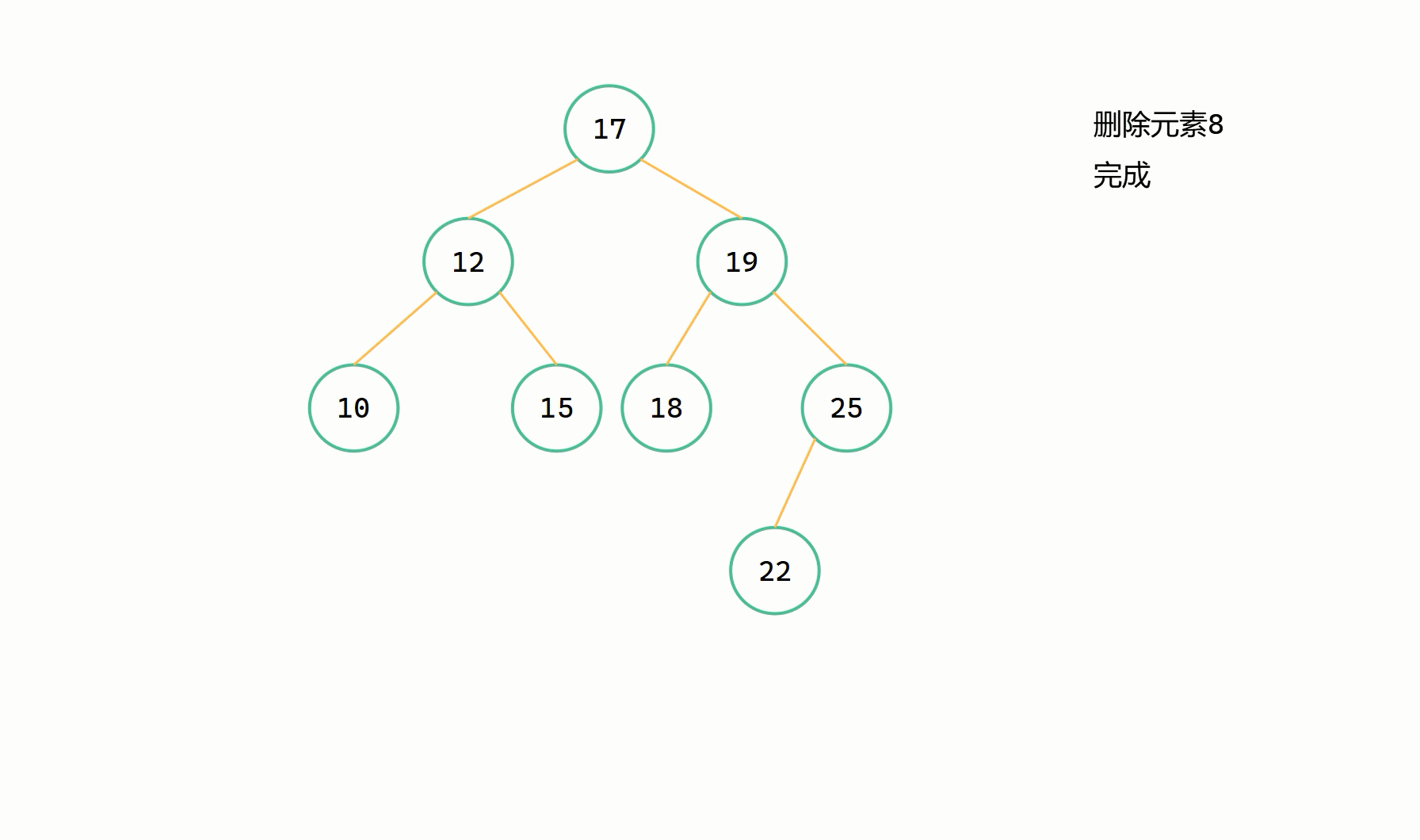
第二類刪除的情況
這一類刪除的節點的特點為其只有一個子樹,另一個子樹為空。這種情況往往也是比較方便處理的。
(1)刪除節點只有右子樹
當刪除節點只有右子樹時,為了維持二元搜尋樹的特點,只需要將刪除節點的右子樹繼承給其父節點就可以,並且做到了將該節點刪除。
基本步驟
假定 root 為當前要刪除的節點,直接 root = root->right。
圖解
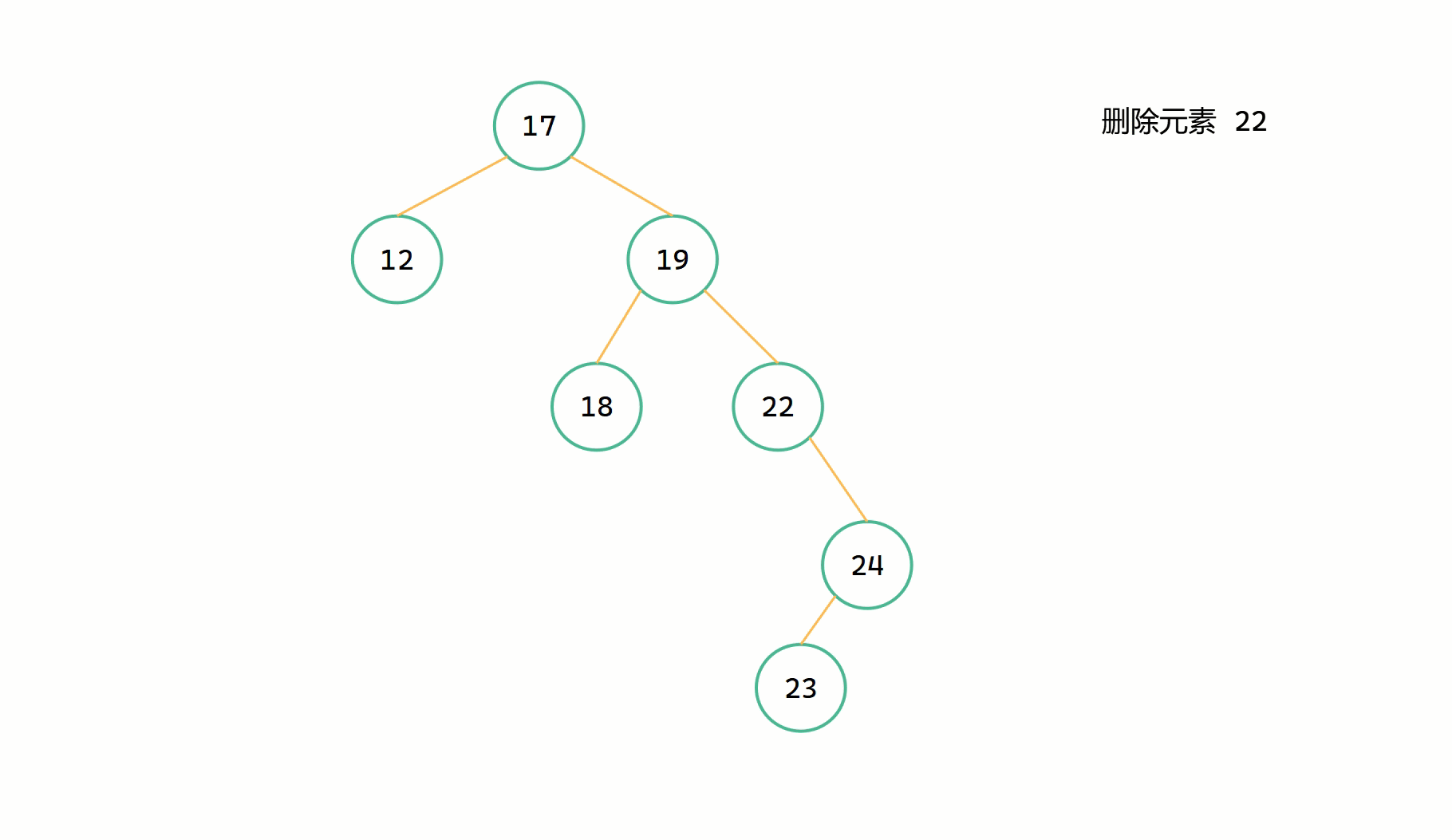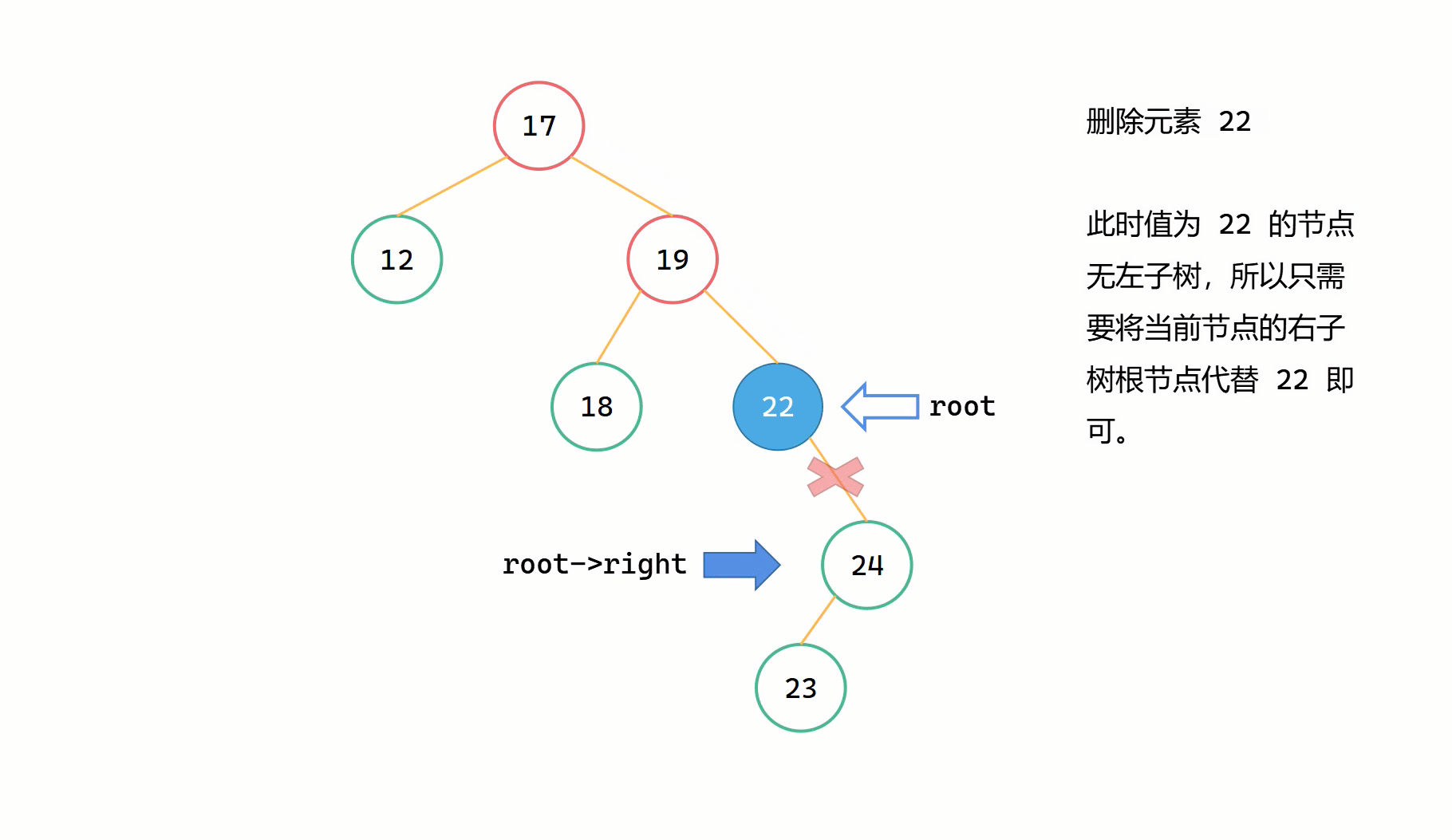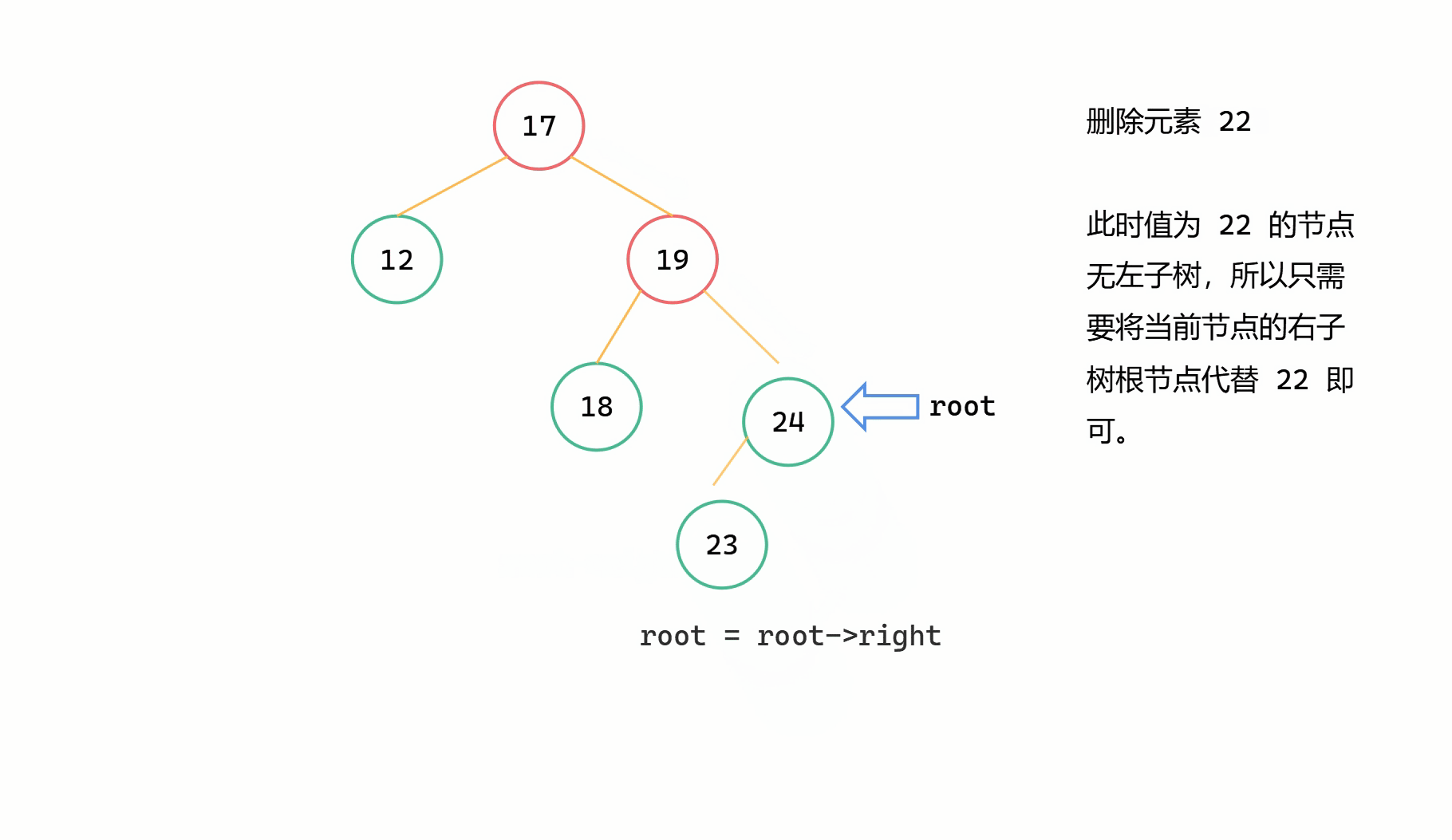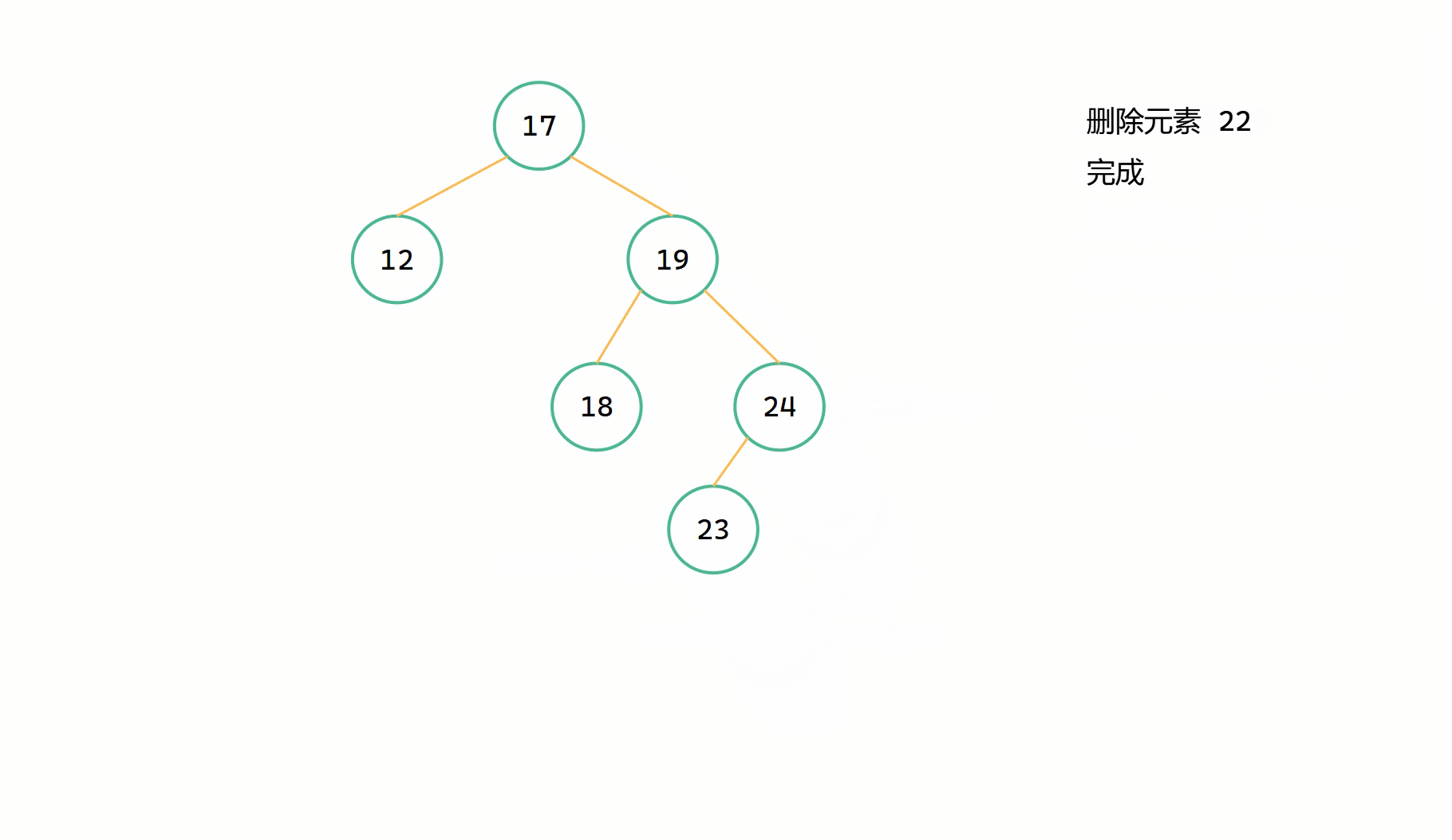
(2)刪除節點只有左子樹
當刪除節點只有左子樹時,為了維持二元搜尋樹的特點,和上一種情況也類似,將左子樹繼承給其父節點。
基本步驟
假定 root 為當前要刪除的節點,直接 root = root->left。
圖解
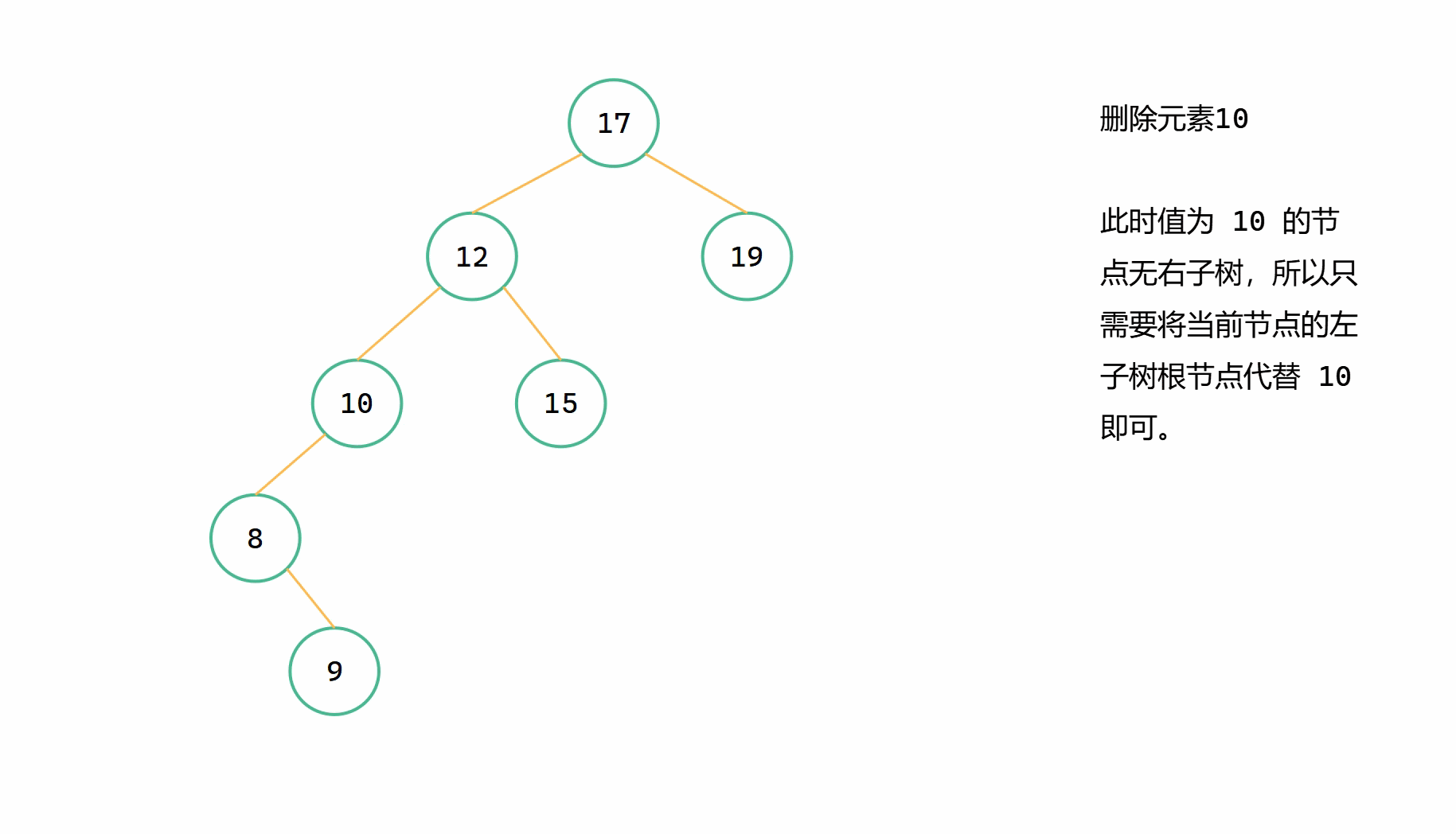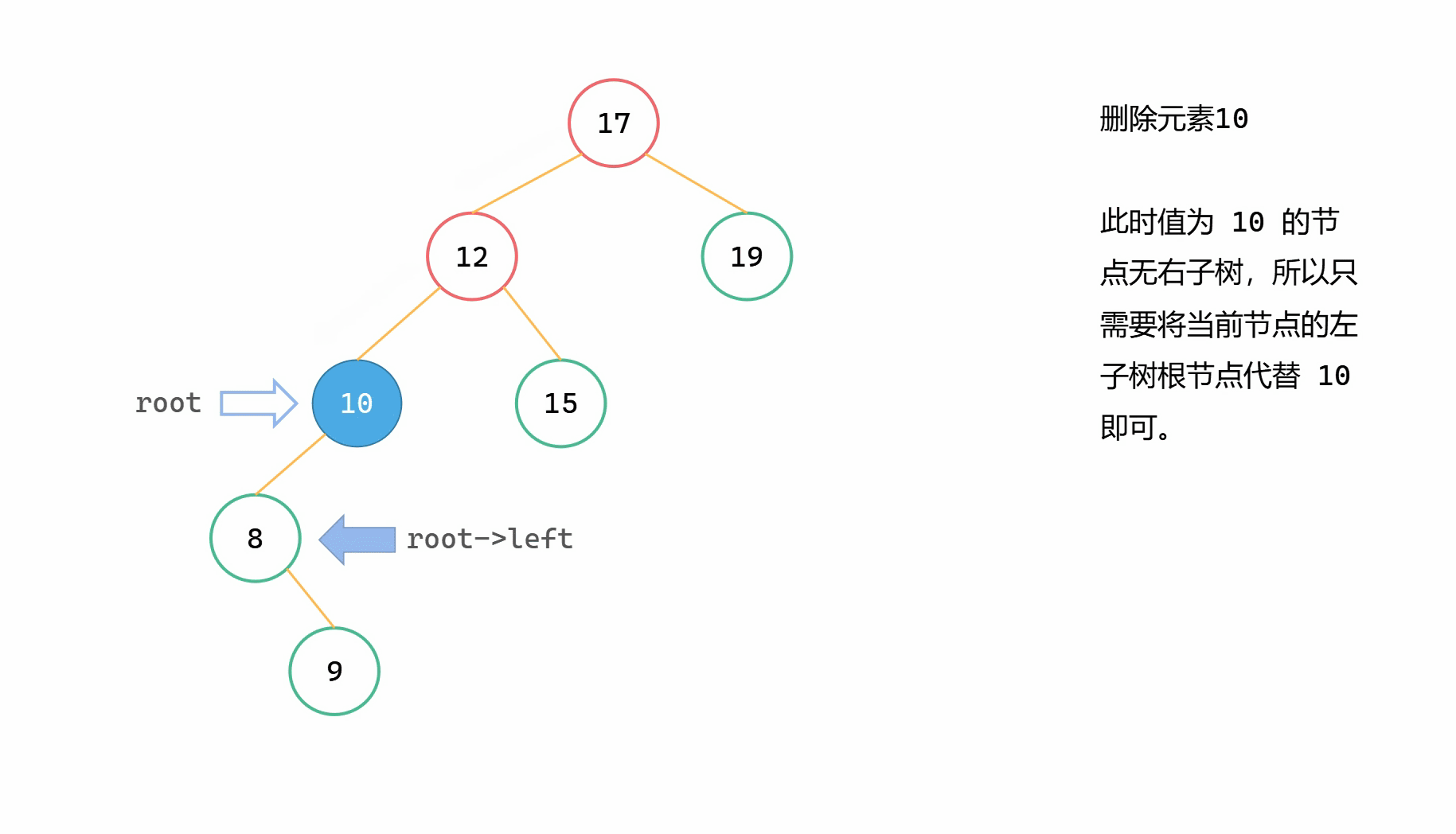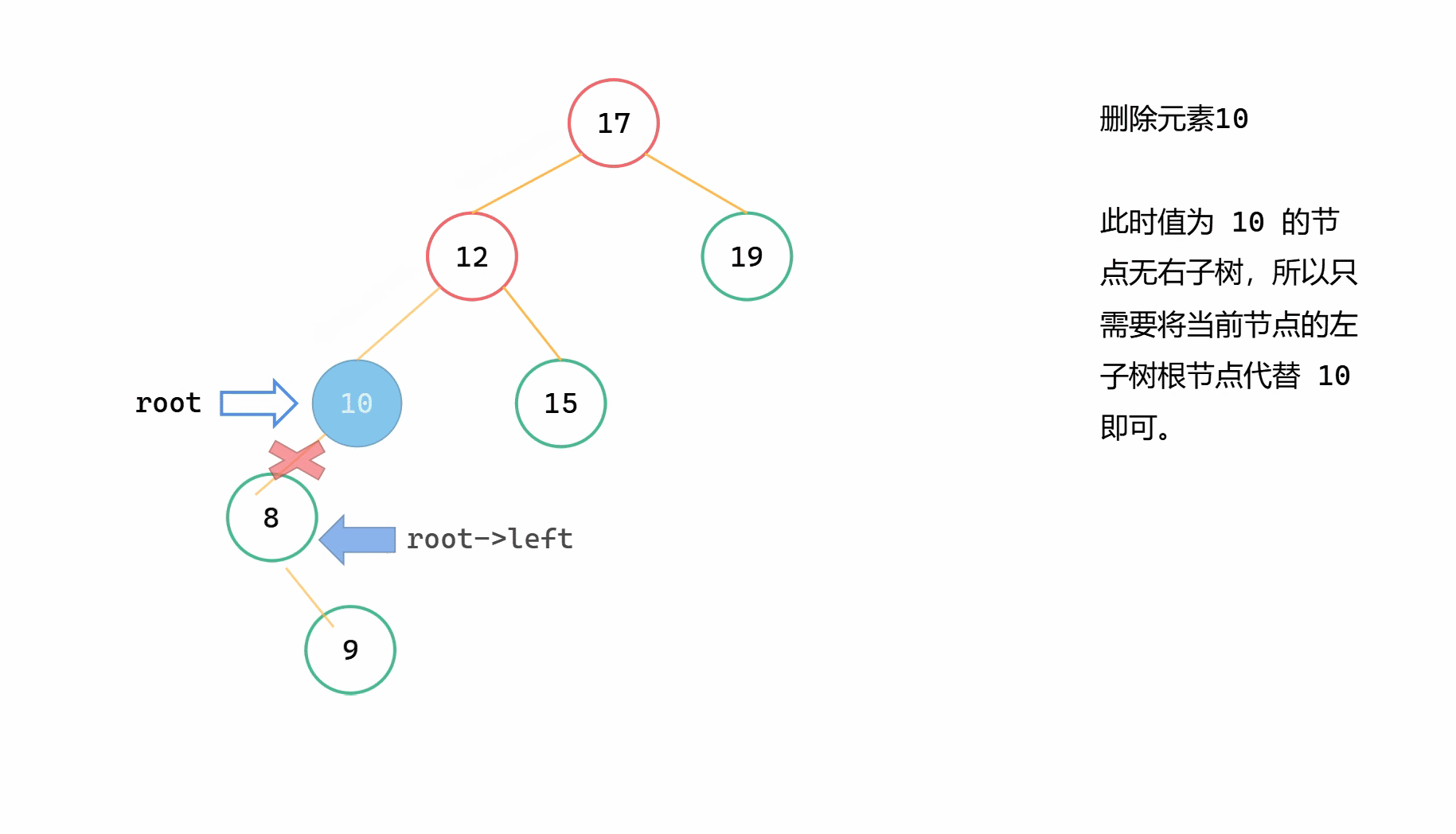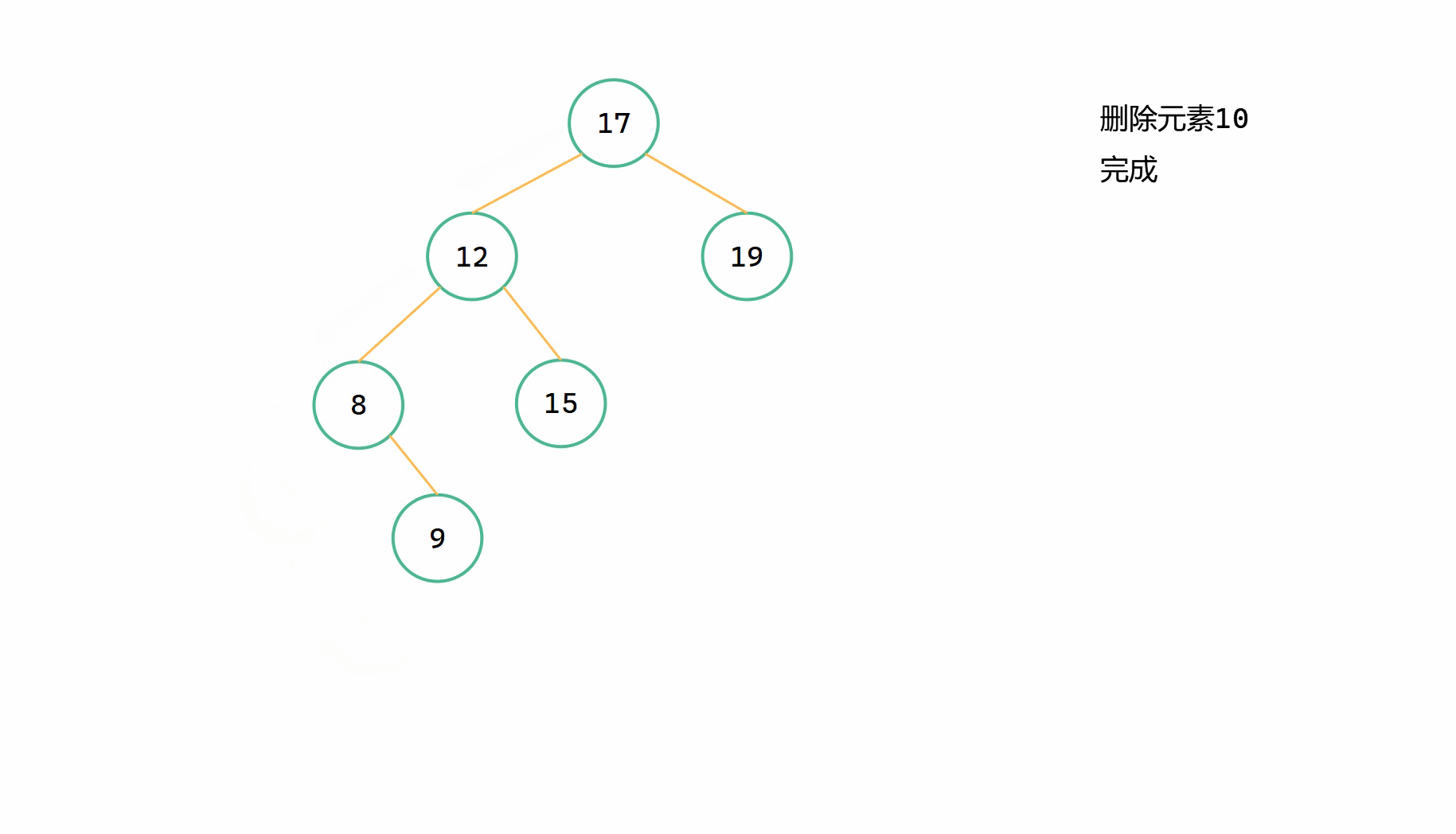
第三類刪除的情況
這一類刪除的節點同時含有左子樹和右子樹,此時的處理是比較麻煩的,但是整理好思路就不難。
本質上,我們要找到當前刪除的節點的右子樹中的節點值最小的節點,也就是右邊第一個大於當前刪除節點的節點。我們用 s 來指向這個節點,後期我們將其作為代替當前刪除的節點。
但是,s 情況的不同也會導致一些處理上的區別。
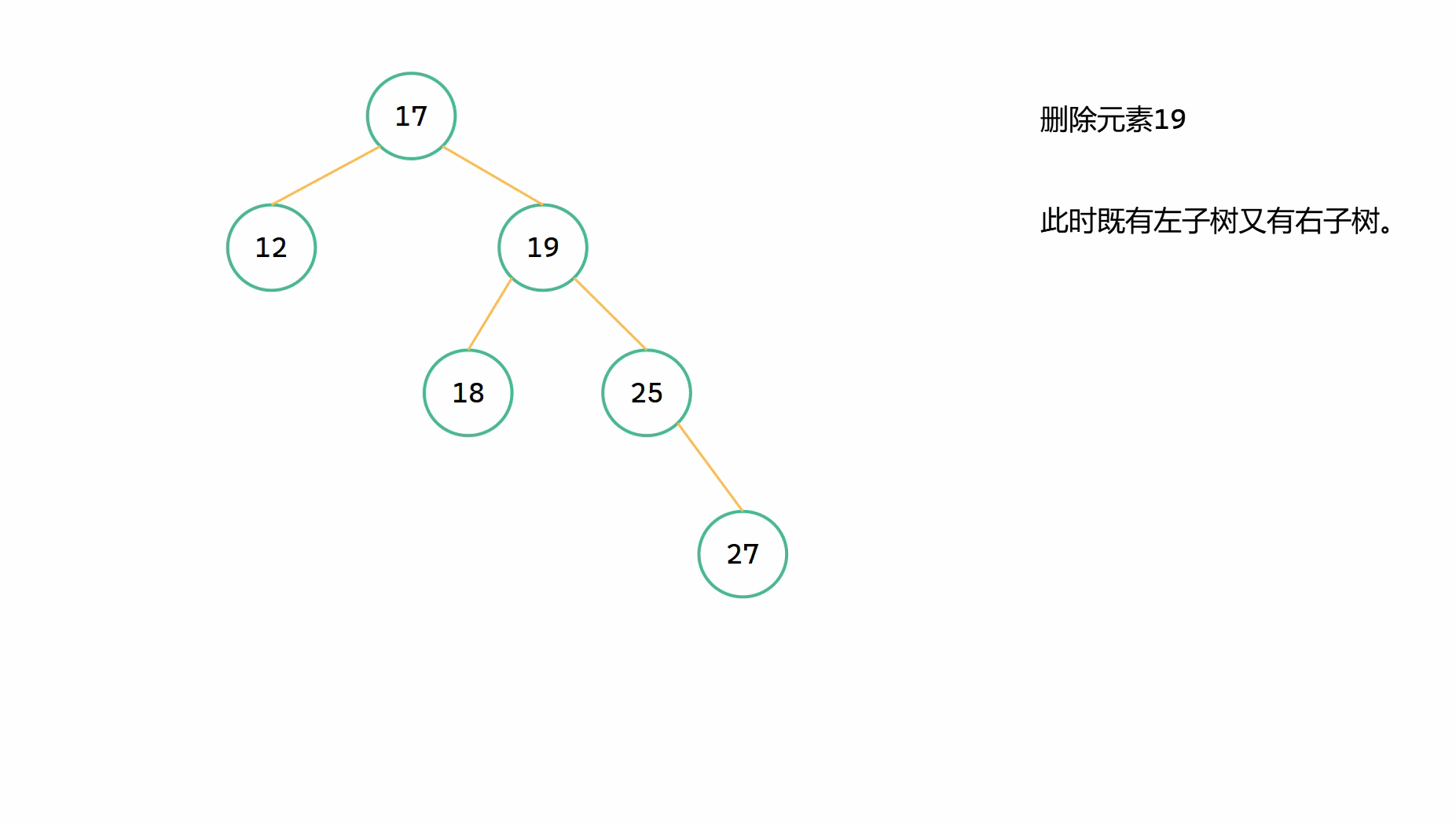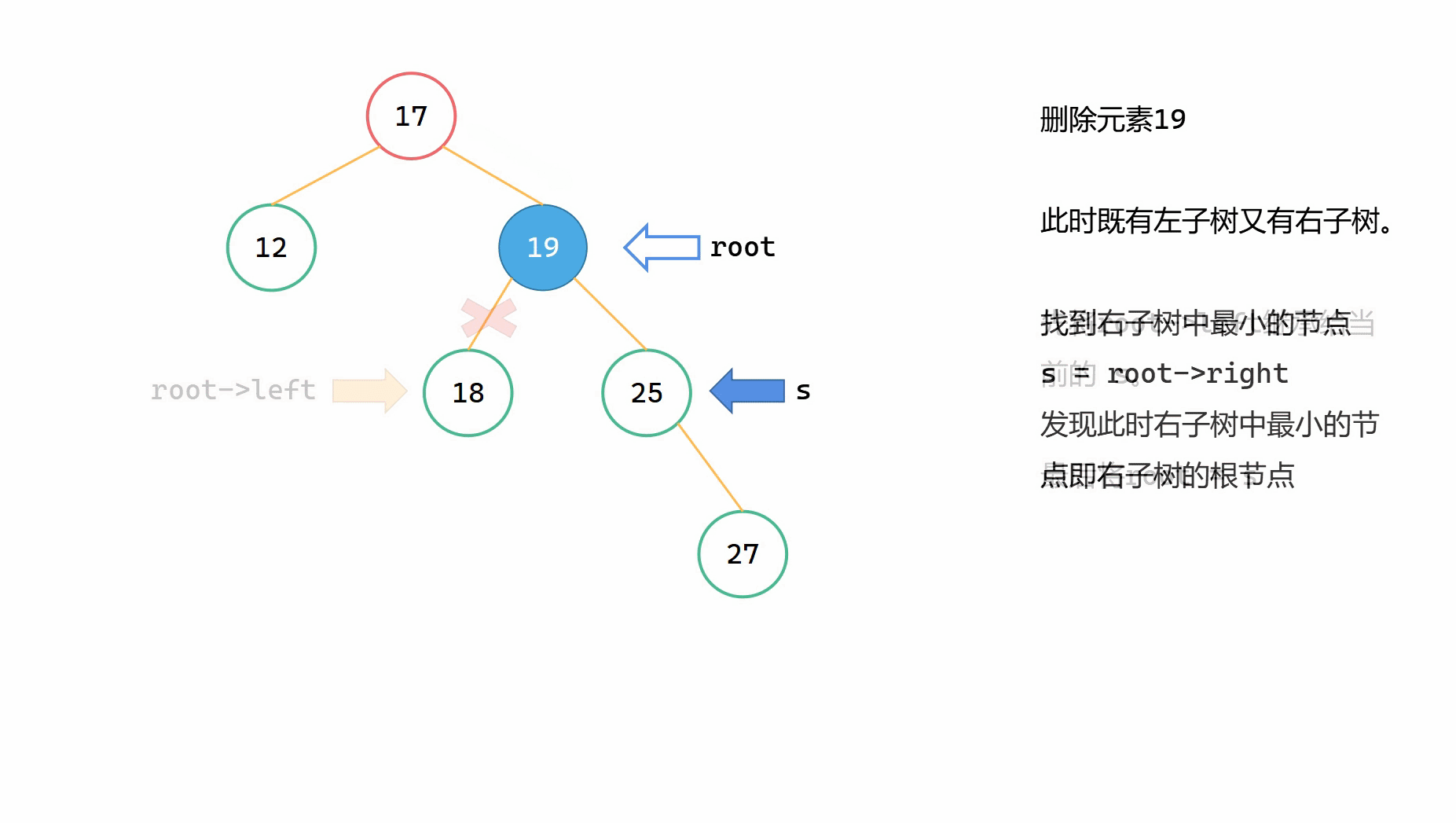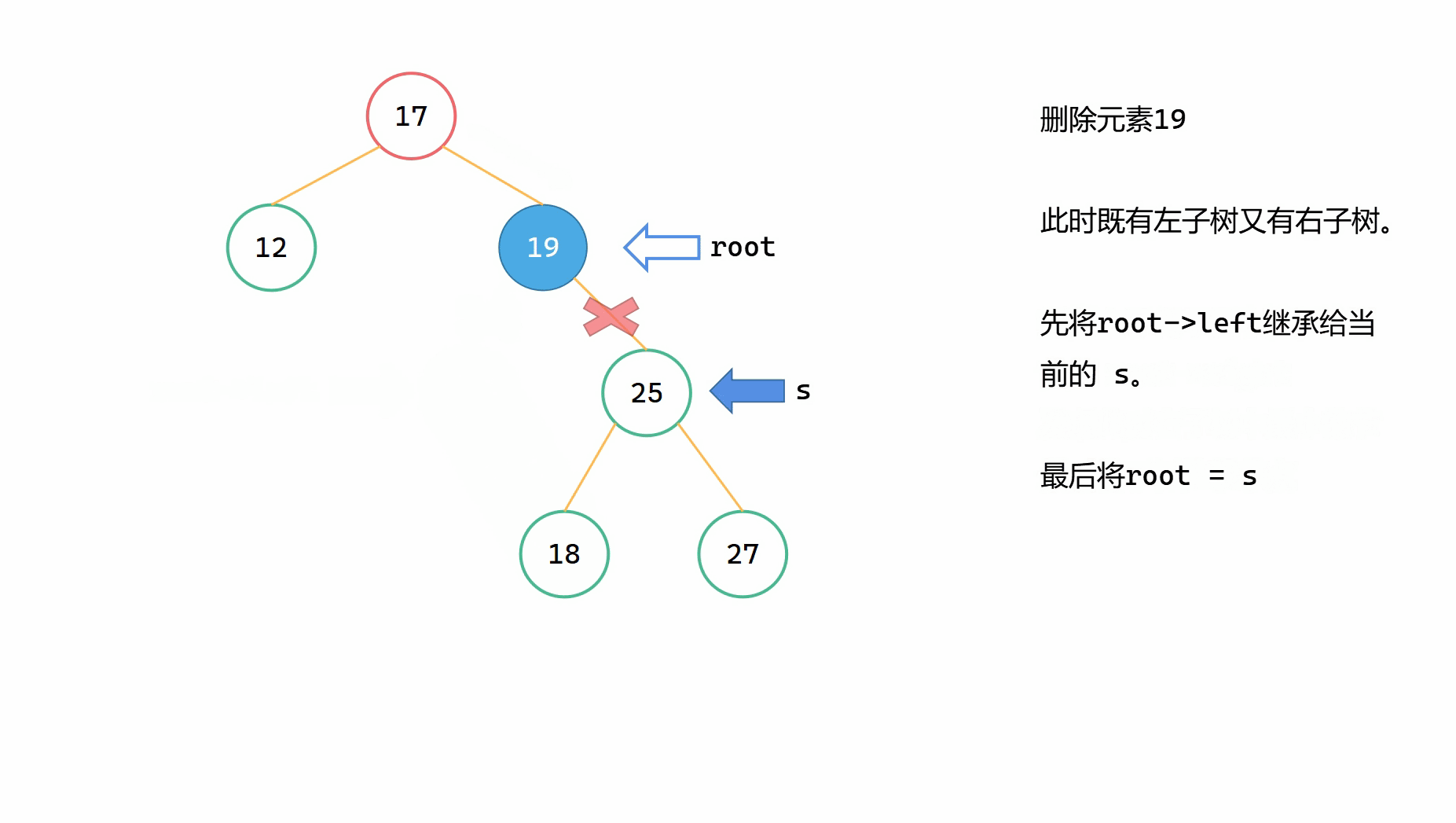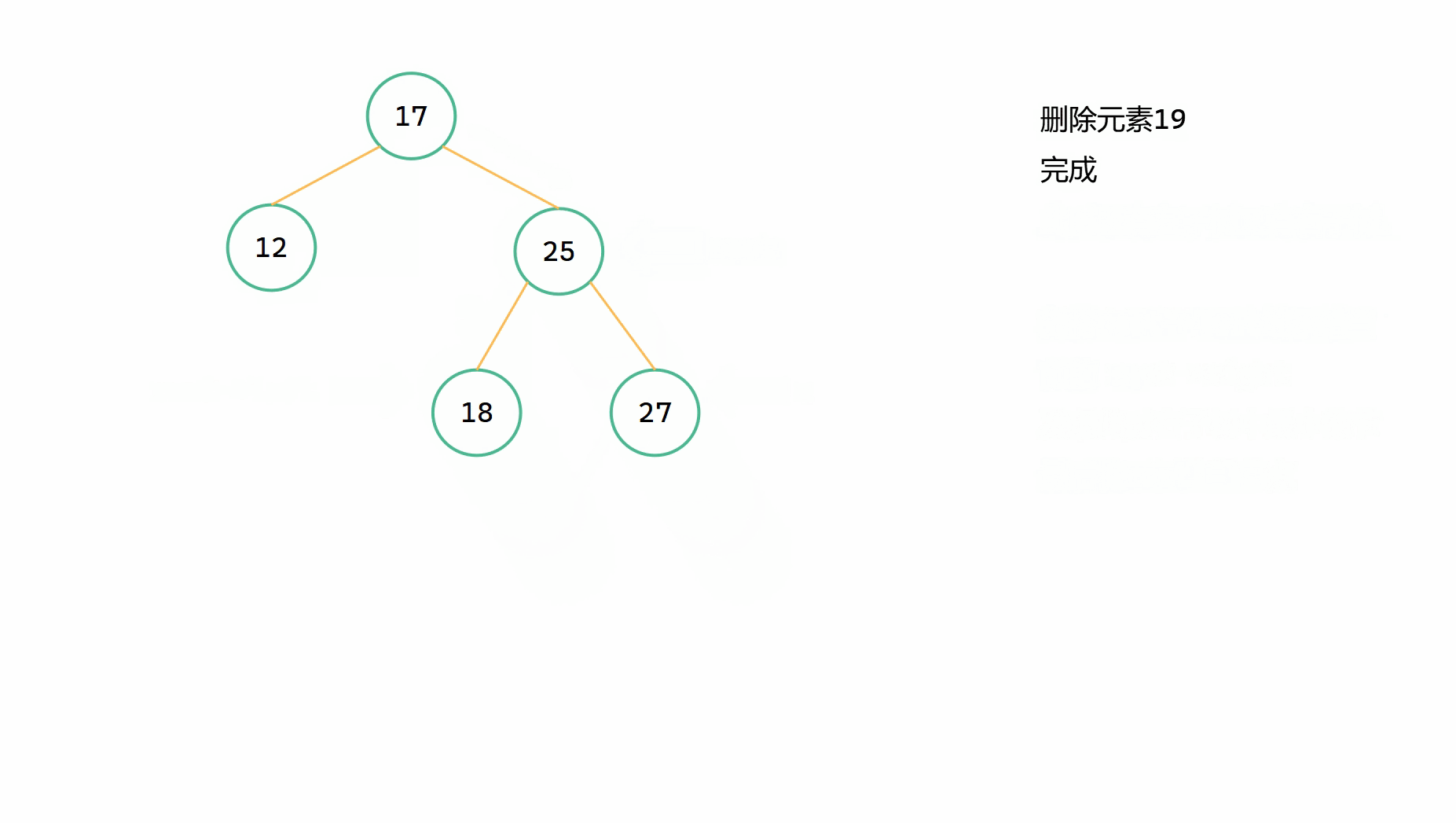
(1)右子樹根節點為右邊的最小節點
s 指向的是右子樹中的最小的節點,如果右子樹的左子樹為空,也就是說右子樹的根節點即右子樹中最小的節點。那麼此時 s 就指向這個右子樹根節點,然後只需要將刪除節點 root 的左子樹繼承給 s 的 left ,最後將 s 代替刪除節點 root 就可以了。這樣就可以保持二元搜尋樹的性質。
基本步驟
(1)此時 s 就指向 root->right ;
(2)將 root->left 繼承給 s->left ;
(3)s 代替刪除節點, root = s。
圖解
(2)最後一種情況
基本步驟
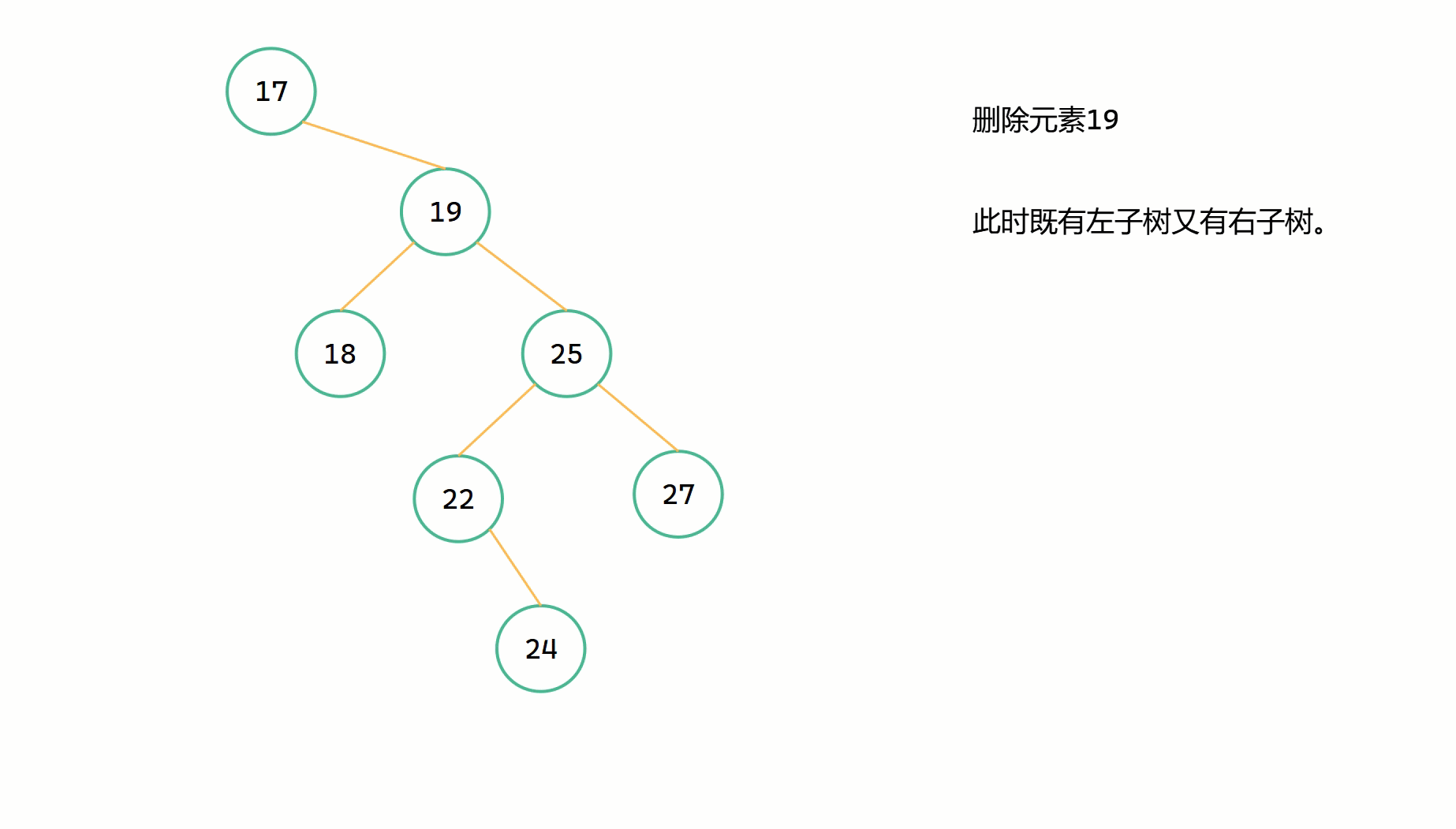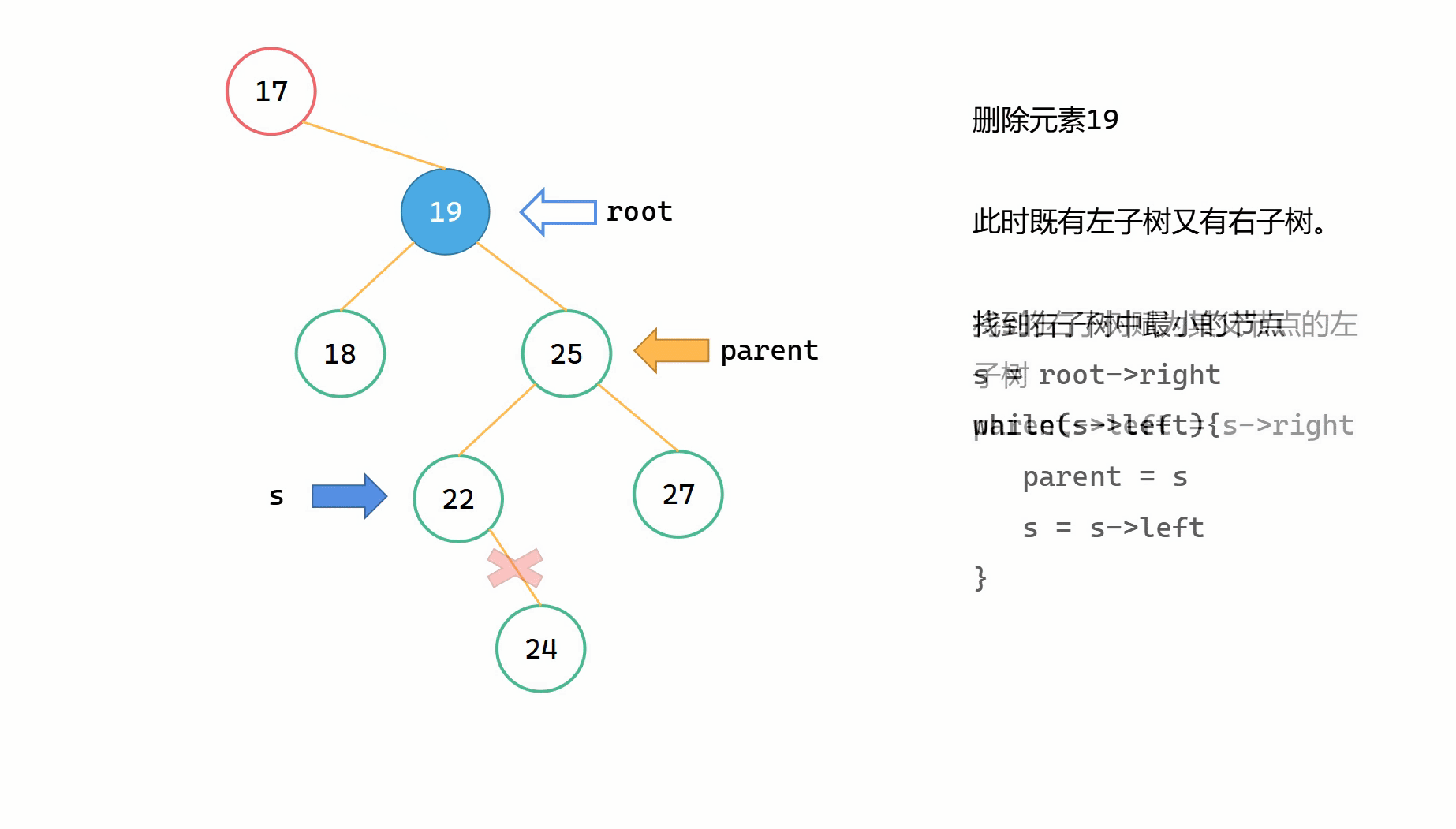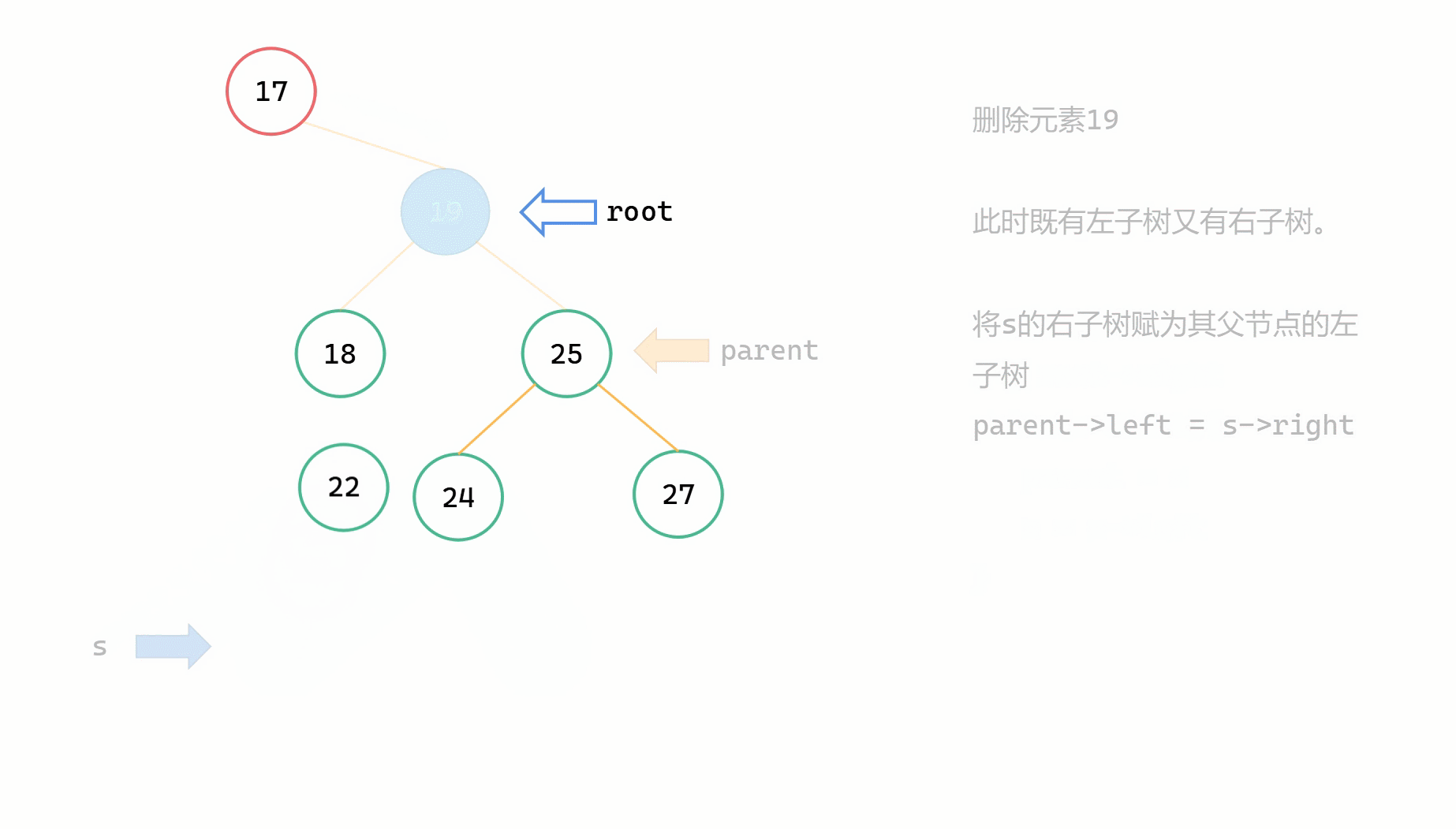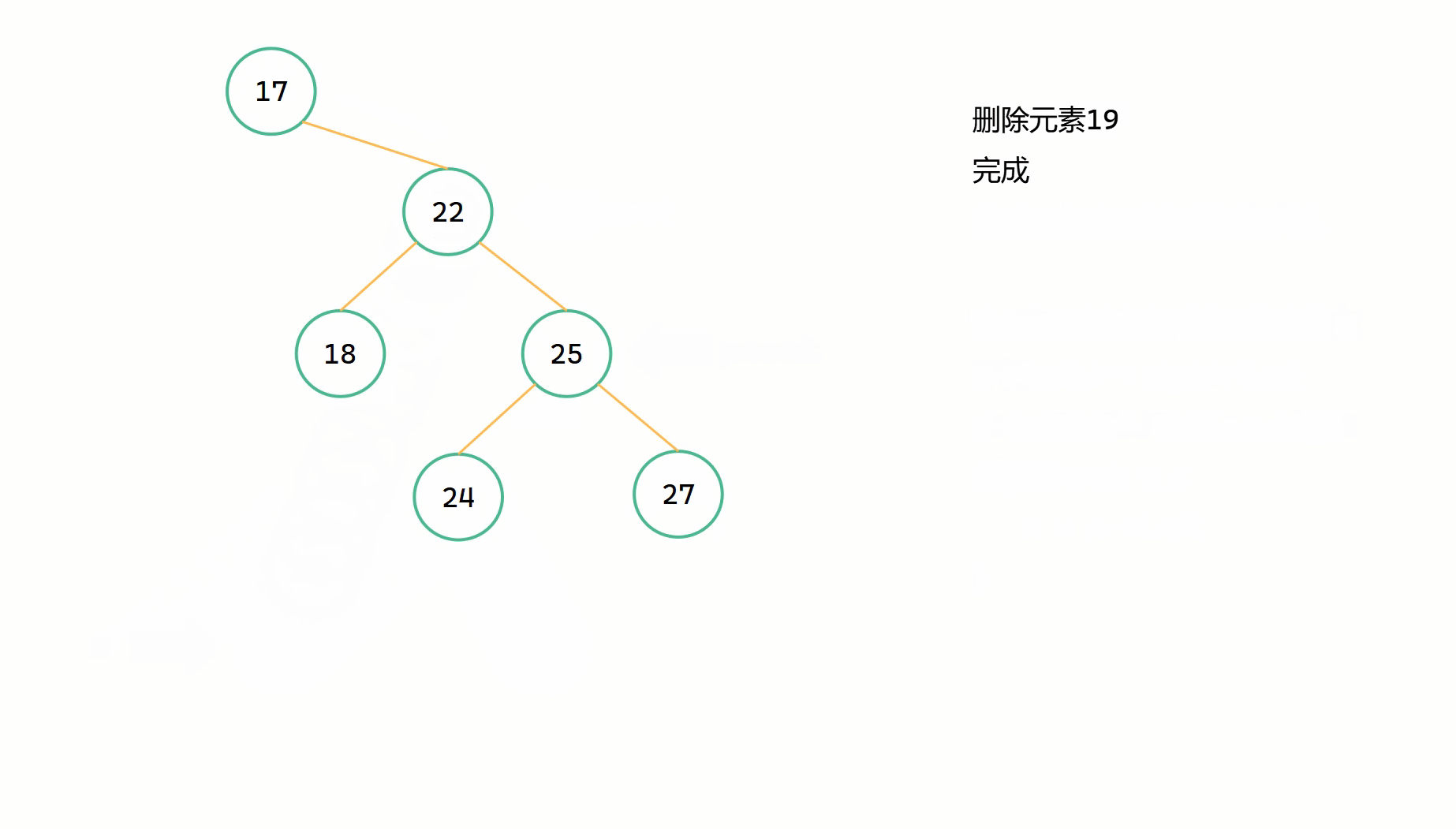
s 指向的是右子樹中的最小的節點,假如右子樹的左子樹不為空,那麼我們首先要先一直向左搜尋,直到右子樹的最左邊,即找到最左邊的節點。而且這個最左邊的節點一定是沒有左子樹的,但是可能存在右子樹。為了能夠順利的讓 s 代替刪除節點 root,根據 s 一定是其父節點的左子樹的特點,我們需要先將 s 的右子樹繼承給其父節點 parent,然後此時的 s 就形成一個單獨的節點。最後將刪除節點 root->left 賦給 s 的左子樹,將 root->right 賦給 s 的右子樹,將 root = s 完成代替操作。
為了將 s 的右子樹繼承給其父節點 parent,在右子樹中一直往左尋找最左邊的節點時,我們需要定義 parent 來記錄其父節點。
(1)在刪除節點 root 的右子樹中一直往左搜尋,找到最左邊的節點 s ;
(2)將 s 的右子樹繼承給 parent, parent->left = s->right ;
(3)將 root 的左右子樹繼承給 s, s->left = root->left, s->right = root->right ;
(4)最後 root = s 。
圖解
二元搜尋樹刪除程式碼
//二叉排序樹元素的刪除
void Delete_BST(BinaryTree &root, Elemtype val){
BinaryTree t = root, parent = NULL, s = NULL;
if(!t){ //要刪除節點不存在
puts("要刪除的節點不存在");
return;
}
//當前的root為要刪除的節點
if(t->val == val){
if(!t->leftchild && !t->rightchild){ //要刪除的節點是一個葉子結點 直接置NULL
root = NULL;
}
else if(!t->leftchild && t->rightchild){ //要刪除的節點只有右子樹,將其右子樹的根節點代替刪除節點
root = t->rightchild;
}
else if(t->leftchild && !t->rightchild){ //要刪除的節點只有左子樹,將其左子樹的根節點代替刪除節點
root = t->leftchild;
}
/* **個人認為最難的地方 採用迭代法** */
else{ //要刪除的節點既有左子樹,又有右子樹
s = t->rightchild; //記錄刪除節點的右子樹根節點
//找到右子樹中最小的節點
if(!s->leftchild){ //如果此時的s沒有左兒子,直接把刪除節點的左子樹變為此時s(刪除節點右兒子)的左子樹
s->leftchild = t->leftchild;
}else{
while(s->leftchild){ //找到刪除節點的右子樹中最左邊的節點s 即第一個大於刪除節點值的節點(後期將其代替刪除節點的位置)
parent = s; //記錄代替位置節點的父節點
s = s->leftchild;
}
parent->leftchild = s->rightchild;//若代替位置節點有右子樹,把其右子樹繼承給父節點(重構刪除節點的右子樹)
s->leftchild = t->leftchild; //刪除節點的左子樹變為代替節點的左子樹
s->rightchild = t->rightchild; //刪除節點的右子樹變為代替節點的右子樹
}
root = s; //最後將當前s代替要刪除的節點
}
free(t);
}
else if(val > t->val){
Delete_BST(t->rightchild, val); //向其右子樹尋找要刪除的節點
}
else if(val < t->val){
Delete_BST(t->leftchild, val); //向其左子樹尋找要刪除的節點
}
}
二元搜尋樹的平均查詢度
基本概念
ASL(Average Search Length),即平均查詢長度,在查詢運算中,由於所費時間在關鍵字的比較上,所以把平均需要和待查詢值比較的關鍵字次數稱為平均查詢長度。
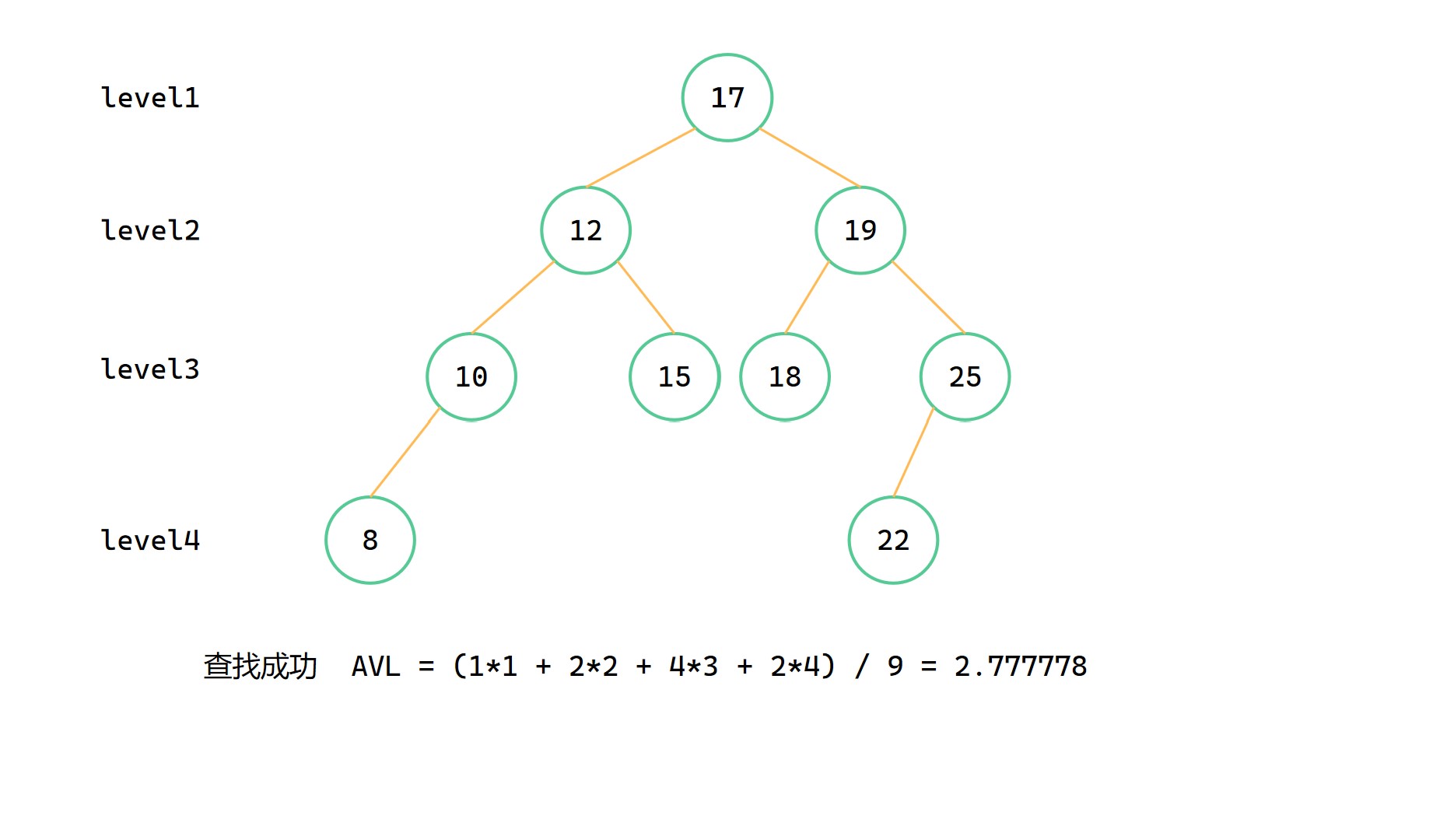
查詢成功情況下的AVL
計算公式
其中 i 表示當前層級,numi 表示第 i 層的節點個數,nodesum 表示整顆二元搜尋樹的節點個數。
圖解
計算二元樹節點個數程式碼
//計算二元樹節點的個數
int Nodenum_of_BST(BinaryTree root){
if(!root)
return 0;
return Nodenum_of_BST(root->leftchild) + Nodenum_of_BST(root->rightchild) + 1;
}
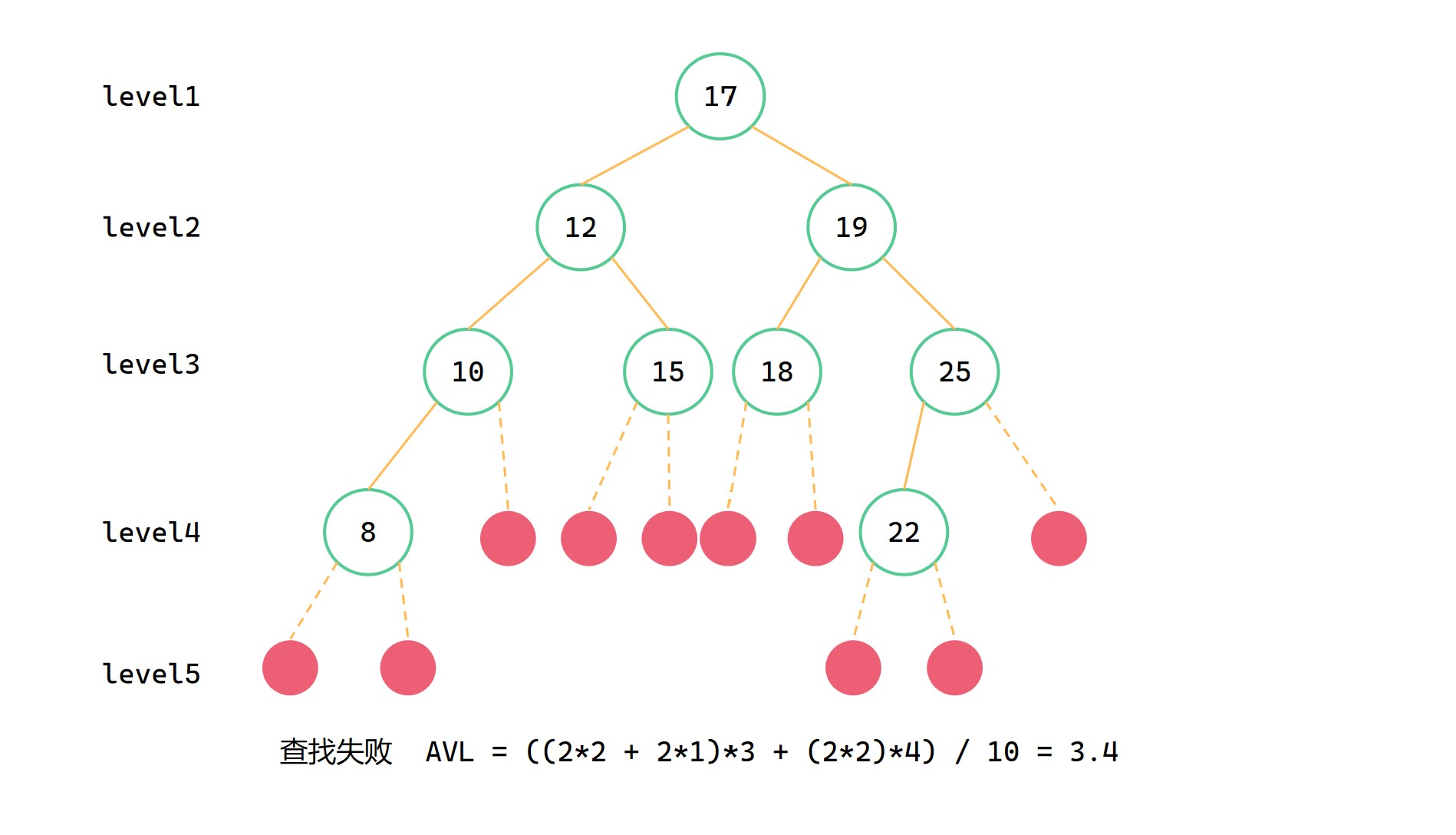
查詢失敗情況下的AVL
計算公式
其中 i 表示當前層級,supplei 表示第 i 層的要補全的節點個數,supplesum 表示整顆二元搜尋樹的要補全的總節點個數。
圖解
利用層次遍歷求補全節點
double sum1 = 0, sum2 = 0;
//全域性變數 sum1 = ∑(各層節點數 × 對應層級), sum2 = ∑(各層補全節點 × (對應層級-1))
int n0 = 0, n1 = 0;
//全域性變數 分別用於計算每一層葉子節點 和 度數為1的節點
int supplesum = 0;
//全域性變數 計算補全的節點總數
//層次遍歷 並利用佇列計算二元樹每一層的節點個數
void Show_Level_Order(BinaryTree root){
if(!root)
return;
BinaryTree t = NULL;
int level = 1;
std::queue<BinaryTree> q;
q.push(root);
while(!q.empty()){
n0 = n1 = 0;
int n = q.size();
for(int i = 0; i < n; i++){
t = q.front();
q.pop();
printf("%d ", t->val);
if(t->leftchild) q.push(t->leftchild);
if(t->rightchild) q.push(t->rightchild);
if(!t->leftchild && !t->rightchild)
n0 ++ ; //度數為0的節點
if(!t->leftchild && t->rightchild || t->leftchild && !t->rightchild)
n1 ++ ; //度數為1的節點
}
printf("\n");
sum1 += n * level; //每一層節點個數*層級
sum2 += (n0 * 2 + n1) * level; //每一層下方需補全節點*層級
supplesum += (n0 * 2 + n1); //補全的節點個數
level++;
}
}