遺傳演演算法求TSP問題
一、實驗內容及目的
本實驗以遺傳演演算法為研究物件,分析了遺傳演演算法的選擇、交叉、變異過程,採用遺傳演演算法設計並實現了商旅問題求解,解決了商旅問題求解最合適的路徑,達到用遺傳演演算法迭代求解的目的。選擇、交叉、變異各實現了兩種,如交叉有順序交叉和部分交叉。
二、實驗環境
Windows10
開發環境Python 3/Flask
三、實驗設計與實現
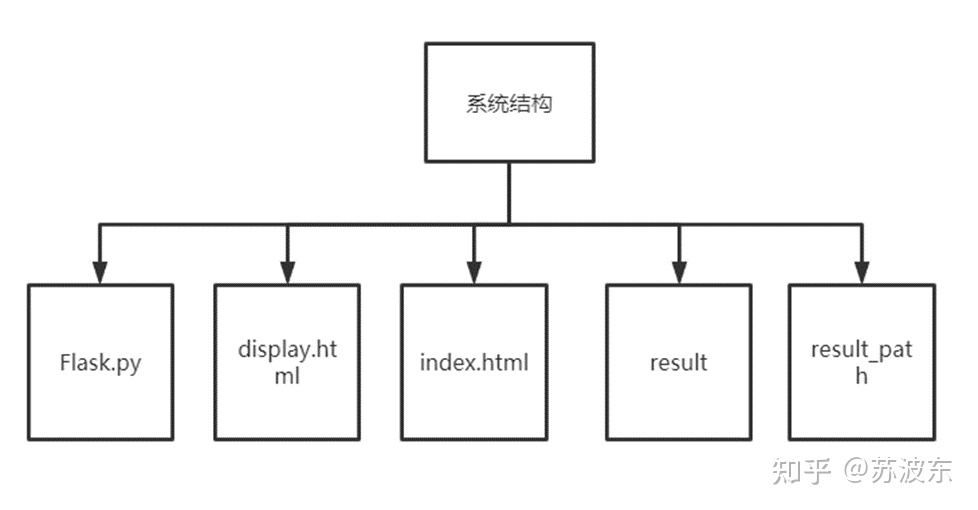
圖1軟體結構圖
Flask.py是後端核心程式碼,裡面是遺傳演演算法實現,index.html為首頁,即第一次進入網頁的頁面,進入之後可以進行引數設定,之後點選開始,引數會傳到Flask.py中進行解析和演演算法執行,最終將迭代結果存到result(儲存迭代結果圖)和result_path(儲存最短路徑圖)在返回給display.html頁面顯示。
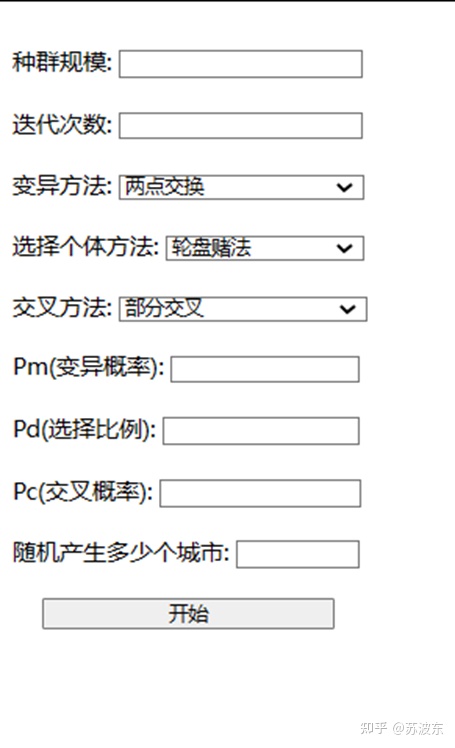
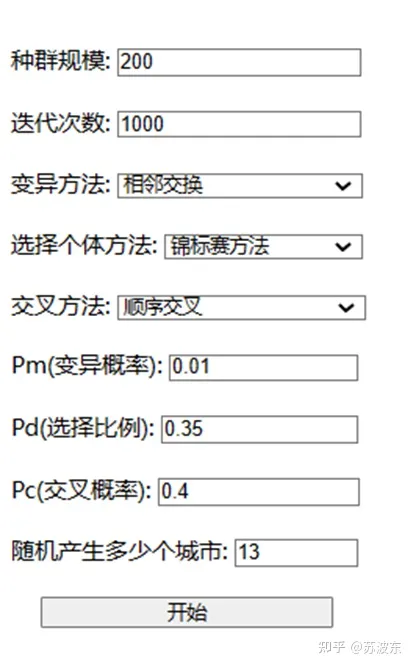
圖2系統介面圖
輸入種群規模、迭代次數、變異概率、選擇比例、交叉概率並選擇變異方法、選擇個體方法、交叉方法。點選開始即可執行該系統。
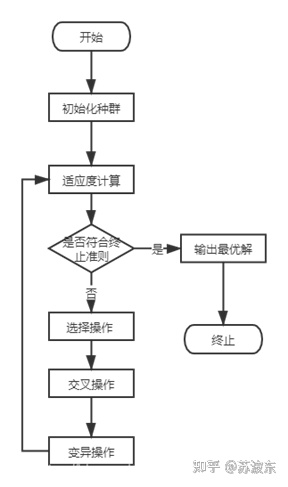
具體演演算法流程圖:

圖3核心演演算法流程圖
流程圖描述:首先根據引數城市數量和種群規模初始一個城市座標矩陣的列表並計算城市間的距離存到矩陣,最後生成一個路徑矩陣,這樣就可以進入下一步計算適應度,每一條路徑都有其路徑距離值和適應度,接下來一次進行選擇,交叉,變異操作,迴圈往復,直至達到了引數中的迭代次數限制。
選擇—輪盤賭:(這裡我的演演算法選出的種群數量不一定就恰好是根據比例算出的數量)
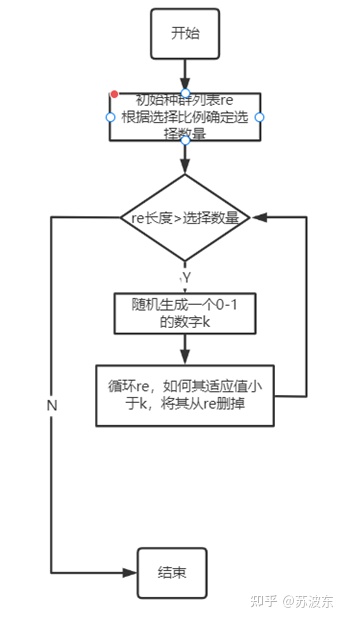
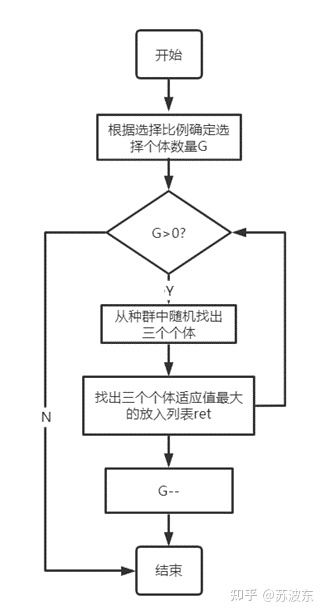
選擇—錦標賽:
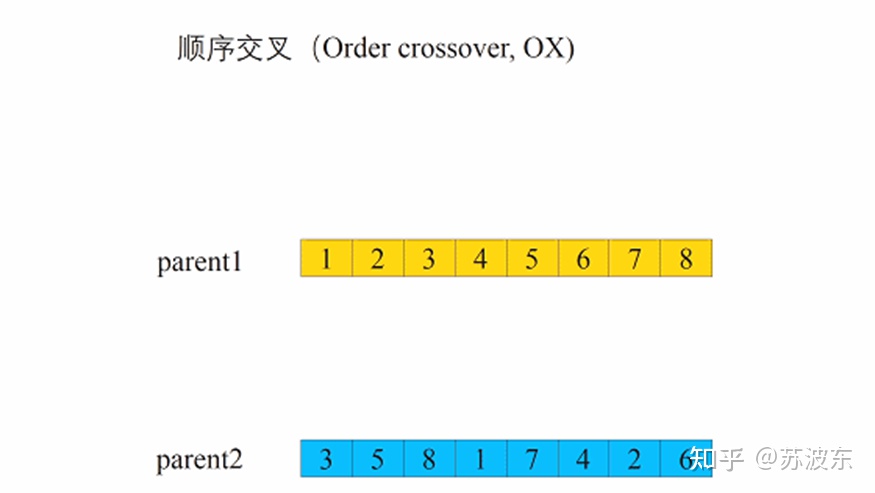
交叉—順序交叉:
1、 選切點X,Y
2、 交換中間部分
3、 從第二個切點Y後第一個基因起列出原順序,去掉已有基因
4、 從第二個切點Y後第一個位置起,將獲得的無重複順序填入
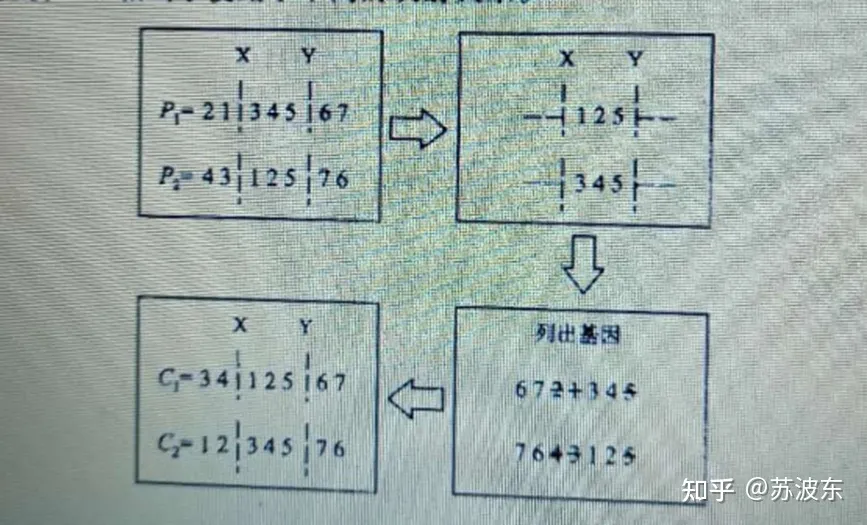
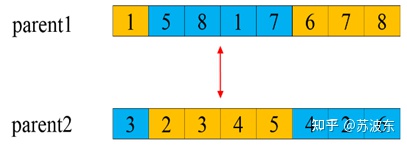
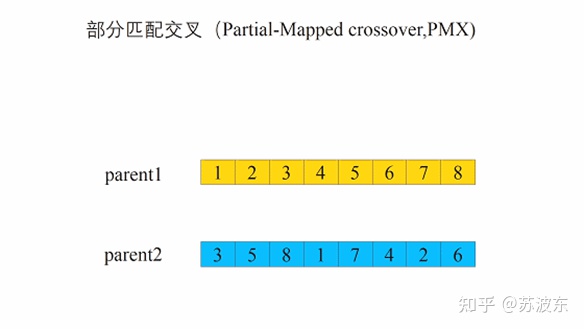
交叉—部分交叉:
1、 選切點oop
2、 選取oop到oop+3部分交換(我這裡就是三個,你可以做成隨機的幾個)
3、 判斷是否有重複的,若重複則進行對映,保證形成的新一對子代基因無衝突。
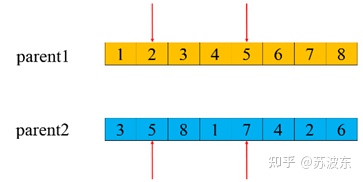
變異—兩點交換
1、 隨機選取兩點
2、 兩點進行交換
變異—相鄰交換
1、 隨機選取一點
2、 和該點的後面點進行交換
適應度函數:經過測試得A取5,B取0效果好,所以實驗中直接取了A=5,B=0執行
借鑑了sigmoid函數的形式,並對資料做了最大最小標準化,A、B是人為給定的常係數mean、max、min是種群所有個體的目標函數值的均值、最大值、最小值影象如下A=5,B=0
適應值較大的更容易進入下一代種群中
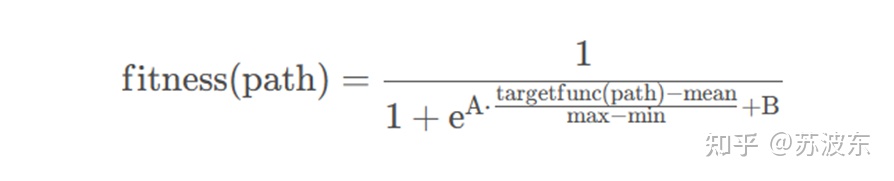
四、實驗結果與測試
表1 遺傳演演算法解決TSP問題的測試用例
| 測試內容 | 測試用例 | 預期結果 | 實際結果 |
| 種群規模 | 1.不輸入 2.輸入除數位其他 3.輸入整數數位 4.輸入小數或者負數 |
失敗 失敗 成功 失敗 |
與預期相同 |
| 迭代次數 | 5.不輸入 6.輸入除數位其他 7.輸入整數數位 8.輸入小數或者負數 |
失敗 失敗 成功 失敗 |
與預期相同 |
| 變異方法 | 9.選擇兩點交換 10.選擇相鄰交換 |
成功 成功 |
與預期相同 |
| 選擇個體方法 | 11.選擇輪盤賭 12.選擇錦標賽 |
成功 成功 |
與預期相同 |
| 交叉方法 | 13.選擇部分交叉 14.選擇順序交叉 |
成功 成功 |
與預期相同 |
| 變異概率 | 15.不輸入 16.輸入除數位其他 17.輸入小於1的小數 18.輸入非小於1的小數或者整數 |
失敗 失敗 成功 失敗 |
與預期相同 |
| 選擇比例 | 19.不輸入 20.輸入除數位其他 21.輸入小於1的小數 22.輸入非小於1的小數或者整數 |
失敗 失敗 成功 失敗 |
與預期相同 |
| 交叉概率 | 23.不輸入 24.輸入除數位其他 25.輸入小於1的小數 26.輸入非小於1的小數或者整數 |
失敗 失敗 成功 失敗 |
與預期相同 |
| 隨機產生多少個城市 | 27.不輸入 28.輸入除數位其他 29.輸入整數數位 30. 輸入小數或者負數 |
失敗 失敗 成功 失敗 |
與預期相同 |
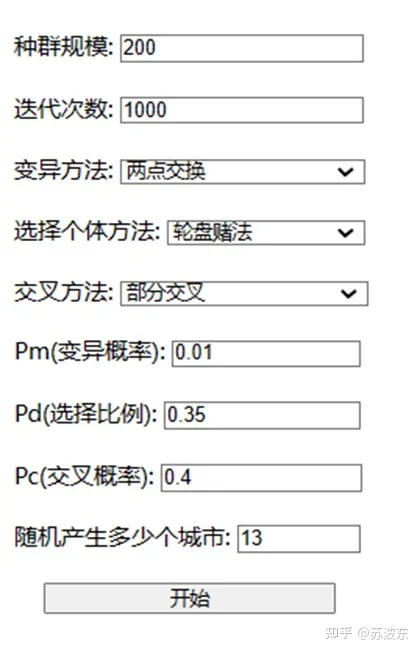
在上述引數設定好之後,即可開始執行系統,最後產生如圖11的迭代結果圖,最上面是自己的引數設定和最後生成的最小路徑min_dist,圖示整體為每次迭代的路徑距離,可見隨著迭代次數增加,路徑距離一直減小最後趨於穩定。圖12為用python畫的路徑圖,圖中橫軸縱軸為城市位置的X,Y座標。
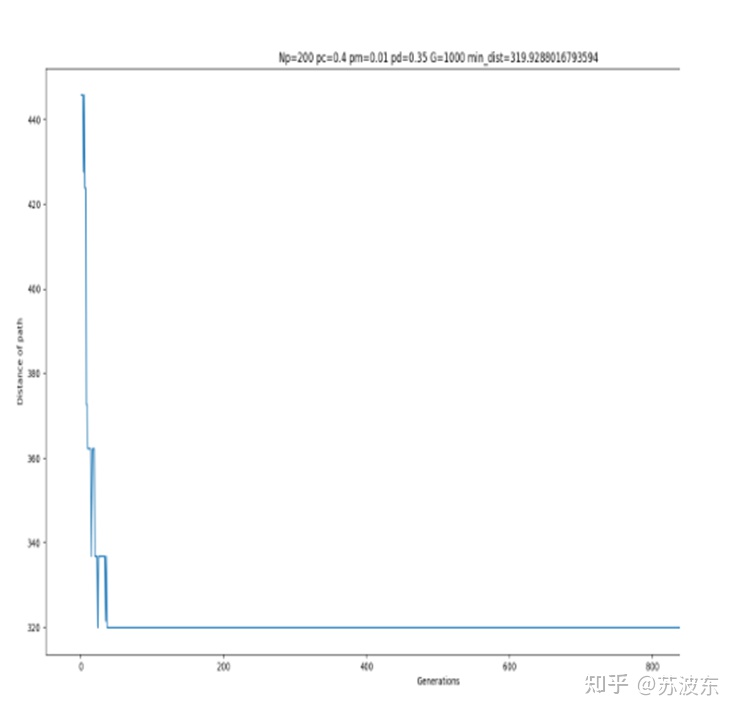
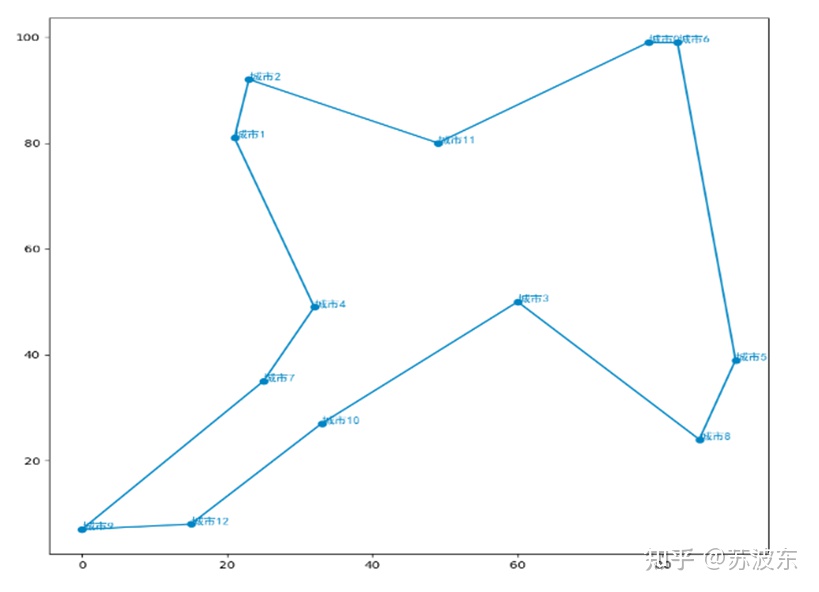
接下來重新選擇其他引數來執行一下,看一下有沒有區別。
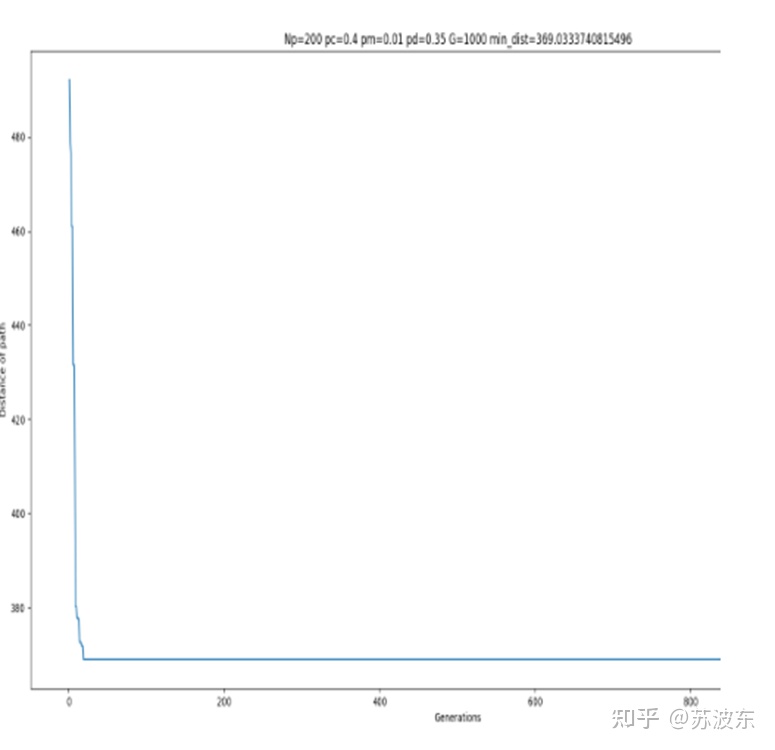
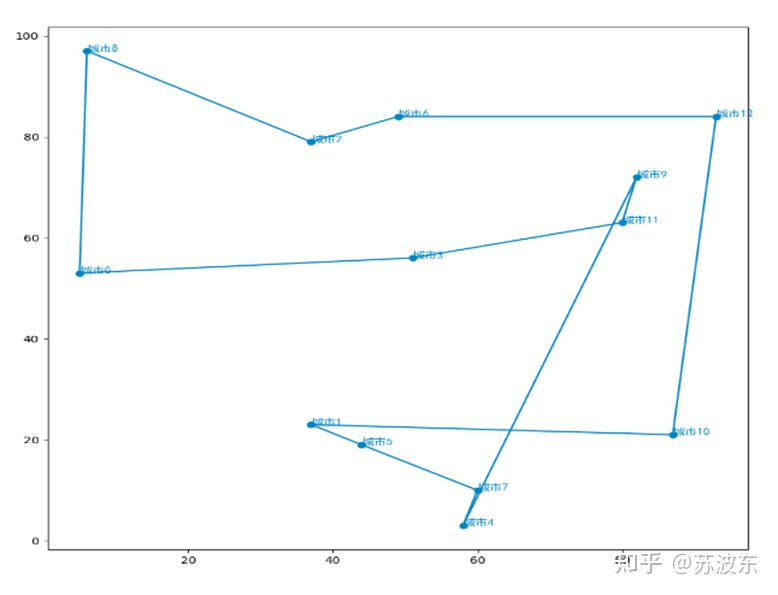
可以從迭代影象看出,引數不同會導致迭代中結果的不同,第一次引數設定的迭代中在前段迭代不穩定,忽上忽下,之後穩定,而第二次引數設定後迭代很快就穩定,沒有忽上忽下的現象,所以不同的選擇、變異、交叉方法會使迭代結果不同。所以可以根據隨機設定讓計算機找到最合適的引數設定。
歡迎關注我的知乎平臺,我將持續為您解答一系列問題!