圖解B樹及C#實現(3)資料的刪除
前言
本文為系列文章
- B樹的定義及資料的插入
- 資料的讀取及遍歷
- 資料的刪除
閱讀本文前,建議先複習前兩篇文章,以便更好的理解本文。
從刪除的資料所在的節點可分為兩種情況:
- 從葉子節點刪除資料
- 從非葉子節點刪除資料
無論從葉子節點還是非葉子節點刪除資料時都需要保證B樹的特性:非根節點每個節點的 key 數量都在 [t-1, 2t-1] 之間。
藉此保證B樹的平衡性。
之前介紹的插入資料關注的是這個範圍的上限 2t-1,插入時,如果節點的 key 數量大於 2t-1,就需要進行資料的分裂。
而刪除資料則關注是下限 t-1,如果節點的 key 數量小於 t-1,就需要進行資料的移動或者合併。
刪除資料時,需要考慮的情況比較多,本文會分別討論這些情況,但一些比較邊緣的情況為避免描述過於複雜,不再文中討論,而是在程式碼中進行了註釋。
因為刪除邏輯比較複雜,請結合完整程式碼進行閱讀。
https://github.com/eventhorizon-cli/EventHorizon.BTree/blob/b51881719146a86568669cdc78f8524299bee33d/src/EventHorizon.BTree/BTree.cs
從葉子節點刪除資料
如果待刪除的資料在葉子節點,且該節點的 Item 數量大於 t-1,那麼直接刪除該資料即可。
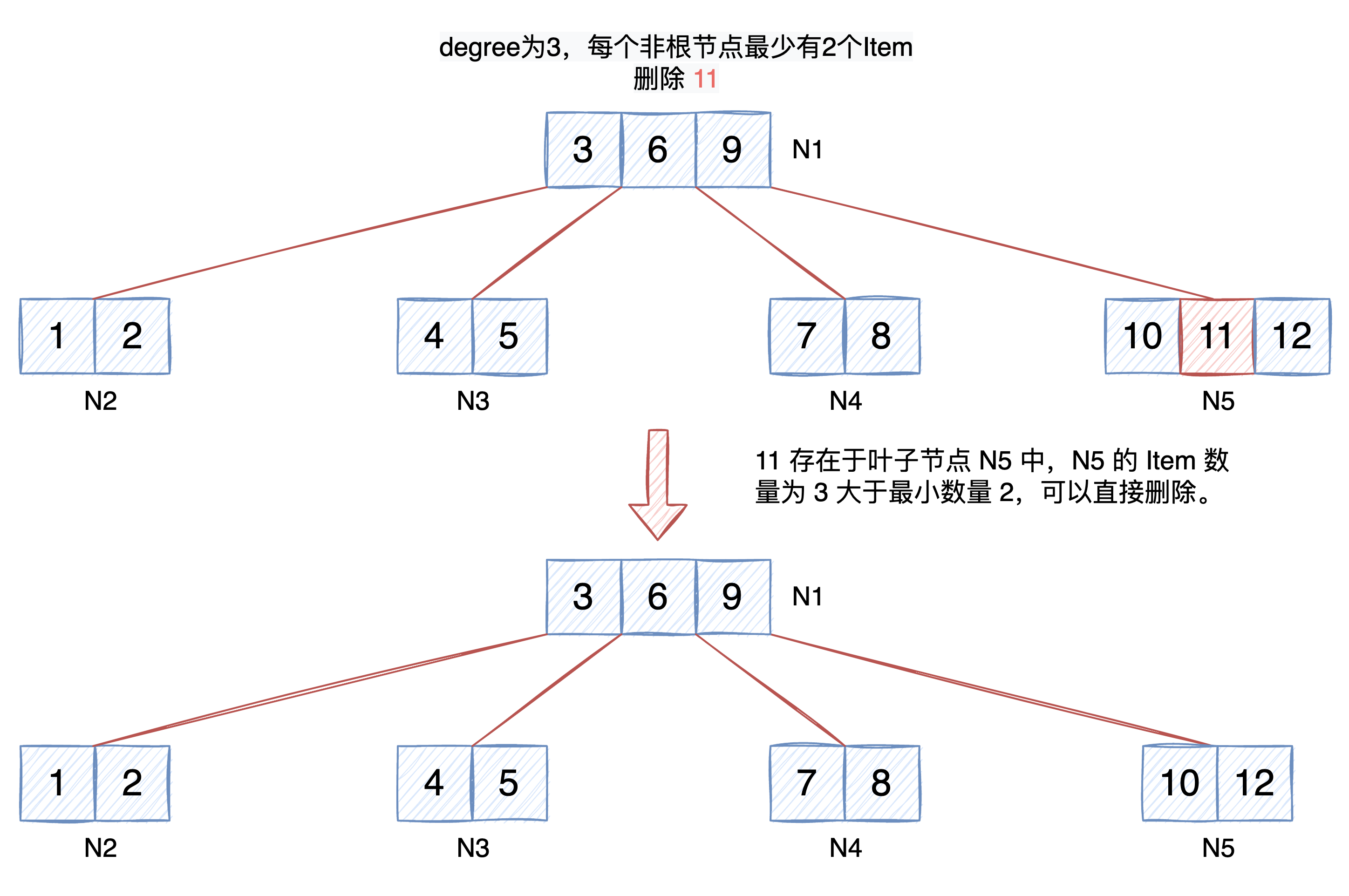
從非葉子節點刪除資料
如果待刪除的資料在非葉子節點,那麼需要先找到該資料的左子節點,然後將左子節點的資料替換到待刪除的資料,最後再刪除左子節點的資料。
這樣能保證被刪除資料的節點的 Item 數量不變,保證 B樹 有 k 個子節點的非葉子節點擁有 k − 1 個鍵的特性不受破壞。
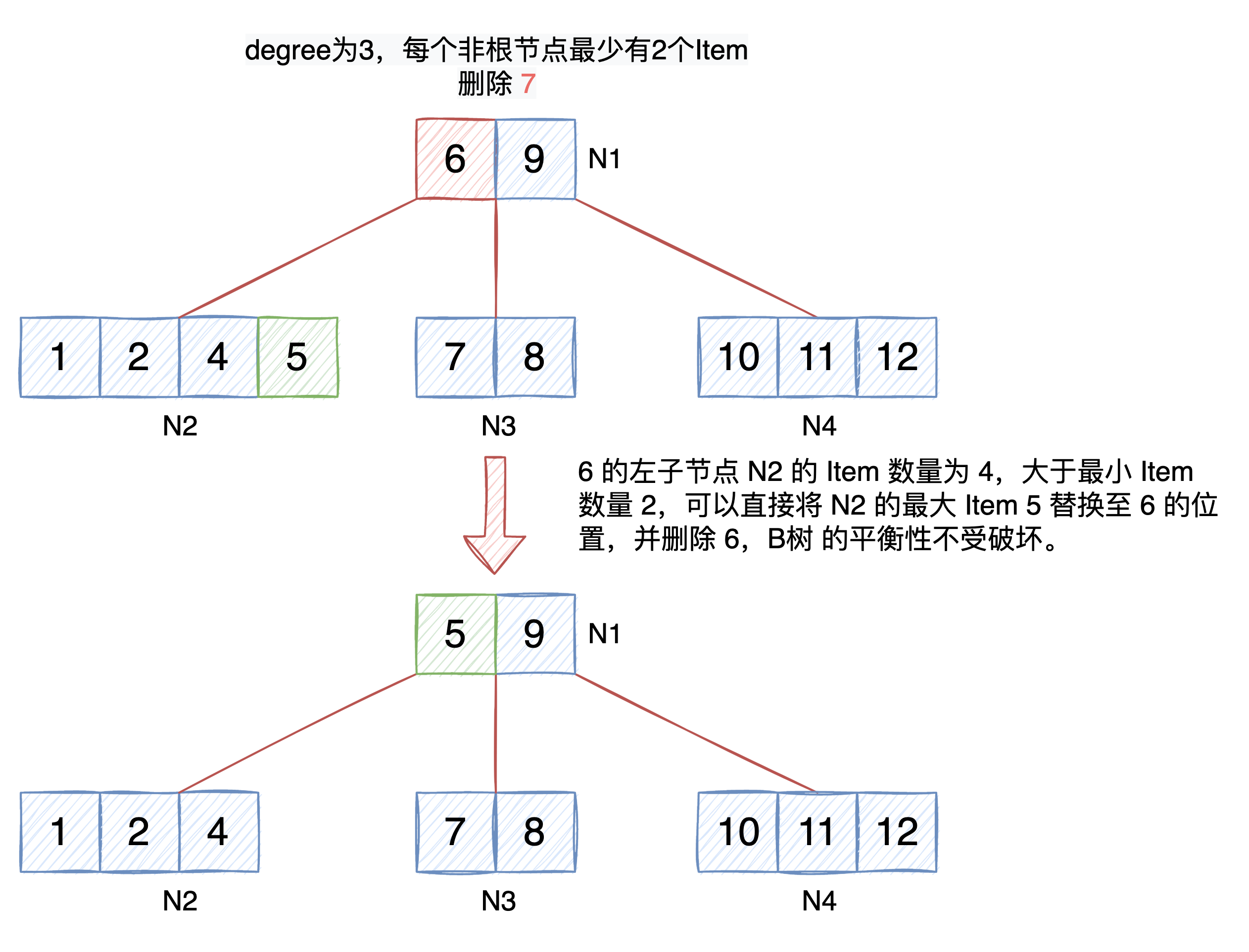
提前擴充只有 t-1 的 Item 的節點:維持 B樹 平衡的核心演演算法
在資料插入的時候,為了避免回溯性的節點分裂,我們提前將已滿的子節點進行分裂。
同樣的在資料刪除,不斷往下遞迴查詢時,如果遇到只有 t-1 個 Item 的節點,我們也需要提前將其擴充,以避免回溯性的節點處理。
擴充的節點不一定是最後資料所在的節點,只是向下查詢過程中遇到的節點。
節點擴充的分為兩類,一個是從兄弟節點借用 Item,一個是合併兄弟節點,被借用的兄弟節點需要滿足 Item 數量大於 t-1。具體可分為以下三種情況:
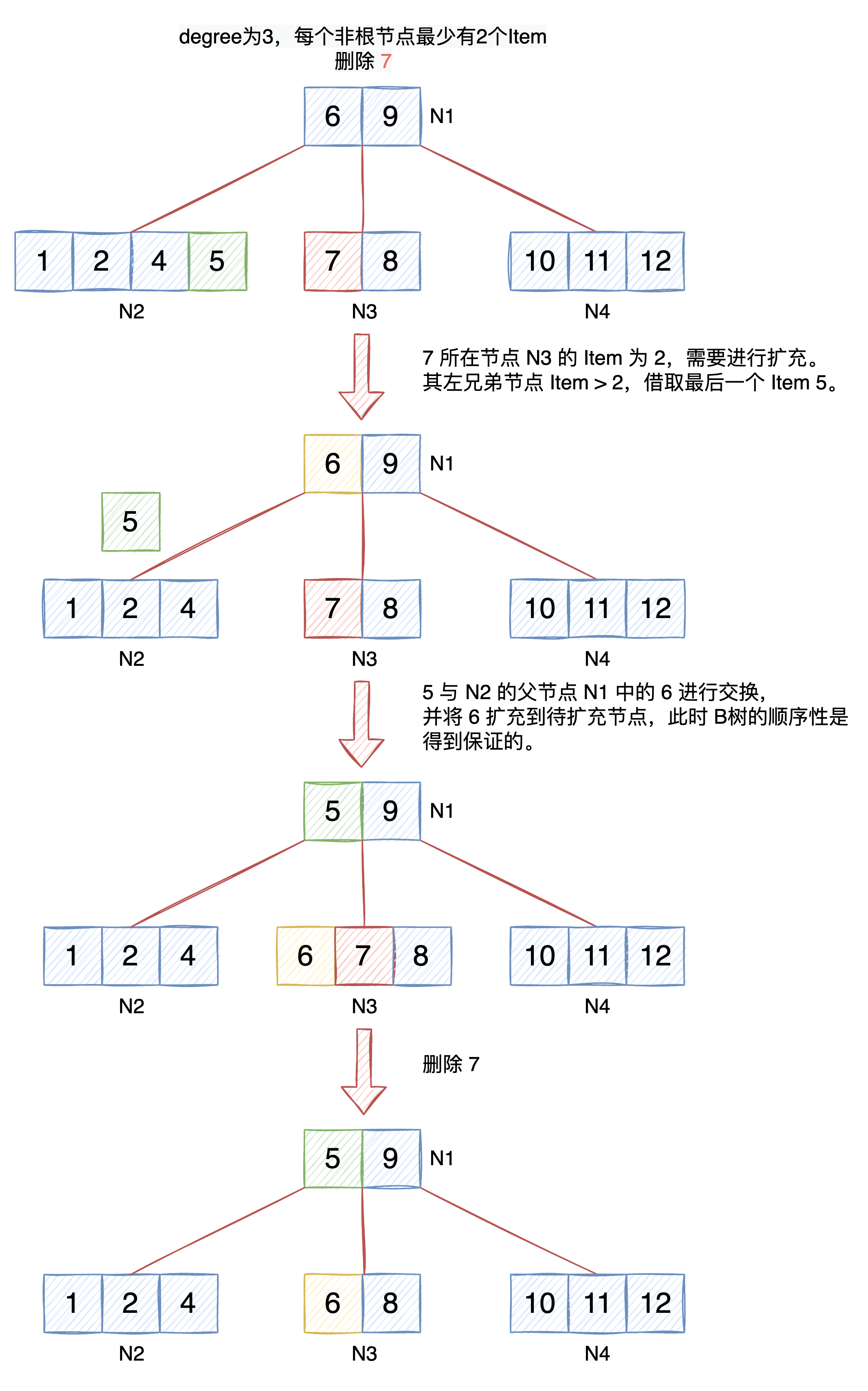
從左兄弟節點借用 Item
待擴充節點的左兄弟節點存在且左兄弟節點的 Item 數量 > t-1 時,從左兄弟節點借用 Item 進行擴充。
為了保證 B樹 資料的順序特性:任意 Item 的左子樹中的 Key 均小於該 Item 的 Key,右子樹中的 Key 均大於該 Item 的 Key。需要交換左兄弟節點的最右邊的 Item 和父節點中對應位置的 Item(位於左兄弟節點右側)。
以下圖為例進行說明:
從右兄弟節點借用 Item
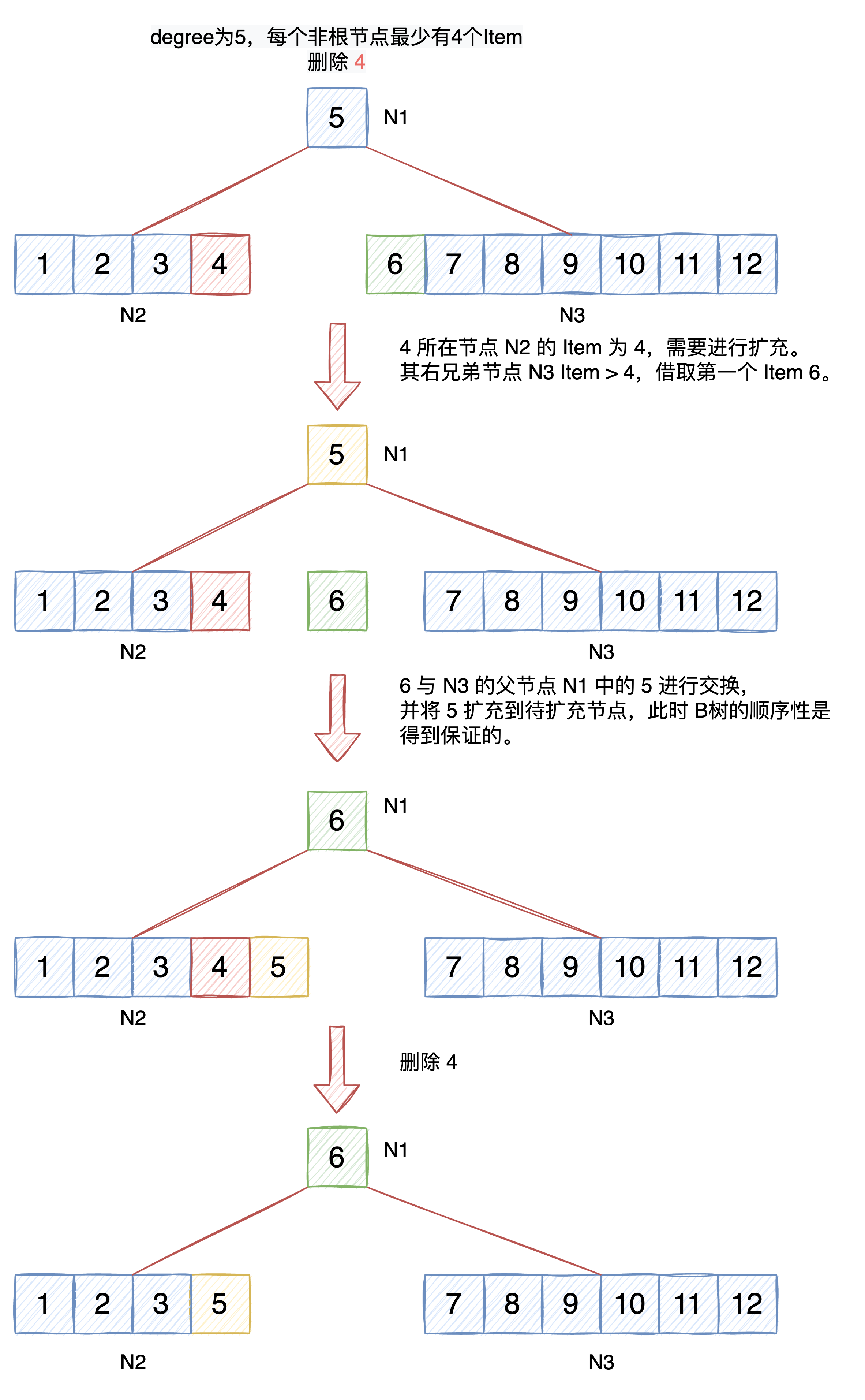
待擴充節點的左兄弟節點不存在或者左兄弟節點的 Item 數量 只有 t-1 時,無法外借。但右兄弟節點存在且右兄弟節點的 Item 數量 > t-1 時,從右兄弟節點借用 Item 進行擴充。
以下圖為例進行說明:
從兄弟節點進行擴充可以概括為:借用,交換,插入。
與左兄弟節點或者右兄弟節點合併
如果待擴充節點的左兄弟節點和右兄弟節點都不存在或者都只有 t-1 個 Item 時,無法外借。此時需要與左兄弟節點或者右兄弟節點進行合併。
以下圖為例進行說明:
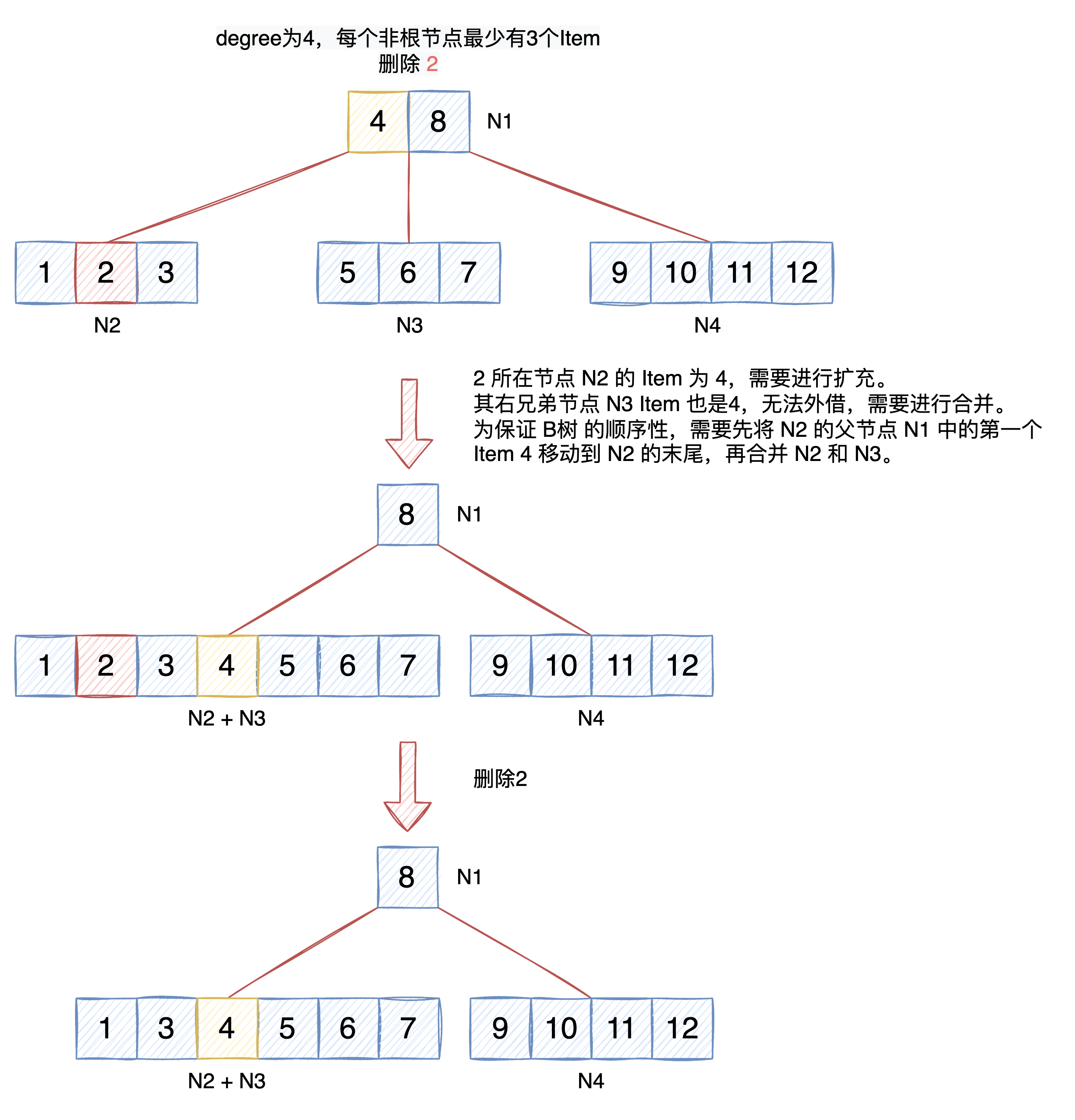
最值的刪除
之前章節介紹過 B樹 最值的查詢:
- 最小值:從根節點開始,一直往左子樹走,直到葉子節點。
- 最大值:從根節點開始,一直往右子樹走,直到葉子節點。
最值的刪除就是先找到最值的位置並將其刪除,在向下尋找的過程中,需要和普通的資料刪除一樣,對節點進行擴充或者合併。
程式碼實現
最值刪除是刪除的特殊情況,我們定義一個列舉用來區分普通資料的刪除,最小值的刪除以及最大值的刪除,這三種方式只在資料查詢的時候有所區分,其他的邏輯都是一樣的。
internal enum RemoveType
{
Item,
Min,
Max
}
public sealed class BTree<TKey, TValue> : IEnumerable<KeyValuePair<TKey, TValue?>>
{
public bool TryRemove([NotNull] TKey key, out TValue? value)
{
ArgumentNullException.ThrowIfNull(key);
return TryRemove(key, RemoveType.Item, out value);
}
public bool TryRemoveMax(out TValue? value) => TryRemove(default, RemoveType.Max, out value);
public bool TryRemoveMin(out TValue? value) => TryRemove(default, RemoveType.Min, out value);
private bool TryRemove(TKey? key, RemoveType removeType, out TValue? value)
{
if (_root == null || _root.IsItemsEmpty)
{
value = default;
return false;
}
bool removed = _root.TryRemove(key, removeType, out var item);
if (_root.IsItemsEmpty && !_root.IsLeaf)
{
// 根節點原來的兩個子節點進行了合併,根節點唯一的元素被移動到了子節點中,需要將合併後的子節點設定為新的根節點
_root = _root.GetChild(0);
}
if (removed)
{
_count--;
value = item!.Value;
return true;
}
value = default;
return removed;
}
}
主要的邏輯定義在 Node 中,不斷向下遞迴
internal class Node<TKey, TValue>
{
public bool TryRemove(TKey? key, RemoveType removeType, [MaybeNullWhen(false)] out Item<TKey, TValue?> item)
{
int index = 0;
bool found = false;
if (removeType == RemoveType.Max)
{
if (IsLeaf)
{
if (_items.Count == 0)
{
item = default;
return false;
}
// 如果是葉子節點,直接刪除最後一個元素,就是刪除最大的 Item
item = _items.RemoveLast();
return true;
}
// 當前節點不是葉子節點,需要找到最大的子節點,繼續向下查詢並刪除
index = ItemsCount;
}
if (removeType == RemoveType.Min)
{
if (IsLeaf)
{
if (_items.Count == 0)
{
item = default;
return false;
}
// 當前節點是葉子節點,直接刪除第一個元素,就是刪除最小的 Item
item = _items.RemoveAt(0);
return true;
}
// 當前節點不是葉子節點,需要找到最小的子節點,繼續向下查詢並刪除
index = 0;
}
if (removeType == RemoveType.Item)
{
// 如果沒有找到,index 表示的是 key 可能在的子樹的索引
found = _items.TryFindKey(key!, out index);
if (IsLeaf)
{
// 如果是葉子節點,能找到就刪除,找不到就返回 false,表示刪除失敗
if (found)
{
item = _items.RemoveAt(index);
return true;
}
item = default;
return false;
}
}
// 如果當前節點的左子節點的 Item 個數小於最小 Item 個數,就需要進行合併或者借元素
// 這個處理對應兩種情況:
// 1. 要刪除的 Item 不在當前節點的子節點中,為避免刪除後導致資料所在節點的 Item 個數小於最小 Item 個數,需要先進行合併或者借元素。
// 2. 要刪除的 Item 就在當前節點中,為避免刪除後導致當前節點的 Item 個數小於最小 Item 個數,需要先從左子節點中借一個 Item 過來,保證當前節點的 Item 數量不變。
// 為此先要保證左子節點被借用後的 Item 個數不小於最小 Item 個數。
if (_children[index].ItemsCount <= _minItems)
{
return GrowChildrenAndTryRemove(index, key!, removeType, out item);
}
var child = _children[index];
if (found)
{
// 如果在當前節點找到了,就刪除當前節點的 Item,然後將 左子節點 中的最大的 Item 移動到當前節點中
// 以維持當前節點的 Item 個數不變,保證 B樹 有 k 個子節點的非葉子節點擁有 k − 1 個鍵的特性。
item = _items[index];
child.TryRemove(default!, RemoveType.Max, out var stolenItem);
_items[index] = stolenItem;
return true;
}
return child.TryRemove(key!, removeType, out item);
}
private bool GrowChildrenAndTryRemove(
int childIndex,
TKey key,
RemoveType removeType,
[MaybeNullWhen(false)] out Item<TKey, TValue?> item)
{
if (childIndex > 0 && _children[childIndex - 1].ItemsCount > _minItems)
{
// 如果左邊的子節點存在且左邊的子節點的item數量大於最小值,則從左邊的子節點借一個item
var child = _children[childIndex];
var leftChild = _children[childIndex - 1];
var stolenItem = leftChild._items.RemoveLast();
child._items.InsertAt(0, _items[childIndex - 1]);
_items[childIndex - 1] = stolenItem;
if (!leftChild.IsLeaf)
{
// 非葉子節點的子節點需要保證數量比item多1,item數量變了,子節點數量也要變
// 所以需要從左邊的子節點中移除最後一個子節點,然後插入到當前子節點的第一個位置
child._children.InsertAt(0, leftChild._children.RemoveLast());
}
}
else if (childIndex < ChildrenCount - 1 && _children[childIndex + 1].ItemsCount > _minItems)
{
// 如果右邊的子節點存在且右邊的子節點的item數量大於最小值,則從右邊的子節點借一個item
var child = _children[childIndex];
var rightChild = _children[childIndex + 1];
var stolenItem = rightChild._items.RemoveAt(0);
child._items.Add(_items[childIndex]);
_items[childIndex] = stolenItem;
if (!rightChild.IsLeaf)
{
// 非葉子節點的子節點需要保證數量比item多1,item數量變了,子節點數量也要變
// 所以需要從右邊的子節點中移除第一個子節點,然後插入到當前子節點的最後一個位置
child.AddChild(rightChild._children.RemoveAt(0));
}
}
else
{
// 如果當前節點左右兩邊的子節點的item數量都不大於最小值(例如正好等於最小值 t-1 ),則合併當前節點和右邊的子節點或者左邊的子節點
// 優先和右邊的子節點合併,如果右邊的子節點不存在,則和左邊的子節點合併
if (childIndex >= ItemsCount)
{
// ItemCount 代表最的子節點的索引,如果 childIndex 大於等於 ItemCount,說明右邊的子節點不存在,需要和左邊的子節點合併
childIndex--;
}
var child = _children[childIndex];
var mergeItem = _items.RemoveAt(childIndex);
var mergeChild = _children.RemoveAt(childIndex + 1);
child._items.Add(mergeItem);
child._items.AddRange(mergeChild._items);
child._children.AddRange(mergeChild._children);
}
return TryRemove(key, removeType, out item);
}
}
Benchmarks:與 優先佇列 PriorityQueue 的比較
我們實現的 BTree 支援自定義排序規則,也實現最值的刪除,意味著可以充當優先佇列使用。
我們使用 PriorityQueue 與 BTree 進行效能對比來看看 B樹 能否充當優先佇列使用。
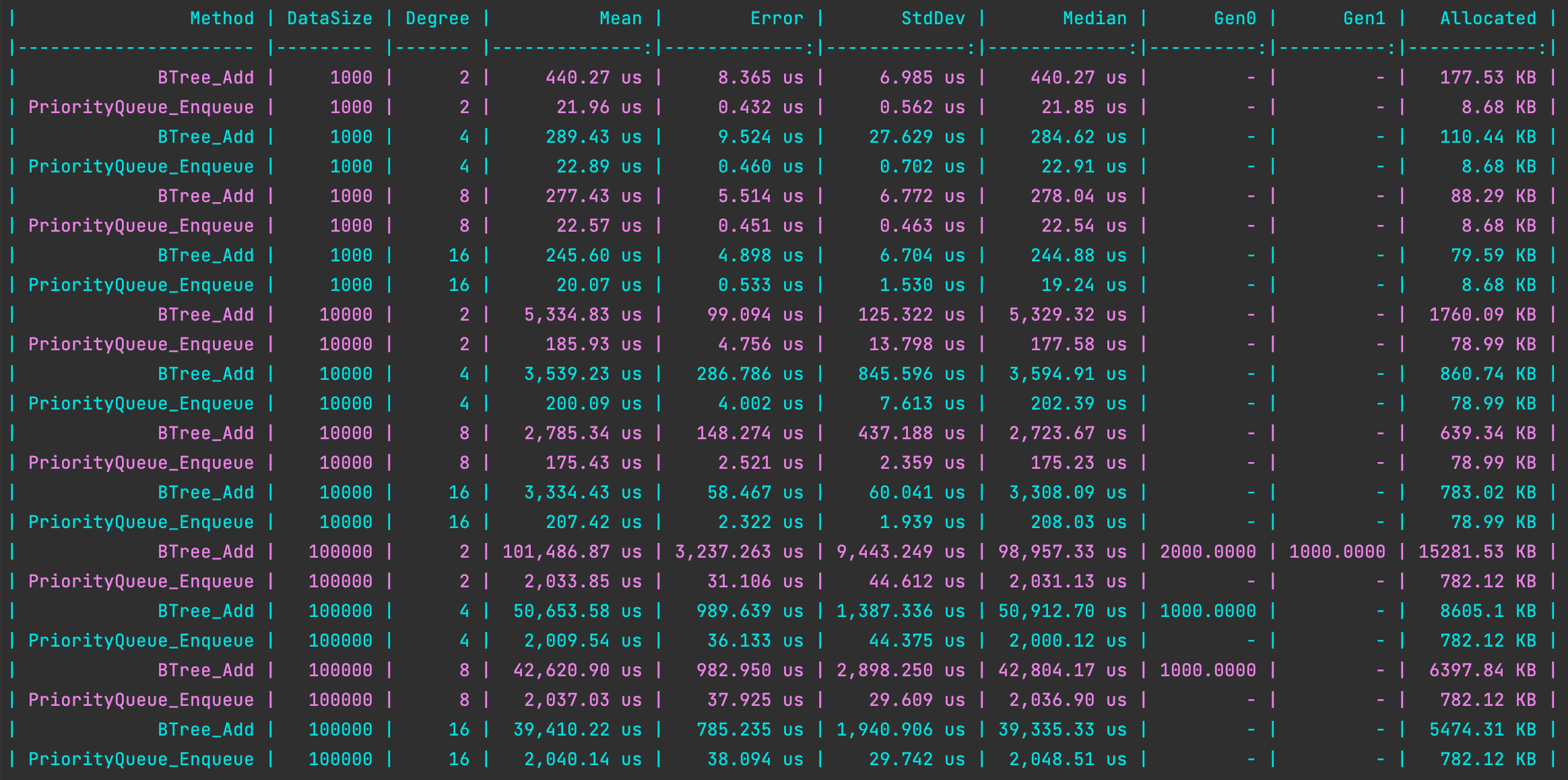
入隊效能
public class BTree_PriorityQueue_EnequeueBenchmarks
{
[Params(1000, 1_0000, 10_0000)] public int DataSize;
[Params(2, 4, 8, 16)] public int Degree;
private HashSet<int> _data;
[IterationSetup]
public void Setup()
{
var random = new Random();
_data = new HashSet<int>();
while (_data.Count < DataSize)
{
var value = random.Next();
_data.Add(value);
}
}
[Benchmark]
public void BTree_Add()
{
var btree = new BTree<int, int>(Degree);
foreach (var value in _data)
{
btree.Add(value, value);
}
}
[Benchmark]
public void PriorityQueue_Enqueue()
{
var priorityQueue = new PriorityQueue<int, int>(DataSize);
foreach (var value in _data)
{
priorityQueue.Enqueue(value, value);
}
}
}
出隊效能
public class BTree_PriorityQueue_DequeueBenchmarks
{
[Params(1000, 1_0000, 10_0000)] public int DataSize;
[Params(2, 4, 8, 16)] public int Degree;
private BTree<int, int> _btree;
private PriorityQueue<int, int> _priorityQueue;
[IterationSetup]
public void Setup()
{
var random = new Random();
_btree = new BTree<int, int>(Degree);
_priorityQueue = new PriorityQueue<int, int>(DataSize);
while (_btree.Count < DataSize)
{
var value = random.Next();
_btree.Add(value, value);
_priorityQueue.Enqueue(value, value);
}
}
[Benchmark]
public void BTree_Remove()
{
while (_btree.Count > 0)
{
_btree.RemoveMin();
}
}
[Benchmark]
public void PriorityQueue_Dequeue()
{
while (_priorityQueue.Count > 0)
{
_priorityQueue.Dequeue();
}
}
}
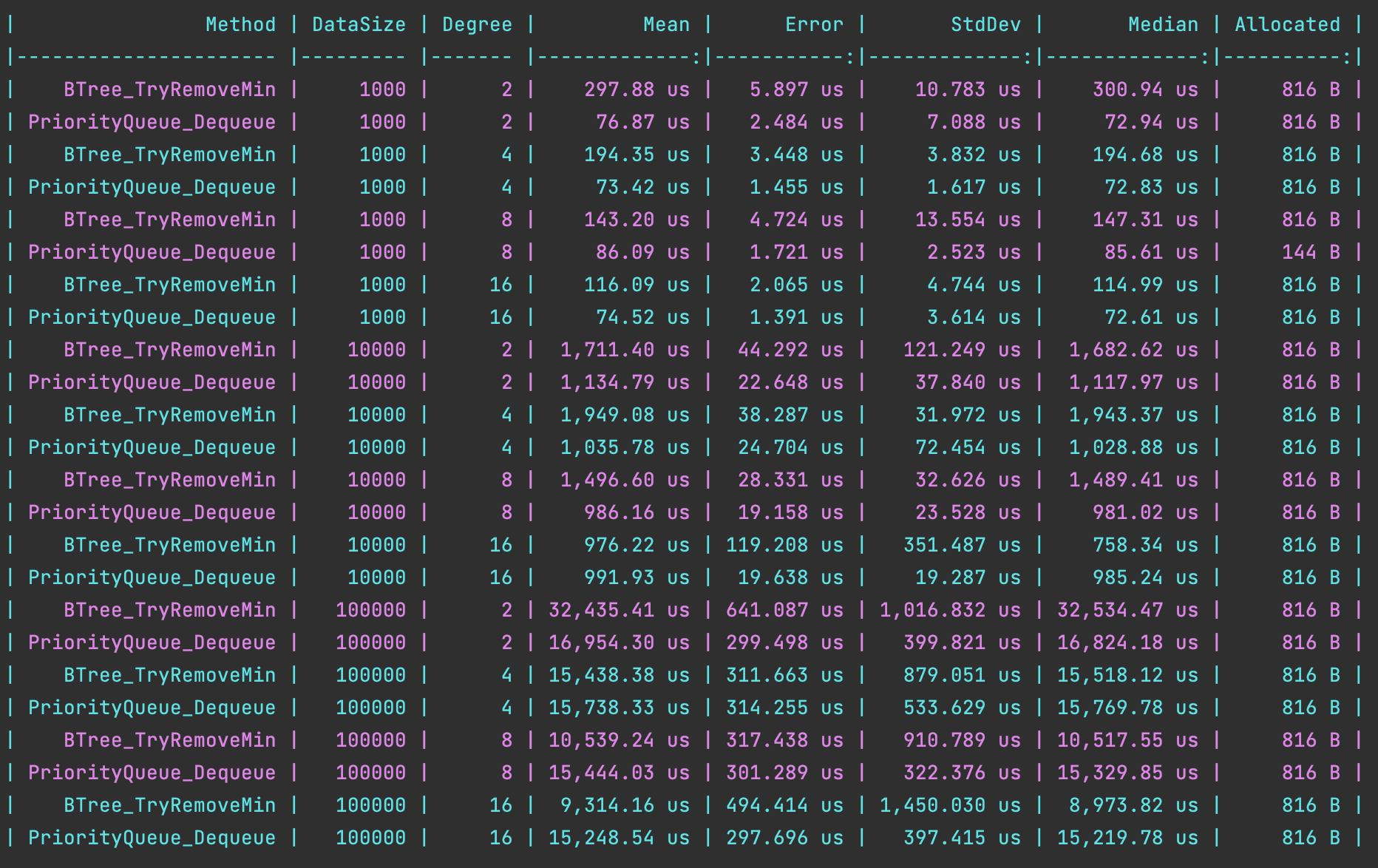
可以看到,B樹 雖然在入隊效能上比 PriorityQueue 差。但在資料量和 degree 較大時,出隊效能比 PriorityQueue 好,是有能力充當優先佇列使用的。
總結
B樹 在 degree 較大時,樹的高度較低,刪除的效率較高,可充當優先佇列使用。
B樹 的插入,刪除,查詢都是基於遞迴的,遞迴的深度為樹的高度。
B樹 對資料的查詢基於二分查詢,時間複雜度為 O(log n),B樹 的插入和刪除基於 B樹的查詢演演算法,都要找到資料所在的節點,然後在該節點進行插入和刪除。因此,B樹 的插入和刪除的時間複雜度也為 O(log n)。
B樹 是對二元樹的一種優化,使得樹的高度更低,但是在插入,刪除的過程中,需要進行大量的節點分裂,合併,借用,交換等操作,使得演演算法的複雜度更高。
參考資料
Google 用 Go 實現的記憶體版 B樹 https://github.com/google/btree
B樹 維基百科 https://zh.m.wikipedia.org/zh-hans/B樹