樹

樹的表示方法

雙親表示法

用一組地址連續的儲存單元來存放樹中的各個節點，每一個節點中有一個資料域和一個指標域，資料域用來儲存樹中該節點本身的值；另一個指標域用來儲存該節點的雙親節點在儲存結構中的位置資訊。

採用雙親連結串列儲存方式實現查詢一個指定節點的雙親節點比較方便，但難以實現查詢一個指定節點的孩子節點。

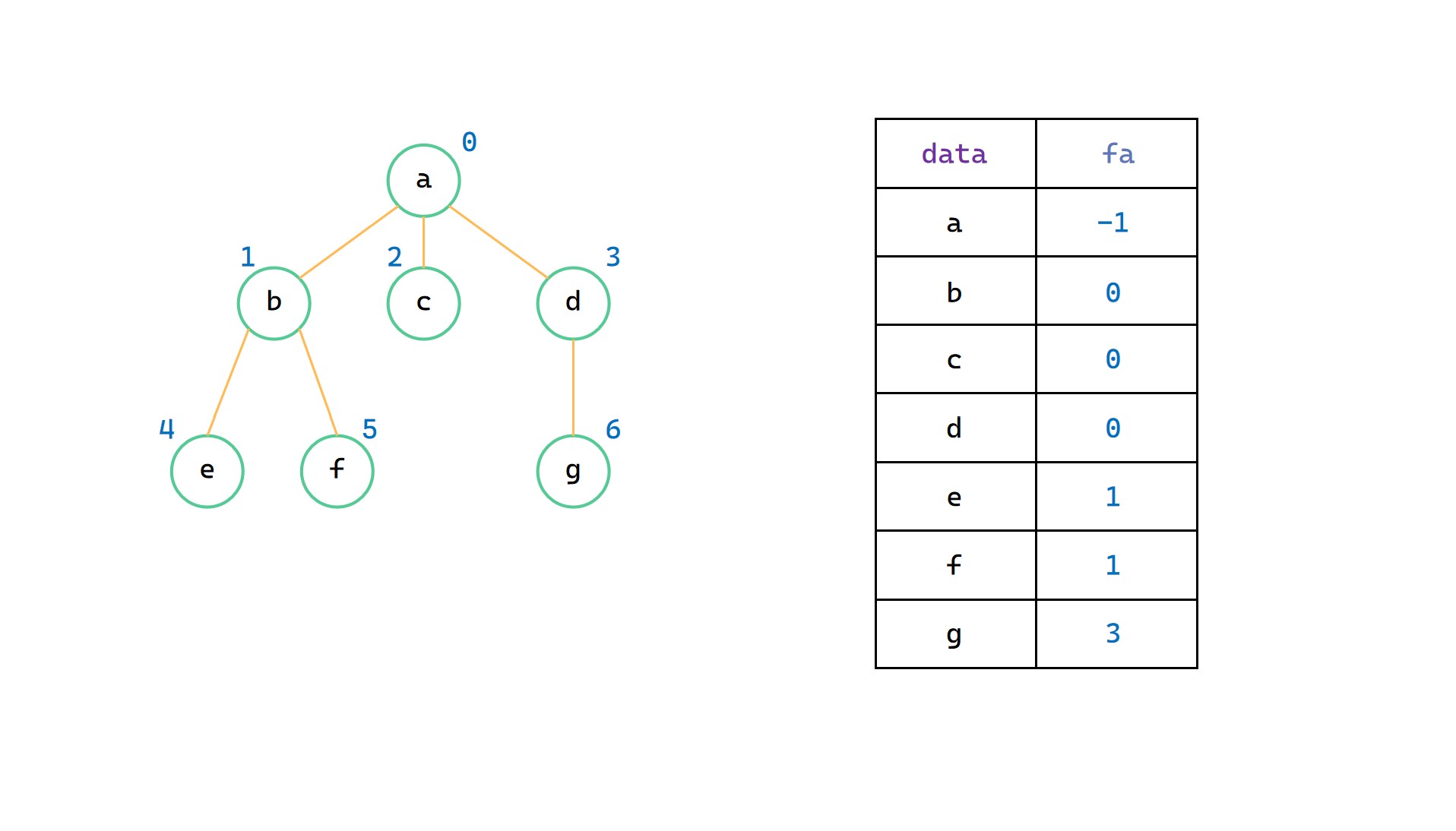
孩子表示法

用一組地址連續的儲存單元來存放樹中的各個節點，每一個節點有一個資料域和一個指標域，資料域用來儲存樹中該節點的值；另一個指標域用來存放該節點的孩子連結串列的頭指標。形式上有點像儲存圖的領接表。

採用孩子表示法便於實現查詢樹中指定節點的孩子節點，但難以實現查詢樹中指定節點的雙親節點。

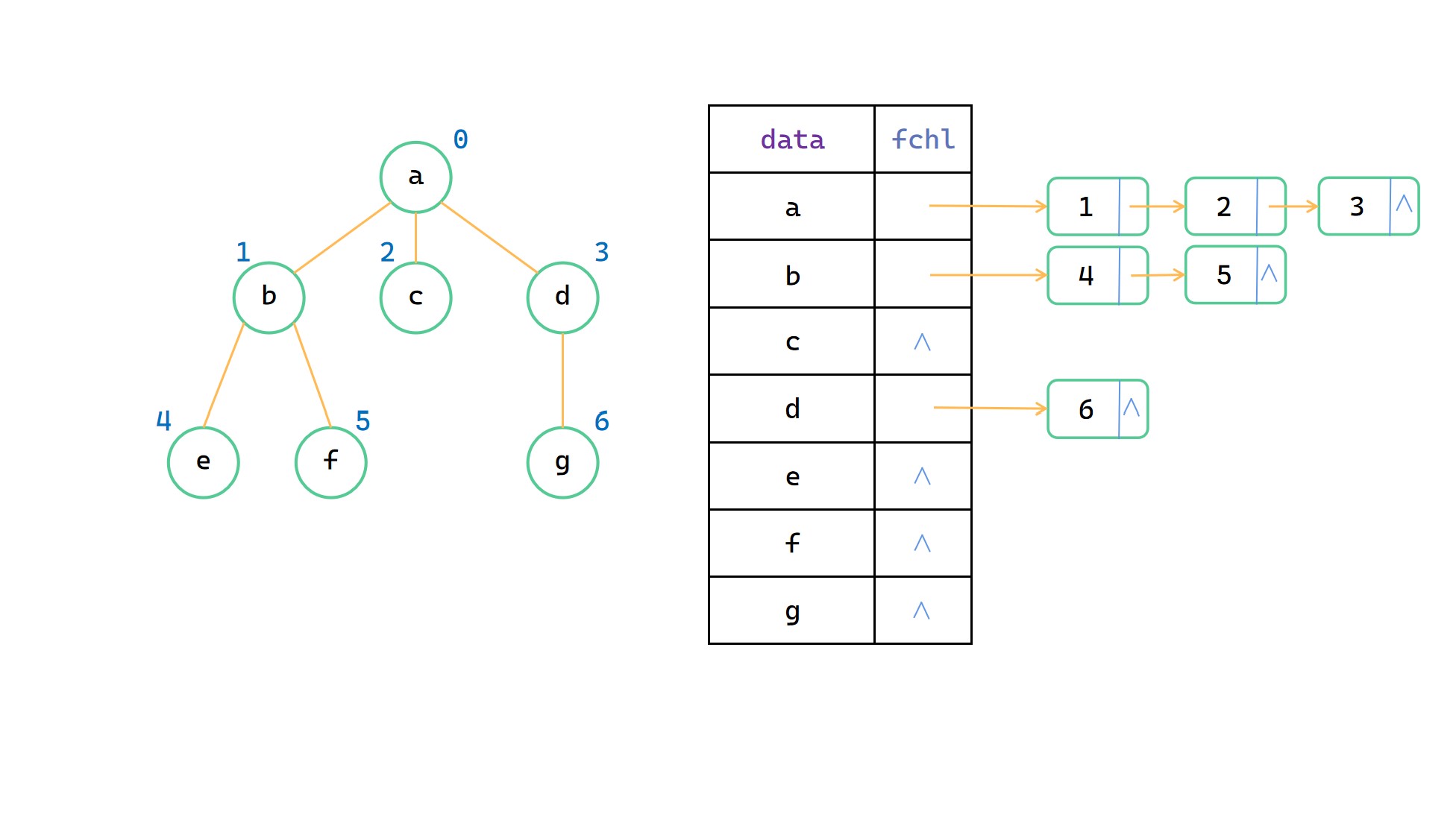
孩子兄弟表示法

孩子兄弟表示法是用一種鏈式的結構儲存一顆樹的方式。每個節點含有孩子指標域和兄弟指標域。我們分別用 firstchild 和 nextsibling 表示。
其中孩子指標域，表示指向當前結點的第一個孩子結點，兄弟結點表示指向當前結點的下一個兄弟結點。其本質是先將一棵樹轉換為二元樹後儲存在二叉鏈式結構之中。

孩子兄弟表示法能夠將對一棵樹的操作轉換成對二元樹的操作，這種表示方法在實際運用中比較廣泛。

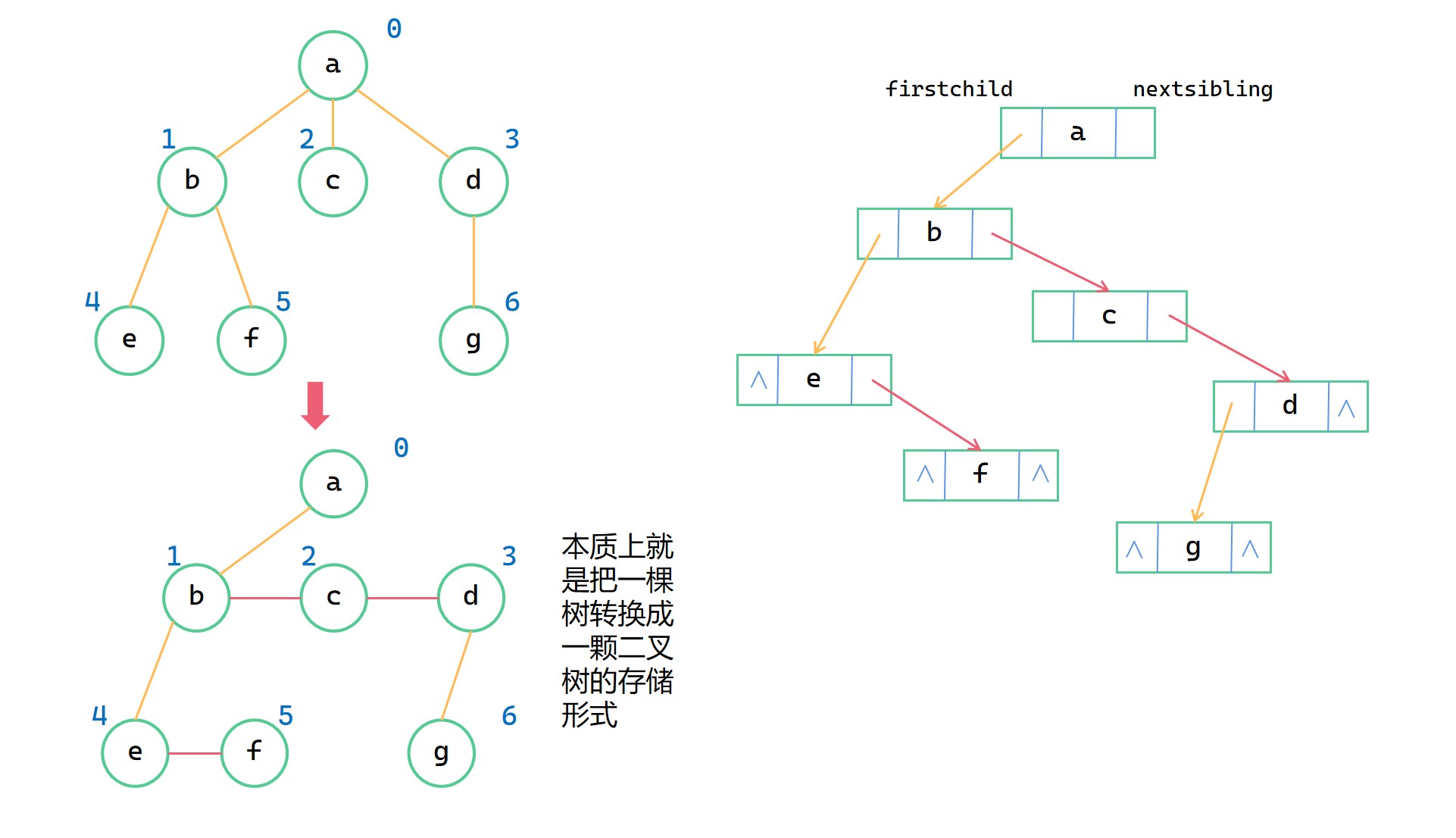
故在這裡給出孩子兄弟表示法建立樹的程式碼，在後文中也都是使用這種表示方法。

孩子兄弟表示法建立樹

typedef char Elemtype;
//樹 (孩子兄弟表示法)
typedef struct CSNode{

    Elemtype data;
    struct CSNode *firstchild;      //第一個孩子
    struct CSNode *nextsibling;     //下一個兄弟

}CSNode, *CSTree;

//建立 樹
CSTree Create_CSTree(){
    Elemtype data;
    CSTree T;
    scanf("%c", &data);                       //輸入節點資料
    getchar();

    if(data == '#')        //輸入 - 以停止建立子樹
        return NULL;
    T = (CSTree)malloc(sizeof(CSNode));
    T->data = data;

    printf("輸入 %c 的第一個孩子資料(#停止): ", data);  //遞迴建立
    T->firstchild = Create_CSTree();
    printf("輸入 %c 的下一個兄弟資料(#停止): ", data);  
    T->nextsibling = Create_CSTree();
 
    return T;
}

二元樹

二元樹是節點度數不大於 2 的有序樹，是簡單而又廣泛運用的重要資料結構。

二元樹基本結構

//二元樹 結構體
typedef struct BiNode{

    Elemtype data;
    struct BiNode *leftchild;       //左兒子
    struct BiNode *rightchild;      //右兒子

}BiNode, *BinaryTree;

森林

森林很好理解，就是多個樹組成的集合。

森林基本結構

//森林 結構體
typedef struct {

    CSTree ct[MAX];
    int n;   //樹的個數
	
}forest, *Forest;

樹、二元樹和森林的轉換

樹轉換為二元樹

樹 --> 二元樹步驟

（1）將樹中每個相鄰的兄弟進行連線；
（2）將每個節點除第一個孩子以外，斷開其他兄弟與其雙親節點的連線；
（3）適當旋轉處理完後的樹，使其呈現二元樹的形式。

樹 --> 二元樹圖解

（1）加線、（2）斷線

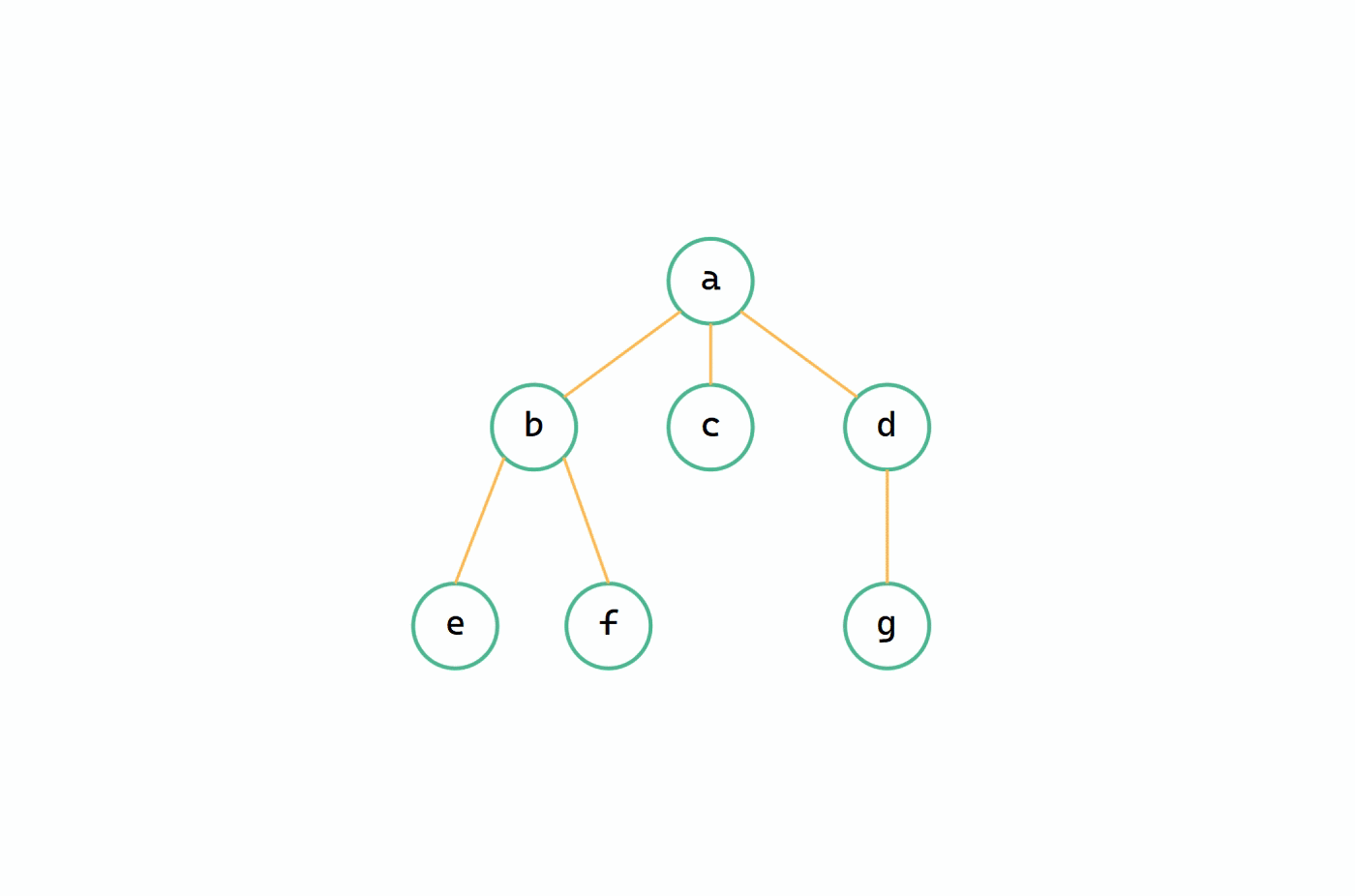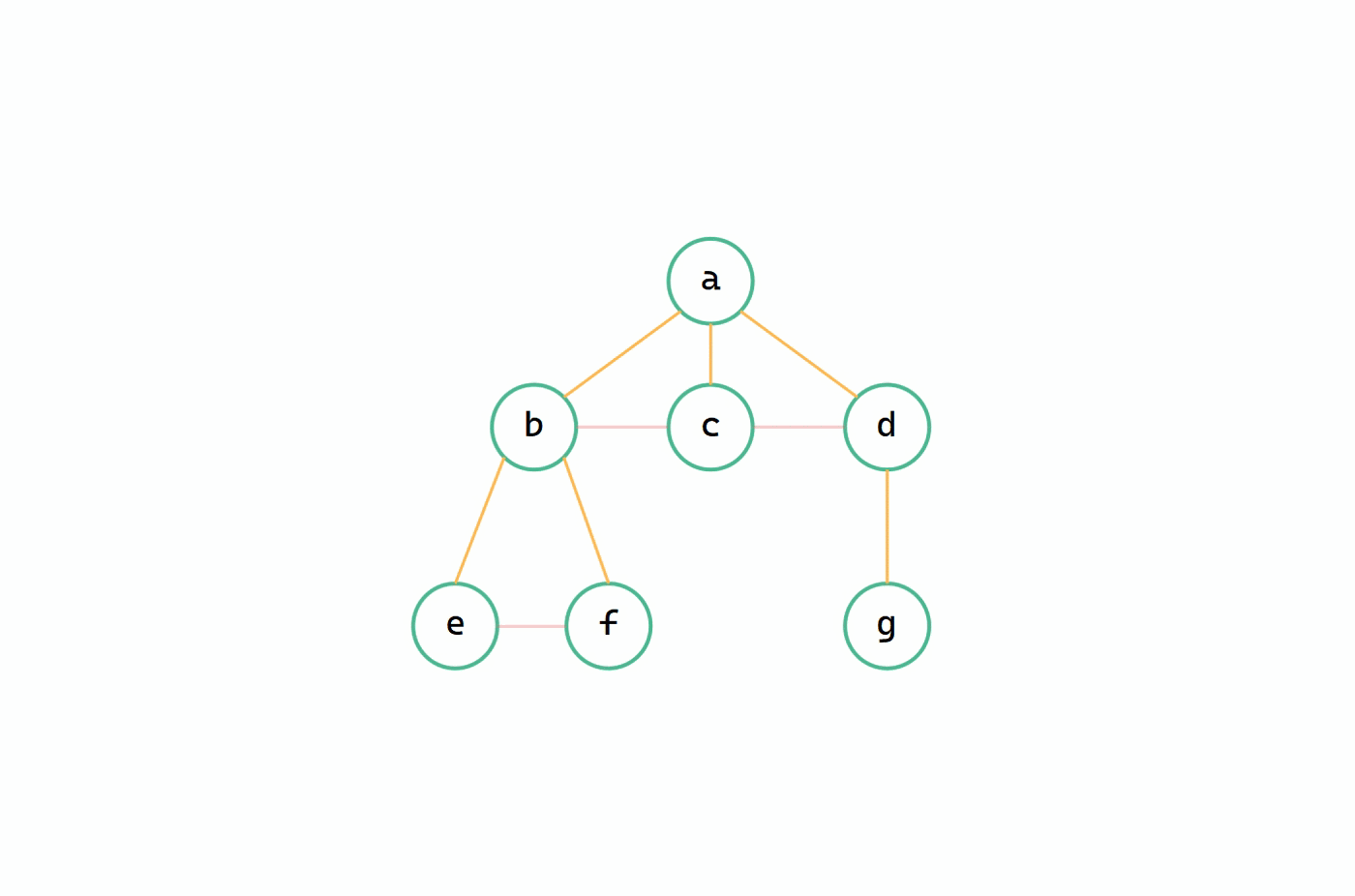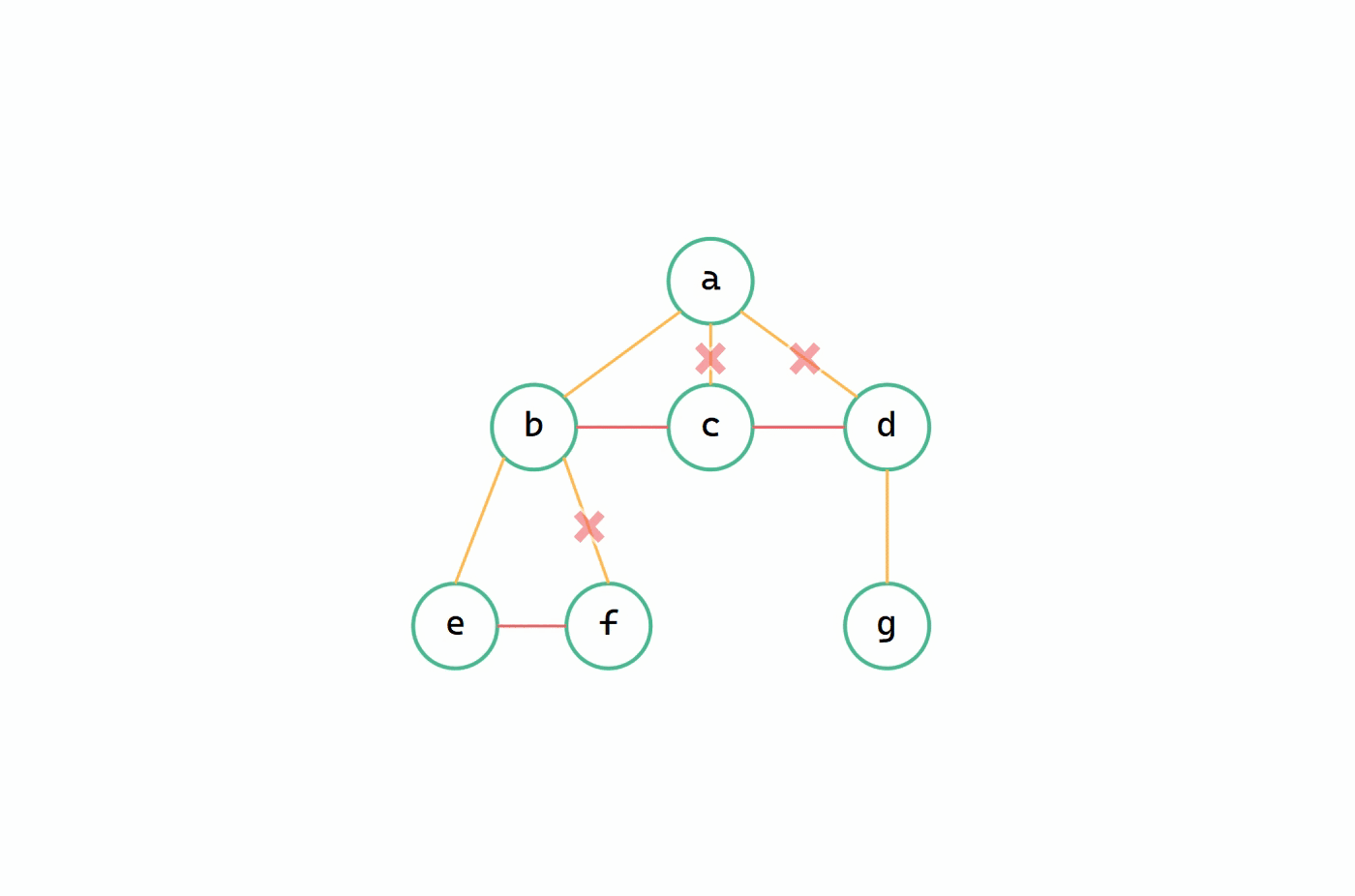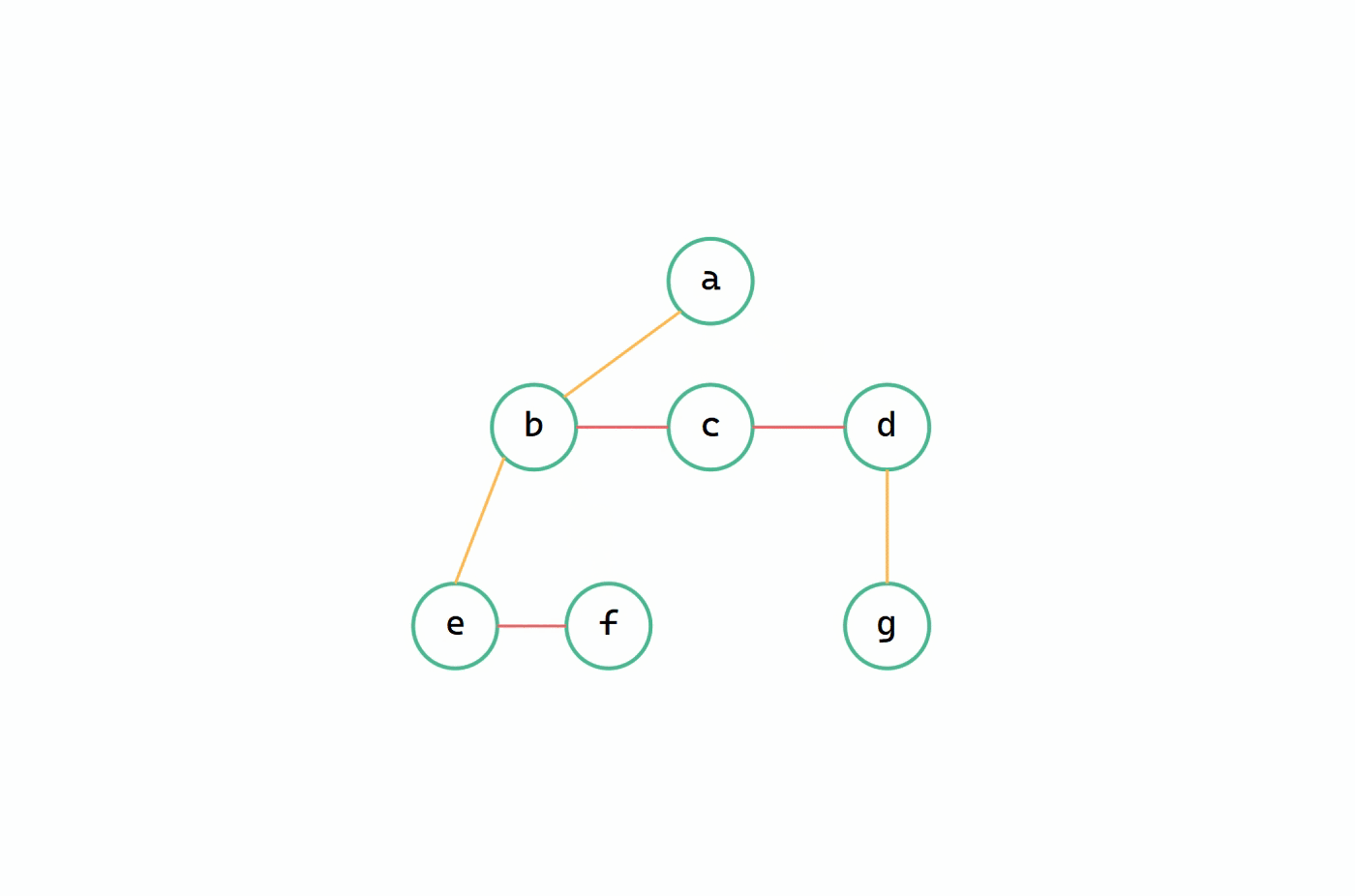
（3）適當旋轉

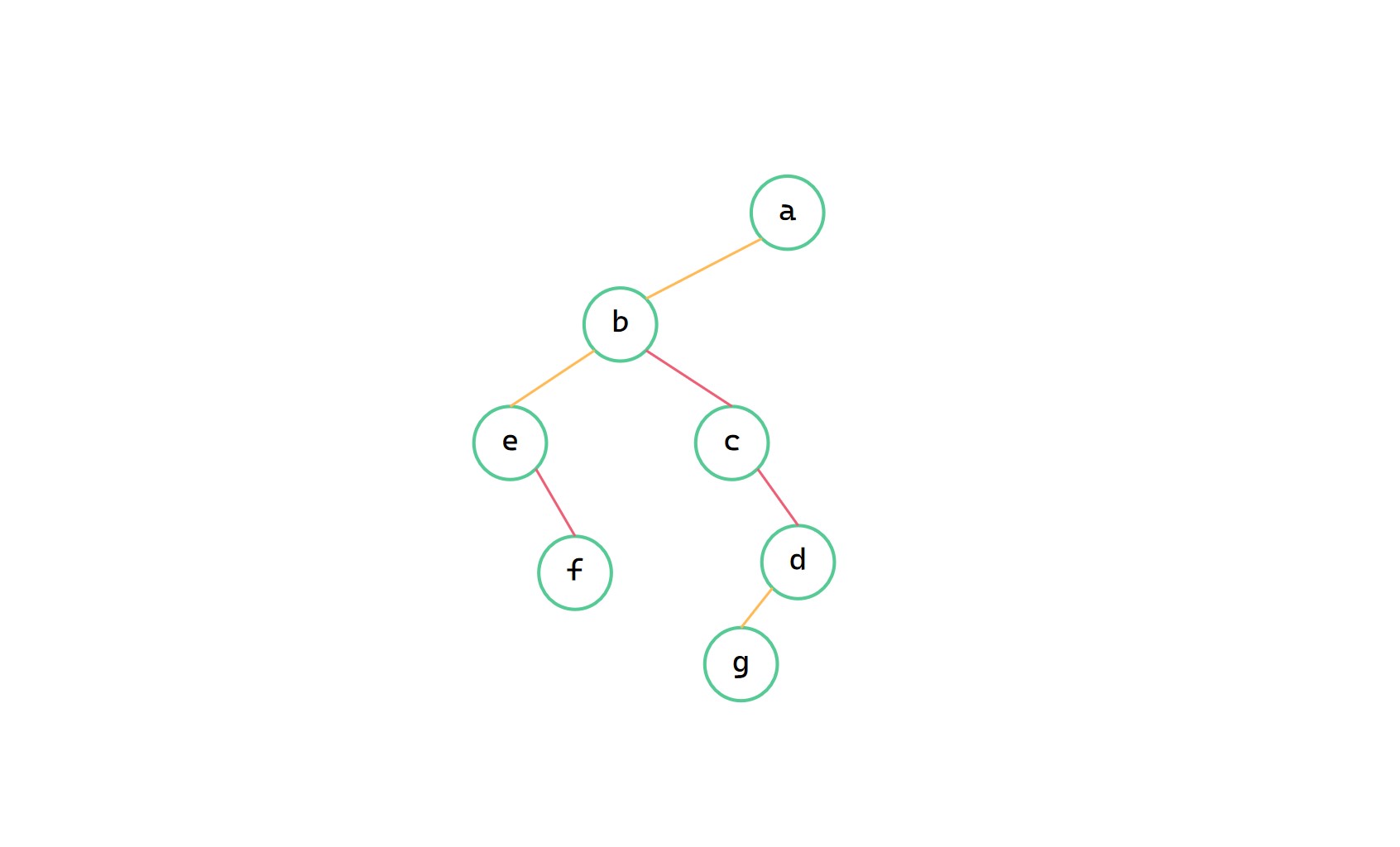
由於我們使用的是孩子兄弟表示法，其實本質上用了類似二元樹的結構儲存了樹。所以樹的 firstchild 對應了需要轉換成的二元樹的 leftchild，而 nextsibling 對應了需要轉換成的二元樹的 rightchild。我們只需要遞迴操作使其一一對應相等即可。

樹 --> 二元樹程式碼

//樹 轉化為 二元樹
BinaryTree CSTree_Transform_to_BinaryTree(CSTree ct){
    if(!ct) return NULL;

    BinaryTree T = (BinaryTree)malloc(sizeof(BiNode));
    T->data = ct->data;
    //相當於將left變為firstchild, 將right變為nextsibling 本質的形態沒有改變
    T->leftchild = CSTree_Transform_to_BinaryTree(ct->firstchild);
    T->rightchild = CSTree_Transform_to_BinaryTree(ct->nextsibling);

    return T;
}

二元樹轉換為樹

二元樹 --> 樹步驟

（1）先將二元樹的所有右孩子調整至同一層；
（2）若某個節點為雙親節點的左孩子，將該節點的沿右邊的左右節點與其雙親節點連線；
（3）刪除同一層所有橫向的連線。

二元樹 --> 樹圖解

（1）調整至同一層

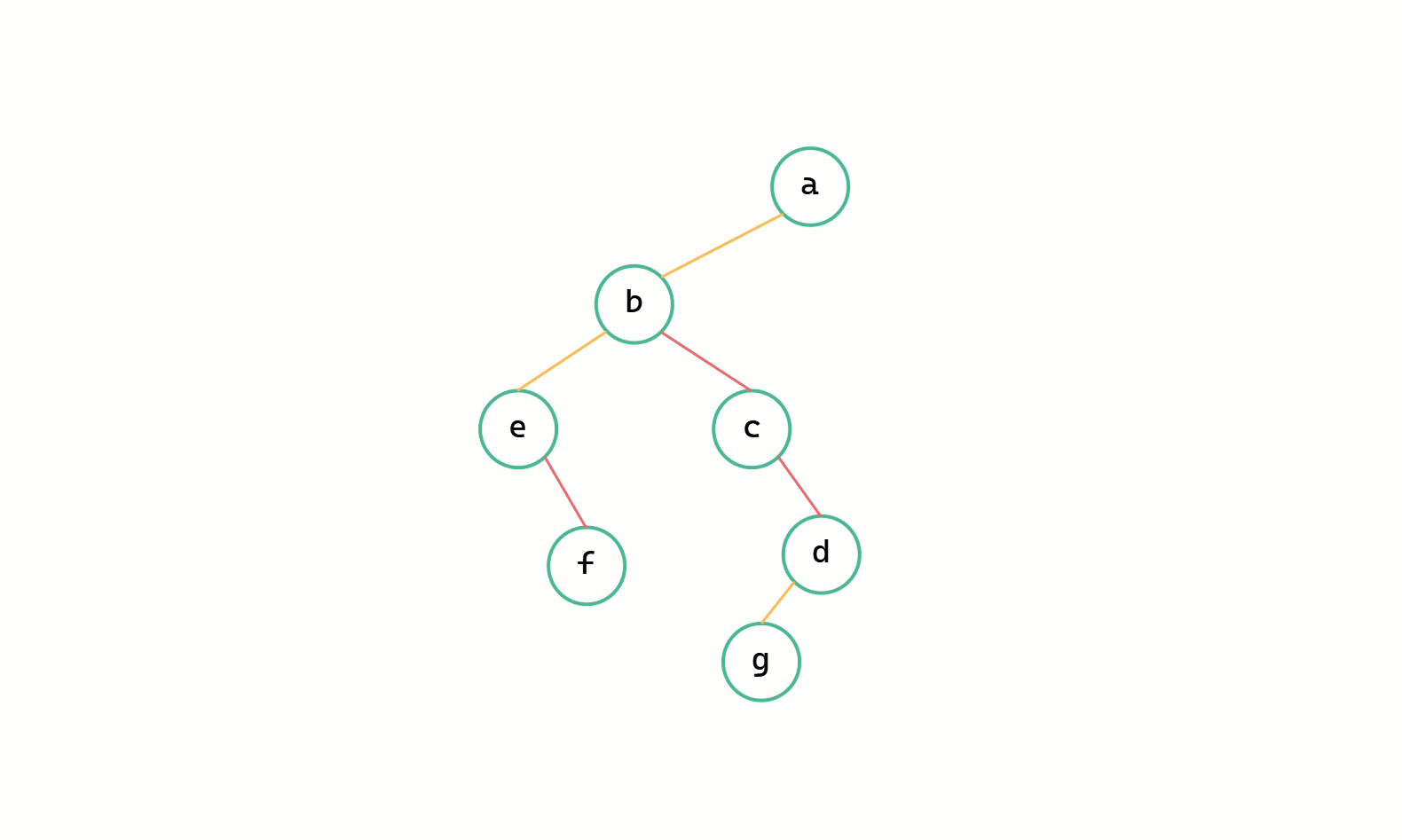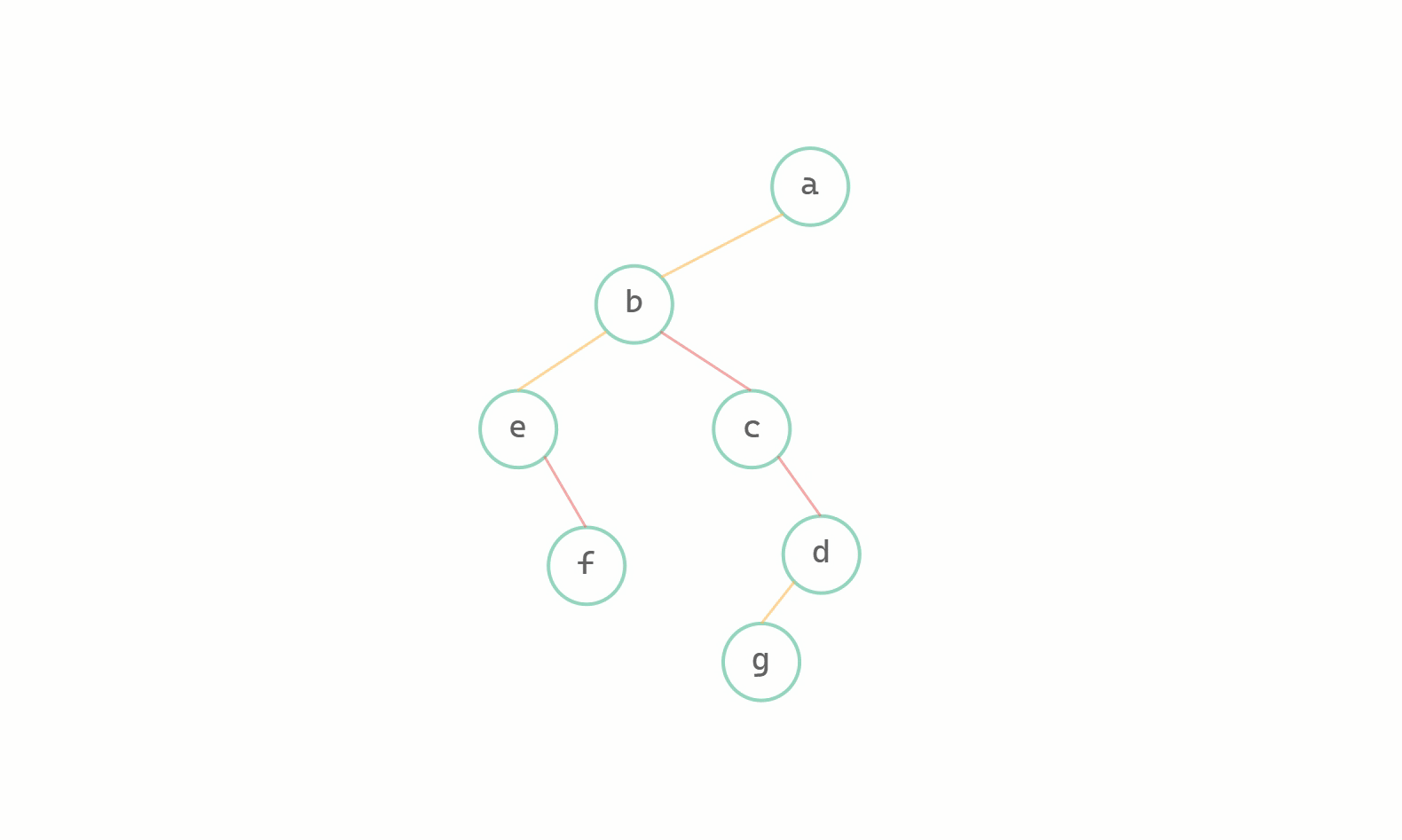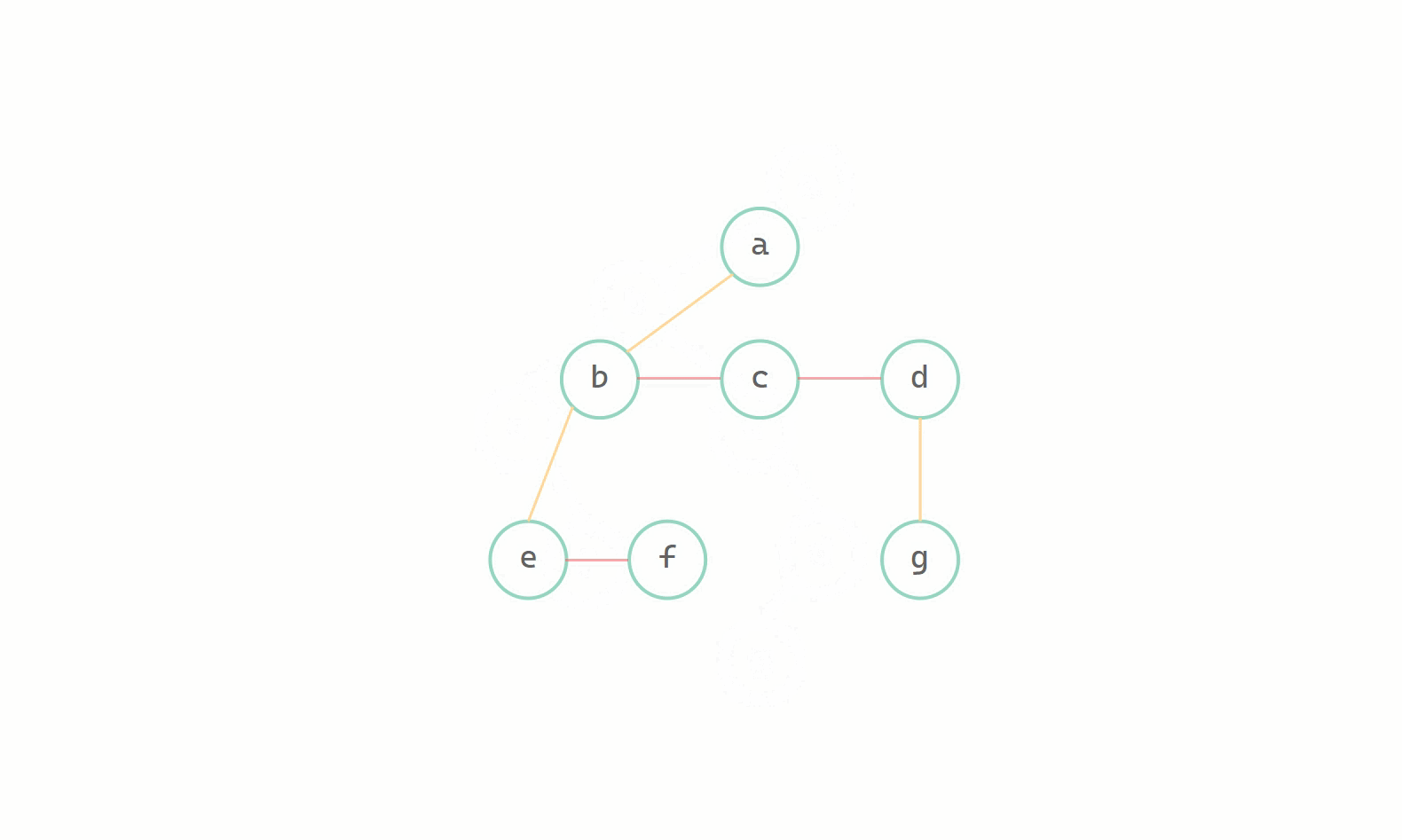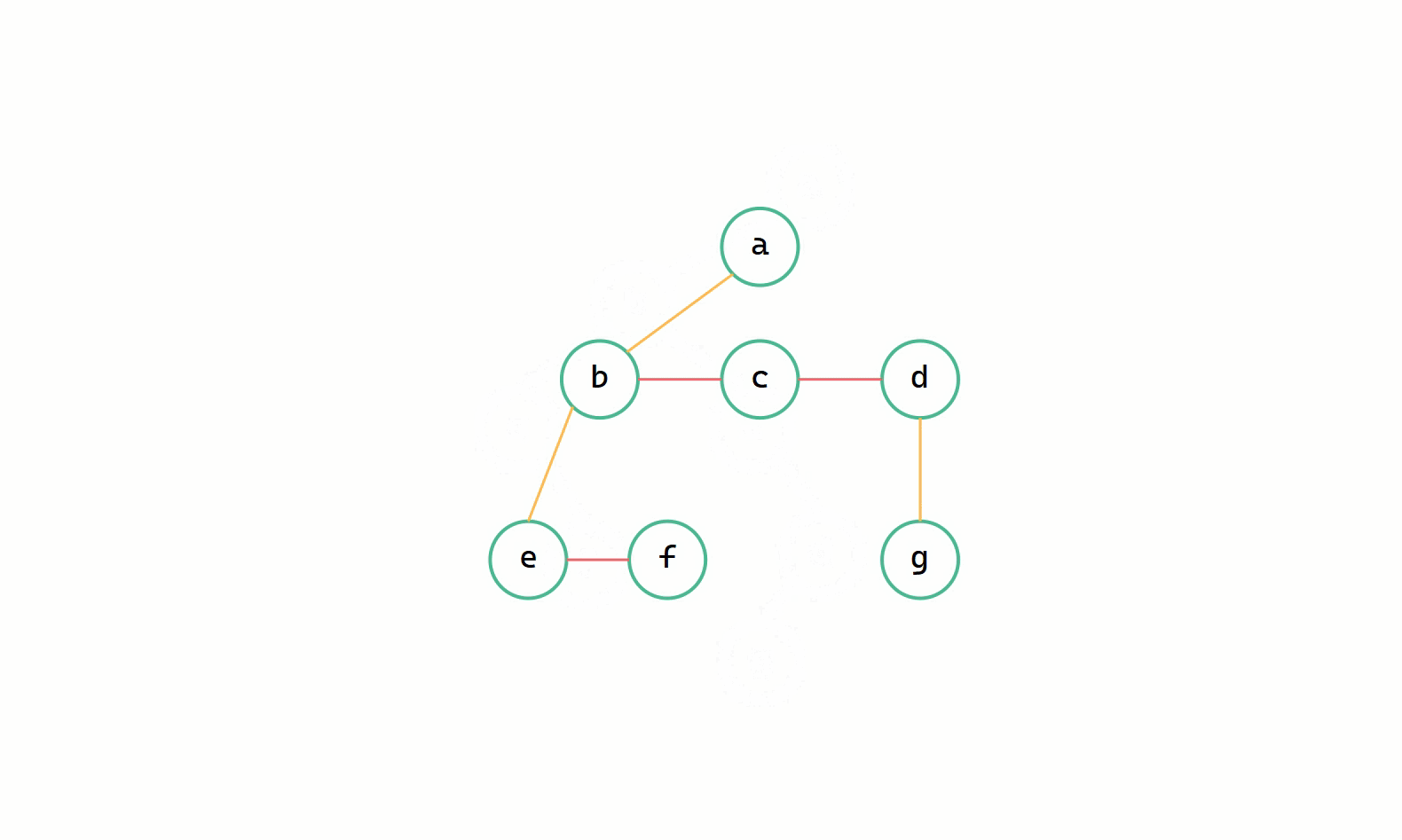
（2）加線、（3）斷線

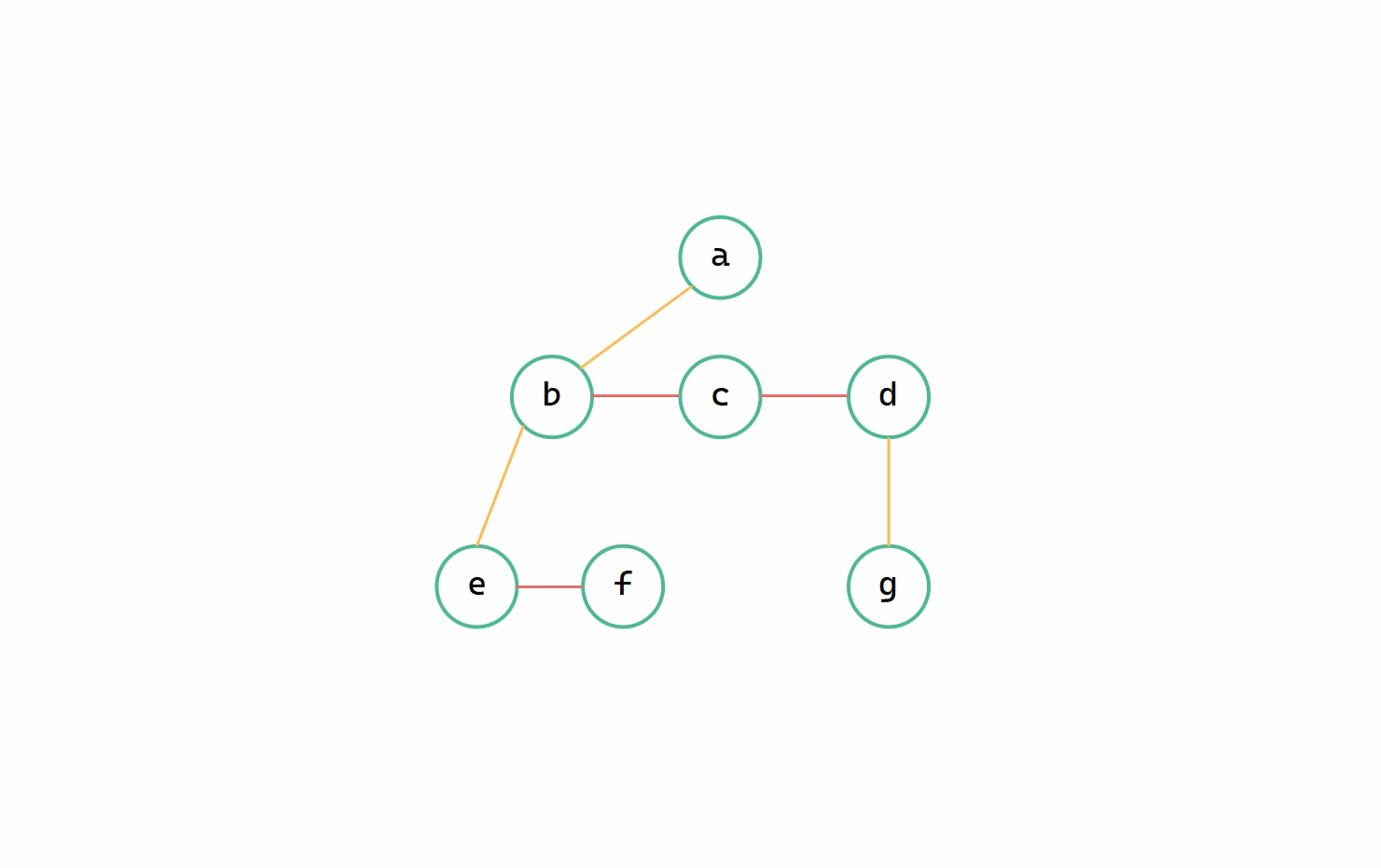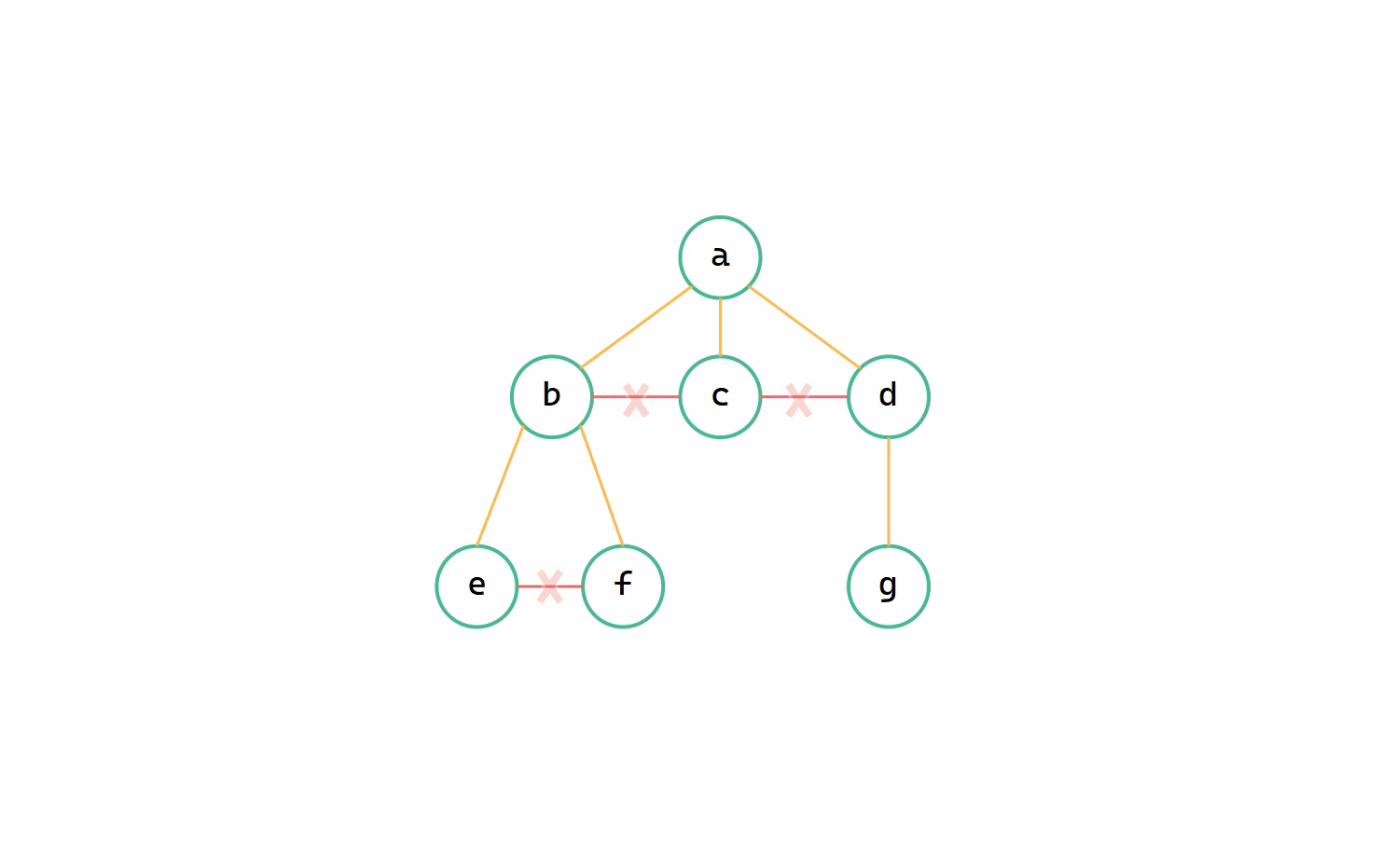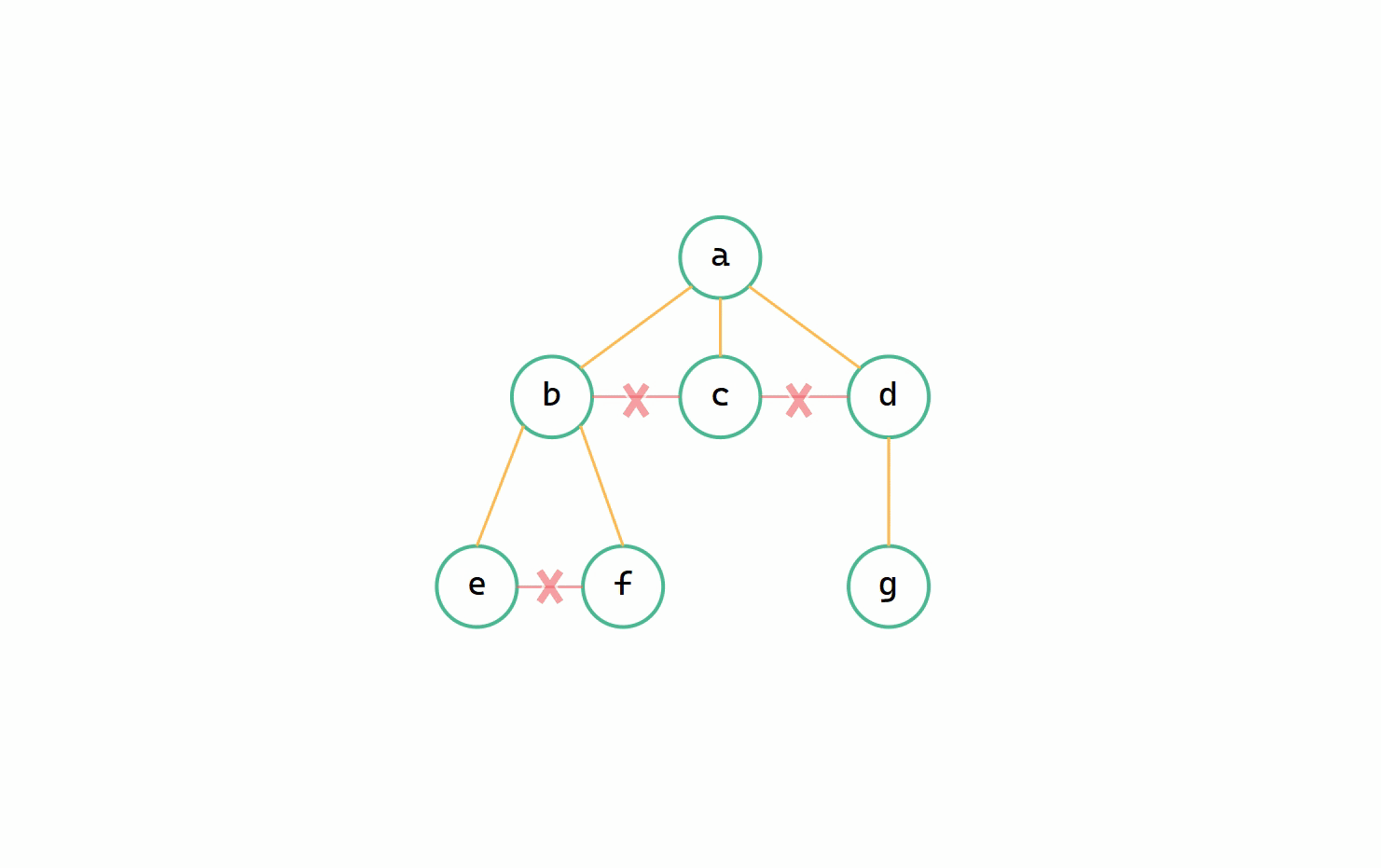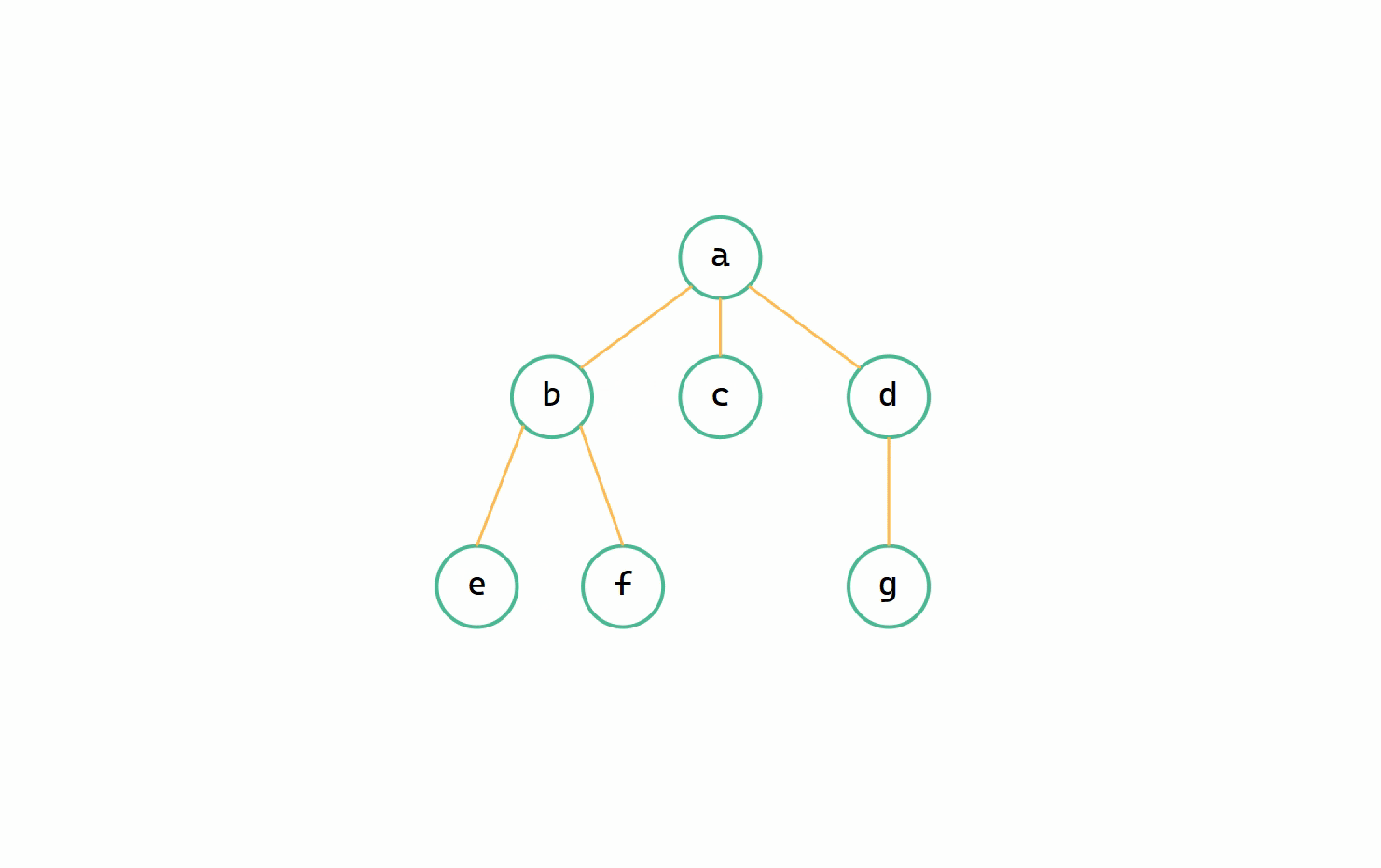
二元樹轉換為樹其實就是樹轉換為二元樹逆運算，本質上都是一致的，同樣只需要遞迴操作使得 leftchild 等於 firstchild ，rightchild 等於 nextsibling 即可

二元樹 --> 樹程式碼

//二元樹 轉化 為樹
CSTree BinaryTree_Transform_to_CSTree(BinaryTree bt){
    if(!bt)  return NULL;

    CSTree T = (CSTree)malloc(sizeof(CSNode));
    T->data = bt->data;
    //相當於將firstchild變為left, 將nextsibling變為right 本質的形態沒有改變
    T->firstchild = BinaryTree_Transform_to_CSTree(bt->leftchild);
    T->nextsibling = BinaryTree_Transform_to_CSTree(bt->rightchild);

    return T;
}

森林轉換為二元樹

森林 --> 二元樹步驟

（1）將森林的每個樹轉換為二元樹；
（2）將每個二元樹按照原順序將其根節點通過右孩子依次連線，變成一整個二元樹。

森林 --> 二元樹圖解

（1）每個樹變成二元樹（2）按照順序通過右孩子連線

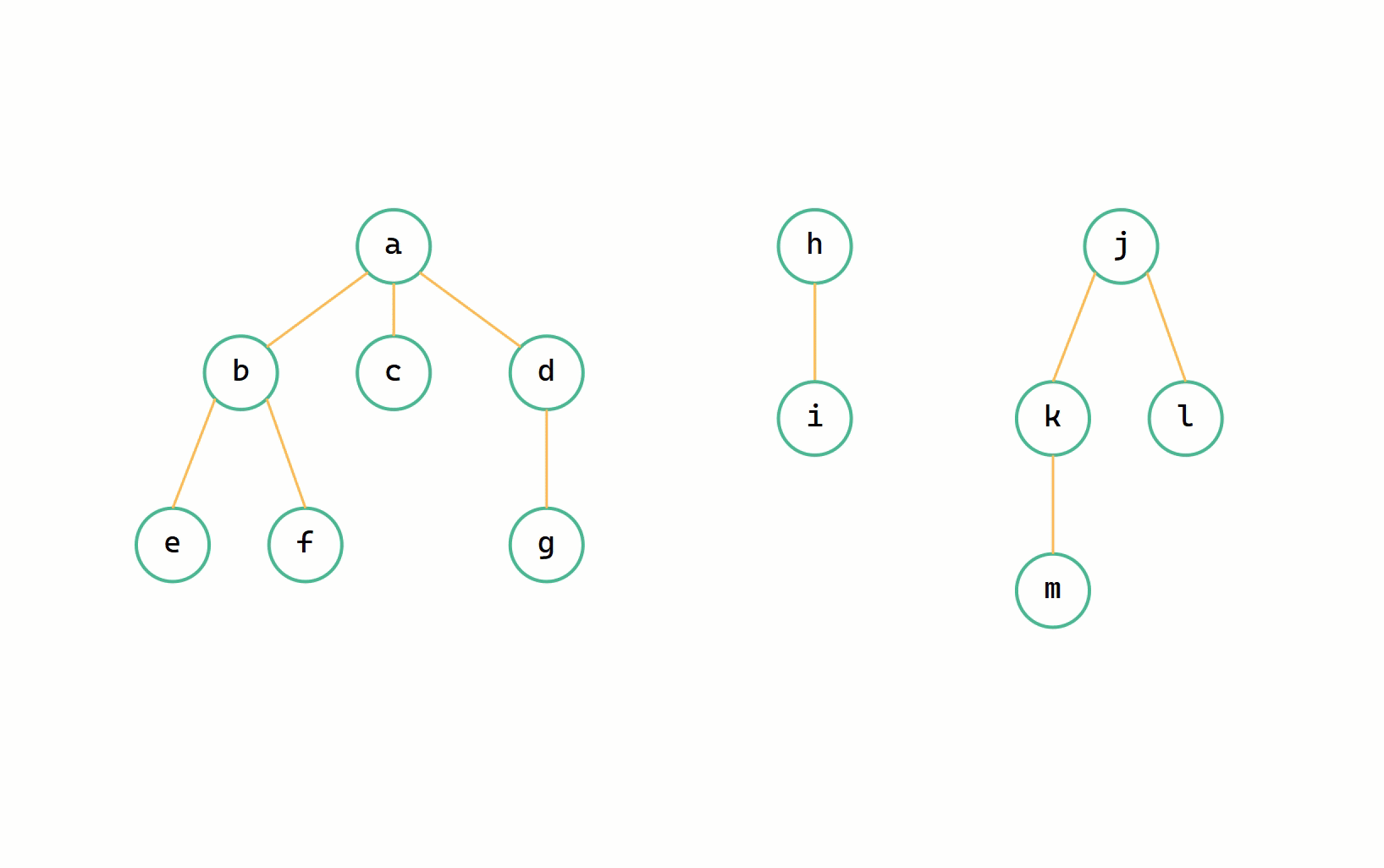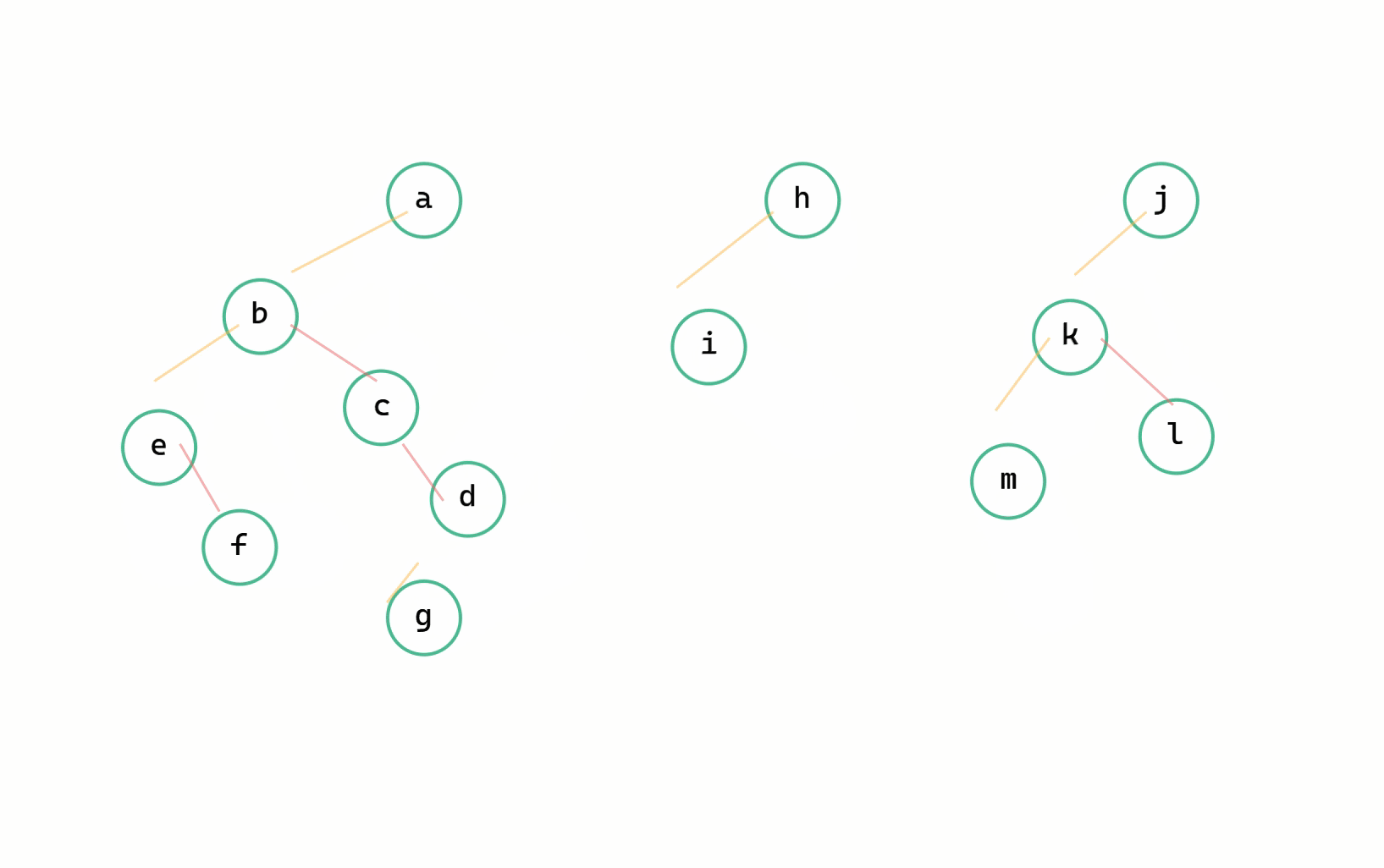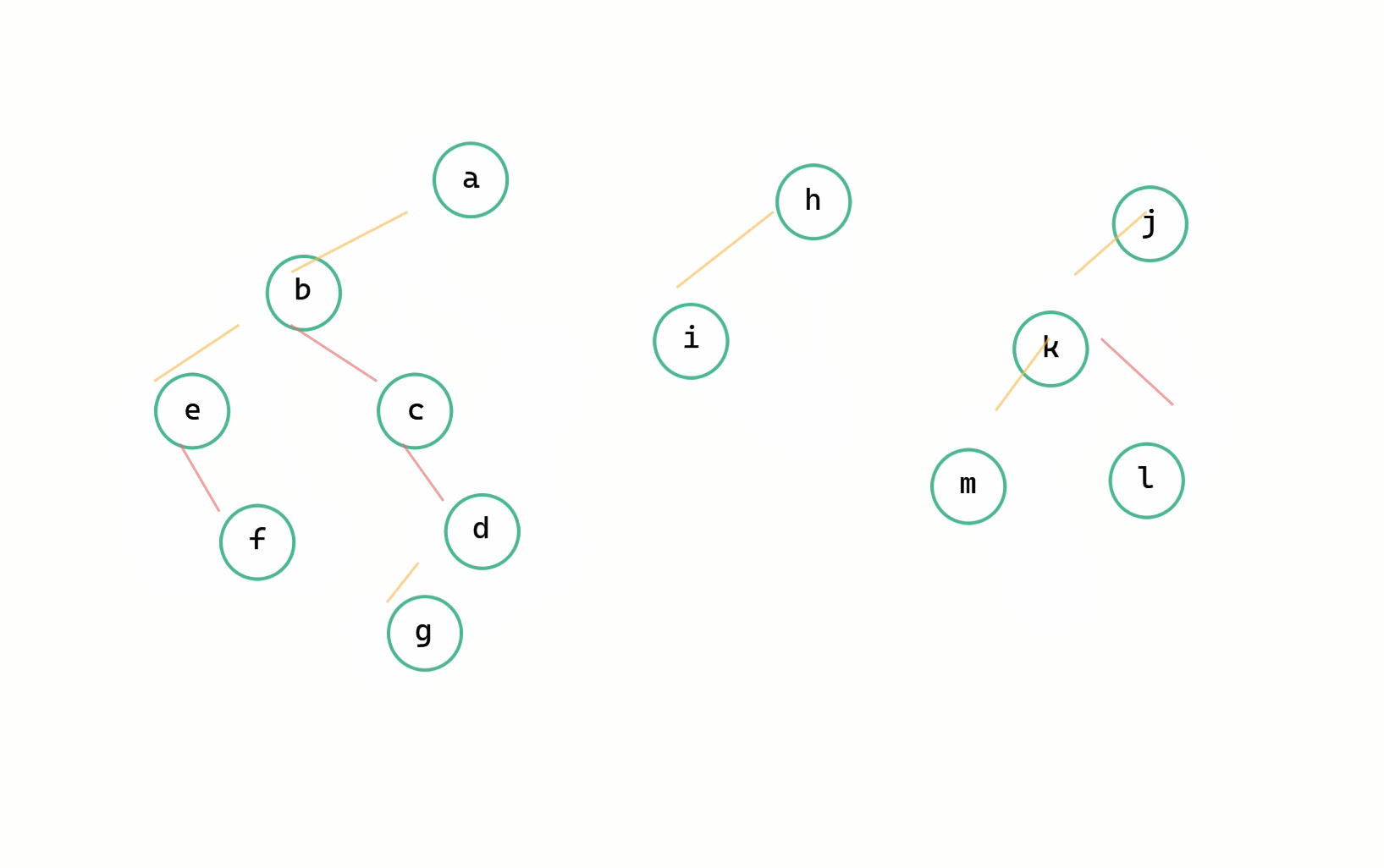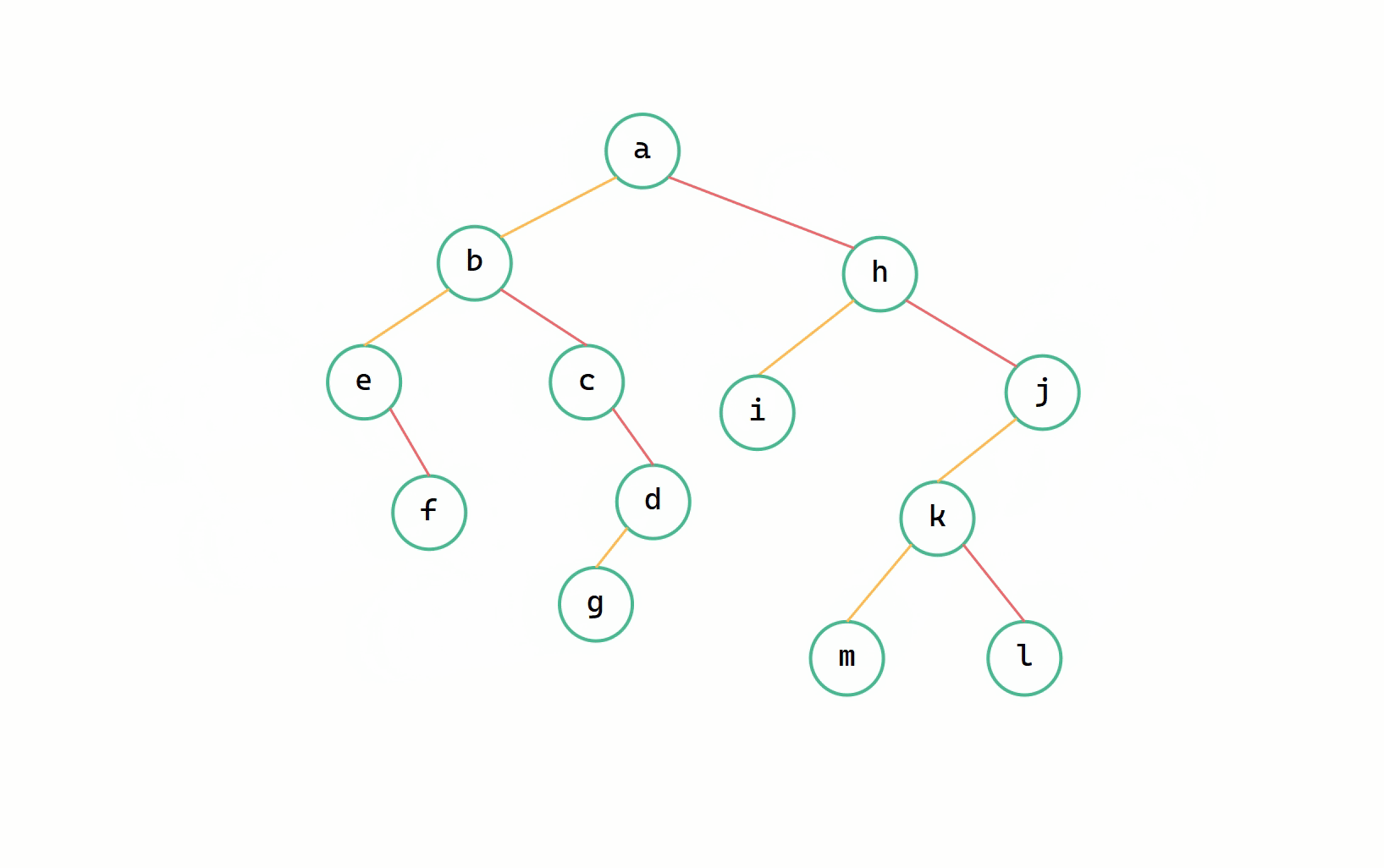
森林用的是順序的結構來儲存多個樹，因此我們只需要用 low 標記一下當前樹的位置下標，當遞迴操作到達 high 時，就停止遞迴。

森林 --> 二元樹程式碼

//森林 轉化為 二元樹
BinaryTree Forest_Transform_to_BinaryTree(CSTree ct[], int low, int high){
    if(low > high)  return NULL;
  
    //每個樹變成二元樹
    BinaryTree T = CSTree_Transform_to_BinaryTree(ct[low]);  
    //通過rightchild連線每一個二元樹的根節點
    T->rightchild = Forest_Transform_to_BinaryTree(ct, low + 1, high);

    return T;
}

二元樹轉換為森林

在上面森林轉換為二元樹的過程中，我們可以發現，二元樹從根節點沿右下方的所有節點正好對應了森林每個樹的根節點，我們從這一點出發，進行森林轉換為二元樹的逆運算，就可以完成二元樹轉換為森林的操作。

二元樹 --> 森林步驟

（1）斷開二元樹根節點沿右下方孩子節點所有的連線，分成多個二元樹；
（2）將每個二元樹轉換為樹，形成森林。

二元樹 --> 森林圖解

（1）斷線

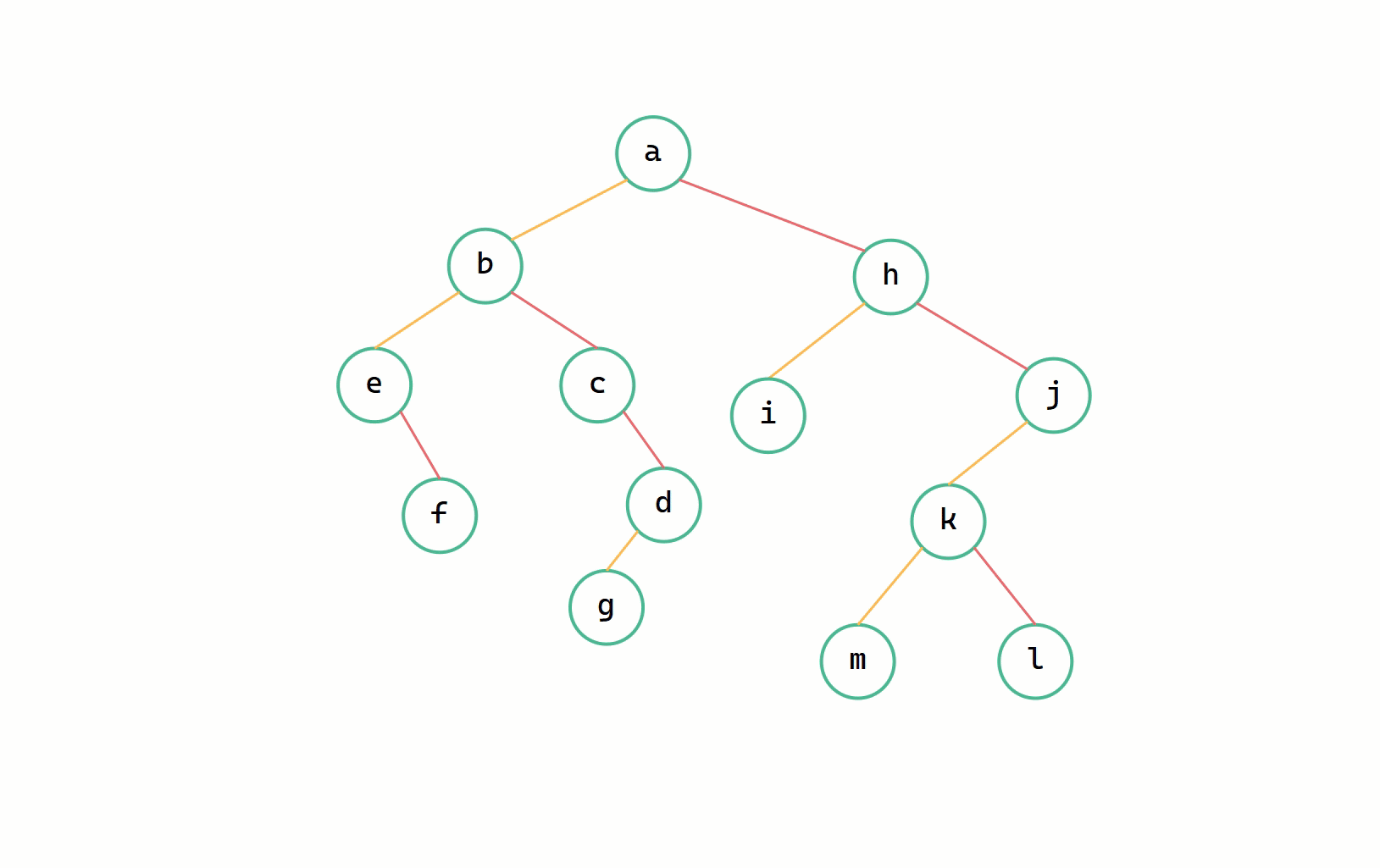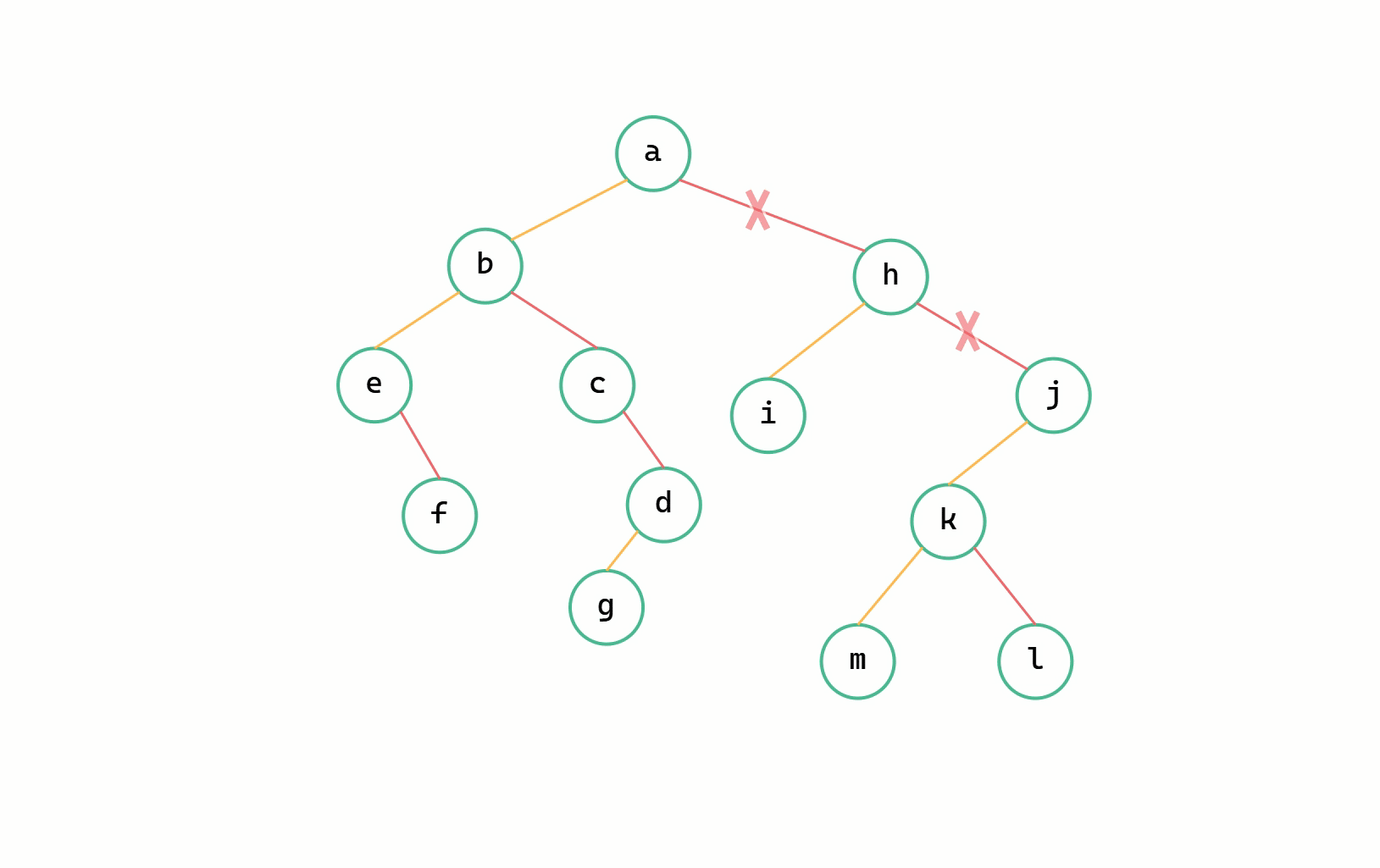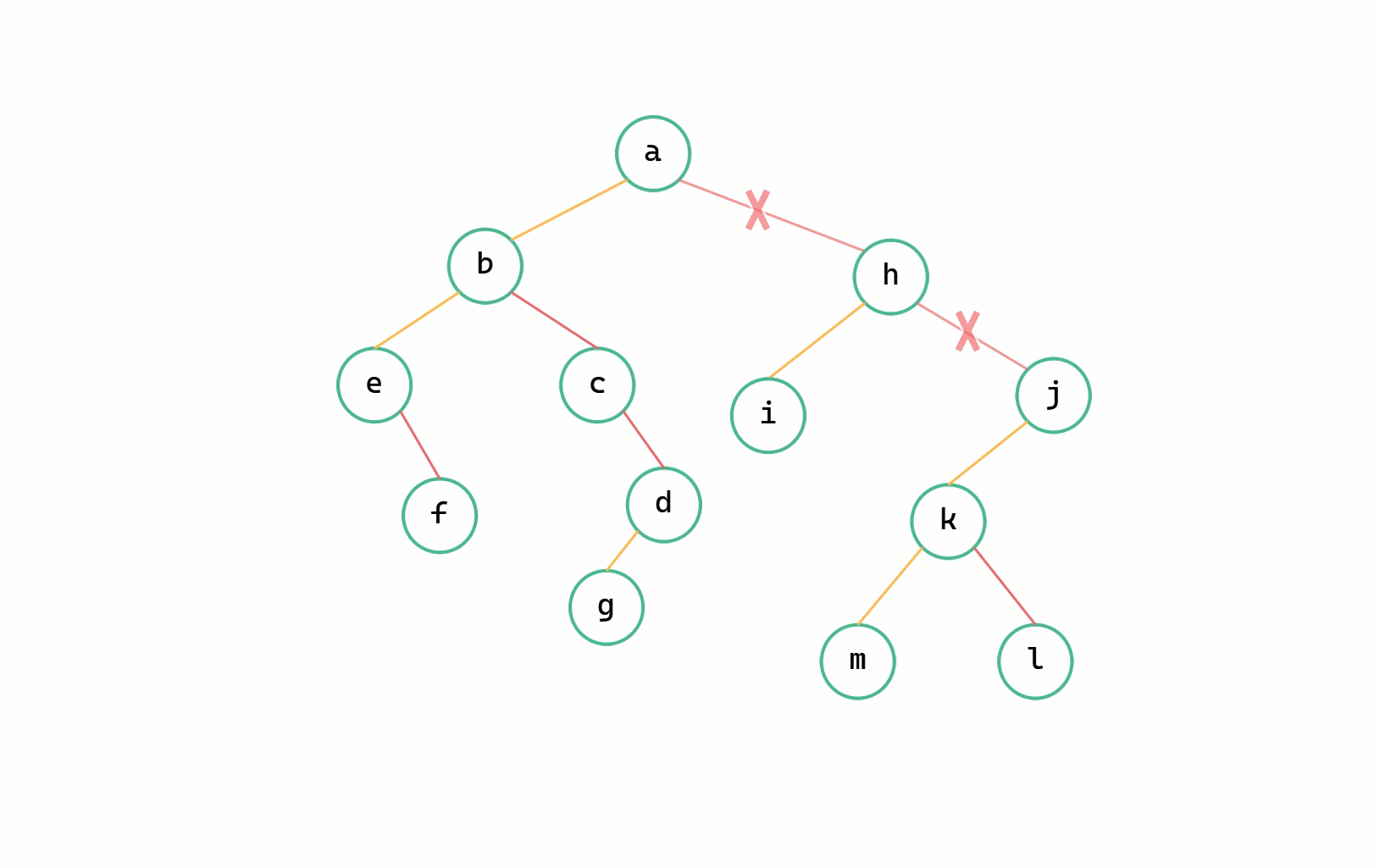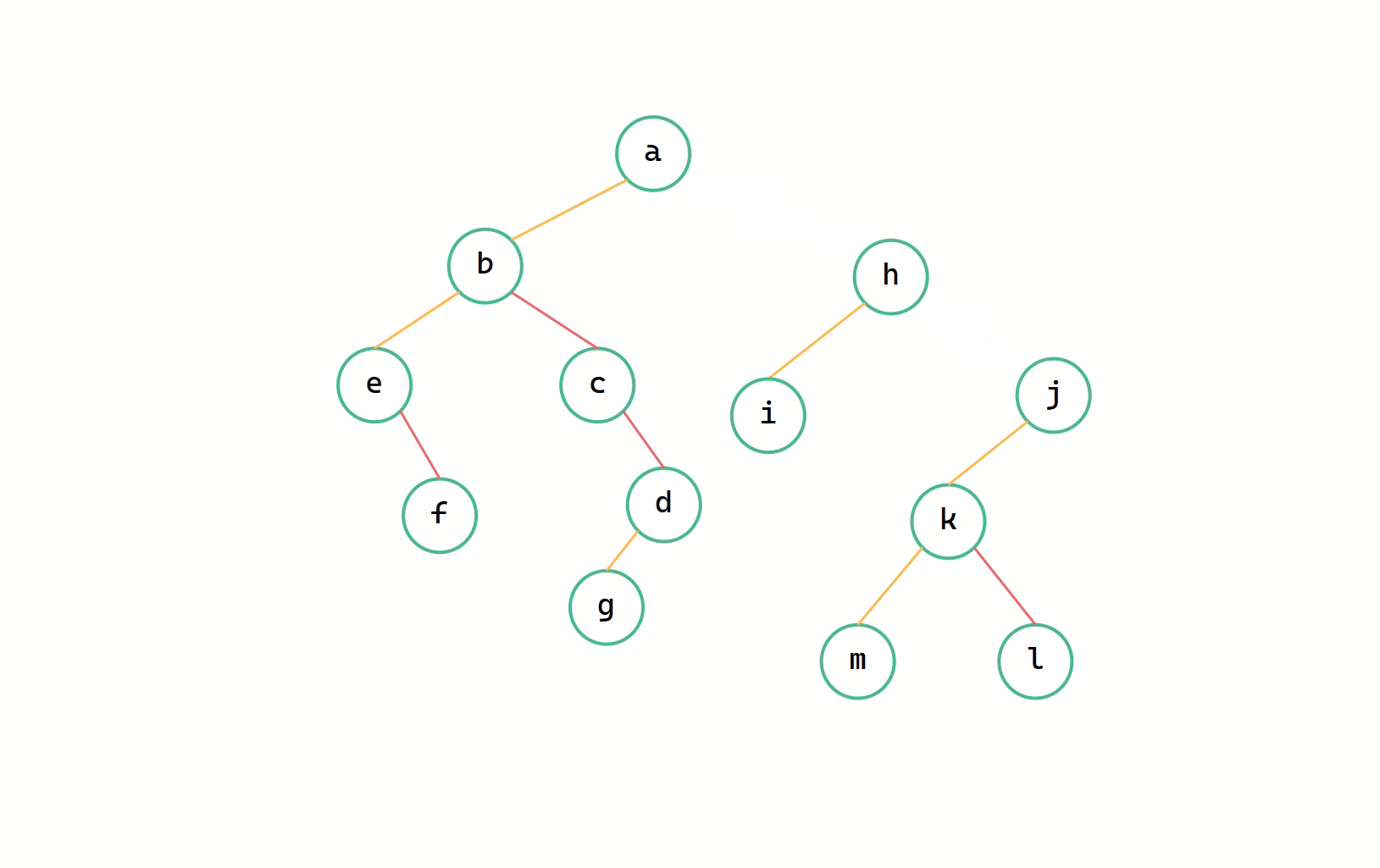
（2）每個二元樹轉換為樹

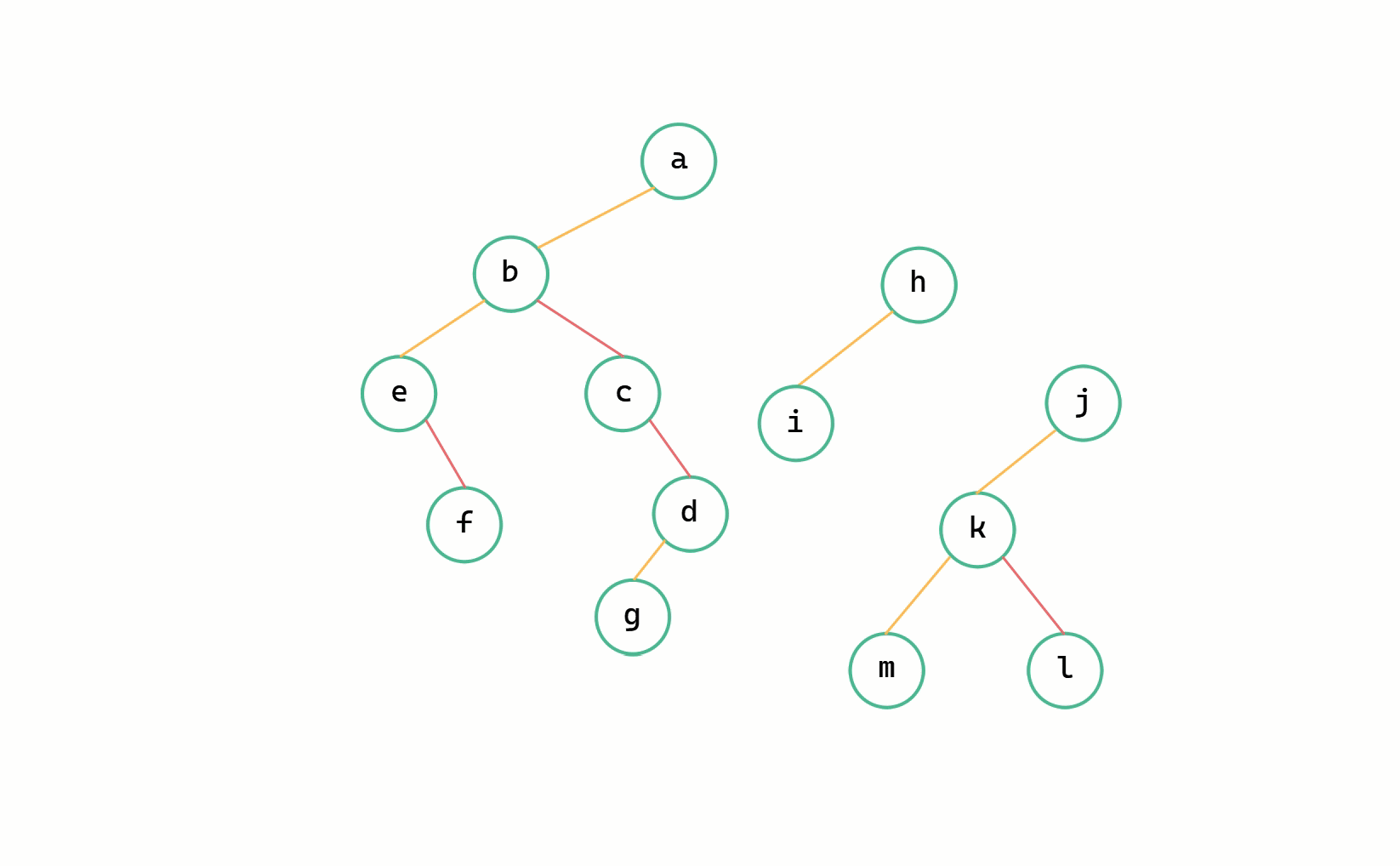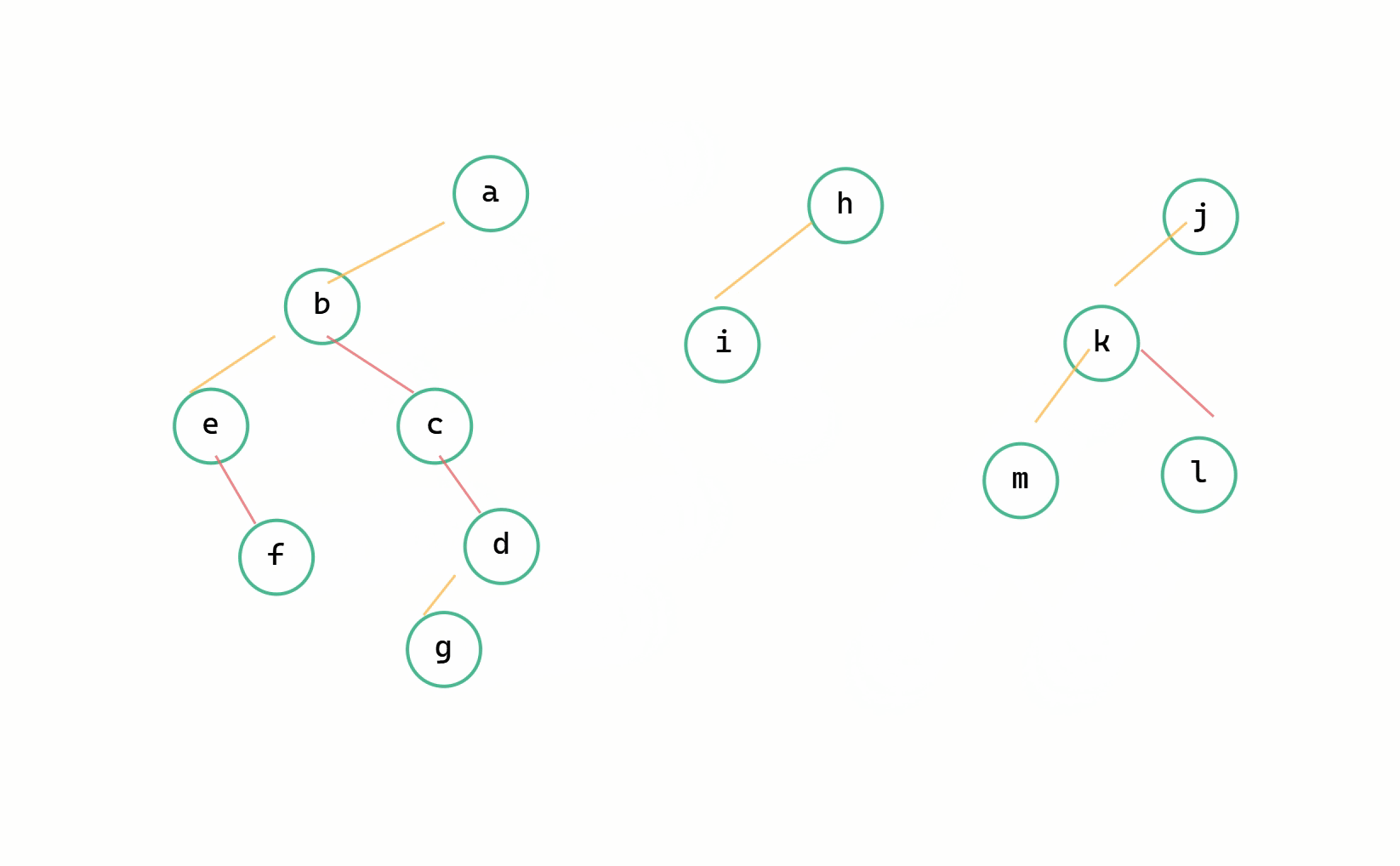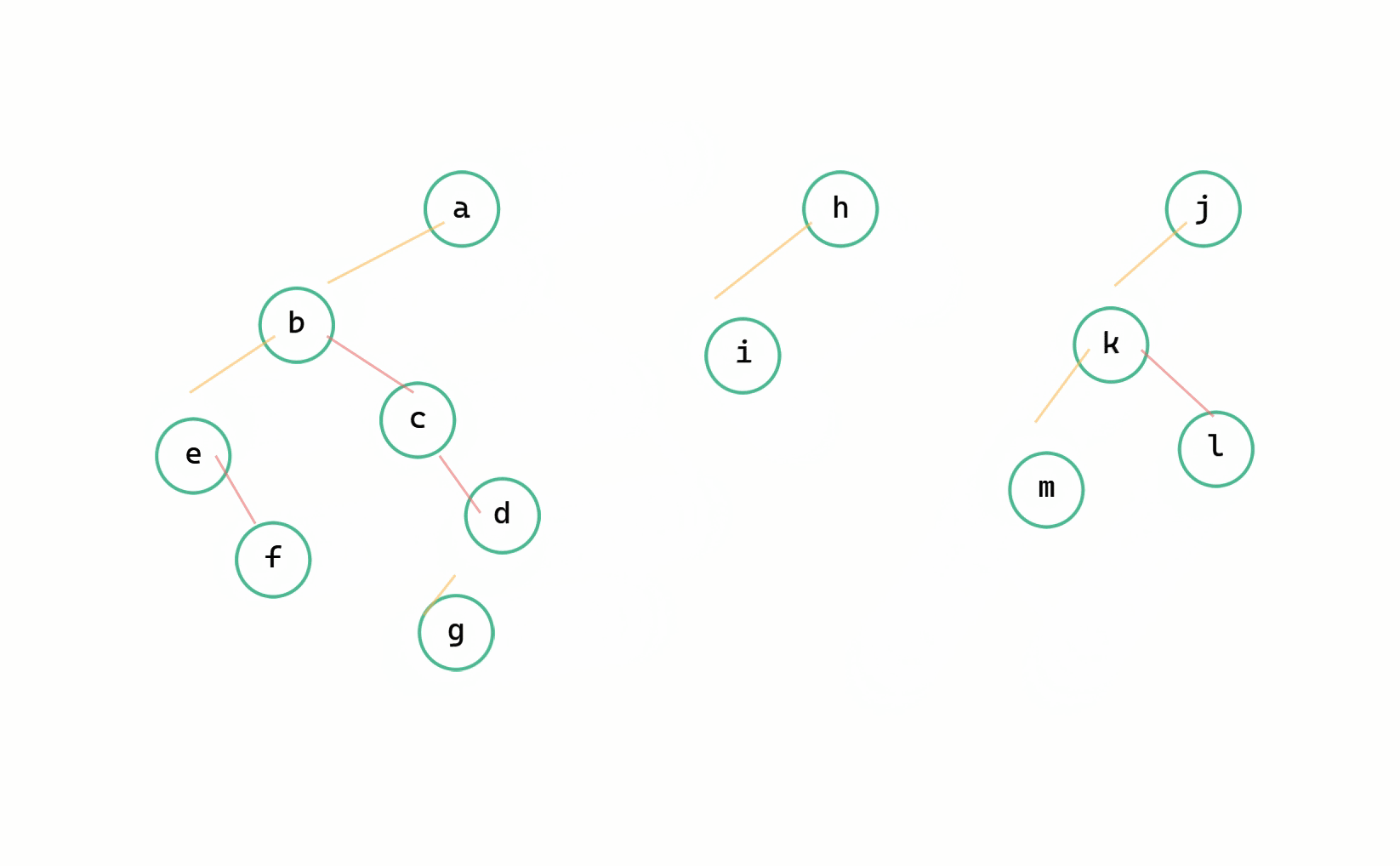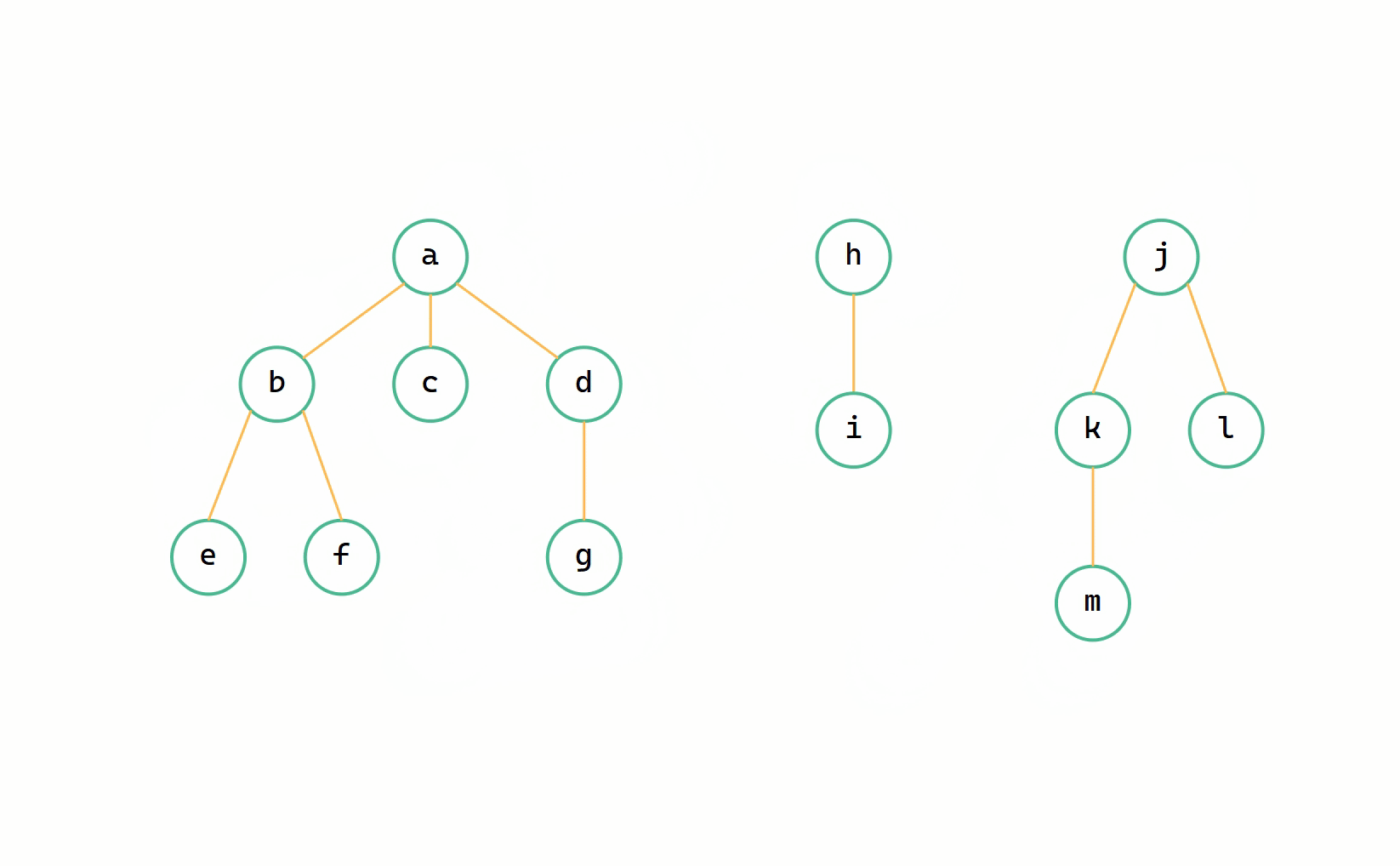
我們定義一個指標 p 從二元樹的根節點開始一直往右走，同時定義一個 q 來記錄要斷開的節點即 p->right ，依次將右孩子的連線斷開，由此將所有二元樹轉換為樹。

二元樹 --> 森林程式碼

//二元樹 轉化為 森林
Forest BinaryTree_Transform_to_Forest(BinaryTree bt){
    Forest F = (Forest)malloc(sizeof(forest));
    BinaryTree p = bt;	
    BinaryTree q = NULL;

    int count = 0;
    while(p){
        q = p->rightchild;    //q指向要切斷連線的下一個節點(即其右兒子)
        p->rightchild = NULL; //切斷連線 形成單獨的樹

        F->ct[count++] = BinaryTree_Transform_to_CSTree(p);//二元樹 轉化為 樹存到森林中
        p = q;    //p指向下一個節點 重複操作
    }

    F->n = count; //記錄森林中 樹的個數
    return F;
}

[資料結構] 樹、二元樹、森林的轉換

樹