前端演演算法之二分查詢

在陣列中查詢指定元素,如果存在就返回它的位置,如果不存在,就返回-1。

這是一道非常經典的演演算法題，考的就是二分查詢演演算法，首先分析二分查詢的思路：

假設一個陣列為 [3,5,19,22,25,33,45,47,57,66,71,78]（已經從小到大排好序），要求找出數值80的位置，如圖：

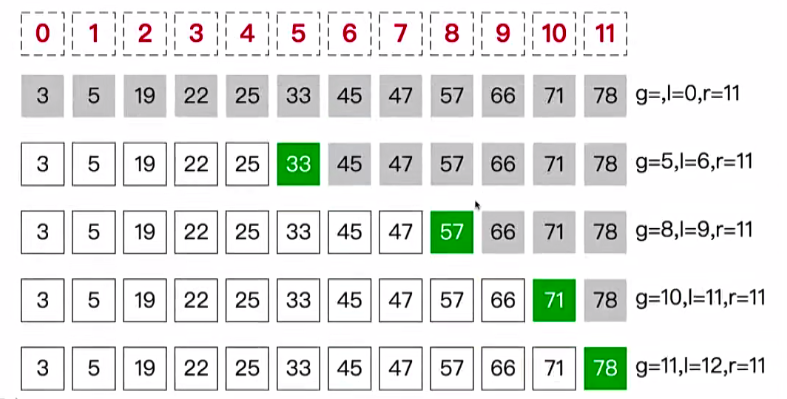
ps: g 為猜測數值的位置，l 為查詢的起點，r 為查詢的終點，灰色方格為查詢範圍

 步驟：

　　1.剛開始查詢範圍為整個陣列，第一次猜測數值是33，也就是猜測位置 g 為5，這個5是通過( l + r ) / 2 向下取整 得出的即（0 + 11）/ 2 = 5，由於當前數值為33，並不是目標數值80，且小於80，繼續向右查詢

　　2.第二次查詢，起點 l 為上一次猜測位置的下一位，即 l = 5 +1 = 6，r 還是為11，此次猜測位置 g 為（ l + r ）/ 2 = 8，對應數值為57，也小於80，繼續下一輪向右查詢

　　3.第三次查詢，起點 l 為上次猜測位置的下一位，即 l = 8 + 1 = 9，r 還是為11，此次猜測位置 g 為（ l + r ）/ 2 = 10，對應數值為71，也小於80，繼續下一輪向右查詢

　　4.第四次查詢，起點 l 為上次猜測位置的下一位，即 l = 10 + 1 = 11，r 還是為11，此次猜測位置 g 為（ l + r ）/ 2 = 11，對應數值為78，也小於80，繼續下一輪向右查詢

　　5.第五次查詢，起點 l 為上次猜測位置的下一位，即 l = 11 + 1 = 12，r 還是為11，此時 l > r ,查詢終止，且未找到目標數值，由於未找到80，所以應當返回-1。

其他條件不變，將目標值換成66，利用二分查詢找出對應數值的位置，如圖：

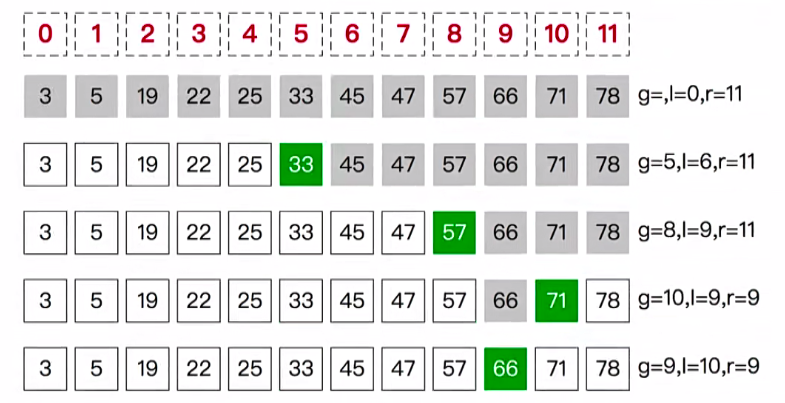
步驟：

　　1.剛開始查詢範圍為整個陣列，第一次猜測數值是33，也就是猜測位置 g 為5，這個5是通過( l + r ) / 2 向下取整 得出的即（0 + 11）/ 2 = 5，由於當前數值為33，並不是目標數值66，且小於66，繼續向右查詢

　　2.第二次查詢，起點 l 為上一次猜測位置的下一位，即 l = 5 + 1 = 6，r 還是為11，此次猜測位置 g 為（ l + r ）/ 2 = 8，對應數值為57，也小於66，繼續下一輪向右查詢

　　3.第三次查詢，起點 l 為上次猜測位置的下一位，即 l = 8 + 1 = 9，r 還是為11，此次猜測位置 g 為（ l + r ）/ 2 = 10，對應數值為71，由於71大於目標數值66，因此下一輪需向左查詢

　　4.第四次查詢，起點 l 不變，即 l = 9，r 為上次猜測位置 g 的上一位即9，由於 l 和 r 相同，所以該位置的數值為最後一個需要查詢的數值，不需要繼續猜測查詢了，而該數值也正好為目標數值66，因此返回目標數值66的位置為9。

通過以上分析，下面看看具體程式碼實現：

 1 function bsearch(A, x) {
 2     let l = 0, // 查詢範圍左邊界
 3       r = A.length - 1, // 查詢範圍右邊界
 4       g; // 猜測位置，即l,r中間的位置
 5     while (l <= r) {
 6       g = Math.floor((l + r) / 2); // 向下取整
 7       // 迴圈不變式
 8       if (A[g] === x) return g;
 9       else if (A[g] > x) r = g - 1;
10       else l = g + 1;
11     }
12     return -1;
13   }

測試結果：

腳踏實地行，海闊天空飛~