一、堆的基礎

1.1 優先佇列和堆

優先佇列（Priority Queue）：特殊的「佇列」，取出元素順序是按元素優先權（關鍵字）大小，而非元素進入佇列的先後順序。

若採用陣列或連結串列直接實現優先佇列，代價高。依靠陣列，基於完全二元樹結構實現優先佇列，即堆效率更高。一般來說堆代指二元堆積。

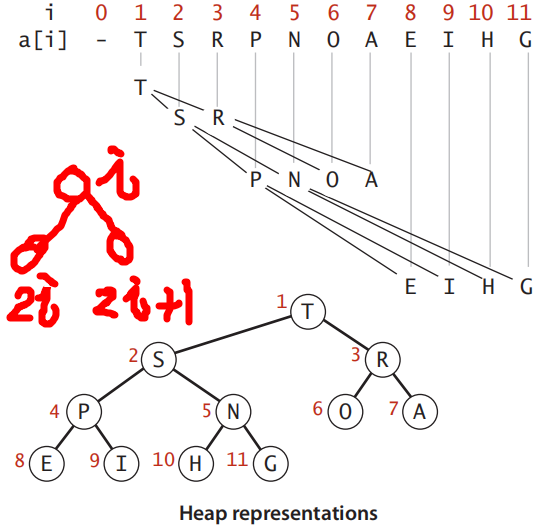
優先佇列的完全二元樹（堆）表示

1.2 堆

堆序性：父節點元素值比孩子節點大（小）

最大堆(MaxHeap), 也稱「大頂堆」：根節點為最大值；
最小堆(MinHeap), 也稱「小頂堆」：根節點為最小值。

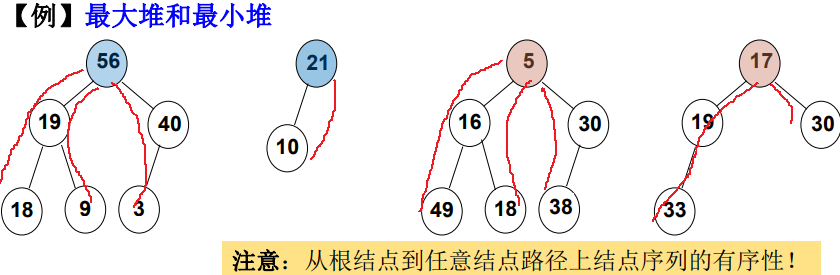
通常以最大堆為例。最小堆實現，直接把最大堆元素值取負。

二、最大堆實現

2.1 最大堆操作

最大堆（MaxHeap）資料結構實際為完全二元樹，每個結點的元素值不小於其子結點的元素值。

其主要操作有：

MaxHeap InitializeHeap( int MaxSize )：初始化一個空的最大堆。
Boolean IsFull( MaxHeap H )：判斷最大堆H是否已滿。
Boolean IsEmpty( MaxHeap H )：判斷最大堆H是否為空。
Insert( MaxHeap H, ElementType X )：將元素X插入最大堆H。
ElementType DeleteMax( MaxHeap H )：返回H中最大元素(高優先順序)。

核心操作為恢復堆序性：在堆中執行了可能違反堆序性的簡單修改後，需通過修改堆確保重新滿足堆序性。有兩種情況：

自底向上reheapify（上濾，swim）: 當某個節點的優先順序增加時（或在堆的底部新增一個新節點）時，必須向上遍歷調整堆以恢復堆序。
自頂向下reheapify（下濾, sink）：當節點優先順序減少（變小）時（例如，如果用鍵較小的新節點替換根上的節點），必須向下遍歷調整堆以恢復堆順。

可以先實現這兩個基本輔助操作，然後使用它們來實現插入和刪除最大值。其操作如下圖所示：

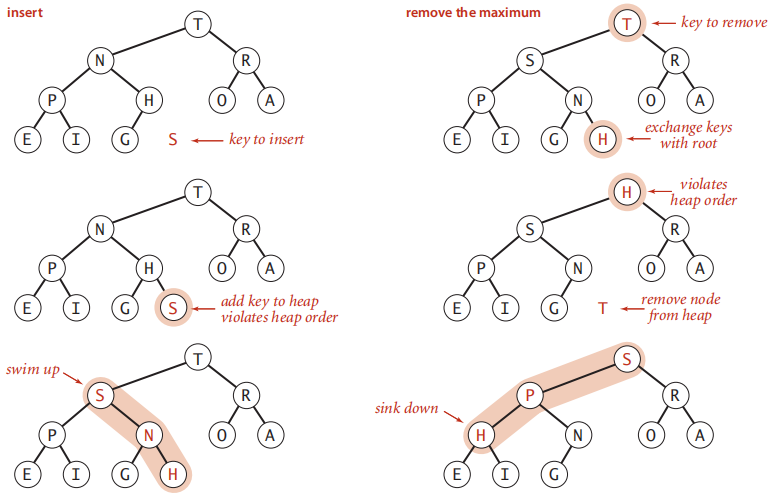
插入-插入元素索引上移，父節點值下移；

刪除-孩子節點值上移，末尾元素索引下移（降序插入排序，右邊有序，直到找到一個小於它的元素）；

2.2 最大堆C實現

2.2.1 基本操作

宣告堆結構

#include <stdlib.h>
#include <stdIo.h>
typedef int ElementType;
typedef struct HNode *Heap; /* 堆的型別定義 */
struct HNode {
    ElementType *Data; /* 儲存元素的陣列 */
    int Size;          /* 堆中當前元素個數 */
    int Capacity;      /* 堆的最大容量 */
};
typedef Heap MaxHeap; /* 最大堆 */
#define MAXDATA 1000000  /* 該值應根據具體情況定義為大於堆中所有可能元素的值 */

View Code

初始化堆

MaxHeap InitializeHeap( int MaxSize )
{   /* 建立容量為MaxSize的空的最大堆 */
 
    MaxHeap H = (MaxHeap)malloc(sizeof(struct HNode));
    /* 多一個元素存放"哨兵" */
    H->Data = (ElementType *)malloc((MaxSize+1)*sizeof(ElementType));  
    
    H->Size = 0;
    H->Capacity = MaxSize;
    H->Data[0] = MAXDATA;  /* 定義"哨兵"為大於堆中所有可能元素的值*/
 
    return H;
}

View Code

判是否滿堆，以及是否為空

bool IsFull( MaxHeap H )
{
    return (H->Size == H->Capacity);
}

bool IsEmpty( MaxHeap H )
{
    return (H->Size == 0);
}

View Code

2.2.2 最大堆的插入

將新增結點插入到，從其父結點到根結點的有序序列中 ( 完全二元樹，插入時間複雜度O(logN) ）

一步步往上調整（上濾）

void Insert( MaxHeap H, ElementType X )
{   /* 將元素X插入最大堆H，其中H->Data[0]已經定義為哨兵 */
    int i;
    /* 首先判斷，堆是否已滿。已滿則結束 */
    if ( IsFull(H) ) { 
        printf("最大堆已滿");
        return;
    }
      
    /* 若堆未滿，i指向堆末尾的下一個位置(空穴，當前size+1)，準備插入X */
    i = ++H->Size;  /* 類似插入排序，  */
    /* 若X 大於 其父節點值，則將父節點值下移至位置i， i位置(空穴）移到父節點位置[i/2] */
    for ( ; H->Data[i/2] < X; i /= 2 )
        H->Data[i] = H->Data[i/2]; /* 上濾X */
    
    H->Data[i] = X; /* 將X插入 */
    /* 若X是當前堆中最大元素，那麼會在堆頂時（比哨兵小）終止上移 */
}

View Code

2.2.3 最大堆的刪除

刪除位置-根結點，返回堆頂（最大值）元素，並調整堆使其保持堆序性（少了一個元素）。

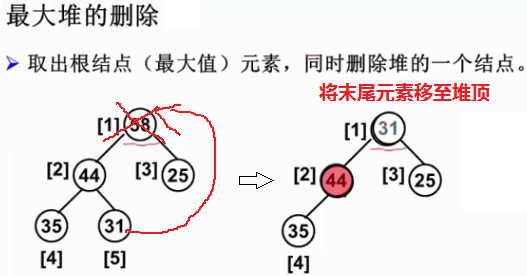
ElementType DeleteMax( MaxHeap H )
{   /* 從最大堆H中取出鍵值為最大的元素，並刪除一個結點 */
    int Parent, Child;   /* 指標 */
    ElementType MaxItem, X;    

    if ( IsEmpty(H) ) {
        printf("最大堆已為空"); /* 若堆已空，則結束（沒得刪） */
        return ERROR;
    }
 
    MaxItem = H->Data[1]; /* 取出根結點存放的最大值 */
    /* 用最大堆中最後一個元素X，從根結點開始，向上過濾下層結點 */
    X = H->Data[H->Size--]; /* 相當於刪掉末尾元素位置，故當前堆size要減1*/
    
    /* 迭代地將X和其更大的孩子節點值作比較，並調整位置（從根節點開始，給X找個位置） */
    /* Parent*2 <= H->Size判斷是否有左兒子(有無孩子)，若無則超出堆空間，跳出迴圈，直接把X放Parent */
    for ( Parent = 1; Parent*2 <= H->Size; Parent = Child ) {
        /* 找到當前更大的孩子節點*/
        Child = Parent * 2;  /* 令Child為左兒子，經過外層for迴圈判斷，Child只能 <= Parent */
        /* 若有右兒子((Child < H->Size))，則讓讓Child指向左右子結點的較大者 */
        if ( (Child != H->Size) && (H->Data[Child] < H->Data[Child+1]) )
            Child++; 
        /* 將末尾元素X和Child的值比較，若X >= Child值則結束（有序了）*/
        /* 若X < Child值 (Child更大)，則將Child值放在位置Parent，並將Parent位置移到Child位置 */
        if ( X >= H->Data[Child] ) 
            break;   /* 找到了合適位置 */
        else  /* Child元素上移，X移動到下一層（Parent = Child），繼續和其孩子節點比較 */
            H->Data[Parent] = H->Data[Child];
    }
    H->Data[Parent] = X;
 
    return MaxItem;
}

View Code

自頂向下，找到更大的孩子節點（孩子不一定是2個，也可能只有1個），並和末尾元素比較

若孩子更小或等於則不動，若孩子更大則將孩子值上移。末尾元素索引下移-下濾

2.2.4 最大堆的建立

將已經存在的N個元素，按最大堆的要求存放在一個一維陣列中

方法1：通過插入操作，將N個元素一個個相繼插入到一個初始為空的堆中去，其時間代價最大為O(N logN)。

方法2：線上性時間複雜度O(N)下，建立最大堆。

將N個元素按輸入順序存入，先滿足完全二元樹的結構特性
調整各結點位置，以滿足最大堆的有序特性

分析：該如何調整堆？

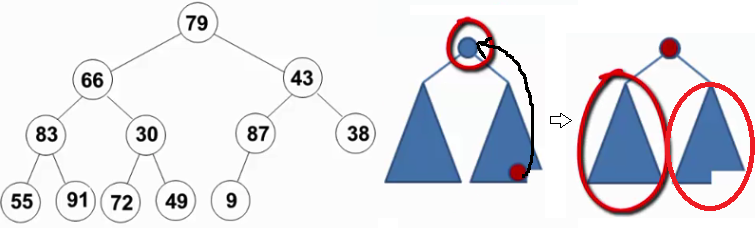
在刪除最大值操作中，末尾元素放置於堆頂，此時其左子樹和右子樹均為堆。其調整思路為，不斷地找更大的孩子調上來，自己下沉（下濾操作）。

但是，如上圖左子圖所示，初始化的堆並不滿足堆序性（對79而言，其左右均不是堆，其他節點也是這個情況），似乎不能直接使用刪除最大值操作。

實際可以逆向思維，找到最小滿足該情況的例子：

從倒數第一個有兒子的節點開始（末尾節點的父親，此節點的左右肯定是堆-葉節點），逆序執行（自底向上，逆層序遍歷）下濾操作。這樣當目標節點的左子樹和右子樹都為堆時，就可以自然地複用刪除最大值操作

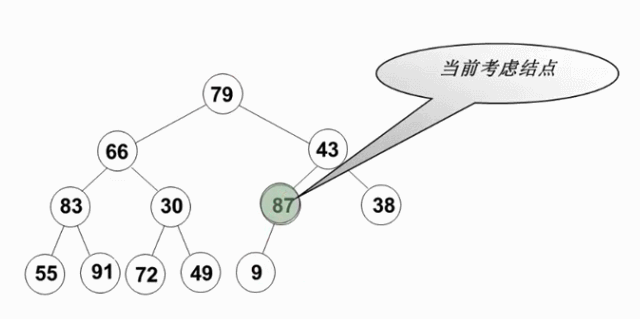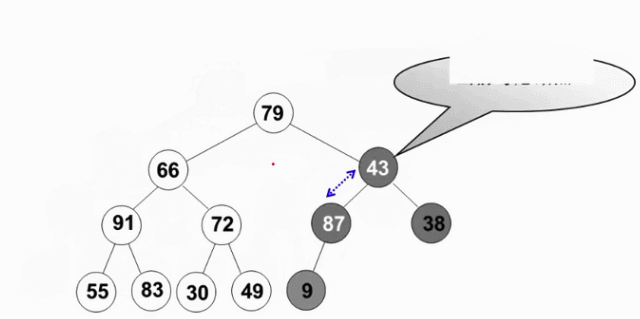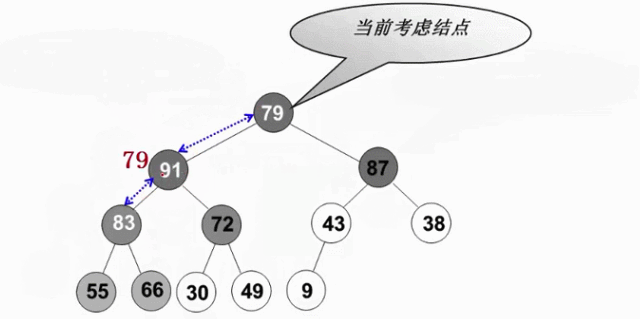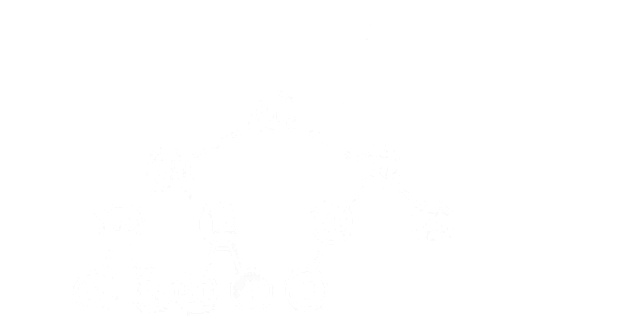
void PercolateDown( MaxHeap H, int p )
{   /* 下濾：將H中以H->Data[p]為根的子堆調整為最大堆 */
    int Parent, Child;
    ElementType X = H->Data[p]; /* 取出根結點存放的值 */
    for ( Parent=p; Parent*2<=H->Size; Parent=Child ) {
        Child = Parent * 2;
        if ( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) )
            Child++;  /* Child指向左右子結點的較大者 */
        if ( X >= H->Data[Child] )  break; /* 找到了合適位置 */
        else  /* 下濾X */
            H->Data[Parent] = H->Data[Child];
    }
    H->Data[Parent] = X;
}
 
void BuildHeap( MaxHeap H )
{   /* 調整H->Data[]中的元素，使滿足最大堆的有序性  */
    /* 這裡假設所有H->Size個元素已經存在H->Data[]中 */
 
    int i;
 
    /* 從最後一個結點的父節點開始，到根結點1 */
    for ( i = H->Size/2; i > 0; i-- )
        PercolateDown( H, i );
}

View Code

分析

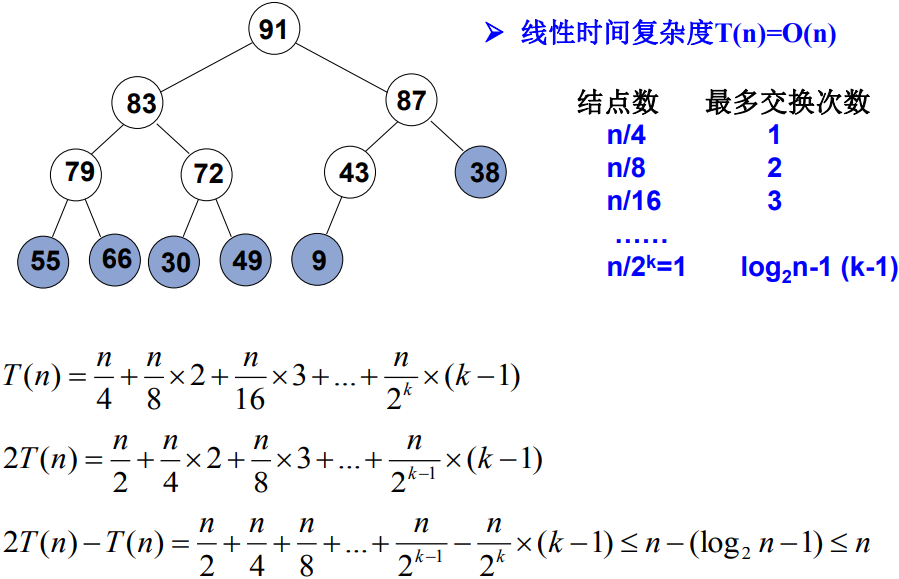
倒數第2層最多交換1次，其餘節點的交換次數此時按其深度線性遞增（節點數按2的對數下降）

基於下濾操作的刪除最大值實現：

ElementType DeleteMax( MaxHeap H )
{   /* 從最大堆H中取出鍵值為最大的元素，並刪除一個結點 */

    ElementType MaxItem = H->Data[1]; /* 取出根結點存放的最大值 */
  
    H->Data[1] = H->Data[H->Size--]   /* 取出根結點存放的最大值 */
  
    PercolateDown(H, 1);  /* 從根結點開始，向上過濾下層結點（末尾節點下濾） */
    return MaxItem;
}

View Code

可知，刪除最大值中的調整操作是BuildHeap的特例。此外，還有刪除堆中某個元素、增大某個元素的優先順序和減小某個元素的優先順序的操作。高效執行此操作的前提，是用雜湊表簡歷key到index的對映。

2.3 最大堆Python實現

邏輯參照上述C語言版

class Heap:
    def __init__(self, n):
        self.capacity = n
        self.size = 0
        self.arr = [None] * (self.capacity+1)
        self.arr[0] = 2e24

    def insert(self, num): 
        if self.size == self.capacity:
            print("Out of size")
        else:
            self.size += 1
            child = self.size  # 空穴位置
            # 上濾, 當左兒子在堆範圍內
            while num > self.arr[child // 2]:
                parent = child // 2
                self.arr[child] = self.arr[parent]
                child = parent

            self.arr[child] = num

    def pop(self): 
        if self.size == 0:
            print("Empty")
        else:
            max_item = self.arr[1] # 取堆頂
            x = self.arr[self.size] # 取堆末尾元素
            self.size -= 1

            parent = 1
            # 下濾, 當左兒子在堆範圍內
            while parent * 2  <= self.size:
                child = parent * 2 
                if child != self.size and self.arr[child+1] > self.arr[child]:
                    child += 1
                if self.arr[child] > x:
                    self.arr[parent] = self.arr[child] # 孩子節點值上移
                    parent = child
                else:
                    break
            self.arr[parent] = x
            return max_item

View Code

呼叫python包

import queue
, random

class Heap():
    def __init__(self, k):
        if k > 0:
            self.q = queue.PriorityQueue(k)

    def queue(self):
        return self.q.queue
        
    def enque(self, key):
        # 當前堆大小小於其容量 
        if self.q._qsize() < self.q.maxsize:
            self.q.put(key)
        else:
            self.q.get() # 刪除堆頂 
            self.q.put(key)

    def deque(self):
        if not self.q.empty():
            return self.q.get()
        else:
            print("Empty heap")


h1 = Heap(10)
for i in range(15):
    h1.enque(i)


print(h1.queue())  # 最小堆，k  可得到堆排序得到最大的k個 

l1 = [ random.randint(1, 100) for i in range(20)]
print(l1)

for i in l1:
    h1.enque(i)
    
print(h1.queue())
print("\nPriority Queue:")
print([h1.deque() for i in range(h1.q._qsize())])

View Code

三、堆的應用

經典的應用有選擇問題、堆排序和Huffman編碼等等。

3.1. 選擇問題

問題描述：輸入N個數，找到第k個最大的數。如果K=N/2，就是找中位數，這是選擇問題的最困難的情況。

暴力法：直接排序，並返回排序陣列的倒數第K個數，O(NlogN)，

使用堆：

演演算法A: 大優先佇列

將N個元素讀入陣列，並構建最大堆O(N)
然後執行K次刪除最大元素O(KlogN)

最後一次刪除的元素就是第K個最大值，總時間複雜度：O(N + KlogN)。

如果k小時，執行時間取決於建堆O(N)。
如果k大時，執行時間取決於刪除O(KlogN)。例如K=N，即O(NlogN)，直接堆排序
如果K=N/2，平均時間複雜度(NlogN)

演演算法B: 小優先佇列（流式處理）

將K個元素讀入陣列，並構建最小堆O(K)
依次刪除最小堆的最小元素，再將元素插入最小堆（把待插入元素放在堆頂，然後下濾）O((N-K)logK)

因此，O(K + (N-K)logK) = O(K(1-logK) + NlogK) = O(NlogK)

3.2 堆排序

將N個元素讀入陣列，並構建最大堆O(N) Heap的原理和實現
然後，執行N-1次刪除最大元素O(NlogN)，返回的元素構成的陣列有序

每次刪除元素可以放在當前堆尾。慢於希爾排序。

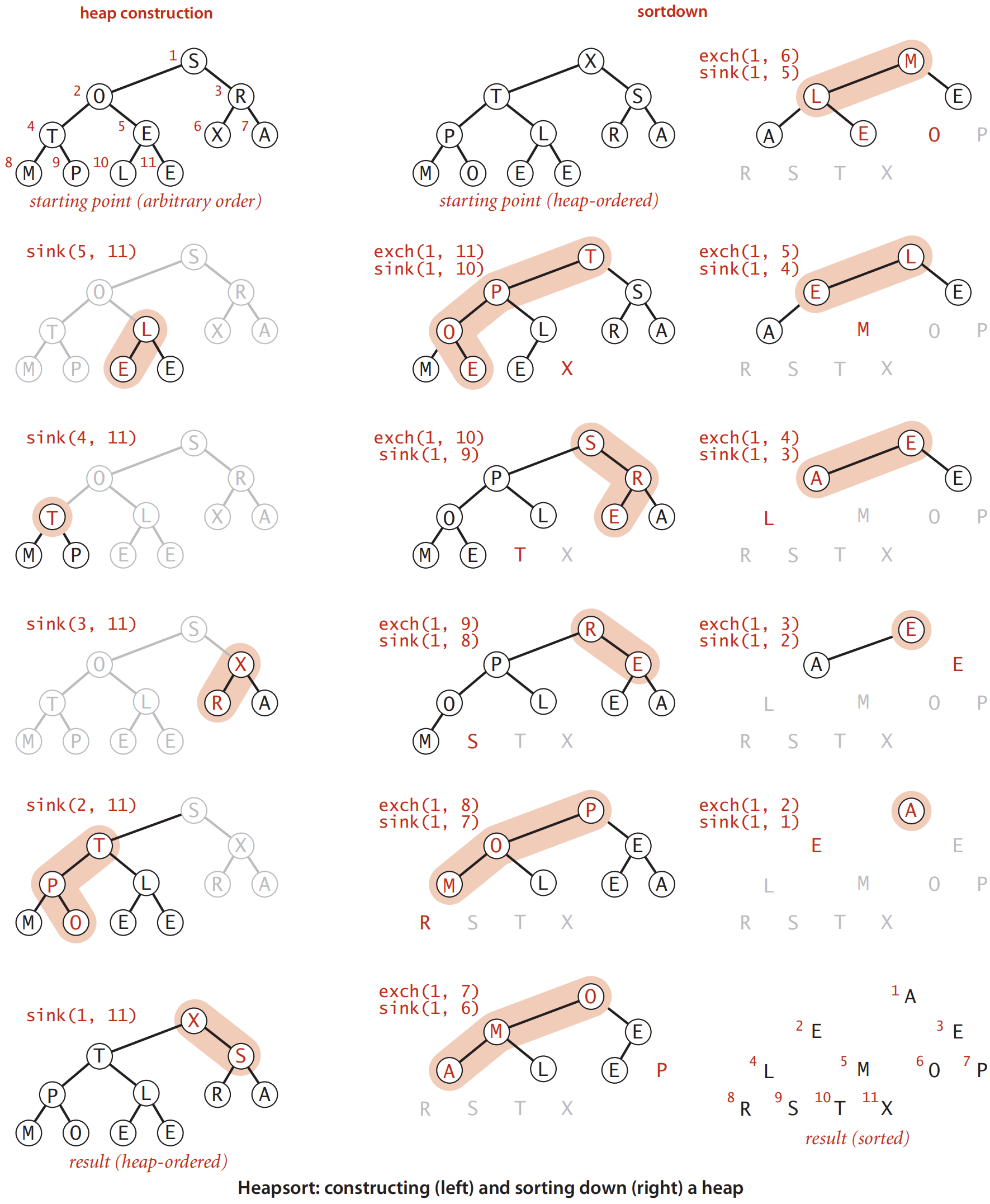
實際實現時，先自底向上呼叫N/2 + 1次下濾操作PercolateDown，線性建堆。
然後，每次把堆頂元素和堆末尾元素交換，將堆size減1，並從根節點執行下濾操作PercolateDown。共計N-1次（最後一個元素已經在堆頂，不需要操作）

堆排序不完全同於二元堆積的刪除，其陣列元素初始位置在0，所以下濾開始位置為0而不是1，下濾範圍從N-1到1（實際堆的大小）。

Python調包版

def sortArray(nums: List[int]) -> List[int]:
    import heapq
    heapq.heapify(nums)
    return [heapq.heappop(nums) for i in range(len(nums))]

View Code

Python實現

class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        def heapify(nums, parent, arr_size): 
            # parent為開始下濾節點索引，p為當前堆大小(決定調整邊界)
            x = nums[parent]
            # 下濾, 當左兒子在堆範圍內
            while parent * 2 + 1 < arr_size:
                child = parent * 2 + 1
                if child != arr_size-1 and nums[child+1] > nums[child]:
                    child += 1
                if nums[child] > x:
                    nums[parent] = nums[child]
                    parent = child
                else:
                    break
            nums[parent] = x
            
        # 構建堆
        n = len(nums)
        for i in range(n//2, -1, -1):
            heapify(nums, i, n)  # 建堆時堆大小固定為其容量
        # 迭代刪除堆頂元素
        for i in range(n-1, 0, -1):
            # 將堆頂元素取出（直接在末尾儲存），把末尾元素放堆頂
            nums[i], nums[0] = nums[0], nums[i]
            heapify(nums, 0, i) # 然後下濾
        return nums

View Code

C實現

void PercolateDown( ElementType A[], int p, int N )
{
   /* 將N個元素的陣列中以A[p]為根的子堆調整為最大堆 */
    int Parent, Child;
    ElementType X = A[p]; /* 取出根結點存放的值 */
    for ( Parent=p; (Parent*2+1) < N; Parent=Child ) {
        Child = Parent * 2 + 1;
        if ( (Child != N-1) && (A[Child] < A[Child+1]) )
            Child++;  /* Child指向左右子結點的較大者 */
        if ( X >= A[Child] ) break; /* 找到了合適位置 */
        else  /* 下濾X */
            A[Parent] = A[Child];
    }
    A[Parent] = X;
}

void HeapSort( ElementType A[], int N ) 
{ 
     int i;       
     /* 建立最大堆 */
     for ( i = N/2-1; i >= 0; i-- )
         PercolateDown( A, i, N );
      
     for ( i=N-1; i>0; i-- ) {
         /* 刪除最大堆頂 */
         Swap( &A[0], &A[i] ); 
         PercolateDown( A, 0, i );
     }
}

View Code

參考資料：演演算法第四版，浙江大學-資料結構慕課

資料結構-詳解優先佇列的二元堆積（最大堆）原理、實現和應用-C和Python

一、堆的基礎

1.1 優先佇列和堆

1.2 堆

二、最大堆實現

2.1 最大堆操作

2.2 最大堆C實現

2.2.1 基本操作

2.2.2 最大堆的插入

2.2.3 最大堆的刪除

2.2.4 最大堆的建立

2.3 最大堆Python實現

三、堆的應用

3.1. 選擇問題

3.2 堆排序