從設計110序列檢測器來看--同步時序電路設計

開學臨近，本人查缺補漏，應對推遲的期末考試
同步時序邏輯設計，難度有所增加，本人慾通過110序列檢測器來解決這一問題點：

設計步驟：

1.獲取原始狀態圖與狀態表--分析狀態圖表
2.最簡化狀態圖表
3.狀態編碼
4.利用狀態轉移表與觸發器特徵設計觸發器激勵
5.卡諾圖化簡
6.電路實現
7.檢查無關項

具體操作

獲取原始狀態圖與狀態表--分析狀態圖表

狀態設定:
s₀ --->初態：表示接收一位資料「0」
s₁ --->「1」
s₂ --->"11"
s₃ --->"110" 此時輸出 z = 1；其他情況 z = 0
分析狀態轉換情況：

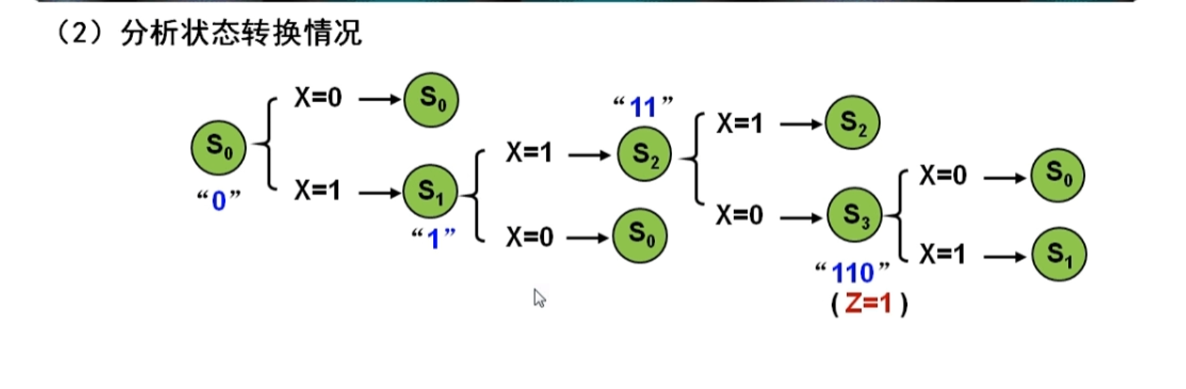
原式狀態圖如下:

graph TB S0 --->|X=0,Z=0| S0 S0 --->|X=1,Z=0| S1 S1 --->|X=0,Z=0|S0 S1 --->|X=1,Z=0|S2 S2 --->|X=1,Z=0|S2 S2 --->|X=0,Z=1|S3{S3 此時z=1} S3 --->|X=1,Z=0|S1 S2 --->|X=1,Z=0|S0

手寫版：

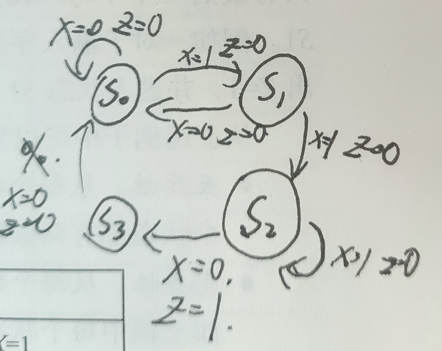
原始狀態表:

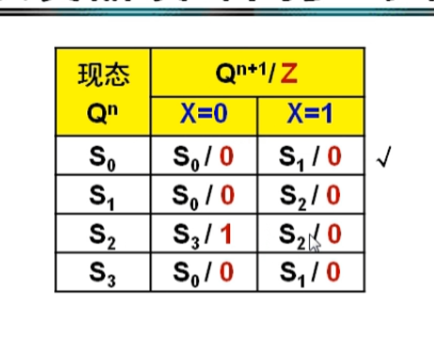
對其進行化簡

發現s3與s0相同,刪去s3

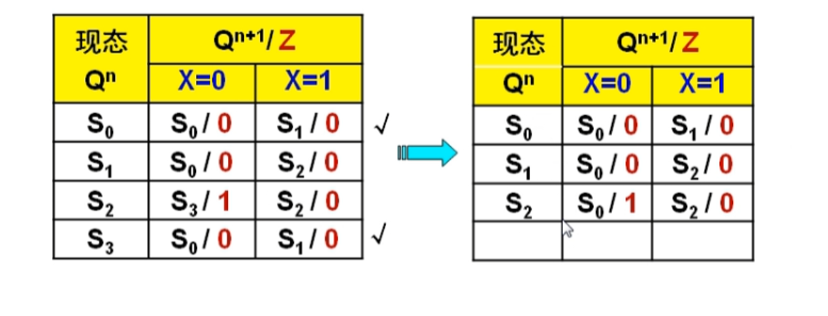
狀態分配

有s0,s1,s2三種狀態,所以要使用兩個JK觸發器或者D觸發器
我們先以JK觸發器為例:

設定編碼

~~~
                   y2   y1
s0------------>    0    0
s1------------->   1    0
s2------------->   1    1
y1,y2分別為兩個jk觸發器的Q輸出
~~~

列真值表

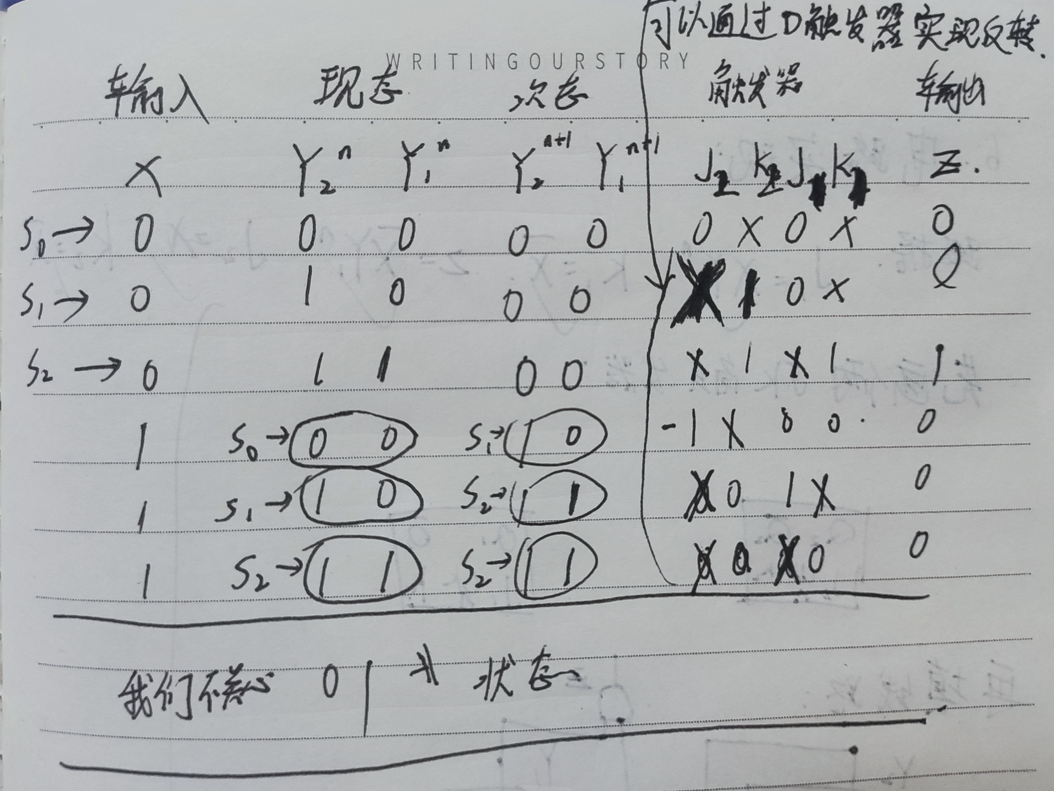
利用JK觸發器的特性，可寫出J2,K2,J1,K1的高低電壓情況，使y2，y1從現態變成次態

此真值表中的觸發器的取值就是將現態轉變為次態的J,K取值情況

JK觸發器特性
J = K = 0 ---> D = Q ,保持
J = 0,K = 1 ---> D = 0,復位
J = 1,K = 0 ---> D = 1 ,置位
J = K = 1 ----> D = \(\bar{Q}\) ，反轉，此時可以認為就是T觸發器的效果

利用卡諾圖化簡：

要畫五個卡諾圖，分別是：J2,K2,J1,K1,Z

** 根據真值表中的值來畫卡諾圖**

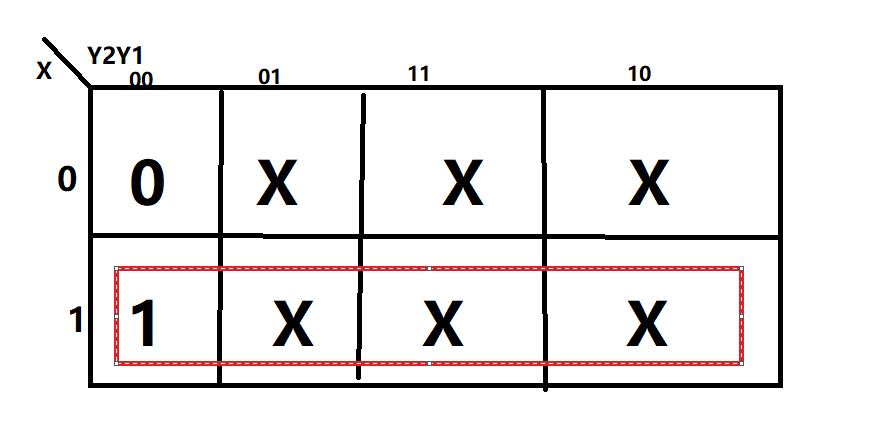
可得：J2 = X

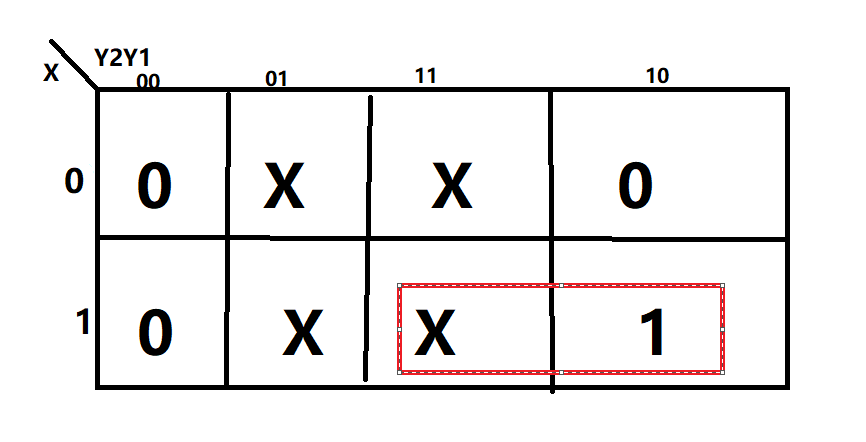
可得： J1 = X·Y2

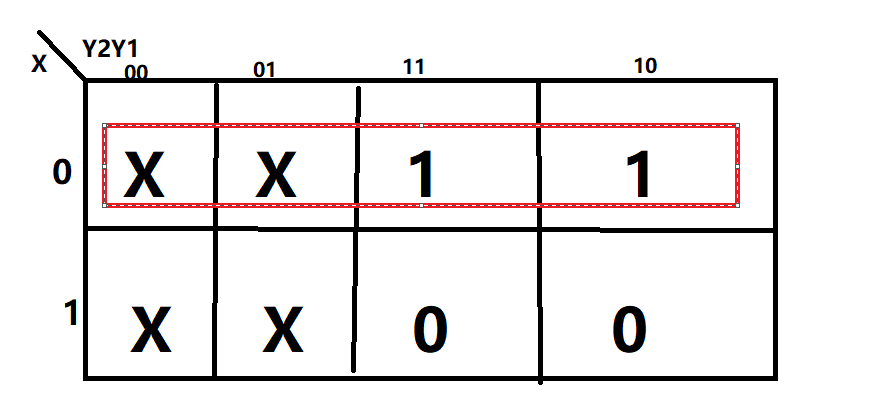
K2= \(\bar{X}\)

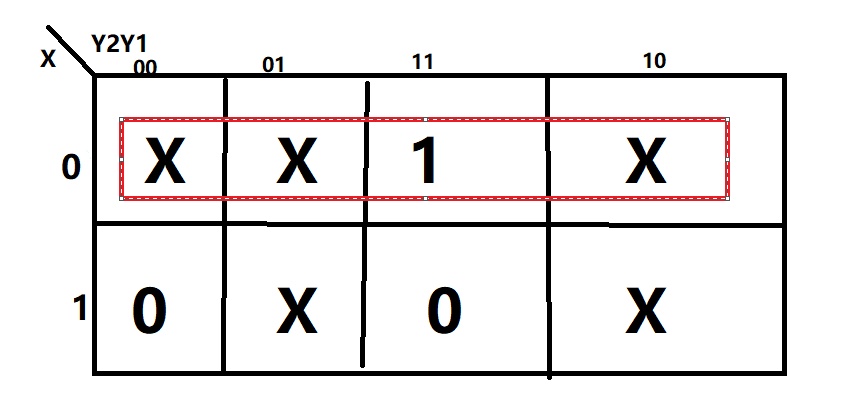
K1 = \(\bar{X}\)

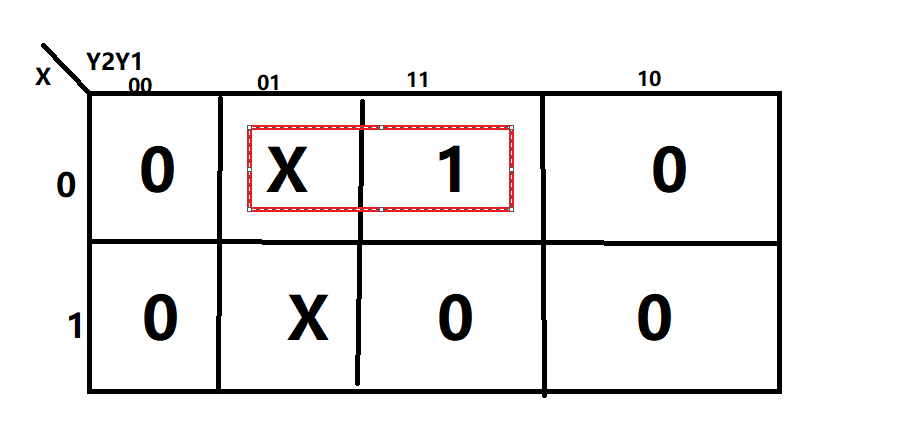
Z = \(\bar{X}\)·Y1

電路實現

根據：J2 = X， J1 = XY2，K2= \(\bar{X}\)，K1 = \(\bar{X}\)，Z = \(\bar{X}\)*Y1來畫電路

X為一個輸入引腳，Z為輸出引腳\

先畫倆JK觸發器：

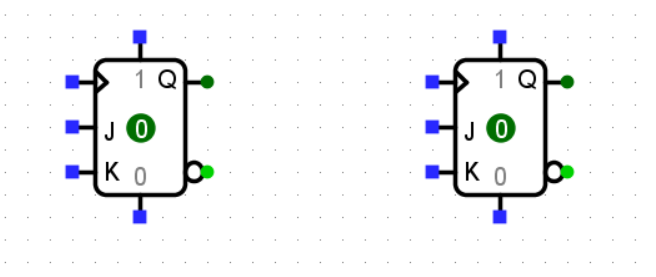
再添電路：

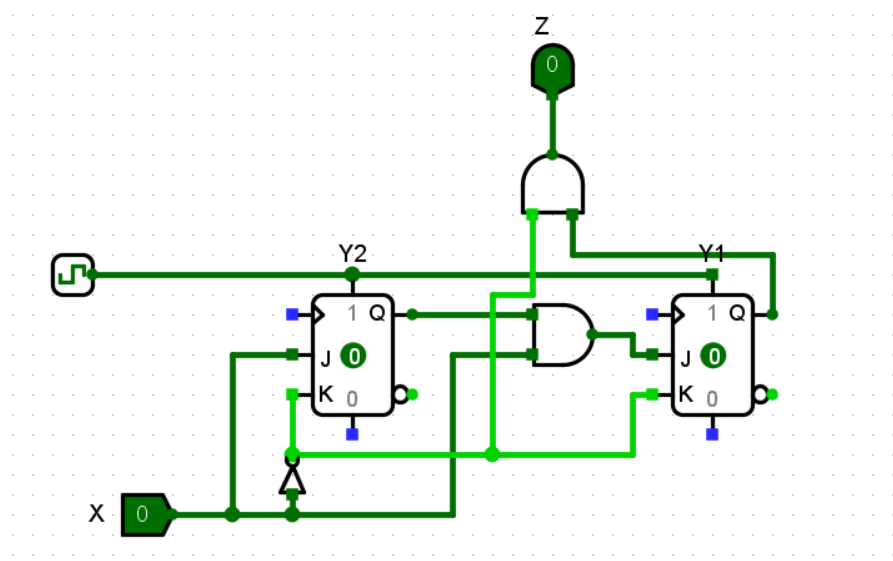
檢查無關項

思路：將未用到的「01」狀態帶入計算

利用JK觸發器的次態方程 D = J\(\bar{Q}\) + \(\bar{K}\)Q
得： Y₁ⁿ⁺¹ = J₁\(\bar{Y}\)₁ⁿ + \(\bar{K}\)₁Y₁ⁿ = XY₂ⁿ\(\bar{Y}\)₁ⁿ + XY₁ⁿ = X(Y₁ⁿ + Y₂ⁿ)
Y₂ⁿ⁺¹ = X\(\bar{Y}\)₂ⁿ + XY₂ⁿ = X

Y₁
現在再將「 Y₂ = 0, Y₁= 1」帶入

graph TB 01 --->|情況1:X = 0|00{滿足情況s0,可以自啟動} 01 --->|情況2:X = 1|11{滿足情況s2,可以自啟動}

情況1：
Y₂ⁿ⁺¹ = 0

Y₁ⁿ⁺¹ = 0(1+0) = 0

情況2;
Y₂ⁿ⁺¹ = 1(1+0) = 1
Y₁ⁿ⁺¹ = 1

檢查無誤，電路可以自啟動，自此也就完成了

結尾補充

補充：
對於未用狀態得2輸出設定調整：可以將其輸出調整為無效即可
對於未用狀態的次態設定調整：可以將未用狀態的次態設定成初態或其編碼最接近的工作狀態 --例如：假設本題中的「01」未用狀態，則可將其次態設定為「00」或「11」，這樣列真值表時把他也考慮在內，在列卡諾圖……等一系列操作

各位也可以根據這個思路，把JK觸發器換成T觸發器，總體步驟不變，列真值表時把jk換成T ，利用次態是否反轉判斷T的取值，列卡諾圖……