技術文章 » 一文帶你入門圖機器學習

一文帶你入門圖機器學習

2023-01-29 15:01:19

本文主要涉及圖機器學習的基礎知識。

我們首先學習什麼是圖，為什麼使用圖，以及如何最佳地表示圖。然後，我們簡要介紹大家如何在圖資料上學習，從神經網路以前的方法 (同時我們會探索圖特徵) 到現在廣為人知的圖神經網路 (Graph Neural Network，GNN)。最後，我們將一窺圖資料上的 Transformers 世界。

什麼是圖？

本質上來講，圖描述了由關係互相連結起來的實體。

現實中有很多圖的例子，包括社群網路 (如推特，長毛象，以及任何連結論文和作者的參照網路) 、分子、知識圖譜 (如 UML 圖，百科全書，以及那些頁面之間有超連結的網站) 、被表示成句法樹的句子、3D 網格等等。因此，可以毫不誇張地講，圖無處不在。

圖 (或網路) 中的實體稱為 節點 (或頂點) ，它們之間的連線稱為 邊 (或連結) 。舉個例子，在社群網路中，節點是使用者，而邊是他 (她) 們之間的連線關係；在分子中，節點是原子，而邊是它們之間的分子鍵。

  • 可以存在不止一種型別的節點或邊的圖稱為 異構圖 (heterogeneous graph) (例子：參照網路的節點有論文和作者兩種型別，含有多種關係型別的 XML 圖的邊是多型別的) 。異構圖不能僅由其拓撲結構來表徵，它需要額外的資訊。本文主要討論同構圖 (homogeneous graph) 。

  • 圖還可以是 有向 (directed) 的 (如一個關注網路中，A 關注了 B，但 B 可以不關注 A) 或者是 無向 (undirected) 的 (如一個分子中，原子間的關係是雙向的) 。邊可以連線不同的節點，也可以自己連線自己 (自連邊，self-edges) ，但不是所有的節點都必須有連線。

如果你想使用自己的資料，首先你必須考慮如何最佳地刻畫它 (同構 / 異構，有向 / 無向等) 。

圖有什麼用途？

我們一起看看在圖上我們可以做哪些任務吧。

在 圖層面，主要的任務有：

  • 圖生成，可在藥物發現任務中用於生成新的可能的藥物分子，
  • 圖演化 (給定一個圖，預測它會如何隨時間演化) ，可在物理學中用於預測系統的演化，
  • 圖層面預測 (基於圖的分類或迴歸任務) ，如預測分子毒性。

在 節點層面，通常用於預測節點屬性。舉個例子，Alphafold 使用節點屬性預測方法，在給定分子總體圖的條件下預測原子的 3D 座標，並由此預測分子在 3D 空間中如何摺疊，這是個比較難的生物化學問題。

在 邊層面，我們可以做邊屬性預測或缺失邊預測。邊屬性預測可用於在給定藥物對 (pair) 的條件下預測藥物的不良副作用。缺失邊預測被用於在推薦系統中預測圖中的兩個節點是否相關。

另一種可能的工作是在 子圖層面 的，可用於社群檢測或子圖屬性預測。社群網路用社群檢測確定人們之間如何連線。我們可以在行程系統 (如 Google Maps) 中發現子圖屬性預測的身影，它被用於預測到達時間。

完成這些任務有兩種方式。

當你想要預測特定圖的演化時，你工作在 直推 (transductive) 模式，直推模式中所有的訓練、驗證和推理都是基於同一張圖。如果這是你的設定，要多加小心！在同一張圖上建立訓練 / 評估 / 測試集可不容易。 然而，很多工其實是工作在不同的圖上的 (不同的訓練 / 評估 / 測試集劃分) ，我們稱之為 歸納 (inductive) 模式。

如何表示圖？

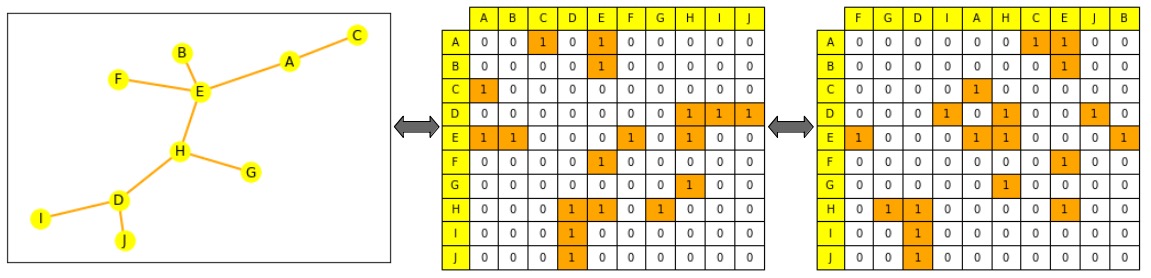
常用的表示圖以用於後續處理和操作的方法有 2 種：

  • 表示成所有邊的集合 (很有可能也會加上所有節點的集合用以補充) 。
  • 或表示成所有節點間的鄰接矩陣。鄰接矩陣是一個 $node_size \times node_size$ 大小的方陣，它指明圖上哪些節點間是直接相連的 (若 $n_i$ 和 $n_j$ 相連則 $A_{ij} = 1$，否則為 0) 。

注意：多數圖的邊連線並不稠密，因此它們的鄰接矩陣是稀疏的，這個會讓計算變得困難。

雖然這些表示看上去很熟悉，但可別被騙了！

圖與機器學習中使用的典型物件大不相同，因為它們的拓撲結構比序列 (如文字或音訊) 或有序網格 (如影象和視訊) 複雜得多：即使它們可以被表示成連結串列或者矩陣，但它們並不能被當作有序物件來處理。

這究竟意味著什麼呢？如果你有一個句子，你交換了這個句子的詞序，你就創造了一個新句子。如果你有一張影象，然後你重排了這個影象的列，你就創造了一張新影象。

但圖並不會如此。如果你重排了圖的邊列表或者鄰接矩陣的列，圖還是同一個圖 (一個更正式的叫法是置換不變性 (permutation invariance) ) 。

基於機器學習的圖表示

使用機器學習處理圖的一般流程是：首先為你感興趣的物件 (根據你的任務，可以是節點、邊或是全圖) 生成一個有意義的表示，然後使用它們訓練一個目標任務的預測器。與其他模態資料一樣，我們想要對這些物件的數學表示施加一些約束，使得相似的物件在數學上是相近的。然而，這種相似性在圖機器學習上很難嚴格定義，舉個例子，具有相同標籤的兩個節點和具有相同鄰居的兩個節點哪兩個更相似？

注意：在隨後的部分，我們將聚焦於如何生成節點的表示。一旦你有了節點層面的表示，就有可能獲得邊或圖層面的資訊。你可以通過把邊所連線的兩個節點的表示串聯起來或者做一個點積來得到邊層面的資訊。至於圖層面的資訊，可以通過對圖上所有節點的表示串聯起來的張量做一個全域性池化 (平均，求和等) 來獲得。當然，這麼做會平滑掉或丟失掉整圖上的一些資訊，使用迭代的分層池化可能更合理，或者增加一個連線到圖上所有其他節點的虛擬節點，然後使用它的表示作為整圖的表示。

神經網路以前的方法

只使用手工設計特徵

在神經網路出現之前，圖以及圖中的感興趣項可以被表示成特徵的組合，這些特徵組合是針對特定任務的。儘管現在存在 更復雜的特徵生成方法，這些特徵仍然被用於資料增強和 半監督學習。這時，你主要的工作是根據目標任務，找到最佳的用於後續網路訓練的特徵。

節點層面特徵 可以提供關於其重要性 (該節點對於圖有多重要？) 以及 / 或結構性 (節點周圍的圖的形狀如何？) 資訊，兩者可以結合。

節點 中心性 (centrality) 度量圖中節點的重要性。它可以遞迴計算，即不斷對每個節點的鄰節點的中心性求和直到收斂，也可以通過計算節點間的最短距離來獲得，等等。節點的 度 (degree) 度量節點的直接鄰居的數量。聚類係數 (clustering coefficient) 度量一個節點的鄰節點之間相互連線的程度。圖元度向量 (Graphlets degree vectors，GDV) 計算給定根節點的不同圖元的數目，這裡圖元是指給定數目的連通節點可建立的所有迷你圖 (如：3 個連通節點可以生成一個有兩條邊的線，或者一個 3 條邊的三角形) 。

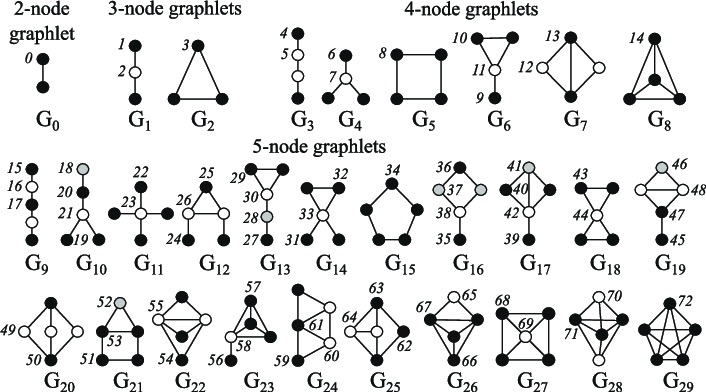
邊層面特徵帶來了關於節點間連通性的更多細節資訊，有效地補充了圖的表示，有：兩節點間的 最短距離 (shortest distance)，它們的公共鄰居 (common neighbours)，以及它們的 卡茲指數 (Katz index) (表示兩節點間從所有長度小於某個值的路徑的數目，它可以由鄰接矩陣直接算得) 。

圖層面特徵 包含了關於圖相似性和規格的高層資訊。總 圖元數 儘管計算上很昂貴，但提供了關於子圖形狀的資訊。核方法 通過不同的 「節點袋 (bag of nodes) 」 (類似於詞袋 (bag of words) ) 方法度量圖之間的相似性。

基於遊走的方法

基於遊走的方法 使用在隨機遊走時從節點j存取節點i的可能性來定義相似矩陣；這些方法結合了區域性和全域性的資訊。舉個例子，Node2Vec模擬圖中節點間的隨機遊走，把這些遊走路徑建模成跳字 (skip-gram) ，這與我們處理句子中的詞很相似，然後計算嵌入。基於隨機遊走的方法也可被用於加速 Page Rank方法，幫助計算每個節點的重要性得分 (舉個例子：如果重要性得分是基於每個節點與其他節點的連通度的話，我們可以用隨機遊走存取到每個節點的頻率來模擬這個連通度) 。

然而，這些方法也有限制：它們不能得到新的節點的嵌入向量，不能很好地捕獲節點間的結構相似性，也使用不了新加入的特徵。

圖神經網路

神經網路可泛化至未見資料。我們在上文已經提到了一些圖表示的約束，那麼一個好的神經網路應該有哪些特性呢？

它應該：

  • 滿足置換不變性：

    • 等式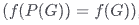：，這裡 f 是神經網路，P 是置換函數，G 是圖。
    • 解釋：置換後的圖和原圖經過同樣的神經網路後，其表示應該是相同的。

  • 滿足置換等價性

    • 公式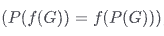：，同樣 f 是神經網路，P 是置換函數，G 是圖。
    • 解釋：先置換圖再傳給神經網路和對神經網路的輸出圖表示進行置換是等價的。

典型的神經網路，如迴圈神經網路 (RNN) 或折積神經網路 (CNN) 並不是置換不變的。因此，圖神經網路 (Graph Neural Network, GNN) 作為新的架構被引入來解決這一問題 (最初是作為狀態機使用) 。

一個 GNN 由連續的層組成。一個 GNN 層通過 訊息傳遞 (message passing) 過程把一個節點表示成其鄰節點及其自身表示的組合 (聚合 (aggregation)) ，然後通常我們還會使用一個啟用函數去增加一些非線性。

與其他模型相比：CNN 可以看作一個鄰域 (即滑動視窗) 大小和順序固定的 GNN，也就是說 CNN 不是置換等價的。一個沒有位置嵌入 (positional embedding) 的 Transformer 模型可以被看作一個工作在全連線的輸入圖上的 GNN。

聚合與訊息傳遞

多種方式可用於聚合鄰節點的訊息，舉例來講，有求和，取平均等。一些值得關注的工作有：

  • 圖折積網路 對目標節點的所有鄰節點的歸一化表示取平均來做聚合 (大多數 GNN 其實是 GCN) ；
  • 圖注意力網路 會學習如何根據鄰節點的重要性不同來加權聚合鄰節點 (與 transformer 模型想法相似) ；
  • GraphSAGE 先在不同的跳數上進行鄰節點取樣，然後基於取樣的子圖分多步用最大池化 (max pooling) 方法聚合資訊；
  • 圖同構網路 先計算對鄰節點的表示求和，然後再送入一個 MLP 來計算最終的聚合資訊。

選擇聚合方法：一些聚合技術 (尤其是均值池化和最大池化) 在遇到在鄰節點上僅有些微差別的相似節點的情況下可能會失敗 (舉個例子：採用均值池化，一個節點有 4 個鄰節點，分別表示為 1，1，-1，-1，取均值後變成 0；而另一個節點有 3 個鄰節點，分別表示為 - 1，0，1，取均值後也是 0。兩者就無法區分了。) 。

GNN 的形狀和過平滑問題

每加一個新層，節點表示中就會包含越來越多的節點資訊。

一個節點，在第一層，只會聚合它的直接鄰節點的資訊。到第二層，它們仍然只聚合直接鄰節點資訊，但這次，他們的直接鄰節點的表示已經包含了它們各自的鄰節點資訊 (從第一層獲得) 。經過 n 層後，所有節點的表示變成了它們距離為 n 的所有鄰節點的聚合。如果全圖的直徑小於 n 的話，就是聚合了全圖的資訊！

如果你的網路層數過多，就有每個節點都聚合了全圖所有節點資訊的風險 (並且所有節點的表示都收斂至相同的值) ，這被稱為過平滑問題 (the oversmoothing problem)。

這可以通過如下方式來解決：

  • 在設計 GNN 的層數時，要首先分析圖的直徑和形狀，層數不能過大，以確保每個節點不聚合全圖的資訊
  • 增加層的複雜性
  • 增加非訊息傳遞層來處理訊息 (如簡單的 MLP 層)
  • 增加跳躍連線 (skip-connections)

過平滑問題是圖機器學習的重要研究領域，因為它阻止了 GNN 的變大，而在其他模態資料上 Transformers 之類的模型已經證明了把模型變大是有很好的效果的。

圖 Transformers

沒有位置嵌入 (positional encoding) 層的 Transformer 模型是置換不變的，再加上 Transformer 模型已被證明擴充套件性很好，因此最近大家開始看如何改造 Transformer 使之適應圖資料 (綜述) 。多數方法聚焦於如何最佳表示圖，如找到最好的特徵、最好的表示位置資訊的方法以及如何改變注意力以適應這一新的資料。

這裡我們收集了一些有意思的工作，截至本文寫作時為止，這些工作在現有的最難的測試基準之一 斯坦福開放圖測試基準 (Open Graph Benchmark, OGB) 上取得了最高水平或接近最高水平的結果：

  • Graph Transformer for Graph-to-Sequence Learning (Cai and Lam, 2020) 介紹了一個圖編碼器，它把節點表示為它本身的嵌入和位置嵌入的級聯，節點間關係表示為它們間的最短路徑，然後用一個關係增強的自注意力機制把兩者結合起來。
  • Rethinking Graph Transformers with Spectral Attention (Kreuzer et al, 2021) 介紹了譜注意力網路 (Spectral Attention Networks, SANs) 。它把節點特徵和學習到的位置編碼 (從拉普拉斯特徵值和特徵向量中計算得到) 結合起來，把這些作為注意力的鍵 (keys) 和查詢 (queries) ，然後把邊特徵作為注意力的值 (values) 。
  • GRPE: Relative Positional Encoding for Graph Transformer (Park et al, 2021) 介紹了圖相對位置編碼 Transformer。它先在圖層面的位置編碼中結合節點資訊，在邊層面的位置編碼中也結合節點資訊，然後在注意力機制中進一步把兩者結合起來。
  • Global Self-Attention as a Replacement for Graph Convolution (Hussain et al, 2021) 介紹了邊增強 Transformer。該架構分別對節點和邊進行嵌入，並通過一個修改過的注意力機制聚合它們。
  • Do Transformers Really Perform Badly for Graph Representation (Ying et al, 2021) 介紹了微軟的 Graphormer, 該模型在面世時贏得了 OGB 第一名。這個架構使用節點特徵作為注意力的查詢 / 鍵 / 值 (Q/K/V) ，然後在注意力機制中把這些表示與中心性，空間和邊編碼資訊通過求和的方式結合起來。

最新的工作是 Pure Transformers are Powerful Graph Learners (Kim et al, 2022)，它引入了 TokenGT。這一方法把輸入圖表示為一個節點和邊嵌入的序列 (並用正交節點標識 (orthonormal node identifiers) 和可訓練的型別標識 (type identifiers) 增強它) ，而不使用位置嵌入，最後把這個序列輸入給 Tranformer 模型。超級簡單，但很聰明！

稍有不同的是，Recipe for a General, Powerful, Scalable Graph Transformer (Rampášek et al, 2022) 引入的不是某個模型，而是一個框架，稱為 GraphGPS。它允許把訊息傳遞網路和線性 (長程的) transformer 模型結合起來輕鬆地建立一個混合網路。這個框架還包含了不少工具，用於計算位置編碼和結構編碼 (節點、圖、邊層面的) 、特徵增強、隨機遊走等等。

在圖資料上使用 transformer 模型還是一個非常初生的領域，但是它看上去很有前途，因為它可以減輕 GNN 的一些限制，如擴充套件到更大 / 更稠密的圖，抑或是增加模型尺寸而不必擔心過平滑問題。

更進階的資源

如果你想鑽研得更深入，可以看看這些課程：

不錯的處理圖資料的庫有
PyGeometric (用於圖機器學習) 以及 NetworkX (用於更通用的圖操作)。

如果你需要質量好的測試基準，你可以試試看：

如果想要更多的資料集，可以看看:

外部影象來源

縮圖中的 Emoji 表情來自於 Openmoji (CC-BY-SA 4.0)，圖元的圖片來自於 Biological network comparison using graphlet degree distribution (Pržulj, 2007)。

英文原文: https://huggingface.co/blog/intro-graphml

譯者: Matrix Yao (姚偉峰)