河北小夥深耕OI被圖論困擾多年 終於研究出最新的存圖方式 速看！指向立體星(隨便起的名）的建立與使用

河北小夥深耕OI被圖論困擾多年 終於研究出最新的存圖方式 速看！

在圖論中，我們經常使用不同種的資料結構來儲存圖的資訊，同時要適應演演算法的需要；
其中較為節省記憶體的包括了鏈式前向星和鄰接表，但是對於最基本的最短路初學者一般用不到，因此，我在此介紹一種基於結構體的儲存方式——「指向立體星」
一 指向立體星的搭建

struct ver
{
  int no;//節點編號
  int dat;//點權
  int tnum;//出度
  int to[N];//通往的點（儲存的數量應該等於tnum）
  int k1[N];//出度的邊權
  int edge1[N];//出度的邊的編號
  int fnum;//入度
  int from[N];//入度邊的起始點
  int k2[N];//入度的邊權
  int edge2[N];//入度的邊的編號
}t[N];

看起來變數很多，實際上我列舉了我能想到的所有可能用到的變數，真正需要計算的不會是全部，看題就好
二 指向立體星的儲存

void add(int x,int y)
{
  t[x].tnum++;
  t[y].fnum++;
  t[x].to[t[x].tnum]=y;
  t[y].from[t[y].fnum]=x;
}

這是最普通的新增點，當然可以精簡一下

void add(int x,int y)
{
	t[x].to[++t[x].tnum]=y;
	t[y].from[++t[y].fnum]=x;
}

如果存其他的東西，（邊的編號，權值等等）函數傳值時傳過來就好啦~
要注意的是這個結構體裡陣列的下標是結構體中的一個資料，呼叫時要看清O-O!
三 實戰應用
拓撲時它是最好用的，其他時候記得結合不同情況找最優的選擇(๑•̀ㅂ•́)و✧

隨機附贈一道例題(NOIP 2003 提高組第一題)
題目背景
人工神經網路（Artificial Neural Network）是一種新興的具有自我學習能力的計算系統，在圖形識別、函數逼近及貸款風險評估等諸多領域有廣泛的應用。對神經網路的研究一直是當今的熱門方向，蘭蘭同學在自學了一本神經網路的入門書籍後，提出了一個簡化模型，他希望你能幫助他用程式檢驗這個神經網路模型的實用性。
題目描述
在蘭蘭的模型中，神經網路就是一張有向圖，圖中的節點稱為神經元，而且兩個神經元之間至多有一條邊相連，下圖是一個神經元的例子：

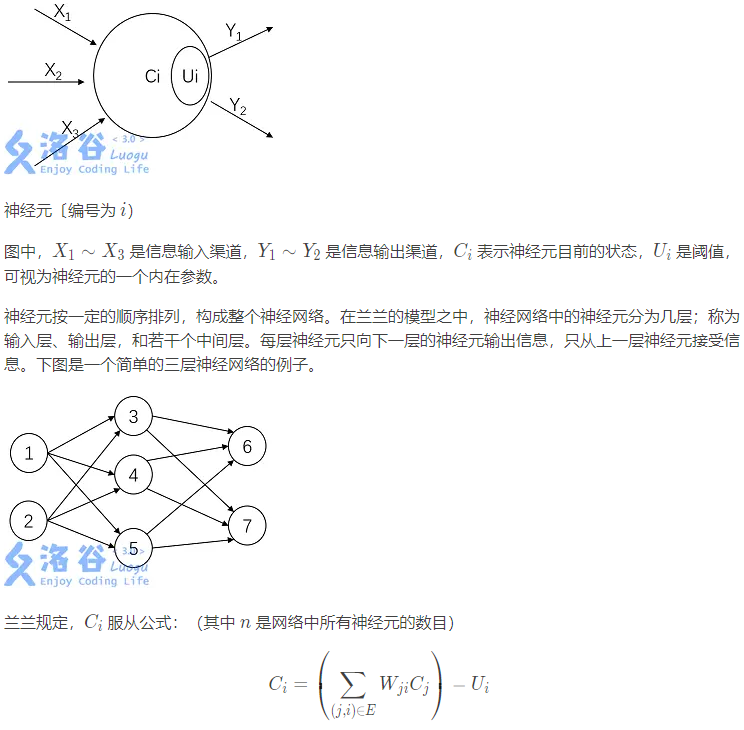
公式中的 Wji（可能為負值）表示連線j號神經元和i號神經元的邊的權值。當C_i大於0時，該神經元處於興奮狀態，否則就處於平靜狀態。當神經元處於興奮狀態時，下一秒它會向其他神經元傳送訊號，訊號的強度為Ci。
如此．在輸入層神經元被激發之後，整個網路系統就在資訊傳輸的推動下進行運作。現在，給定一個神經網路，及當前輸入層神經元的狀態（Ci），要求你的程式運算出最後網路輸出層的狀態。

輸入格式
輸入檔案第一行是兩個整數n（1≤n≤100）和p。接下來n行，每行2個整數，第i+1行是神經元i最初狀態和其閾值(Ui),非輸入層的神經元開始時狀態必然為0。再下面P行，每行由2個整數i,j及1個整數Wij，表示連線神經元i,j的邊權值為Wij
輸出格式
輸出檔案包含若干行，每行有2個整數，分別對應一個神經元的編號，及其最後的狀態2個整數間以空格分隔。僅輸出最後狀態大於0的輸出層神經元狀態，並且按照編號由小到大順序輸出。
若輸出層的神經元最後狀態均為0，則輸出 NULL。

輸入輸出樣例
輸入
5 6
1 0
1 0
0 1
0 1
0 1
1 3 1
1 4 1
1 5 1
2 3 1
2 4 1
2 5 1
輸出
3 1
4 1
5 1

#include<bits/stdc++.h>
using namespace std;
int n,p,quan[120][120];
struct ver
{
	int c,u,ru,chu;
	int ch[90];
	bool ask,isin=1;
}s[120];
int main()
{
	cin>>n>>p;
	for(int i=1;i<=n;i++)
		cin>>s[i].c>>s[i].u;
	int a,b;
	for(int i=1;i<=p;i++){
		cin>>a>>b>>quan[a][b];
		s[b].ru++;
		s[a].ch[++s[a].chu]=b;
		s[b].isin=0; 
	}
	int ans=0;
	while(ans<n)
		for(int i=1;i<=n;i++){
			if((s[i].ru==0&&!s[i].isin&&s[i].c-s[i].u<=0)||(s[i].ru==0&&s[i].c==0&&s[i].isin)){
			 ans++;
			 for(int j=1;j<=s[i].chu;j++)
			 	s[s[i].ch[j]].ru--;
			 continue;
			}
			if(s[i].ru==0&&s[i].ask==0){
				ans++;
				s[i].ask=1;
				if(!s[i].isin)  s[i].c-=s[i].u;
				for(int j=1;j<=s[i].chu;j++)
					s[s[i].ch[j]].ru--,s[s[i].ch[j]].c+=quan[i][s[i].ch[j]]*s[i].c;
			}
		}
	bool ok=0;
	for(int i=1;i<=n;i++)
		if(s[i].c>0&&s[i].chu==0)
		{
			cout<<i<<" "<<s[i].c<<endl;
			ok=1;
		}
		else  continue;
	if(ok==0) cout<<"NULL"<<endl;
	return 0;
}