論文資訊

論文標題：Domain-invariant Feature Exploration for Domain Generalization
論文作者：Wang Lu, Jindong Wang, Haoliang Li, Yiqiang Chen, Xing Xie
論文來源：TMLR 2022
論文地址：download 
論文程式碼：download
參照次數：

1 前言

　　本文將介紹一種基於域不變特徵挖掘的域泛化方法（$\text{DIFEX}$）。近年來，領域泛化(Domain Generalization, DG) 受到了越來越多的關注，現有的 DG 方法可以粗略地分為三類：資料操作、表示學習、學習策略。本文聚焦於域泛化表示學習，針對現有表示學習中獲取的不變特徵不夠充分的問題，嘗試思考：什麼是域不變特徵？如何進一步改進DG的效果？首次將域不變特徵分成域內不變特徵（internally-invariant）和域間不變特徵（mutually-invariant）兩種型別，更多樣、更充分地挖掘域不變特徵。

2 介紹

　　資料操作：對資料輸入輸出進行操作，比如資料增量、資料生成；

　　表示學習：學習域不變特徵或者對特徵進行解耦，獲取更有意義的泛化特徵；

　　學習策略：設計一些特定的策略增強模型泛化能力，比如整合或元學習；

　　本文主要聚焦於表示學習，進行模型泛化能力的增強。已有的關於域不變特徵學習方法的探索促使我們嘗試思考這類方法的合理性：什麼是域不變特徵？如何獲取域不變特徵並更好獲得泛化效果？現有一些工作表明，在域自適應領域，簡單的域間特徵對齊獲取的特徵是遠遠不夠的，需要關注更多其它的方面。最近，在域泛化領域也出現了類似的結論，簡單的對齊可能損害模型的分辨能力以及特徵的多樣性和充分性。針對這個問題，我們對於不變特徵進行了深入的思考。

　　本文認為不變特徵應該從域內和域間兩個角度進行學習：

• • 域內不變特徵（internally-invariant features），與分類有關的特徵，產生於域的內部，不受其他域的影響，主要抓取資料的內在語意資訊；
  • 域間不變特徵（mutually-invariant features），跨域遷移知識，通過多個域產生，共同學習的一些知識；

　　本文認為，把這兩種特徵有效充分地結合起來，可以得到泛化性更好的模型。注意我們的方法類似特徵解耦，但是其實稍有區別，特徵解耦通常將特徵分為域專有特徵和域共有特徵，這裡的域內不變特徵和域專有特徵有稍許區別，更關注於對分類有用的特徵，可以理解為針對分類不變的特徵，而後者強調與域關聯的特徵。廣泛的實驗表明，我們的方法能獲取更多樣、更充分的特徵，從而構建泛化能力更強的機器學習模型。

3 問題定義

　　多源域資料集 $\mathcal{S}=\left\{\mathcal{S}^{i} \mid i=1, \cdots, M\right\}$ ，其中 $\mathcal{S}^{i}=\left\{\left(\mathbf{x}_{j}^{i}, y_{j}^{i}\right)\right\}_{j=1}^{n_{i}}$ 代表著第 $i$ 個源域，每個域的聯合分佈不一樣 $P_{X Y}^{i} \neq   P_{X Y}^{j}, 1 \leq i \neq j \leq M$。域適應的目的是從 $M$ 個訓練的源域學習到一個泛化函數 $h: \mathcal{X} \rightarrow \mathcal{Y}$ 應用到一個不可知的目標域 $\mathcal{S}_{\text {test }}$，使得 $\min _{h} \mathbb{E}_{(\mathbf{x}, y) \in \mathcal{S}_{\text {test }}}[\ell(h(\mathbf{x}), y)]$ 。所有域，包括源域和目標域，都具有相同的輸入空間 $\mathcal{X}^{1}=\cdots=\mathcal{X}^{M}=\mathcal{X}^{T} \in \mathbb{R}^{m}$ 和輸出空間 $\mathcal{Y}^{1}=\cdots=\mathcal{Y}^{M}=\mathcal{Y}^{T}=\{1,2, \cdots, C\}$。

4 動機

　　已有的工作表明傅立葉相值（Phase）中包含更多的語意資訊，不太容易受到域偏移的影響，而傅立葉幅值（Amplitude）資訊主要包含低層次的統計資訊，受域偏移影響較大。從下面的圖中，可以看出，對於行走採集到的原始資料來說，傅立葉的相值資訊的確更能代表類別，僅由相值恢復的資料的確包含更多的語意資訊，比如週期性以及起伏。因此，我們把傅立葉相值作為域內不變特徵。

5 方法

　　整體框架：

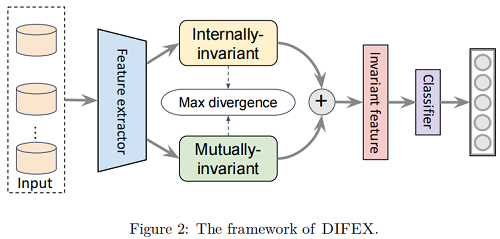
　　如上圖所示，$\text{DIFEX}$ 嘗試同時學習域內不變特徵和域間不變特徵，並嘗試將他們集合起來進行分類。注意，為了保持公平性，我們將最後一層特徵一分為二，一部分進行域內不變特徵學習，一部分進行域間特徵學習；同時為了保證特徵的多樣性，我們提出了一個正則項，來讓兩種特徵的差別儘量大。下面來具體看看兩種特徵的獲取以及多樣性的拓展。

5.1 域不變特徵

　　為了獲取域內不變特徵，主要採用一個簡單的蒸餾框架來學習，注意這裡的蒸餾方法雖然在訓練時候引入了額外的訓練代價，但是在預測時可以減少不必要的FFT計算，確保預測的整個過程可以端到端的直接進行。

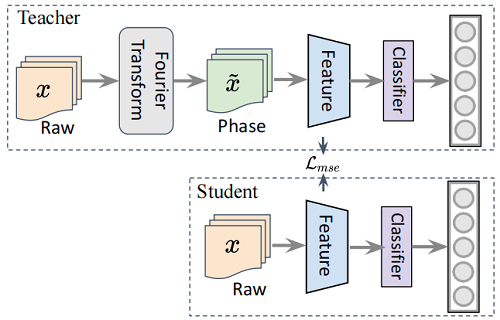
　　如上圖所示，我們首先使用一個老師網路來利用傅立葉相值資訊來學習分類模型，從而獲取有用的與分類有關的傅立葉相值資訊，訓練之後，我們認為老師模型可以得到與分類有關的傅立葉相值資訊，那麼在學生模型訓練的時候，便可以讓它參考老師的這部分特徵，進行域內不變特徵學習。

　　　　$\underset{\theta_{S}^{f}, \theta_{S}^{c}}{\text{min }}      \mathbb{E}_{(\mathbf{x}, y) \sim P \operatorname{tr}} \ell_{c}\left(G_{S}^{c}\left(G_{S}^{f}(\mathbf{x})\right), y\right)+\lambda_{1} \mathcal{L}_{m s e}\left(G_{S}^{f}(\mathbf{x}), G_{T}^{f}(\tilde{\mathbf{x}})\right) \quad\quad\quad(4)$

補充：

　　對單通道二維資料 $x$ 的傅立葉變換 $\mathcal{F}(\mathbf{x})$ 表示為：

　　　　$\mathcal{F}(\mathbf{x})(u, v)=\sum\limits _{h=1}^{H-1} \sum\limits_{w=0}^{W-1} \mathbf{x}(h, w) e^{-j 2 \pi\left(\frac{h}{H} u+\frac{w}{W} v\right)}\quad\quad\quad(1)$

　　其中 $u$ 和 $v$ 是指數。$H$ 和 $W$ 分別是高度和寬度。傅立葉變換可以用 FFT 演演算法有效地計算出來。相位分量隨後表示為：

　　　　$\mathcal{P}(x)(u, v)=\arctan \left[\frac{I(x)(u, v)}{R(x)(u, v)}\right]\quad\quad\quad(2)$

　　其中，$R(x)$ 和 $I(x)$ 分別表示 $\mathcal{F}(\mathbf{x})$ 的實部和虛部。對於具有多個通道的資料，分別計算每個通道的傅立葉變換，得到相應的相位資訊。我們將 $x$ 的傅立葉相位表示為 $\tilde{\mathbf{x}}$，然後，使用 $(\tilde{\mathbf{x}}, y)$ 訓練教師網路：

　　　　$\underset{\theta_{T}^{f}, \theta_{T}^{c}}{\text{min}}  \quad \mathbb{E}_{(\mathbf{x}, y) \sim P^{t r}} \mathcal{L}_{c l s}\left(G_{T}^{c}\left(G_{T}^{f}(\tilde{\mathbf{x}})\right), y\right)\quad\quad\quad(3)$

　　一旦獲得了教師網路 $G_{T}$，我們就使用特徵知識蒸餾來指導學生網路學習傅立葉資訊。這種蒸餾方法的配方如下： 

　　　　$\underset{\theta_{S}^{f}, \theta_{S}^{c}}{\text{min }}      \mathbb{E}_{(\mathbf{x}, y) \sim P \operatorname{tr}} \ell_{c}\left(G_{S}^{c}\left(G_{S}^{f}(\mathbf{x})\right), y\right)+\lambda_{1} \mathcal{L}_{m s e}\left(G_{S}^{f}(\mathbf{x}), G_{T}^{f}(\tilde{\mathbf{x}})\right) \quad\quad\quad(4)$

　　其中，$\theta_{S}^{f}$ 和 $\theta_{S}^{c}$ 是學生網路的特徵提取器 $G_{S}^{f}$ 和分類層 $G_{S}^{c}$ 的可學習引數。$\lambda_{1}$ 是一個權衡超引數，$\mathcal{L}_{m s e}$ 是 $\text{MSE}$ 損失，它可以使學生網路的特徵接近教師網路的特徵。

5.2 互不變特徵

　　如前所述，僅憑傅立葉相位特徵並不足以獲得足夠的鑑別特徵來進行分類。因此，我們通過利用多個訓練領域中包含的跨領域知識來探索互不變的特徵。具體來說，給定兩個域 $\mathcal{S}^{i}$，$\mathcal{S}^{i}$，我們使用相關性對齊方法對它們的二階統計量（相關性）進行對齊：

　　　　$\mathcal{L}_{\text {align }}=\frac{2}{N \times(N-1)} \sum\limits_{i \neq j}^{N}\left\|\mathbf{C}^{i}-\mathbf{C}^{j}\right\|_{F}^{2}\quad\quad\quad(5)$

　　其中，$\mathbf{C}^{i}=\frac{1}{n_{i}-1}\left(\mathbf{X}^{i} \mathbf{X}^{i}-\frac{1}{n_{i}}\left(\mathbf{1}^{T} \mathbf{X}^{i}\right)^{T}\left(\mathbf{1}^{T} \mathbf{X}^{i}\right)\right)$ 是協方差矩陣，$\|\cdot\|_{F}$ 代表著 $F$ 範數。

　　由於域內不變特徵和域間不變特徵之間可能存在重複和冗餘，我們期望兩部分可以儘可能多地提取出不同的不變特徵。這使得特徵有更多的多樣性，有利於泛化。為了實現這個目標，我們通過最大化內部不變（$z_1$）和互不變（ $z_1$）特徵之間的距離，我們稱之為  $\text{exploration loss}$：

　　其中 $d(\cdot, \cdot)$ 是一個距離函數，為了簡單，我們簡單地使用 $L2$ 距離： $ \mathcal{L}_{e x p}=-\left\|\mathbf{z}_{1}-\mathbf{z}_{2}\right\|_{2}^{2} $。

6 DIFEX 總結 

　　綜上所述，我們的方法被分為兩個步驟。首先，我們優化了 $\text{Eq.1}$。其次，優化了以下目標：

　　　　$\underset{\theta_{f}, \theta_{c}}{\text{min}} \;\mathbb{E}_{(\mathbf{x}, y) \sim P^{t r}} \mathcal{L}_{c l s}\left(G_{c}\left(G_{f}(\mathbf{x})\right), y\right)+\lambda_{1} \mathcal{L}_{m s e}\left(\mathbf{z}_{1}, G_{T}^{f}(\tilde{\mathbf{x}})\right)+\lambda_{2} \mathcal{L}_{\text {align }}+\lambda_{3} \mathcal{L}_{\text {exp }}\left(\mathbf{z}_{1}, \mathbf{z}_{2}\right)$