Python物件導向(上)
Python物件導向(上)
python是一門物件導向的程式語言。何為物件?物件是類的範例。在生活中,任何一個事物都是一個物件,如牡丹花。牡丹花的類是花類,同樣屬於花類的還有荷花、月季花、金銀花、菊花、梅花、蘭花等,它們都是花科,但是每一朵花都有不同的枝葉,不同的色彩,不同的長相。這就是花類的各個屬性了,如玫瑰花是紅色,菊花是黃色……除了屬性,物件裡還有方法,也就是花兒怎樣開花,怎樣長出形態等。
我們來剖析一下分數的構成,一個分數由 分子、分母構成,分子在上,分母在下。分子可以取任意整數,分母的值不能等於0。
現在我們就可以建立一個分數類:
class Fraction:
def __init__ (self, top, bottom):
self.num = top
self.den = bottom
所有的類都應該寫構造方法,在python中,構造方法一般是__init__。Self是一個總是指向物件本身的特殊引數,它必須是第一個形式引數。然而,在呼叫方法時,從來不需要提供相應的實際引數。
在建構函式中,self.num與self.den定義了分子與分母,也就是說,呼叫物件時傳入的初始值給其二者賦予:
Myfra = Fraction(3, 5)
#建立了一個物件Myfra,並給予初始值3和5,對應分子分母,所以為三分之五
如果我們要將此物件的值(也就是三分之五)列印出來,我們則需要定義一個show()方法:
def show(self):
print(str(self.num)+「/」+ str(self.den))
然後我們呼叫這個方法:
Myfra.show()
這樣就可以顯示出它的值了。但其實我們有更好的實現:
def __str__(self):
return str(self.num) +「/ 」+str( self.den))
因為python中有一套標準方法,我們可以重寫它們,也就是重新定義他們,來使我們的程式更加簡便。如此呼叫過程則為:
Myfra = Fraction(3, 5)
print(Myfra)
我們可以根據這種方式來重新其他的標準方法,如實現分數之間的加法運算:
def __add__ (self, otherFraction):
newNum = self.num * otherFraction.den + \
self.den * otherFraction.num
newDen = self.den * otherFraction.den
return Fraction(newNum, newDen)
如果要使得兩個分數相加,最簡單的方法就是:
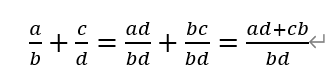
由上式可得上述程式,接著呼叫:
F1 = Fraction(1,4)
F2 = Fraction(1,2)
F3 = F1 + F2
print(F3)
上述程式雖然可以相加,但不是最簡分數,我們可以運用歐幾里得演演算法尋得最大公因數(GCD),然後將分子分母分別除以最大公因數,結果就是最簡分數。
歐幾里得演演算法中,對於整數m和n,如果m能被n整除,那麼它們的最大公因數就是n。如果m不能被n整除,那麼結果是n與m除以n的餘數的最大公因數。
def gcd(m, n):
while m % n != 0:
oldm = m
oldn = n
m = oldn
n = oldm%oldn
return n
我們通過上述程式可以迭代出最大公因數,但是需要注意的是,此程式的分數不能為負數。
#改良版分數的加法
def __add__(self, otherFraction):
newNum = self.num * otherFraction.den + \
self.den * otherFraction.num
newDen = self.den * otherFraction.den
common = gcd(newNum, newDen)
return Fraction(newNum // common, newDen // common)
為了讓兩個分數進行比較,還需要怎加一個方法,我們可以通過重寫內建方法__eq__來實現。
def __eq__(self, other):
firstNum = self.num * other.den
secNum = other.num * self.den
return firstNum == secNum
如果我們沒有重寫__eq__方法,那麼預設比較的是兩個物件範例,如果是指向同一個範例的物件,那麼他們兩個才能相等,這被稱為淺相等。而我們重寫後,兩個物件只有值相同時,才是相等的,這被稱為深相等。
所有程式碼如下:
class Fraction:
def __init__(self, top, botton):
self.num = top
self.den = botton
def __str__(self):
return str(self.num) + "/" + str(self.den)
def __add__(self, otherFraction):
newnum = self.num * otherFraction.den + self.den * otherFraction.num
newden = self.den * otherFraction.den
common = gcd(newnum, newden)
return Fraction(newnum // common, newden // common)
def __eq__(self, otherFraction):
firstnum = self.num * otherFraction.den
secnum = self.den * otherFraction.num
return firstnum == secnum
def gcd(m, n):
while m % n != 0:
oldm = m
oldn = n
m = oldn
n = oldm % oldn
return n
if __name__ == '__main__':
f1 = Fraction(3, 4)
f2 = Fraction(3, 4)
f3 = f1 + f2
print(f3)
print(f1 == f2)
f4 = Fraction(4, 8)
f5 = Fraction(2, 4)
print(f4 == f5)
print(f4 + f5)