計算機中數值和字串怎麼用二進位制表示?
作者:小牛呼嚕嚕 | https://xiaoniuhululu.com
計算機內功、JAVA底層、面試、職業成長相關資料等更多精彩文章在公眾號「小牛呼嚕嚕」
大家好,我是呼嚕嚕。我們都知道現代計算機採用 0 和 1 組成的二進位制,來表示所有的資訊。那大家是不是有時候會有這些疑問:為什麼計算機採用了二進位制?二進位制是如何表示計算機的相關資訊的?比如數位、字串、聲音、圖片、視訊等等
進位制
進位計演演算法是一種常見的計算方式,常見的有十進位制,二進位制,十六進位制
- 十進位制
十進位制,都是以0-9這九個數位組成,不能以0開頭, 逢十進一。
十進位制是我們從小就潛移默化般學習的,我們大多數人擁有的手指或腳趾的數目就是10,天生讓我們適合十進位制為基礎的數位系統
- 二進位制
二進位制,數位中只有 0 和 1,逢二進一
- 八進位制
八進位制,數位0-7,逢八進一
- 十六進位制
十六進位制,數位有 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F組成,逢十六進一。
其表示形式比較特殊,因為10~15不能用數位來展示,所以強制規定:10 用 A 表示、11 用 B 表示、12 用 C 表示、13 用 D 表示、14 用 E 表示、15用F表示
進位制間的轉換
- R進位制 → 十進位制:按權展開
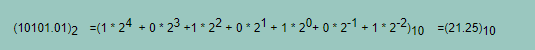
- 十進位制 → R進位制:整數小數分開處理
- 整數部分的轉換方法是:「除基取餘,上右下左」。即用要轉換的十進位制整數去除以基數R,將得到的餘數作為結果資料中各位的數位,直到餘數為0為止。上面的餘數(先得到的餘數) 作為右邊低位上的數位,下面的餘數作為左邊高位上的數位。
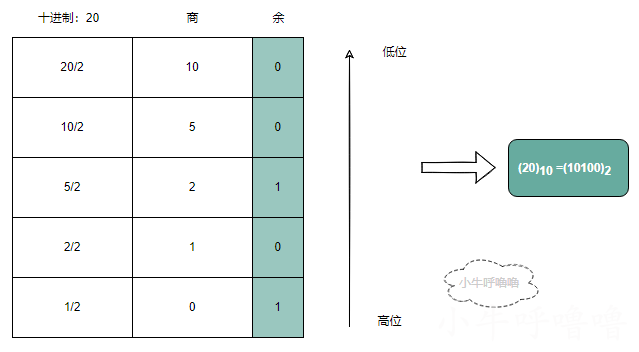
- 小數部分的轉換方法是:「乘基取整,上左下右」。即用要轉換的十進位制小數去乘以基數R,將得到的乘積的整數部分作為結果資料中各位的數位,小數部分繼續與基數R相乘。以此類推,直到某步乘積的小數部分為0或已得到希望的位數為止。最後,將上面的整數部分作為左邊高位上的數位,下面的整數部分作為右邊低位上的數位。
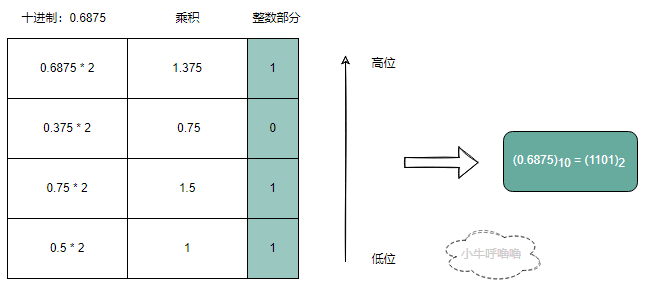
我們需要注意的是:在轉換過程中,可能乘積的小數部分總得不到0,即轉換得到希望的位數後還有餘數,這種情況下得到的是近似值。
- 二進位制轉八進位制、十六進位制
由於把二進位制的三位看成一個整體就是八進位制的數,二進位制的四位也就是十六進位制的數。通過這個規律,我們很容易地就能實現二進位制與八進位制、十六進位制的相互轉換。
整數部分從低向高每3或4位元數用一個等值八/十六進位制數替換,不足時高位補0;小數部分從高向低每3或4位元數用一個等值八或十六進位制數替換,不足時低位補0

- 八進位制、十六進位制 轉二進位制
每一位數改成等值的3或4位元二進位制數,整數部分高位0省略;小數部分低位0省略

計算機為什麼使用二進位制?
我們從小更熟悉十進位制的運算,0、1、2、3、4、5、6、7、8、9十個數位,逢十進一。但是計算機中使用二進位制,只有0和1兩個數位,逢二進一。
採用二進位制的原因:
- 二進位制在自然界中最容易被表現出來。自然界中二值系統非常多,電壓的高低、水位的高低、門的開關、電流的有無等等都可以組成二值系統。
- 計算機使用二進位制和現代計算機系統的硬體實現有關。製造二個穩定態的物理器件容易,使得組成計算機系統的邏輯電路通常只有兩個狀態,即開關的接通與斷開。由於每位資料只有斷開與接通兩種狀態,因此二進位制的資料表達具有抗干擾能力強、可靠性高的優點
- 二進位制非常適合邏輯運算,可方便地用邏輯電路實現 算術運算
機器數和真值
機器數
一個數在計算機中的二進位制表示形式, 叫做這個數的機器數、機器碼。
由於我們平時不僅使用的是正數,還有大量的負數,而計算機是無法識別符號"+","-", 所以計算機規定,用二進位制數的最高位0表示正數,如果是1則表示負數。機器數是帶符號的
如果十進位制中的數 +3 ,計算機字長為8位元,轉換成二進位制的機器數就是0000 0011。如果是-3,就是 10000011
真值
帶符號位的機器數對應的真正數值是 機器數的真值,我們知道機器數的第一位是符號位, 比如1000 0011直接轉換成十進位制為131,但實際上最高位1 是負號,其真正的值為 [-3]
機器數的編碼形式有哪些?
原碼
原碼就是符號位加上真值的絕對值, 即用最高位表示符號, 其餘位表示值
比如如果是8位元二進位制:
- [+1] = (0000 0001)原
- [ -1] = (1000 0001)原
我們人類根據二進位制的規則,可以一眼就明白原碼代表的數位,方便了人類
面試的時候有一個經典的問題:8位元二進位制數原碼的取值範圍是?
我們只需將除了最高位,用來表示符號,其他位都是1,即[1111 1111 , 0111 1111],換算成十進位制:[-127 , 127]
那n位二進位制數呢?

取值範圍:

現在看起來都是那麼美好,然而當我們將正負數相加時,遇到了問題:2個[+1]相減 ,其實就相當於[+1] 和 [-1] 相加,我們的預期是0,
但計算機實際上計算時:(0000 0001)原+(1000 0001)原=(1000 0010)原 =[-2]

為了解決這個問題,反碼就應運而生了
反碼
反碼主要是針對負數的,正數的反碼是其本身,負數的反碼是在其原碼的基礎上, 符號位不變,其餘各個位取反
- [+1] = (0000 0001)原 = (0000 0001)反
- [-1] = (10000001)原 = (1111 1110)反
反碼如果是表示的一個正數,那我們還是一眼就能知道他的數值,但如果是負數的反碼時,我們就需要轉換成原碼才能看出它的真值。
如果最高位有進位出現,則要把它送回到最低位去相加(迴圈進位)的
[- 1] = (1000 0001)原 = (1111 1110)反
[+7] = (0000 0111)原 =(0000 0111)反
[-1] + [+7] = (1111 1110)反 +(0000 0111)反= (1 0000 0101)反 = (0000 0110)反 =[+ 6]
2個正數相減:[+1] - [+1] = [+1] + [-1] = (0000 0001)反 + (1111 1110)反 = (1111 1111)反 =(1000 0000)原 = [**-0**]
這樣就完美實現了「正負相加等於0",但奇怪的是 ,這個[-0]是有符號的,這就要歸因於 原碼的設計之初,存在的問題,
- (1000 0000)原=[- 0]
- (0000 0000)原=[+0]
對的,你沒看錯,零竟然有2個,習慣計算機的萬事萬物一一對應,嚴謹認真的工程師們表示無法接受,得想辦法去掉[-0],最後他們就發現了神奇的二補數

二補數
二補數的規則:針對負數繼續改進了思路:正數的二補數就是其本身。負數的二補數是在其原碼的基礎上, 符號位不變, 其餘各位取反, 最後一位+1。即在反碼的基礎上最後一位+1
[+1] = (0000 0001)原 = (0000 0001)反 = (0000 0001)補
[-1] = (1000 0001)原 = (1111 1110)反 = (1111 1111)補
[+1] - [+1] = [+1] + [-1] = (0000 0001)補 + (1111 1111)補 = (1 0000 0000)補 = (0000 0000)補 = [0]
如果二補數在補一位1的時候,發生最高位進位,會自動丟掉最高位。期間參照了計算機對符號位的自動處理,利用了最高位進位的自動丟棄實現了符號的自然處理。
那(1000 0000)補 那現在表示多少?-128
- (1000 0000)補 =-1 * 2^7 =[-128]
- (1011)補 = -1 * 2^3 + 02^2 + 12^1 + 1*2^0 = -5
- (0011)補 = 0 * 2^3 + 02^2 + 12^1 + 1*2^0 =3
如果是8位元二進位制, 使用原碼或反碼錶示的範圍為[-127, +127], 而使用二補數表示的範圍為[-128, 127],使用二補數還能夠多表示一個最低數
二補數其實脫胎於 模運算系統:
比如一天中的24小時是一個模運算系統,任意時刻的鐘點數都是0到23間的一個整數,這有點類似24進位制
- 今天的第24點,就是明天的0點;
- 今天的25點,就是明天的凌晨1點;
- 今天的-4點,就是昨天的20點,我們稱20是-4對模24的二補數,模就是容量、極值的意思
再舉個例子:鐘錶上的12個刻度也是一個模運算系統。假定時鐘現在指向10,要把指標只向6,有兩種方法
- 倒撥4格:10 - 4 = 6
- 正撥8格:10 + 8 = 18 = 6 (mod 12)
所以模12系統中 -4 = 8 (mod 12),我們稱8是-4對模12的二補數
一個模運算系統中:一個負數可以用它的正補數(負數的二補數)代替,一個負數的二補數 = 模 - 該負數的絕對值
那我們之前公式 一個負數的二補數 = 符號位不變, 其餘各位取反, 最後一位+1,是怎麼來的?
負數的原碼 取反 再加1, 這只是方便大家記憶的手段,實際上它相當於加一個模256也就是2^8,為什麼要拆,這是由於8位元機,8位元2進位制數,至能表示0~255個數,一共256個數,所以它是表示不了256這個值的,只能是255+1。由於計算機系統裡面不僅只有正數,還有負數呢,這個該怎麼表示?
計算機大師就想到了,可以將256個數一分為二,規定最高位為符號位,最高位1開頭的表示為負數,最高位0開頭表示正數。我們這裡需要注意一下,特殊的0,所以8位元2進位制數表示範圍就變成了[-128,127],這個範圍是不是很熟悉!
[-1] = (1000 0001)原 = (1111 1110)反 = (1111 1111)補,如果符號位參與計算,(1111 1111)補 的十進位制 等於 255。而255 + |-1|= 256,也就是模。二補數本天成,妙手偶得之

小結一下:
- 二補數不僅解決了[-0]的問題,更核心的是讓計算機做減法運算,變成加法運算。
A - B = A + B的二補數 - 使用二補數,將減法變成加法運算,這樣硬體上只需有加法器即可,不需要其他硬體,降低了電路的複雜度
- 使用二補數,不浪費編碼個數,儲存空間利用率高
- 二補數可以用n&0判斷負數奇偶
- 所以計算機底層儲存資料時使用的是二進位制數位,但是計算機在儲存一個數位時並不是直接儲存該數位對應的二進位制數位,而是儲存該數位對應二進位制數位的二補數

定點數和浮點數
定點數
定點數的意思是:即約定機器中所有資料的小數點位置是固定不變的。通常將定點資料表示成純小數或純整數,為了將數表示成純小數,通常把小數點固定在數值部分的最高位之前;而為了將數表示成純整數,則把小數點固定在數值部分的最後面。
例如:十進位制的 25.125
- 整數部分:25使用二進位制表示為:11001
- 小數部分:0.125使用二進位制表示為:.001
- 所以合起來使用11001.001 表示十進位制的25.125
本文的原碼、反碼、二補數概念都是基於定點數
浮點數
定點數表示法的缺點在於其形式過於僵硬,固定的小數點位置決定了固定位數的整數部分和小數部分,不利於同時表達特別大或特別小的數,最終,絕大多數現代的計算機系統採納了浮點數表達方式,這種表達方式利用科學計數法來表達實數,即用一個尾數(Mantissa,尾數有時也稱為有效數位,它實際上是有效數位的非正式說法),一個基數(Base),一個指數(Exponent)以及一個表示正負的符號來表達實數
例如:
- 352.47 = 3.5247 * 10的2次方
- 178.125轉化為二進位制為 10110010.001,又可表示為:1.0110010001 乘以 2的111次方(111是7的二進位制表示)
- 123.45用十進位制科學計數法可以表示為1.2345x10的2次方,其中1.2345為尾數,10為基數,2為指數。浮點數利用指數達到了浮動小數點的效果,從而可以靈活地表達更大範圍的實數。
字串編碼
ASCII 碼
在計算機中, 不僅數值可以用二進位制表示,字串也能用二進位制表示。上世紀美國製定了一套字元編碼,對英語字元與二進位制位之間的關係,加上數位和一些特殊符號, 然後用 8 位的二進位制,就能表示我們日常需要的所有字元了,這個就是我們常常說的ASCII 碼
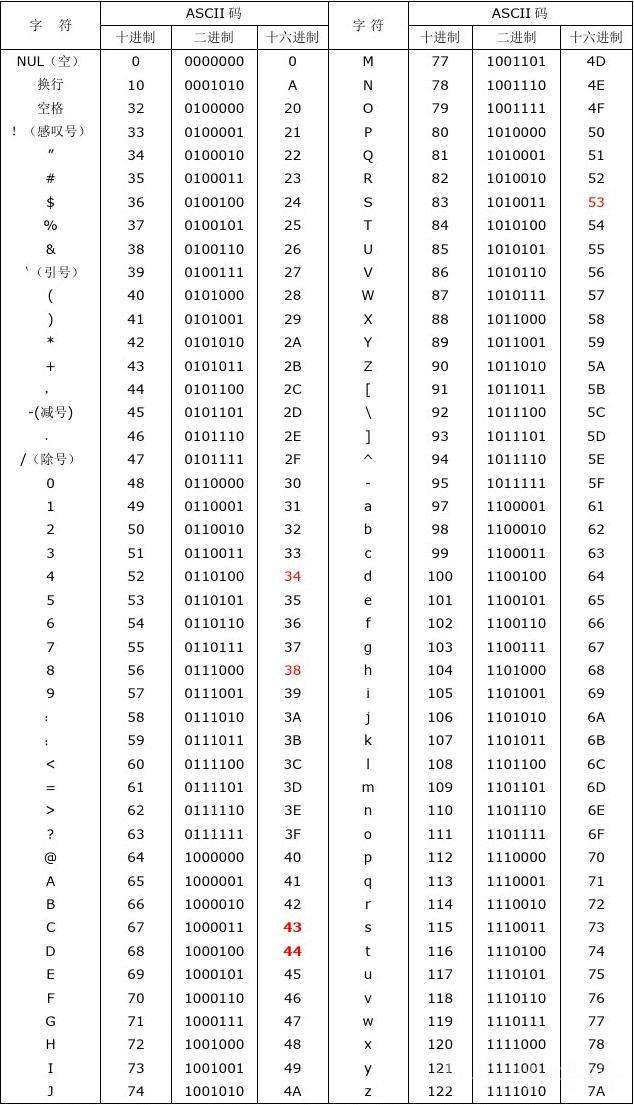
ASCII 碼就好比一個字典,將二進位制和字元一一對應。其中我們看幾個典型的例子:
小寫字母 a在 ASCII 裡面,十進位制97,也就是二進位制的0 110 0001,而大寫字母 A,十進位制65,對應的二進位制 0 100 0001- 需要注意的是,裡面的數位,比如
數位1,二進位制對應0000 0001在ASCII 裡面,表示的其實是字元"1",對應的二進位制是0 011 0001 - 字串 15 也不是用
0000 1111這 8 位二進位制來表示,而是變成兩個字元 1 和 5 連續放在一起,也就是0 011 0001和0 011 0101,需要用兩個 8 位二進位制來表示 。所以**計算機儲存資料時,二進位制序列化會比直接儲存文字能節省大量空間 **
EASCII:擴充套件的 ASCII
一開始美國編寫ASCII表,英語用128個符號編碼就夠了,但隨著計算機的普及,西歐國家不全是英語國家,有德語,法語等等
比如 字母上方有注音符號,它就無法用 ASCII 碼錶示。於是歐洲工程師就決定,利用位元組中閒置的最高位編入新的符號。他們把 ASCII 擴充變成了 EASCII,這擴充的包括希臘字母、特殊的拉丁符號等。由於 ASCII 只佔了 7 位,所以 EASCII 把第 8 位利用起來,仍然是一個位元組來表示,這時表示的字元個數是 256。
Unicode
但 EASCII 並沒有成功,西歐國家以及各個 PC 廠商各自定義出了好多不同的編碼字元集,ISO-8859將西歐國家的編碼一起包含進去。
但隨著計算機來到中國,那些歐美國家把 現有的字典都用完,而且漢字有十多萬個,所以急需新的"字典"。GB2312編碼就出來了,使用兩個位元組表示一個漢字(漢字太多),所以理論上最多可以表示 256 x 256 = 65536 個符號。後來GBK編碼 將古漢字等生僻字加進來。臺灣地區又創造了BIG5編碼,再後來GB18030對東南亞地區的文字,進行了統一。簡單瞭解下這些編碼,就不具體展開了
再後來計算機全球普及,各個國家地區的文字編碼太多太亂,Unicode編碼的出現,為了統一全世界的所有字元。Unicode 是一個很大的集合,現在的規模可以容納100多萬個符號。
由於Unicode 只是一個字元集(Charset),它只規定了符號的二進位制程式碼,卻沒有規定這個二進位制程式碼應該如何儲存,也就是字元編碼(Character Encoding),這就導致計算機無法區別 Unicode 和 ASCII ,比如三個位元組表示一個符號,而不是分別表示三個符號呢?
隨著網際網路的崛起,UTF-8 就是在網際網路上使用最廣的一種 Unicode 的實現方式。UTF-8 它是一種變長的編碼方式。它可以使用1~4個位元組表示一個符號,根據不同的符號而變化位元組長度。Unicode 字元集中的大部分漢字,如果用 UTF-8 編碼的話,是佔 3 個位元組的。
下面我們看看UTF-8是如何相容Unicode的:
UTF-8編碼致力於統一世界上所有的字元集,所以它的設計上既向下相容ASCII碼的編碼方式,同時又考慮了可拓展性,規則如下:
1)對於單位元組的符號:位元組的第一位設為0,後面7位為這個符號的 Unicode 碼。與 ASCII 編碼規則相同;
2)對於n位元組的符號(n > 1):第一個位元組的前n位都設為1,第n + 1位設為0,後面位元組的前兩位一律設為10。剩下的沒有提及的二進位制位,全部為這個符號的 Unicode 碼。
| Unicode | UTF-8 | byte 數 |
|---|---|---|
| 0000~007F | 0XXX XXXX | 1 |
| 0080~07FF | 110X XXXX 10XX XXXX | 2 |
| 0800~FFFF | 1110 XXXX 10XX XXXX 10XX XXXX | 3 |
| 1 0000~1F FFFF | 1111 0XXX 10XX XXXX 10XX XXXX 10XX XXXX | 4 |
我們可以發現,UTF-8 編碼的第一位如果是 0,則只有一個位元組,跟 ASCII 編碼完全一樣,所以相容了。如果是 110 開頭,則是兩個位元組,以此類推如上表所示。所以開頭幾位的值,是編碼本身,同時又是判斷後續還有幾個位元組數的推碼(通過推碼才能判斷這個位元組之後還有幾個位元組共同參與一個字元的表示)
亂碼的來源
編碼是把資料從一種形式轉換為另外一種形式的過程,而解碼則是編碼的逆向過程。編碼是一種格式,解碼是另一種格式,當然會出問題。下面我們舉個例子,來看看這個問題:
- 建立hello.txt檔案,用
Notepad++開啟編輯,以UTF-8格式寫入你好 - 然後我們改變
Notepad++的formaat格式,改為GB2312,然後你好就變成了浣犲ソ
在UTF-8 字典中,你好兩個字的16進位制編碼分別是E4BDA0、E5A5BD
在GB2312字典中,浣犲ソ三個字的16進位制編碼分別是 E4BD、A0E5、A5BD
由於在UTF-8 編碼漢字是 3 個位元組,在GB2312編碼漢字卻是2個位元組,計算機用GB2312去解析UTF-8,硬生生的把3個位元組以每2個位元組為一組去解碼,所以才會有出現這種亂碼。當我們知道亂碼出現的原因,如何解決就變的非常簡單了

參考資料:
《編碼:隱匿在計算機軟硬體背後的語言》
《深入理解計算機系統 第三版》
《計算機組成原理》
《深入計算機組成原理》
https://www.ruanyifeng.com/blog/2007/10/ascii_unicode_and_utf-8.html
https://www.zhihu.com/question/20159860
https://blog.csdn.net/f919976711/article/details/116714860
本篇文章到這裡就結束啦,很感謝靚仔你能看到最後,如果覺得文章對你有幫助,別忘記關注我!
計算機內功、JAVA原始碼、職業成長、專案實戰、面試相關資料等更多精彩文章在公眾號「小牛呼嚕嚕」
