說起加密演演算法，大的分類上，常規區分通常會區分為對稱加密與非對稱加密兩種，兩種演演算法都各有優缺點。然而網際網路發展到今天，應用更廣的還是非對稱加密的方式，而非對稱加密中，RSA又首當其中，被廣泛運用到各類應用中。本人作為一個標準的Javer，一直對RSA細節沒有深入探究，本文算是對該演演算法的一個淺析，其中涉及大量的資料公式推導，當遇到大家耳熟能詳的資料公式（例如費馬定理）時，便不再展開

一、對稱加密

關於對稱加密，網路的釋義很多，有的博主將其定義為「加密和解密使用同一個祕鑰就是對稱加密」。這樣的定義一般值得都是演演算法透明，金鑰不透明的場景，例如加解密雙方使用的都是DES演演算法，在密文傳遞的同時，金鑰也需要傳遞過去

其實所謂對稱加密，即解密是加密的逆運算；比如將一個寶物裝進箱子中，然後將其鎖上，經過一段路途的運輸，收件人收貨後，將鎖開啟，然後將寶物搬出來，流程是這樣進行的：

寶物 --> 放入箱子 --> 上鎖 -----運輸至目的地------ 解鎖 --> 箱子中取出 --> 寶物

可見解密是加密的逆運算，我們便可稱之為對稱加密。應用到程式中，假如我們現在有這樣一段文字：

Attack tomorrow morning

我們將每個字元對應的ASCII都統一加一，對應的密文即變為

@Test
public void encrypt() {
    String str = "Attack tomorrow morning";
    char[] chars = str.toCharArray();
    for (int i = 0; i < chars.length; i++) {
        chars[i] = (char) (chars[i] + 1);
    }
    System.out.println(new String(chars));  // 結果為 "Buubdl!upnpsspx!npsojoh"
}

Buubdl!upnpsspx!npsojoh

而將其解密的原理也就顯而易見，將值統一減一

@Test
public void decrypt() {
    String str = "Buubdl!upnpsspx!npsojoh";
    char[] chars = str.toCharArray();
    for (int i = 0; i < chars.length; i++) {
        chars[i] = (char) (chars[i] - 1);
    }
    System.out.println(new String(chars));  // 結果為 "Attack tomorrow morning"
}

其實在演演算法公開的背景下，此處「1」便是金鑰，傳送方將密文傳送的同時，需要將「1」也傳送出去，這樣接收方便可通過這個「1」對密文進行解密

優點	缺點
演演算法公開、計算量小、加密速度快、加密效率高	祕鑰的管理和分發非常困難，不夠安全。上文中，我們的金鑰其實就是「1」，但在實際應用的場景中，我們需要將金鑰同步給使用方，並且每個使用者的金鑰都需要保證唯一，且一方的金鑰一旦洩露，那麼資料肯定也就不安全了，而隨著使用者的增多，這會使得收、發雙方所擁有的鑰匙數量巨大，金鑰管理成為雙方的負擔

常見的有對稱加密演演算法有DES、AES、3DES等

二、非對稱加密-RSA

非對稱加密是相對「對稱加密」而言的，拿上文從箱子中取出寶物的例子來說，解密流程可能是將箱子的側面開啟，將寶物取出，亦或是直接將箱子砸碎，反正一定不是加密的逆流程

2.1、加密形式

RSA的金鑰有2個

• Public Key 即公鑰，對外公佈的，所有人都可以直接查詢到
• Private Key 即私鑰，只有金鑰的提供者擁有，用來將密文解析出明文的關鍵key

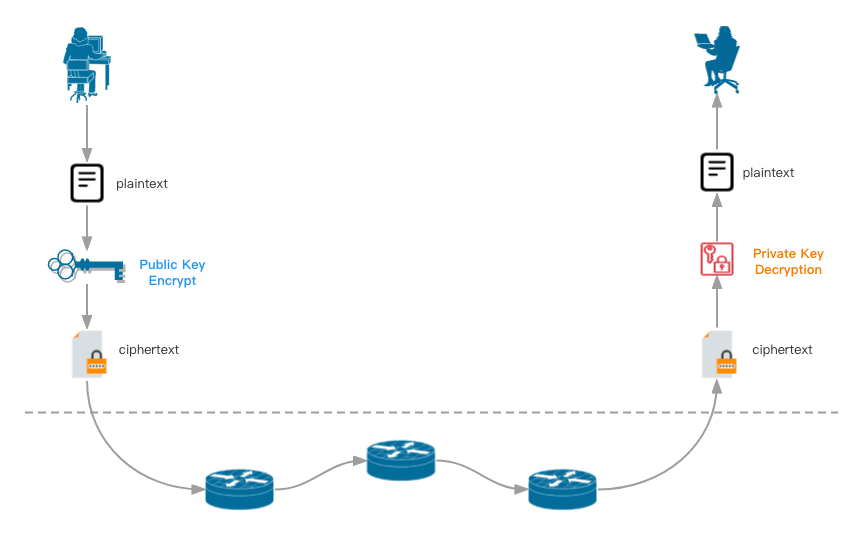
一般是服務的提供者將Public Key公佈給所有人，或者索性掛在自己的網站上（證書檔案），需要連線該服務的使用者端，下載證書並與之建立聯絡。有同學可能會有疑問，Public Key一樣的話，資訊如果被其他人截獲，豈不造成資料洩露？ 其實這個擔心是多餘的，因為只有擁有了私鑰才能解密密文，而私鑰是隻有服務提供者才會擁有的獨一份資料

2.2、加密概述

RSA生成公鑰、私鑰的流程是這樣的

引數	說明
p	大質數
q	大質數
n	n = p * q
z	z = φ(n) = (p-1) * (q-1) 尤拉函數
e	要求(e < n)，且與 z 互質
x	要求 (e * x) % z == 1

此時，公鑰、私鑰也就生成了

• 公鑰 (n, e)
• 私鑰 (n, x)

加密操作（m為明文，c為密文）：

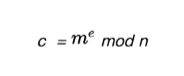
解密操作（m為明文，c為密文）：

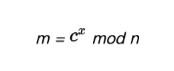
舉例說明，為了方便計算，我們取較小的n：

引數	計算過程	最終取值
p	-	3
q	-	5
n	n = p * q	15
z	z=φ(n)=(p-1)*(q-1)=2*4=8	8
e	e<n且與z互質，隨便取一個小的	7
x	要求 (e * x) % z == 1	15

因此

公鑰為：(15, 7)

私鑰為：(15, 15)

根據上述資訊跑一下單測

@Test
public void en() {
    int p = 3;
    int q = 5;
    int n = p * q;
    int z = (p - 1) * (q -1);
    int e = 7;
    int d = 15;

    int source = 13;
    System.out.println("原明文是： (" + source + ")");
    double pow = Math.pow(source, e);
    long result = (long) Math.abs(pow);
    System.out.println("加密計算的中間值：" + result);
    result = result % n;
    System.out.println("=======================================> 加密後的密文： " + result);

    // 以下開始解密
    double pow2 = Math.pow(result, d);
    long result2 = (long) Math.abs(pow2);
    System.out.println("解密計算的中間值：" + result2);
    result2 = result2 % n;
    System.out.println("=======================================> 解密後的明文： " + result2);
}

原明文是： (13)
加密計算的中間值：62748517
=======================================> 加密後的密文： 7
解密計算的中間值：4747561509943
=======================================> 解密後的明文： 13

我們為13加密，加密後的密文為7，可以成功解密並還原13；但是為了給13加解密，需要計算的代價可見一斑，其中解密的中間值達到了13位數4747561509943

注：這裡需要注意一點，明文的長度，一定不能超過n，因為加密的過程是明文階乘後對n取模，如果長度超過n，那就可能存在多個不同的明文對應一個密文，此時解密演演算法一定出現問題；另外還有個小細節，即明文、密文的長度是一個量級的，因為它們都是通過對n取模後得到，這樣使得破解難度進一步提高

2.3、原理推導

RSA加密雖然名字簡單，但是卻用到了很多經典的數學定理，接下來我們一步步推導一下

2.3.1、基礎定理

設定兩個大質數 p、q

n = p * q

因為n比較特殊，它是兩個質數的乘積，因此根據尤拉函數，可以很快的計算φ(n)

z = φ(n) = (p - 1) * (q - 1)

e 找到一個整數e，滿足如下條件

• e < n
• e 與 z 互質

由於e與z互質，根據貝祖等式，一定可以找到整數x、y，使得如下等式成立

e * x - z * y = 1

因此由於z = φ(n) = (p - 1) * (q - 1)，所以上述等式可以變形為

e * x = 1 + z * y = 1 + (p - 1) * (q - 1) * y

此時公鑰、私鑰也就誕生了

• 公鑰：(n, e)
• 私鑰：(n, x)

2.3.2、推導

有上文得知，加解密的公式如下：

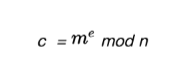
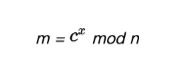
將加密公式帶入解密公式後，我們其實是得到了這樣一個新公式：

接下來就是推導這個等式是否成立了，如果這個公式成立，那麼我們也就推匯出了RSA

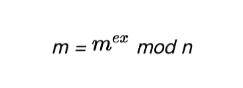
由上2.3.1章節，我們已經推匯出 ex = 1 + φ(n)*y，因此上述公式可變形為

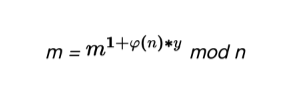
進而變形為

因為任何兩個數的乘積取模，都等於分別取模後相乘，因此可繼續變形

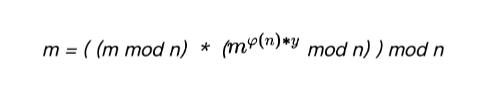
再簡單變一下形

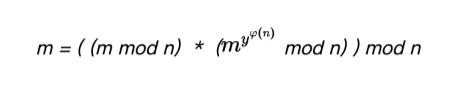
這裡m是我們需要加密的明文，它的大小遠小於n，而n則是兩個大質數的乘積，即n=p*q。因此可以保證m^y與n互質，此處就要用到費馬-尤拉定理了，即若n，a為正整數，且n，a互質，則: a^φ(n) ≡ 1 (mod n)

因此，上述公式馬上就可簡化

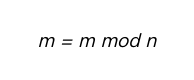
m為密文，因為我們加密的時候，對明文都是採取分段加密的方式，因此m都是小於n的，所以最終推匯出

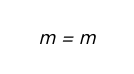
因此公式得證

2.4、加密實踐

"attack 9:00"

我們對上述明文進行加密；因為計算機底層所有的儲存都是二進位制的，因此將上述明文解析後可以得到一個byte陣列，拿到了byte陣列也即將其轉換為了二進位制數位

@Test
public void enBig() {
    BigInteger p = new BigInteger("1125899839733759");
    BigInteger q = new BigInteger("18014398241046527");
    BigInteger n = p.multiply(q);
    BigInteger z = p.subtract(BigInteger.valueOf(1)).multiply(q.subtract(BigInteger.valueOf(1)));
    BigInteger e = z.subtract(BigInteger.valueOf(1));
    BigInteger x = new BigInteger("20282408092494375639463130824708").add(new BigInteger("20282408092494375639463130824707"));

    System.out.println("p = " + p.toString());
    System.out.println("q = " + q.toString());
    System.out.println("n = " + n.toString());
    System.out.println("e = " + e.toString());
    System.out.println("z = " + z.toString());
    System.out.println("x = " + x.toString());

    String str = "attack 9:00";
    byte[] bytes = str.getBytes();
    BigInteger source = new BigInteger(1, bytes);

    System.out.println("原明文字串是： " + str);
    System.out.println("原明文轉換為10進位制後的數位為： " + source.toString());

    BigInteger c = source.modPow(e, n);
    System.out.println("=======================================> 加密後的密文： " + c);

    System.out.println("開始解密");
    BigInteger newSource = c.modPow(x, n);
    System.out.println("解密完成");
    String newSourceStr = new String(newSource.toByteArray(), StandardCharsets.UTF_8);
    System.out.println("=======================================> 解密後的10進位制數： " + newSource);
    System.out.println("=======================================> 解密後的字串為： " + newSourceStr);
}

p = 1125899839733759
q = 18014398241046527
n = 20282408092494394779761211604993
e = 20282408092494375639463130824707
z = 20282408092494375639463130824708
x = 40564816184988751278926261649415
原明文字串是： attack 9:00
原明文轉換為10進位制後的數位為： 117815745854514889615880240
=======================================> 加密後的密文： 4132881878846003477553871672250
開始解密
解密完成
=======================================> 解密後的10進位制數： 117815745854514889615880240
=======================================> 解密後的字串為： attack 9:00

上文中，我們隨便選取了兩個相對大的質數

• p = 1125899839733759
• q = 18014398241046527

其本質是需要保證p*q後的值，大於"attack 9:00"所代表的數位

因為p、q已經指定，那麼n、z也就固定了

• n = 20282408092494394779761211604993
• z = 20282408092494375639463130824708

e需要小於n，且與z互質，簡單起見，我們直接通過e = z - 1來選擇e

• e = z - 1 = 20282408092494375639463130824707

在需要滿足等式 e*x - z*y = 1 的前提下，我們隨便選取一個x滿足等式即可

• x = 40564816184988751278926261649415

其實通過JDK所帶的KeyPairGenerator來生成RSA的公私金鑰對兒時，也是上述的思路，不過生成的n值比較大，常見的有1024、2048、4097位。我們這個例子中的n值，不過也就100位左右，當然位數越多越安全，越難被破解

可見加密的代價是巨大的，一個簡單的"attack 9:00"字串後，是大量的cpu功耗

2.5、為什麼難破解

現在我們把自己想象成一個網路駭客，拿2.4舉例來說，對外暴露的公鑰是

• (n=20282408092494394779761211604993, e=20282408092494375639463130824707)

假如我們現在拿到了這樣一段密文

• 密文c = 4132881878846003477553871672250

我們只要進行如下運算就可以獲取明文

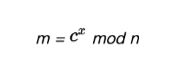
其中，n我們已經知道了，只需要拿到x就能直接破解，而x是通過公式「e*x - z*y = 1」推匯出來的，其中

• z = φ(n)
• e < n，且與z互質

而e作為公鑰中的一個屬性，已經完全對外暴露，我們現在只需要知道z(φ(n))的值，再套入公式「e*x - z*y = 1」中便可取得x的值，因為如果e、z、n都已經知道，那麼滿足這個等式的(x, y)是可窮舉的，也就成功破解RSA演演算法了

因此現在的矛盾直接指向了φ(n)，因為不知道p、q的具體內容，因此直接使用尤拉函數φ(n) = (p-1)(q-1)，但我們知道n，現在需要對其進行因數分解

• 也就是對 (n=20282408092494394779761211604993) 因數分解

對於這個問題可以先來個簡單的，比如：請嘗試求φ(77)，我們如果不知道它是由兩個質數相乘得到的話，只能從1開始逐一嘗試，這個破解難度可想而知。φ(77)={1,2,3,4,5,6,8,9,10,12,13,15,16,17,18,19,20,21,23,24,25,26,27,30,31,32,34,36,37,38,39,40,41,43,45,46,47,48,50,51,52,53,54,58,57,59,60,61,62,64,65,67,68,69,71,72,73,74,75,76}=60，如果知道77=11*7，即2個質數相乘的話，就很容易得到φ(77)=(11-1)*(7-1)=10*6=60

因此事實是，這個工作是災難性的，迄今為止，沒有一個高效的方法對一個大數進行因式分解，只能通過暴力搜尋的方式。我們這個例子中，n的值只取了100位，看上去就很難破解了，而實際應用中，通常都是2048位元或4096位，短時間內可以說無法破解