Codeforces Round #844 (Div.1 + Div.2) CF 1782 A~F 題解
A. Parallel Projection
我們其實是要在這個矩形的邊界上找一個點(x,y),使得(a,b)到(x,y)的曼哈頓距離和(f,g)到(x,y)的曼哈頓距離之和最小,求出最小值之後加h就是答案了,因為我們不可能在豎著的牆面上來回走,只可能走一次。進一步發現我們在上底面和下底面中,總有一個會走直線,也就是從起點沿直線直接走到邊界,然後沿著牆面往下或往上走。把這8種情況都列舉一遍即可(也可能4種就夠了,但是Div2A可沒有那麼多時間去想)。
時間複雜度\(O(1)\)。
點選檢視程式碼
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nEXECUTION TERMINATED";
#endif
exit(0);
}
using namespace std;
LL t,w,d,h,ans;
void upd(LL x,LL y,LL xx,LL yy,LL add)
{
ans=min(ans,llabs(x-xx)+llabs(y-yy)+add);
}
void upd(LL x,LL y,LL xx,LL yy)
{
upd(0,y,xx,yy,x);
upd(w,y,xx,yy,w-x);
upd(x,0,xx,yy,y);
upd(x,d,xx,yy,d-y);
}
int main()
{
fileio();
cin>>t;
rep(tn,t)
{
cin>>w>>d>>h;
LL x,y,xx,yy;
cin>>x>>y>>xx>>yy;
ans=1e18;
upd(x,y,xx,yy);upd(xx,yy,x,y);
printf("%lld\n",ans+h);
}
termin();
}
B. Going to the Cinema
先搞清楚題意,看看樣例解釋發現去0個人也是可以的。
假設現在強制恰好有x個人去。顯然\(a_i>x\)的人只能不去,\(a_i<x\)的人必須去。\(a_i=x\)的人,如果他去了,那除了他以外的去的人就是x-1,他就會不開心;如果不去,除了他以外的去的人就是x,他也會不開心;所以不允許這樣的人存在。因此列舉x,如果\(a_i<x\)的人數=x,且不存在\(a_i=x\)的人,就有1種方案,否則沒有方案。
時間複雜度\(O(n)\)。
點選檢視程式碼
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nEXECUTION TERMINATED";
#endif
exit(0);
}
using namespace std;
int t,n,a[200010],b[200010],c[200010];
int main()
{
fileio();
cin>>t;
rep(tn,t)
{
cin>>n;
rep(i,n+3) b[i]=c[i]=0;
rep(i,n)
{
cin>>a[i];
++b[a[i]];c[a[i]]=1;
}
rep(i,n+3) b[i+1]+=b[i];
int ans=0;
rep(go,n+1) if(b[go]==go&&c[go]==0) ++ans;
cout<<ans<<endl;
}
termin();
}
C. Equal Frequencies
先列舉t中字母的種類數cnt,那麼每種字母有\(len=\frac n{cnt}\)個。接下來我們要選出這cnt種字母,顯然選s中出現次數越多的越好。令\(c_i\)表示字母i在s中的出現次數。對於字母i,如果它是選出的cnt個之一,且\(cnt\le c_i\),就把這cnt個i都放到s中字母i出現的對應位置。剩下沒放的字母,發現不管怎麼放都至少會產生這麼多代價,所以隨便放即可。最後用構造出的字串更新一下答案就行了。
時間複雜度\(O(26n)\)。
點選檢視程式碼
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nEXECUTION TERMINATED";
#endif
exit(0);
}
using namespace std;
int t,n;
string s;
vector <int> v[30];
pair <int,string> ans;
int main()
{
fileio();
cin>>t;
rep(tn,t)
{
cin>>n>>s;
rep(i,28) v[i].clear();
rep(i,n) v[s[i]-'a'].pb(i);
vector <int> ord;rep(i,26) ord.pb(i);
sort(ord.begin(),ord.end(),[](int x,int y){return v[x].size()>v[y].size();});
ans=mpr((int)1e9,"");
repn(cnum,26) if(n%cnum==0)
{
int ecnt=n/cnum,dif=0;
string res="",lft="";rep(i,n) res.pb('-');
rep(j,cnum)
{
int use=min(ecnt,(int)v[ord[j]].size());
rep(k,use) res[v[ord[j]][k]]=ord[j]+'a';
rep(k,ecnt-use) lft.pb(ord[j]+'a');
}
dif=lft.size();
rep(j,res.size()) if(res[j]=='-')
{
res[j]=lft.back();
lft.pop_back();
}
ans=min(ans,mpr(dif,res));
}
cout<<ans.fi<<endl<<ans.se<<endl;
}
termin();
}
D. Many Perfect Squares
發現答案至少為1,我們只需要看答案>1的情況。如果答案>1,那肯定存在\(i,j(i<j)\),滿足存在x使得\(a_i+x,a_j+x\)都是完全平方數(注意a陣列遞增)。所以這就要求存在兩個數\(b,c\),使得\((b+c)^2-b^2=a_j-a_i\),也就是\(c^2-2bc=a_j-a_i\)。由於\(a_j-a_i\le 1e9\),所以對於任意合法的(b,c),\(c\le \sqrt{1e9}\)。因此我們可以列舉i和j,然後再列舉c,就可以求出所有滿足"a陣列中有至少兩個數+x之後為完全平方數"的x了。理論上界是1e8左右,實際上遠遠達不到。對每個求出的x,直接暴力求出它的squareness,判斷\(a_i+x\)的充要條件是\(((int)floor(sqrt(a_i+x)+0.5))^2=a_i+x\)。
時間複雜度\(O(能過)\)。
點選檢視程式碼
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nEXECUTION TERMINATED";
#endif
exit(0);
}
using namespace std;
LL t,n,a[60],ans;
void checkX(LL x)
{
LL res=0;
rep(i,n)
{
LL val=floor(sqrt(a[i]+x)+0.5);
if(val*val==a[i]+x) ++res;
}
ans=max(ans,res);
}
void check(LL i,LL sub)
{
for(LL N=1;N*N<sub;++N)
{
LL XN2=sub-N*N;
if(XN2%(N+N)==0)
{
LL sml=XN2/(N+N);sml*=sml;
if(sml>=a[i]) checkX(sml-a[i]);
}
}
}
int main()
{
fileio();
cin>>t;
rep(tn,t)
{
cin>>n;
rep(i,n) cin>>a[i];
ans=1;
rep(i,n) for(int j=i+1;j<=n;++j) check(i,a[j]-a[i]);
cout<<ans<<endl;
}
termin();
}
E. Rectangle Shrinking
思路不難,寫起來比較煩。這題的本質是大模擬。
直覺告訴我們:初始被任意一個矩形覆蓋的格子,在最後應該也一定能被覆蓋。問題就是怎麼構造出方案。
先把矩形分成三類:只在第一行的,只在第二行的,橫跨兩行的。然後對每一類的所有矩形的左端點和右端點都做一些調整(直接刪除也行),使得同一類中沒有任意兩個矩形有重合,且每一類中所有矩形的並保持原樣。這個直接排一下序就可以做到。
然後把只在第一行的,只在第二行的這兩類中調整完的矩形加入答案。接下來,向答案中逐個插入調整完的橫跨兩行的矩形。假設當前插入的橫跨兩行的矩形的左右端點分別為\(L,R\)。令條件1="當前答案中是否存在只在第一行的矩形i滿足\(l_i\le L且R\le r_i\)",條件2="當前答案中是否存在只在第二行的矩形i滿足\(l_i\le L且R\le r_i\)"。如果兩個條件都成立,那麼這個矩形已經沒有用了,可以刪除。如果只有條件1成立,那就強制把當前矩形變成只在第二行的矩形並加入答案;如果當前答案中已經有隻在第二行的矩形與這個矩形有重合,那就對這些矩形的左右邊界進行調整(或者直接刪除),使得所有原來被覆蓋的格子現在仍被覆蓋。只有條件2成立的情況同理。如果兩個條件都不成立,那就直接把這個矩形加入答案,然後調整答案中已有的與當前矩形有重合的矩形的左右邊界。以上操作都可以用set完成。容易發現在這種構造方式下,初始被任意一個矩形覆蓋的格子,在最後也一定能被覆蓋。
時間複雜度\(O(nlogn)\)。
點選檢視程式碼
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <LL,LL>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nEXECUTION TERMINATED";
#endif
exit(0);
}
using namespace std;
LL t,n,u[200010],d[200010],l[200010],r[200010];
set <pair <pii,LL> > st[3];//{雙,上,下}
void del(LL w,LL ll,LL rr)
{
if(st[w].empty()) return;
auto tmp=st[w].lower_bound(mpr(mpr(ll,0LL),0LL));
if(tmp!=st[w].begin())
{
--tmp;
if(tmp->fi.se>=ll)
{
auto val=*tmp;val.fi.se=ll-1;
st[w].erase(tmp);
st[w].insert(val);
}
}
while(true)
{
auto it=st[w].lower_bound(mpr(mpr(ll,0LL),0LL));
if(it==st[w].end()||it->fi.fi>rr) break;
if(it->fi.se<=rr) st[w].erase(it);
else
{
auto val=*it;val.fi.fi=rr+1;
st[w].erase(it);
st[w].insert(val);
}
}
}
bool isCovered(LL w,LL ll,LL rr)
{
if(st[w].empty()) return false;
auto tmp=st[w].lower_bound(mpr(mpr(ll,0LL),0LL));
if(tmp!=st[w].begin())
{
--tmp;
if(tmp->fi.se>=rr) return true;
}
auto it=st[w].lower_bound(mpr(mpr(ll,0LL),0LL));
if(it!=st[w].end()&&it->fi.fi==ll&&it->fi.se>=rr) return true;
return false;
}
int main()
{
fileio();
cin>>t;
rep(tn,t)
{
scanf("%lld",&n);
rep(i,n) scanf("%lld%lld%lld%lld",&u[i],&l[i],&d[i],&r[i]);
rep(i,3) st[i].clear();
vector <pair <pii,LL> > tmp;
rep(i,n) if(d[i]==1) tmp.pb(mpr(mpr(l[i],r[i]),i));
sort(tmp.begin(),tmp.end());
int mx=0;
rep(i,tmp.size())
{
if(mx>=tmp[i].fi.se) continue;
if(tmp[i].fi.fi>mx)
{
mx=tmp[i].fi.se;
st[1].insert(tmp[i]);
}
else
{
st[1].insert(mpr(mpr(mx+1,tmp[i].fi.se),tmp[i].se));
mx=tmp[i].fi.se;
}
}
tmp.clear();
rep(i,n) if(u[i]==2) tmp.pb(mpr(mpr(l[i],r[i]),i));
sort(tmp.begin(),tmp.end());
mx=0;
rep(i,tmp.size())
{
if(mx>=tmp[i].fi.se) continue;
if(tmp[i].fi.fi>mx)
{
mx=tmp[i].fi.se;
st[2].insert(tmp[i]);
}
else
{
st[2].insert(mpr(mpr(mx+1,tmp[i].fi.se),tmp[i].se));
mx=tmp[i].fi.se;
}
}
vector <pair <pii,LL> > addord;
tmp.clear();
rep(i,n) if(u[i]==1&&d[i]==2) tmp.pb(mpr(mpr(l[i],r[i]),i));
sort(tmp.begin(),tmp.end());
mx=0;
rep(i,tmp.size())
{
if(mx>=tmp[i].fi.se) continue;
if(tmp[i].fi.fi>mx)
{
mx=tmp[i].fi.se;
st[0].insert(tmp[i]);addord.pb(tmp[i]);
}
else
{
st[0].insert(mpr(mpr(mx+1,tmp[i].fi.se),tmp[i].se));addord.pb(mpr(mpr(mx+1,tmp[i].fi.se),tmp[i].se));
mx=tmp[i].fi.se;
}
}
st[0].clear();
rep(ii,addord.size())
{
int i=addord[ii].se;l[i]=addord[ii].fi.fi;r[i]=addord[ii].fi.se;
bool c1=isCovered(1,l[i],r[i]),c2=isCovered(2,l[i],r[i]);
if(c1&&c2) continue;
if(c2)
{
del(1,l[i],r[i]);
st[1].insert(mpr(mpr(l[i],r[i]),i));
}
else if(c1)
{
del(2,l[i],r[i]);
st[2].insert(mpr(mpr(l[i],r[i]),i));
}
else
{
del(1,l[i],r[i]);del(2,l[i],r[i]);
st[0].insert(mpr(mpr(l[i],r[i]),i));
}
}
rep(i,n) l[i]=r[i]=u[i]=d[i]=0;
for(auto it:st[0])
{
int id=it.se;
u[id]=1;d[id]=2;l[id]=it.fi.fi;r[id]=it.fi.se;
}
for(auto it:st[1])
{
int id=it.se;
u[id]=1;d[id]=1;l[id]=it.fi.fi;r[id]=it.fi.se;
}
for(auto it:st[2])
{
int id=it.se;
u[id]=2;d[id]=2;l[id]=it.fi.fi;r[id]=it.fi.se;
}
LL ans=0;
rep(i,n) if(u[i]!=0) ans+=(d[i]-u[i]+1)*(r[i]-l[i]+1);
cout<<ans<<endl;
rep(i,n) printf("%lld %lld %lld %lld\n",u[i],l[i],d[i],r[i]);
}
termin();
}
F. Bracket Insertion
發現一旦在中途的某步操作時使得這個括號序列不合法了,那之後就再也救不回來了,因為如果把(看成1,)看成-1,不管插入()還是)(都不能再改變某個字元處的字首和,而括號序列合法的充要條件就是每個字元處的字首和\(\ge 0\)。
我們的每次插入操作都是均等概率地選擇一個間隔,並插入一些東西。每次操作都會增加恰好2個間隔。定義一個間隔的權值為它前面所有括號的權值和("("為1,")"為-1)。令p=插入()的概率,q=1-p。則操作的過程可以轉化成這樣:有一個多重集,初始為\(\{0\}\),一共進行n次操作,每次均等概率地從中選擇一個數x,並以p的概率插入\(\{x,x+1\}\),以q的概率插入\(\{x,x-1\}\),求最後多重集中不存在負數的概率。
我們可以把多重集中的每個數看成有根樹上的一個節點。這棵樹點和邊都有權值,第i次操作時我們在樹上隨機選擇一個節點,並給它增加兩個兒子,其點權都為i。兩個兒子其中一個到父親的邊權為0,另一個邊權以p的概率為1,q的概率為-1。求樹上沒有任意一個節點到根的權值和為負數的概率。
為了便於理解,我們把"求概率"改為"對合法的樹形態計數"(每條非零邊值為1的"方案數"為p,為-1的"方案數"為q,因為概率和方案數本來就是差不多的東西)。最後我們只要把這個方案數除以\(1\cdot3\cdot5\cdots (2n-1)\)就是答案。注意這個樹上每個節點的兒子之間是沒有順序的。
為了方便計數,我們修改一下樹的結構。初始樹上有一個關鍵點。第i次操作時,選一個關鍵點,在它的下面連上這樣一個東西:
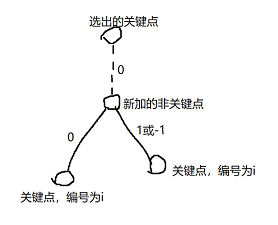
接下來就可以dp了。
- \(dp_{i,j}\)表示一個關鍵點個數為2i-1(包括根)的子樹,根為關鍵點,子樹中關鍵點權值在[1,i-1]中,最終整棵樹的根到這個子樹的根的邊權和為j,子樹內沒有到整棵樹的根的邊權和為負的節點的方案數。最終答案為\(dp_{n+1,0}\)。
- \(g_{i,j}\)表示一個關鍵點個數為2i的子樹,根為非關鍵點,子樹中關鍵點權值在[1,i]中,最終整棵樹的根到這個子樹的根的邊權和為j,子樹內沒有到整棵樹的根的邊權和為負的節點的方案數。
來看看怎麼對\(dp_{i,j}\)轉移,我們需要列舉它的每個子樹的大小,並給每個子樹中的關鍵點分配權值(是一個多重組合數),還要去重(因為子樹之間沒有順序)。看起來非常麻煩,所以我們定義一個輔助陣列\(f_{i,j}\),使得\(dp_{i,j}=f_{i-1,j}\cdot (i-1)!\)。
我們從小到大地列舉i,在求出\(dp_{i,*}\)的同時維護f。列舉三個數j,k和cnt,從\(f_{j,k}\)轉移到\(f_{j+cnt\cdot i,k}\)。cnt這一維的複雜度是個調和級數,所以總的列舉量是\(O(n^3logn)\)。轉移係數是\(\frac 1{(cnt\cdot i)!}g_{i,k}^{cnt}\cdot \binom{i\cdot cnt-1}{i-1}\cdot \binom{i(cnt-1)-1}{i-1}\cdots \binom{i-1}{i-1}\)。其中最前面的\(\frac 1{(cnt\cdot i)!}\)與上面的\(dp_{i,j}=f_{i-1,j}\cdot (i-1)!\)中的\((i-1)!\)構成一個多重組合數,用來把i-1種點權分散到每種\(g_{i,k}\);後面的一連串組合數是用來把\(i\cdot cnt\)種點權分散到\(cnt\)個\(g_{i,k}\),由於兒子之間無序,所以用每次選出當前沒選的最小權值所在的子樹中的所有權值的方式來計數。
\(g\)的轉移很簡單,在列舉到i時,列舉三個數j,k和r使得j、k中有至少一個=i,並把\(dp_{j,r}\cdot(dp_{k,r+1}\cdot p+dp_{k,r-1}\cdot q)\)轉移到\(g_{j+k-1,r}\)即可。還需要乘上一個分配點權的組合數。
總時間複雜度\(O(n^3logn)\)。有點卡常,要儘量減少最內層迴圈的計算量。
點選檢視程式碼
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define repn(i,n) for(int i=1;i<=n;++i)
#define LL long long
#define pii pair <int,int>
#define fi first
#define se second
#define mpr make_pair
#define pb push_back
#pragma GCC optimize("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,avx2,tune=native")
#pragma GCC optimize("inline","fast-math","unroll-loops","no-stack-protector")
void fileio()
{
#ifdef LGS
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
}
void termin()
{
#ifdef LGS
std::cout<<"\n\nEXECUTION TERMINATED";
#endif
exit(0);
}
using namespace std;
const LL MOD=998244353;
LL qpow(LL x,LL a)
{
LL res=x,ret=1;
while(a>0)
{
if(a&1) (ret*=res)%=MOD;
a>>=1;
(res*=res)%=MOD;
}
return ret;
}
LL n,p,q,dp[510][510],fac[1010],inv[1010],rinv[1010],f[510][510],g[510][510],c[1010][1010];
LL C(LL nn,LL mm){return fac[nn]*inv[mm]%MOD*inv[nn-mm]%MOD;}
void calcG(int i,int j)
{
LL toi=i+j-1,mul=C(i-1+j-1,i-1);
if(toi>=n+3) return;
rep(k,n+2)
{
LL val=dp[i][k]*((dp[j][k+1]*p+(k==0 ? 0LL:dp[j][k-1]*q))%MOD)%MOD;
(g[toi][k]+=val*mul)%=MOD;
}
}
int main()
{
fileio();
fac[0]=1;repn(i,1005) fac[i]=fac[i-1]*i%MOD;
rep(i,1003) inv[i]=qpow(fac[i],MOD-2),rinv[i]=qpow(i,MOD-2);
cin>>n>>p;
(p*=qpow(10000,MOD-2))%=MOD;q=(1-p+MOD)%MOD;
rep(i,n+3) rep(j,i+1) c[i][j]=C(i,j);
rep(i,n+3) f[0][i]=1;
repn(i,n+1)
{
if(i==1) rep(j,n+3) dp[i][j]=1;
else
{
rep(j,n+2)
dp[i][j]=f[i-1][j]*fac[i-1]%MOD;
}
repn(j,i)
{
int k=i;
calcG(j,k);
}
repn(k,i-1)
{
int j=i;
calcG(j,k);
}
for(int pre=n;pre>=0;--pre) rep(j,n+2) if(f[pre][j])
{
LL mul=1;
for(int cnt=1;pre+cnt*i<=n;++cnt)
{
(mul*=g[i][j]*c[i*cnt-1][i-1]%MOD)%=MOD;
LL rv=mul*inv[cnt*i]%MOD;
(f[pre+cnt*i][j]+=f[pre][j]*rv)%=MOD;
}
}
}
LL ans=dp[n+1][0];
repn(i,n) (ans*=qpow(i*2-1,MOD-2))%=MOD;
cout<<ans<<endl;
termin();
}