【Machine Teaching】An Overview of Machine Teaching
Machine Teaching
1 Introduction
1️⃣ 什麼是 Machine Teaching?
searching the optimal (usually minimal) teaching set given a target model and a specific learner
學生可以類比為機器學習演演算法,老師知道學生的演演算法以及引數,並且知道學生模型引數的最優值,但是不能直接告訴學生,而是構造最優的訓練集讓學生訓練,使得學生的引數儘可能達到該最優值。
2️⃣ 如何定義最優?
一般的,訓練集基數越小越好。
3️⃣ 如果老師已經知道了最優引數,為什麼還要費勁去訓練學生學會呢?
該問題在第二章中有解釋。老師和學生是獨立的個體,不能發生心電感應,有些時候只能通過訓練資料向學生傳遞最優引數資訊。在一些場景,比如訓練集中毒的網路安全問題上以及圖片型別識別上有所體現。
4️⃣ 為什麼說機器教學是機器學習的逆過程?
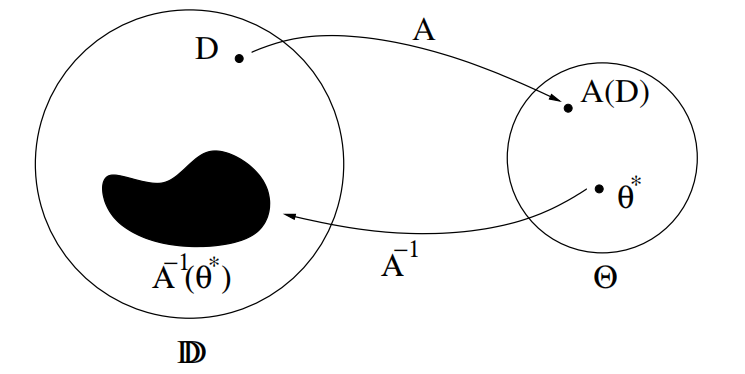
機器學習是學生利用給定的訓練資料 \(D\) ,在演演算法 \(A\) 上進行訓練,得到訓練結果 \(A(D)\),該結果表示模型中的引數取值。
機器教學是老師利用已知的最優模型引數,在演演算法 \(A\) 的逆運算上反向得到最優的訓練資料。
5️⃣ 如何求解訓練集
不會去求 \(A\) 的逆,而是轉化成優化問題。
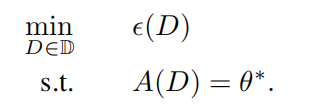
- \(\epsilon(D)\):teaching effort function,大小一般與訓練集基數相等,越小越好。也可以給其增加更復雜的含義,比如分類問題中不同類之間的距離。
- $\mathbb{D} $:訓練集的搜尋空間。比如在 pool-based machine teaching 中,池子包含資料集 \(S\) ,訓練集資料只能從池子裡面選擇,即只能是 \(S\) 的一個子集,搜尋空間表示池子中資料的所有可能組合情況,即 \(2^S\)。
冪集:設有集合A,由A的所有子集組成的集合,稱為A的冪集,記作 \(2^A\),即:\(2^A=\left\{ S|S\subseteq A \right\}\) 。
6️⃣ 如果機器學習演演算法沒有閉合解?
閉合解:closed-form expression 是一個數學表示式;這種數學表示式包含有限個標準運算。
對於大多數學生,沒有閉合形式的 \(A(D)\),沒法通過公式直接計算,大部分機器學習演演算法求解是基於最佳化
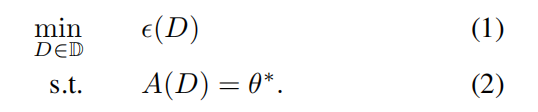
所以一般將 \(A(D)\) 表示成最佳化的形式,即二維優化問題:
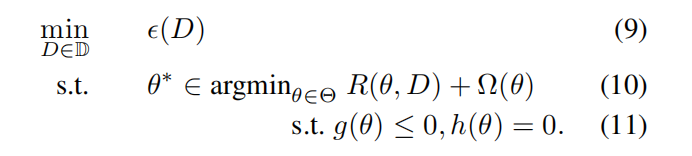
- \(R\) :經驗風險
- $\varOmega $ :正則化項
- \(g,h\):約束
二維優化問題難解,對於某些凸的機器學習演演算法,可以將(10)轉化成KKT條件,這樣的話下式就變成了上式的一些新的約束,二維優化就轉化為了一維優化問題。
(2)式和(10)式這兩個約束可能過於嚴格,很難滿足。
一個解決方法就是放鬆教學的約束,(1)式等價於
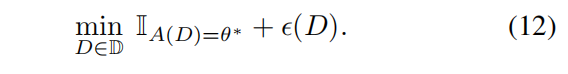
其中
如果學生正確學習到了 \(\theta^*\) ,值為 0;否則值為 \(\infty\) 。
可以放鬆這個約束,學生不用非得精確地學習到 \(\theta^*\) ,將(1)式放鬆為:
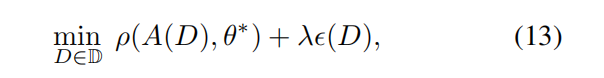
- \(\lambda\):調節
teaching risk和teaching effort的權重。 - $\rho \left( \right) $ :
teaching risk,用來衡量 \(A(D)\) 與 \(\theta^*\) 之間的差異。迴歸問題可以使用範數,分類問題可以定義如下:
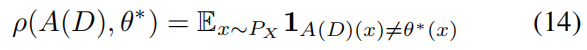
這樣放鬆二維優化問題得到下式:
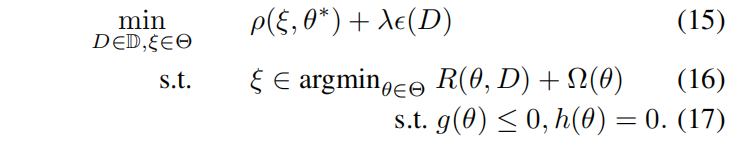
7️⃣ 老師是否能知道學生的演演算法的一切呢?
如果學生是人類,老師就無法知道學生的想法了。
有一種情況是,學生的演演算法屬於一類演演算法的集合 $A\in \mathbb{A} $ ,老師只知道 $\mathbb{A} $ 。一個解決方法就是通過 probe ,老師從一個初始訓練集 \(D_0\) 開始,學生進行訓練,但是老師不能直接觀察學生訓練後的模型 \(A(D_0)\),老師可以給學生資料讓其預測結果,對於 $A'\in \mathbb{A} $,只要 $A'\left( D_0 \right) \left( X \right) \ne A\left( D_0 \right) \left( X \right) $ ,就可以把 \(A'\) 剔除,最後集合中剩下的一個演演算法就是學生的演演算法。
Example1: 1D threshold classifier
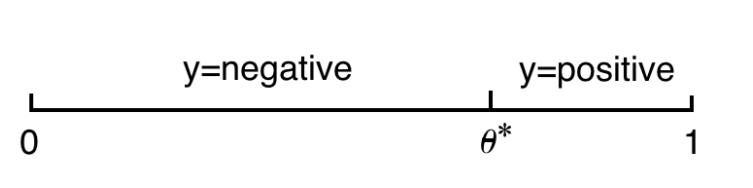 $$
y=\begin{cases}
positive,x>\theta ^*\\
negative,x<\theta ^*\\
\end{cases}
$$
輸入 $n$ 個獨立同分布且服從 $0-1$ 分佈的訓練資料進行訓練。
$$
y=\begin{cases}
positive,x>\theta ^*\\
negative,x<\theta ^*\\
\end{cases}
$$
輸入 $n$ 個獨立同分布且服從 $0-1$ 分佈的訓練資料進行訓練。
Passive learning
泛化誤差:
這是因為 \(n\) 個獨立同分布且服從 \(0-1\) 分佈的訓練資料的平均間隔是 \(1/n\) ,代表了決策邊界的不確定性區間大小。
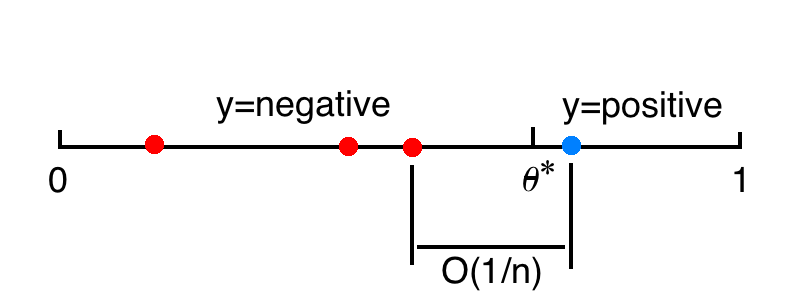
如果想要控制泛化誤差為 \(0.001\),就需要令 \(n=1000\)。
簡單來說,被動學習中,學生僅僅接受知識,而不進行提問。學生對於訓練資料只知道它們的標籤應該是什麼,而該分類問題的關鍵是距離 \(\theta^*\) 最近的靠近 0 端和靠近 1 端的兩個資料,其他訓練資料沒有用處。
Active learning
泛化誤差:
主動學習是一個二分檢索的過程,學生會向老師提問,老師回答目標 \(\theta\) 的答案,每次淘汰一半的資料。
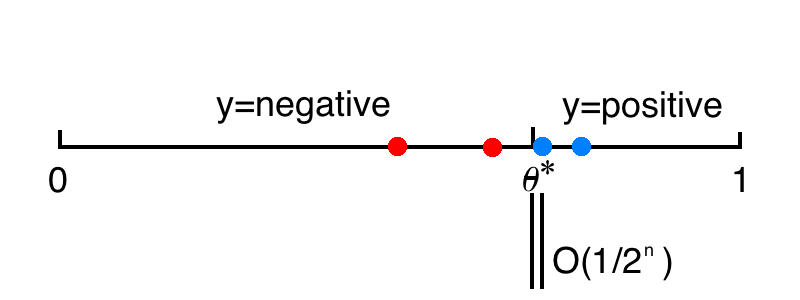
如果想要控制泛化誤差為 \(0.001\),只需要令 \(n=10\)。
簡單來說,主動學習中,學生不僅接受知識,而且對老師進行提問,老師進行解答。
Machine teaching
老師知道目標引數 \(\theta^*\) ,如果想要泛化誤差為 $\epsilon $ ,只需要提供兩個訓練資料,一個在 \(\theta^*\) 左邊,一個在 \(\theta^*\) 右邊,兩個訓練資料之間的距離是 $\epsilon $ ,而 $\theta^* $ 位於中間即可。
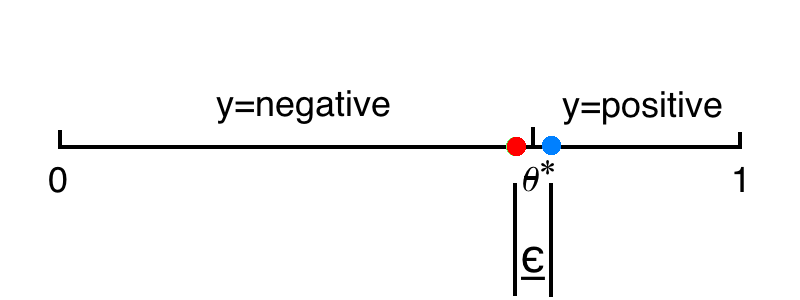
簡單來說,機器教學中,老師知道最優引數以及學生的模型和引數,並且會由此設計最優的訓練集用來訓練學生,使得學生引數儘可能達到最優引數。
Example2: SVM
老師想要教給學生 SVM d 維空間超平面決策邊界,只需要提供兩個訓練資料,分別位於超平面兩側被平面平分且連線垂直於超平面,這樣的點可以有無數種組合。
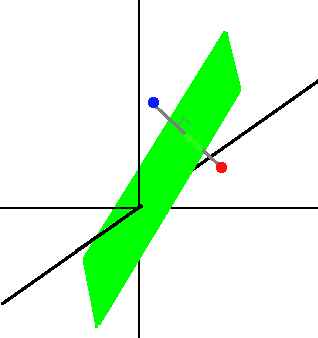
Example3: Gaussian density
對於 d 維高斯密度,
學生通過計算樣本均值和樣本協方差矩陣來學習。
老師可以用 \(d+1\) 個點構造訓練集,這些點是以 \(\mu\) 為中心的 \(d\) 維四面體頂點,且進行適當縮放。
Contrast
機器學習就是計算經驗風險取到最小值時的引數。
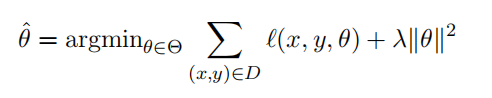
對於機器教學,目標引數 \(\theta^*\) 是已知的,老師需要找到一個訓練集,使得學生在該訓練集上訓練能夠得到損失函數最小時的引數接近 \(\theta^*\) 。
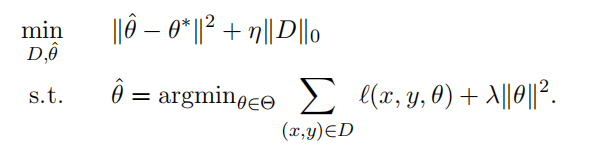
上式優化是老師的問題,老師需要關注學生學習情況,即 \(\hat{\theta}\) 是否接近 \(\theta^*\) ,同時還需要控制訓練集的大小,使用盡量小的訓練集。
下式優化是學生的機器學習問題。
老師需要知道學生的演演算法來構造優化。
2 Why bother if the teacher already knows \(\theta^*\) ?
有時候老師已經知道了 \(\theta^*\) ,那機器教學還有什麼意義?有的老師需要通過訓練資料來向學生傳達 \(\theta^*\) 。
- 地質學家知道如何判斷岩石型別,這個決策邊界 \(\theta^*\) 存放在老師那裡,沒法通過心靈感應直接傳遞給學生,但是老師可以通過挑選合適的岩石標本給學生展示,如果挑選的岩石標本代表性足夠強,學生就可以很快學會。利用機器教學可以優化岩石樣本的選擇。
- 訓練集中毒。 考慮一個垃圾郵件過濾器,它不斷調整它的閾值以適應。隨著時間的推移,合法內容的變化。知道該演演算法的攻擊者可以向垃圾郵件過濾器傳送專門設計的電子郵件,以操縱閾值,從而使某些垃圾郵件能夠通過濾器。在這裡,攻擊者扮演的是老師的角色,而受害者則是毫無戒心的學生。

從編碼的角度,老師有 \(\theta^*\) 的資訊,解碼者是一個固定的機器學習演演算法,它接受訓練集,將其解碼求得 \(A(D)=\hat{\theta}\) 。老師必須使用由訓練集組成的碼字對 \(\theta^*\) 編碼,最合適的碼字就是機器學習演演算法的逆。老師會在最小的訓練集挑選資料。
老師假定需要知道學生的機器學習演演算法。例如,學生是線性迴歸最小二乘法,老師給的訓練集也是按照符合該演演算法的資料,則可以訓練。但如果學生是帶正則項的嶺迴歸,老師原來的訓練集就不再適用了。
優化資料就是機器教學,而優化模型就是機器學習。
機器教學更正規的定義:
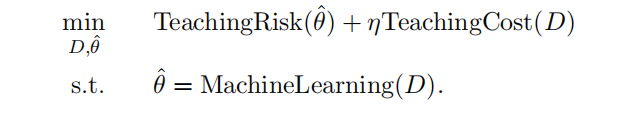
TeachingRisk:定義了老師的不滿意程度, \(\theta^*\) 包含在該方程中。也可以被定義為 \(\hat{\theta}\) 在驗證集上的泛化誤差,這時不需要 \(\theta^*\) 。TeachingCost:與訓練集大小有關。考慮訓練集對學生的負擔。
兩種受限的機器教學問題模式:
1️⃣ 在充分學習的前提下,儘量減少 TeachingCost。
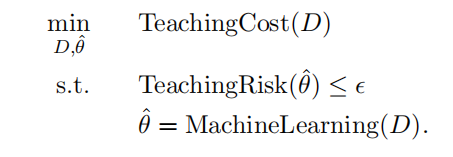
2️⃣ 優化學習,允許一定的 TeachingCost。

3 Characterizing the machine teaching space
3.1 The human vs. machine dimension: Who teaches whom?
機器教學空間的幾個不同維度。
- 機器教機器。資料中毒攻擊:老師的訓練集給出細微的修改,可以避免被檢測到,使得學生通過機器學習不斷學習中毒樣本。
- 機器教人。機器教學系統:類比之前的地理教學。
- 人教機器。人類領域專家用來快速訓練文字分類器。學生也可以教老師如何教學。
- 人教人。增強教育學。
3.2 The teaching signal dimension: What can the teacher use?
監督學習中使用帶標籤的資料。
synthetic / constructive teaching:使用特徵空間中的任意資料,並且對資料進行加工和構造。pool-based teaching:使用實際資料,比如影象和檔案。從池子裡面選擇資料。hybrid teaching:從池子裡選擇資料,還可以對資料進行修改。
3.3 The batch vs. sequential dimension: Teaching with a set or a sequence?
batch teaching:給學生一批無序資料學習。sequential teaching:老師必須優化訓練資料的順序,使得學生學習有序資料(由易到難)。
3.4 The model-based vs. model-free dimension: How much does the teacher know about the student?
model-based approach:老師知道學生的學習演演算法、引數、版本空間,學生對老師完全透明。model-free approach:學生對老師是黑盒,老師給學生訓練資料,只觀察學生輸出的TeachingRisk。gray box student:老師知道學生的學習演演算法的一部分,比如使用的什麼模型,什麼損失函數,但是可能不知道損失函數中的某些引數。老師可以probe學生,通過學生的結果推測引數值。
3.5 The student awareness dimension: Does the learner know it is being taught?
大多數機器教學場景是學生沒有預料到被訓練,學生認為的訓練資料是獨立同分布,而老師提供的訓練資料一般不是獨立同分布。
有一些場景中學生意識到了自己在被老師教
Recursive Teaching Dimension (RTD) and Preference-based Teaching Dimension (PBTD)- 學生可以提高老師的訓練集水平
- 如果老師心中學生的模型與學生實際的模型不一樣,學生意識到了這點,那麼學生可以調整老師提供的訓練資料使其符合自己的模型來實現最佳化
- 在安全領域,受害者可以使用防禦機制
3.6 The one vs. many dimension: how many students are simultaneously taught?
一個老師面對多個學生的情況,每個學生的學習演演算法可能都不一樣,老師不可能對每個學生都進行最好的教學。
一個選擇是優化最差的學生
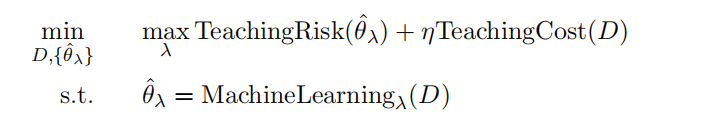
另一個選擇是優化平均學生

3.7 The angelic vs. adversarial dimension: Is the teacher a friend or foe?
根據意圖,機器教學有好有壞。
Reference
- Xiaojin Zhu, Adish Singla, Sandra Zilles, Anna N. Rafferty. An Overview of Machine Teaching. ArXiv 1801.05927, 2018.
- Xiaojin Zhu. Machine Teaching: an Inverse Problem to Machine Learning and an Approach Toward Optimal Education. In The Twenty-Ninth AAAI Conference on Artificial Intelligence (AAAI ``Blue Sky'' Senior Member Presentation Track), 2015. AAAI / Computing Community Consortium "Blue Sky Ideas" Track Prize.
An overview of machine teaching.
[pdf | talk slides]