演演算法學習筆記(8.1): 網路最大流演演算法 EK, Dinic, ISAP
網路最大流
前置知識以及更多芝士參考下述連結
網路流合集連結:網路流
最大流,值得是在不超過管道(邊)容量的情況下從源點到匯點最多能到達的流量
抽象一點:使 \(\sum_{(S, v) \in E} f(S, v)\) 最大的流函數被稱為網路的最大流,此時的流量被稱為網路的最大流量
有了最大流量,就可以通過奇奇怪怪的建模解決很多令人摸不著頭腦的題
例如二分圖:
對於一張二分圖,經過建模之後我們可以這樣畫
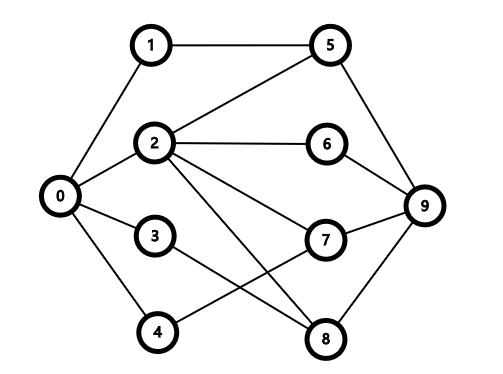
其中左部點集 \(A = \{1, 2, 3, 4\}\),右部點集 \(B = \{5, 6, 7, 8\}\), 其中源點為 \(0\),匯點為 \(9\)
建模過程:
新增一個源點 \(S\) 和一個匯點 \(T\), 從 \(S\) 到每一個左部點連有向邊,從每一個右部點到 \(T\) 連有向邊,把原二分圖的每條邊看作從左部點到右部點的有向邊,形成了一張 \(n + 2\) 個點 \(n + m\) 條邊的網路。其中每一條邊的容量都為 \(1\)。
不難發現,二分圖的最大匹配數就等於網路的最大流量。求出最大流後,所有有有」流「經過的點,邊就是匹配點,匹配邊。
進一步的:如果要求二分圖多重匹配,依據題目資訊改變連線匯點和源點的邊的容量即可
計算最大流的演演算法很多,這裡主要講解 \(EK (Edmonds-Karp)\) ,\(Dinic\) 和 \(ISAP\) 演演算法。
EK 增廣路演演算法
這裡的增廣路與二分圖裡面的增廣路有不一樣了 Q^Q
增廣路:若一條源點 \(S\) 到 \(T\) 的路徑上各邊的剩餘容量都嚴格大於 \(0\),則稱這條路徑為增廣路。顯然,可以讓一個流沿著增廣路流過,使得網路的流量增大。
而\(EK\)的思路就是不斷進行廣度優先搜尋尋找增廣路,直到不存在增廣路為止。
而在搜尋的時候,我們只考慮圖中所有 \(f(x, y) < c(x,y)\) 的邊(或者說是有剩餘容量的邊)。在尋找路徑的同時,還要記錄其前驅結點以及路徑上的最小容量\(minf\), 在找到一條增廣路後,則網路的流量可以增加 \(minf\)。
但是,考慮到斜對稱的性質,由於我們需要把增廣路上的所有邊的剩餘容量 \(e(u, v)\) 減去\(minf\),所以要在對其反邊容量 \(e(v, u)\) 加上 \(minf\)。
初始化的時候,如果是有向邊 \((u, v)\),則 \(e(u, v) = c(u, v), e(v, u) = 0\),如果是無向邊,則 \(e(u, v) = e(v, u) = c(u, v)\)。
?: 為什麼會出現無向邊,網路流不是有向圖嗎?
考慮雙向道路
馬路,既可以順流,又可以逆著。例如:[ICPC-Beijing 2006] 狼抓兔子 - 洛谷
這道題需要用到最小割,順便說一下,最小割 = 最大流
?: 為什麼使用BFS,而不是DFS?
因為DFS可能會繞圈圈……在講述DInic的時候我會再提及
複雜度:複雜度上界為 \(O(nm^2)\),然而實際上遠遠達不到這個上界,效率還行,可以處理 \(10^3 \sim 10^4\) 規模的網路
--《演演算法競賽進階指南》
我不會證明,下面的兩個演演算法也不會 Q^Q
這裡給出一種參考程式碼
提交記錄:記錄詳情
#include <iostream>
#include <cstring>
#include <algorithm>
#include <deque>
using std::deque;
const int N = 2e3 + 7, M = 5e5 + 7, INF = 0x7F7F7F7F;
int n, m, s, t;
int to[M], nex[M], wi[M] = {INF};
int head[N], tot = 1;
void add(int u, int v, int w) {
to[++tot] = v, nex[tot] = head[u], wi[tot] = w, head[u] = tot;
}
void read() {
scanf("%d %d %d %d", &n, &m, &s, &t);
int u, v, w;
for (int i = 0; i < m; ++i) {
scanf("%d %d %d", &u, &v, &w);
add(u, v, w);
add(v, u, 0);
}
}
#define min(x, y) ((x)<(y)?(x):(y))
#define pop() que.pop_front()
#define top() que.front()
#define push(x) que.push_back(x);
#define empty() que.empty()
static int inq[N], it = 0;
// px記錄上一個點,pe記錄遍歷過來的邊
static int px[N], pe[N];
inline int bfs() {
deque<int> que;
push(s); inq[s] = ++it;
int x, y;
while (!empty()) {
x = top(); pop();
for (int i = head[x]; i; i = nex[i]) {
if ((inq[(y = to[i])] ^ it) && wi[i]) {
px[y] = x, pe[y] = i;
if (y == t) return 1; // 找到增廣路了,
inq[y] = it; push(y);
}
}
}
return 0; // 到不到了,沒有增廣路了
}
void work(long long & res) {
while (bfs()) {
int val = INF;
for (int x = t; x ^ s; x = px[x]) {
val = min(val, wi[pe[x]]);
}
for (int x = t; x ^ s; x = px[x]) {
wi[pe[x]] -= val;
// 處理反邊的時候利用了成對變換的方法!
wi[pe[x] ^ 1] += val;
}
res += val;
}
}
int main() {
read();
long long res = 0;
work(res);
printf("%lld\n", res);
return 0;
}
Dinic
考慮到 \(EK\) 演演算法每一次在殘量網路上只找出來的一條增廣路,太慢了,所以有了更優化的東西 Dinic?歌姬吧
先引入一點點概念:
深度:在搜尋樹上的深度(BFS搜尋時的層數)
殘量網路:網路中所有節點以及剩餘容量大於 \(0\) 的邊構成的子圖
分層圖:依據深度分層的一段段圖……或者說在殘量網路上,所有滿足 \(dep[u] + 1 = dep[v]\) 的邊 \((u, v)\) 構成的子圖。
分層圖顯然是一張有向無環圖
Dinic 演演算法不斷重複下述過程,直到在殘量網路中,\(S\) 不能到達 \(T\)
-
利用BFS求出分層圖
-
在分層圖上DFS尋找增廣路,在回溯的時候實時更新剩餘容量。另外,每個點可以同時流出到多個結點,每個點也可以接收多個點的流。
?: 這裡為什麼可以使用DFS
由於我們分了層,意味著DFS只會向更深的地方搜尋,而不會在同一層亂跳,甚至搜尋到前面。這也是為什麼EK用BFS更優秀
複雜度:一般來說,時間複雜度為 \(O(n^2m)\),可以說是不僅簡單,而且容易實現的高翔演演算法之一,一般能夠處理 \(10^4 \sim 10^5\) 規模的網路。特別的,用此演演算法求二分圖的最大匹配時只需要 \(O(m\sqrt{n})\), 實際上表現會更好。
題目不變
沒有當前弧優化:提交詳情
有當前弧優化:記錄詳情
// 重複內容已省略
int dis[N], vis[N], vt = 0;
int now[N]; // 用於當前弧優化
// return true if exists non-0 road to t
bool bfs() {
memset(dis, 0, sizeof(dis)); dis[s] = 1;
deque<int> que;
que.push_back(s);
while (que.size()) {
int x = que.front(); que.pop_front();
now[x] = head[x]; // 更新當前弧
for (int y, i = head[x]; i; i = nex[i]) {
if (!dis[y = to[i]] && wi[i]) {
dis[y] = dis[x] + 1;
que.push_back(y);
if (y == t) return true;
}
}
}
return false;
}
#define min(x, y) ((x) < (y) ? (x) : (y))
long long dinic(int x, long long maxflow) {
if (x == t) return maxflow;
long long rest = maxflow, k;
for (int y, i = now[x]; i && rest; i = nex[i]) {
now[x] = i; // 更新當前弧
// 要在更深的一層,以及需要有剩餘流量
if (dis[y = to[i]] == dis[x] + 1 && wi[i]) {
k = dinic(y, min(rest, wi[i]));
if (!k) dis[y] = 0;
wi[i] -= k, wi[i ^ 1] += k;
rest -= k;
}
}
return maxflow - rest;
}
int main() {
read();
long long maxflow = 0, flow;
while (bfs()) {
while (flow = dinic(s, INF)) maxflow += flow;
}
printf("%lld\n", maxflow);
}
?: 當前弧優化是個啥玩意
注意到如果我們每一次遍歷後,對於當前邊 \((u, v)\),不可能再有流量流過這條邊,所以我們可以暫時的刪除這條邊……注意,只是暫時,每一分層的時候是需要考慮這條邊的,因為這條邊的剩餘流量不一定為 0
ISAP
某位大佬的部落格上說這是究極最大流演演算法之一。還有一個HLPP(最高標記預留推進),思路完全與這幾個方法不同,不依賴於增廣路,我會把它放在另外的文章中單獨講。
我可不會告訴你們是我不會優化,太笨了,看不懂大佬的優化這是我的:記錄詳情 4.77s
這是大佬的:記錄詳情 185ms
由於Dinic需要多次BFS……所以有些不滿足的數學家決定優化常數……於是有了ISAP,只需要一次BFS的東西……
可惡,竟然沒有找到不用gap優化的寫法 T^T
ISAP演演算法從某種程度上是SAP演演算法和Dinic的融合
SAP演演算法就是所謂的EK演演算法……ISAP也就是Improved SAP……但是主體怎麼跟DInic幾乎一模一樣!
演演算法流程如下:
-
從 \(T\) 開始進行BFS,直到 \(S\) ,標記深度,同時記錄當前深度有多少個
-
利用DFS不斷尋找增廣路,思路與Dinic類似
-
每次回溯結束後,將所在節點深度加一(遠離 \(T\) 一點),同時更新深度記錄。如果出現了斷層(有一個深度沒有點了)那麼結束尋找。
?: 為什麼需要深度加一
由於我們在便利過一次過後,這個點不可能再向更靠近 \(T\) 的點送出流量,所以只能退而求其次,給自己同層的結點送流量。
怎麼跟Dinic一摸一樣啊,關鍵是也可以用當前弧優化,只是我用寫的是vetor存圖……用不了
參考程式碼……
提交題目還是【模板】網路最大流 - 洛谷
!! 竟然在最優解第二頁 O-O
對於下面程式碼做出一些解釋
?: 為什麼終止條件是
dep[s] > n考慮如果是
dep[s] <= n的情況,由於只有n個點,意味著只要最大深度 \(\lt n\) 那麼要麼是有連續的層,要麼斷層了(此時我們在DFS中會將dep[s]設為n+1如果最大深度 \(\gt n\) 所以一定會有一個深度是沒有點的,意味著一定出現了斷層,也就是流量無法到達了
所以,更新答案之後就可以結束迴圈了
// 寫這個的時候,借鑑了寫HLPP最優解的大佬寫快讀的方法……
template<typename T>
inline void read(T &x) {
char c, f(0); x = 0;
do if ((c = getchar()) == '-') f = true; while (isspace(c));
do x = (x<<3) + (x<<1) + (c ^ 48), c = getchar(); while (isdigit(c));
if (f) x = -x;
}
template <typename T, typename ...Args> inline void read(T &t, Args&... args) { read(t), read(args...); }
typedef long long Data;
using namespace std;
const int N = 207, M = 5007;
struct Edge {
int to;
size_t rev; // 反邊的位置,用int也沒問題
Data flow;
Edge(int to, size_t rev, Data f) : to(to), rev(rev), flow(f) {}
};
class ISAP {
public:
int n, m, s, t;
vector<int> dep;
int q[N * 2], gap[N * 2];
// vector< vector<Edge> > v;
vector<Edge> v[N * 2];
ISAP(int n, int m, int s, int t) : n(n), m(m), s(s), t(t) {
input();
}
inline void input() {
// v.resize(n + 1);
for (int x, y, f, i(0); i ^ m; ++i) {
read(x, y, f);
v[x].push_back(Edge(y, v[y].size(), f));
v[y].push_back(Edge(x, v[x].size() - 1, 0));
}
}
inline void init() {
dep.assign(n + 1, -1);
dep[t] = 0, gap[0] = 1;
// 如果要用手寫佇列,要開大一點……避免玄學RE,雖然理論上N就夠了
register int qt(0), qf(0);
q[qt++] = t;
int x, y;
while (qf ^ qt) {
x = q[qf++];
for (auto &e : v[x]) {
if (dep[(y = e.to)] == -1) // if dep[y] != -1
++gap[(dep[y] = dep[x] + 1)], q[qt++] = y;
}
} // bfs end
}
inline Data sap(int x, Data flow) {
if (x == t) return flow;
Data rest = flow;
int y, f;
for (auto &e : v[x]) {
if (dep[(y = e.to)] + 1 == dep[x] && e.flow) {
f = sap(y, min(e.flow, rest));
if (f) {
e.flow -= f, v[e.to][e.rev].flow += f;
rest -= f;
}
if (!rest) return flow; // flow all used
}
}
// change dep
if (--gap[dep[x]] == 0) dep[s] = n + 1; // can not reach to t
++gap[++dep[x]]; // ++depth
return flow - rest;
}
inline Data calc() {
Data maxflow(0);
static const Data INF(numeric_limits<Data>::max());
// dep[s]最大為n,為一條鏈的時候
while (dep[s] <= n) {
// 如果要當前弧優化,在這裡需要重置當前弧的now!
maxflow += sap(s, INF);
}
return maxflow;
}
};
int main() {
int n, m, s, t;
read(n, m, s, t);
static ISAP isap(n, m, s, t);
isap.init();
printf("%lld\n", isap.calc());
return 0;
}
?: 如果我想用vector存圖實現當前弧優化怎麼整
在sap函數的主體部分
for (int & i = now[x]; i < G[x].size(); ++i) {
Edge & e = G[x][i];
if (dep[(y = e.to)] + 1 == dep[x] && e.flow) {
f = sap(y, min(rest, e.flow));
if (f) {
rest -= f, e.flow -= f;
G[e.to][e.rev].flow += f;
}
if (!rest) return flow;
}
}
在calc不部分
while (dep[s] <= n) {
now.assign(n, 0);
maxflow += sap(s, INF);
}
然後……就搞定了QwQ
作者有話說
一般來說,如果圖非常稠密(邊數遠遠大於點數),當前弧優化的力度就非常大了
如:Zoj3229 Shoot the Bullet|東方文花帖|【模板】有源匯上下界最大流 - 洛谷
這個專題我會放在網路流的其他部分詳解,敬請期待……
寫了當前弧優化的Dinic能輕鬆過……沒寫全TLE
雖然沒寫當前弧優化的ISAP能更快的過前三個點,但最後一個點過不了……QwQ
我沒有試過當前弧優化的ISAP更新:有當前弧優化的ISAP可以過
但是如果邊數不多,當前弧優化可能就成了負優化了……所以需要根據題目資料合理使用