\(\newcommand\m\mathbf\) \(\newcommand\t\texttt\)

\(\text{By DaiRuiChen007}\)

約定：

• 對於兩個字串 \(S,T\)，用 \(ST\) 表示將 \(T\) 接在 \(S\) 後面得到的字串（即 \(S+T\)）
• 對於兩個字串 \(S,T\)，若 \(S\) 的字典序嚴格小於 \(T\) 的字典序則即 \(S<T\)，若在滿足 \(S<T\) 的前提下滿足 \(S\) 不是 \(T\) 的字首，我們記 \(S\ll T\)，同理能夠得到 \(S>T\) 和 \(S\gg T\) 的定義

一、Lydon Word

I. Lyndon Word 的定義

假如某個字串 \(S\) 滿足 \(|root(S)|=|S|\)，且 \(S\) 嚴格小於 \(S\) 的所有迴圈同構串，那麼稱 \(S\) 是一個 Lyndon Word，簡記為 LW，並假設所有 LW 構成的集合為 \(\m{LW}\)

II. Lyndon Word 的性質

Lyndon Word 與 Border

斷言：對於所有 \(w\in\m{LW}\)，均滿足：\(w\) 沒有 Border，證明如下：

證：

採用反證法，設某個 LW \(w\) 中有 Border \(u\)

不妨設 \(w=ux=yu\)，那麼由於 LW 的性質，\(xu>w,uy>w\)

又因 \(w=yu\)，所以 \(xu>yu\)，所以 \(x>y\)，同理根據 \(uy>ux\) 有 \(y>x\)

顯然匯出矛盾，故原命題成立

Lyndon Word 與字尾

Lyndon Word 有等價定義：\(w\in\m{LW}\) 當且僅當 \(w\) 小於其所有真字尾，證明如下：

證：

假設 \(v\) 為 \(w\) 的任意真字尾，且 \(w=uv\)

• 證明 \(w<v\implies w<vu\)

  由於 \(|w|>|v|\)，因此 \(w\ll v\)，此時 \(w\ll vu\)，故原命題得證

• 證明 \(w<vu\implies w<v\)

  考慮 \(w'=w[1\cdots |v|]\)，顯然 \(w'\le w\)，若 \(w'=w\) 那麼 \(v\) 是 \(w\) 的一個 Border，與上一個性質矛盾，因此我們知道 \(w'<v\)，又因為 \(|w'|=|v|\) 且 \(w'\ne v\)，所以 \(w'\ll v\) 所以 \(w<v\)

綜上所述，我們證明了 \(w<v\iff w<vu\)，那麼我們就證明了原命題等價於 LW 的定義，因此「\(w\) 小於其所有真字尾」也是 LW 一個等價的定義

Lyndon Word 的標準分解

Lyndon Word 的複合

假設 \(u,v\in\m{LW}\)，那麼 \(uv\in\m{LW}\iff u<v\)，證明如下：

證：

• 證明 \(uv\in\m{LW}\implies u<v\)

  根據 LW 的等價定義，\(uv\ll v\)，又因為 \(u<uv\)，因此 \(u<v\) 得證

• 證明 \(u<v\implies uv\in\m{LW}\)

  考慮 \(uv\) 的任意一個真字尾 \(s\)

  • \(|s|>|v|\) 時

    假設 \(s=u'v\)，注意到 \(u'\) 是 \(u\) 的真字尾，那麼我們知道 \(u'\gg u\)，所以我們知道 \(u'\gg uv\) 則 \(s\gg uv\)

  • \(|s|<|v|\) 時

    此時 \(s\) 為 \(v\) 的真字尾，那麼 \(s\gg v\)，且 \(v>u\)，故 \(s\gg u\) 所以 \(s>uv\)

  • \(|s|=|v|\) 時

    顯然有 \(s=v\)，即證 \(v>uv\)

    • 若 \(u\ll v\)

      此時顯然有 \(uv\ll v\)

    • 若 \(u\) 為 \(v\) 的字首

      記 \(v=uv'\)，即證 \(uv'>uv\)，事實上我們只需要比較 \(v'\) 和 \(v\) 的大小即可，注意到 \(v'\) 為 \(v\) 的一個真字尾且 \(v\) 為 LW，那麼 \(v'>v\) 成立，所以 \(v>uv\) 成立

  綜上所述，\(u<v\implies uv\in\m{LW}\)

所以我們證明了 \(\forall u,v\in \m{LW}\)，\(uv\in\m{LW}\iff u<v\)

Lyndon Word 的分解

假設 \(w\in\m{LW}\) 且 \(|w|\ge 2\)，設 \(v\) 為 \(w\) 的最小真字尾，記 \(w=uv\)，則 \(u,v\) 滿足 \(u<v\) 且 \(u,v\in\m{LW}\)，證明如下：

證：

• 證明 \(v\in\m{LW}\)

  事實上，考慮 \(v\) 的每個真字尾 \(v'\)，由於 \(v'\) 也是 \(w\) 的一個真字尾，那麼 \(v< v'\) 同樣成立，因此 \(v\in\m{LW}\)

• 證明 \(u<v\)

  • 若 \(|u|\ge |v|\)

    那麼 \(w<v\) 等價於 \(u<v\)，此時命題成立

  • 若 \(|u|<|v|\)

    此時由於 \(w<v\) 那麼 \(u\le v[1\cdots |u|]\)

    • 若 \(u< v[1\cdots|u|]\)

      由於 \(|u|=|v|\) 且 \(u\ne v\)，那麼 \(u\ll v[1\cdots |u|]\) 則 \(u<v\)

    • 若 \(u=v[1\cdots |u|]\)

      此時 \(u\) 是 \(v\) 字首同樣有 \(u<v\) 成立

• 證明 \(u\in \m{LW}\)

  考慮反證法，存在一個 \(u\) 的真字尾 \(u'<u\)，那麼考慮 \(w\) 的真字尾 \(u'v\)

  • 若 \(u'\ll u\)

    那麼一定有 \(u'v<uv=w\) 與 \(w\) 是 LW 矛盾

  • 若 \(u'\) 為 \(u\) 字首

    此時設 \(u=u't\)，由於 \(w\) 是 LW，那麼應該滿足 \(u'v>uv\)，那麼 \(u'v>u'tv\) 即 \(v>tv\)，此時出現了一個比 \(v\) 更小的 \(w\) 的真字尾，這與假設矛盾

  綜上，\(u\) 必須是 LW

綜上所述，此時有 \(u<v\) 且 \(u,v\in\m{LW}\)

此時我們可以證明 \(v\) 是 \(w\) 最大的一個 LW 真字尾，證明如下：

證：

假設存在另一個 \(w\) 的 LW 真字尾 \(v'\) 滿足 \(|v'|>v\)，那麼 \(v\) 是 \(v'\) 的真字尾，由於 \(v'\in\m{LW}\)，那麼 \(v>v'\) 這與 \(v\) 是 \(w\) 的最小真字尾矛盾

而此時我們記 \(w=uv\) 為 \(w\) 的標準分解

基於標準分解的 Lyndon Word 定義形式

\(w\in\m{LW}\) 等價於 \(|w|=1\) 或 \(|w|\ge 2\) 且存在 \(u,v\in\m{LW}\) 滿足 \(u<v\) 且 \(w=uv\)

證明如下：

證：

當 \(|w|=1\) 時原命題顯然成立，因此只討論 \(|w|\ge 2\) 的情況，簡記該判定條件為「\(\exists u,v\)」

• 證明 \(\exists u,v\implies w\in\m{LW}\)

  根據「Lyndon Word 的複合」一節中的結論，我們知道這個結論是成立的

• 證明 \(w\in\m{LW}\implies \exists u,v\)

  設 \(v\) 為 \(w\) 的最小真字尾，且 \(u\) 滿足 \(w=uv\)，根據「Lyndon Word的分解」一節中的結論，我們知道此時的 \(uv\) 就滿足條件

綜上所述，我們知道 \(|w|=1\text{ or }\exists u,v\) 也是一個 LW 的判定方式

III. Lyndon Word 的經典問題

Lyndon Word 的後繼問題

假設字元集為 \(\{1,2,\cdots,\sigma\}\)，且字串長度 \(\le n\)，給定滿足條件的 LW \(S\)，求字典序大於 \(S\) 的最小合法 LW \(S'\)

給出一個構造方法，先將 \(S\) 不斷迴圈拼接得到一個長度為 \(n\) 的字串 \(S^\star\)（最後一個週期可以不是整週期），找到 \(S^\star\) 最後一個不是 \(\sigma\) 的字元 \(S^\star_k\)，並讓 \(S^\star_k\gets S^\star_k+1\)，然後刪掉子串 \(S^\star[k+1\cdots n]\) 就得到了 \(S\) 的後繼 \(S'\)，證明如下：

證：

• 證明 \(S'\in\m{LW}\)

  注意到 \(S^\star[1\cdots k]\) 一定是一個近似 LW，而讓 \(S^\star_k\gets S^\star_k+1\)，我們就得到了一個 LW，有關「近似 LW」的內容以及相關證明請參看後文「Duval 演演算法求 Lyndon 分解」一章中的「引理」部分和「演演算法流程」部分的第二種情況，會給出一個嚴謹的證明

• 證明不存在 \(T\in\m{LW}\) 滿足 \(S<T<S'\)

  根據定義，比較 \(T,S'\)，假設 \(i\) 表示滿足 \(T_i<S'_i\) 的最小 \(i\)，顯然 \(T[1\cdots |S|]=S\) 所以 \(i\ge |S|\)

  假設 \(k\times|S|<i\le (k+1)\times |S|\)，且 \(i-k\times|S|=r\in[1,|S|]\)

  • 若 \(i<|S'|\)

    考慮 \(T\) 的真字尾 \(T[k\times |S|+1\cdots |T|]\)

    根據假設，\(S’[k\times|S|+1\cdots i-1]=T[k\times |S|+1\cdots i-1]\)

    由於 \(S'\) 的構造定理，\(S'[k\times |S|+1\cdots i-1]=S[1\cdots r-1]=T[1\cdots r-1]\)

    因此，我們如果要比較 \(T\) 與 \(T[k\times |S|+1\cdots |T|]\) 的大小關係，只需比較 \(T_i\) 與 \(T_{r}\) 的大小

    注意到 \(T_i<S'_i=S_r<T_r\)，因此 \(T[k\times |S|+1\cdots |T|]<T\)

    與 \(T\in\m{LW}\) 矛盾，故這種情況不存在

  • 若 \(i=|S'|\)

    根據對 \(S'\) 的定義，我們知道 \(k\times |S|<|S'|\le (k+1)\times |S|\)，所以 \(|T|\le (k+1)\times S\)

    根據定義，此時必然有 \(T_i=S'_i-1=S_{r}\)，同樣考慮 \(T\) 的真字尾 \(T[k\times |S|+1\cdots |T|]\)

    注意到 \(T[i+1\cdots |T|]\le \sigma^{|T|-i}\) 且 \(T[r+1\cdots |S|]=S[r+1\cdots |S|]=\sigma^{|S|-r}\)，因此 \(T[i+1\cdots |T|]\le S[r+1\cdots |S|]\)

    又因為 \(T[k\times |S|+1\cdots |T|]>T\)，這就要求 \(T[k\times|S|+1\cdots i]\gg T[1\cdots r]\)，又因為事實上 \(T[k\times |S|+1\cdots i]=T[1\cdots r]\)，這就匯出了矛盾

綜上，我們證明了 \(S'\) 是 \(S\) 在 \(\m{LW}\) 中的後繼

Lyndon Word 的計數問題

設字串長度恰好為 \(n\)，字元集大小為 \(m\)，統計所有這樣的字串中 LW 的數量

首先考慮 \(S\in\m{LW}\) 的判定條件：

• \(|root(S)|=|S|\)
• \(S\) 小於 \(S\) 的所有迴圈同構串

先考慮第二個問題，假如我們不保證 \(|root(S)|=|S|\)，那麼我們可以考慮對「\(S\) 小於等於 \(S\) 的所有迴圈同構串」的 \(S\) 進行計數，然後再在這些串中統計 \(|root(S)|=|S|\) 的即可

為了解決第一個問題，我們可以這樣想：把每個 \(S\) 都到環上，即變成圓排列的形式，那麼一個圓排列中的滿足條件的 \(S\) 有且僅有一個，所以我們只需要求長度為 \(n\)，值域為 \(m\) 的有旋轉無翻轉圓排列計數即可，記這個問題的答案為 \(S_n\)

接下來考慮第二個問題：在 \(S_n\) 個圓排列中，只有那些最小整週期為 \(n\) 的才能轉化成一個 LW，因此我們記：在 \(S_n\) 個圓排列中，最小整週期恰好為 \(n\) 的圓排列的個數為 \(T_n\)

容易證明 \(T_n\) 就是我們要求的答案

首先考慮如何根據 \(T_n\) 推匯出 \(S_n\)，顯然對於一個最小整週期為 \(d\) 且 \(d\mid n\) 的長度為 \(d\) 的圓排列 \(T\)，我們構造 \(S=\underbrace{TT\cdots T}_{n/d\text{ times}}=T^{n/d}\)，顯然這樣的 \(S\) 與 \(T\) 之間存在雙射，即我們可以證明對於 \(T\) 進行旋轉後得到 \(T'\)，則 \(S'=(T')^{n/d}\) 與 \(S\) 是迴圈同構的

因此我們知道對於所有長度為 \(n\)，最小整週期為 \(d\) 的圓排列，其總數恰好為 \(T_d\)，因此我們得到如下的公式：

注意到這個式子實際上等價於 \(S=T*1\)，其中 \(S(n)=S_n,T(n)=T_n,1(n)=1\)，\(*\) 為狄利克雷折積符號

那麼根據莫比烏斯反演，我們能夠得到 \(T=S*\mu\)，即：

因此問題轉化為求 \(S_d\) 的值，而求 \(S\) 事實上是一個經典的項鍊計數問題，在《具體數學》第四章有如下的解法：

解：

對於 \(S_n\) 個本質不同圓排列，我們任意寫出其對應的一個字串，對於每個字串，再寫出其 \(n\) 個迴圈同構串，構成一個可重集 \(\m A\)，顯然 \(|\m A|=n\times S_n\)，對 \(|\m A|\) 進行 Double-Couting，考慮每個字串 \(S=S_1S_2S_3\cdots S_{n}\) 出現的次數，根據迴圈同構的定義得到：

\[|\m A|=\sum_S\sum_{i=1}^{n}[S_1S_2\cdots S_{n}=S_iS_{i+1}\cdots S_{n}S_1\cdots S_{i-1}] \]

交換求和號，轉化為統計貢獻的形式：

\[|\m A|=\sum_{i=1}^{n}\sum_S[S_1S_2\cdots S_{n}=S_iS_{i+1}\cdots S_{n}S_1\cdots S_{i-1}] \]

注意到對於給定的 \(i\)，滿足條件的 \(S\) 當且僅當 \(S\) 有一個大小為 \(i\) 的約數的整週期，事實上，根據整週期的性質，這等價於 \(S\) 有整週期 \(\gcd(n,i)\)

根據整週期的性質，有整週期 \(\gcd(n,i)\) 的 \(S\) 的數量等價於長度為 \(\gcd(n,i)\) 的任意字串的數量，即 \(m^{\gcd(n,i)}\) 種

所以可以優化掉第二個求和號，再根據 \(\gcd(n,i)\) 的性質對於不同的 \(d=\gcd(n,i)\) 統計對應 \(i\) 的數量，不難得到如下變形過程：

\[|\m A|=\sum_{i=1}^{n} m^{\gcd(n,i)}=\sum_{d\mid n}\varphi\left(\dfrac nd\right)\times m^d \]

運用 \(|\m A|=n\times S_n\) 的事實得到 \(S_n=\dfrac 1n\sum_{d|n}\varphi\left(\tfrac nd\right)\times m^d\)

所以我們得到了 \(S_n\) 的一個簡潔表達，據此計算 \(T_n\) 即可，不過事實上，\(T_n\) 也有更加優美的形式，具體分析如下：

解：

記 \(id(n)=n\)，根據狄利克雷折積和莫比烏斯反演的基本推論有 \(id=\varphi*1\implies \varphi=id*\mu\)

注意到 \(S=T*1\)，且 \(nS=n(T*1)\)，我們記一個新的函數 \(T'(n)=nT_n\)，注意這裡的兩個 \(n\) 都是自變數而非常數，考慮建構函式 \(id*T'\)，根據狄利克雷折積定義進行展開：

\[\begin{aligned} id*T'(n) &=\sum_{d\mid n}id\left(\dfrac nd\right)\times T'(d)\\ &=\sum_{d\mid n}\dfrac nd\times(d\times T_n)\\ &=n\sum_{d\mid n} T_n\\ &=n\times(T*1(n)) \end{aligned} \]

因此 \(id*T'=n(T*1)\)，故 \(n\times S_n=id*T'\)

此時結合 \(nS=\varphi* m^n(n)\) 運用莫比烏斯反演得到：\(id*T'=nS=\varphi *m^n(n)=id*\mu*m^n(n)\)

因此 \(T'=\mu*m^n(n)\)

綜上所述，我們得到 \(T_n=\dfrac 1n\sum_{d\mid n}\mu\left(\dfrac nd\right)\times m^d\)

IV. 習題演練

[CSES2209] - Counting Necklaces

Problem Link

項鍊計數模板，求 \(S_n\) 的值即可，可以用線性篩預處理 \(\varphi(n)\) 的值

時間複雜度 \(\Theta(n+\sqrt n\log n)\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e6+1,MOD=1e9+7;
int n,m,phi[MAXN];
bool mark[MAXN];
vector <int> primes;
inline int ksm(int a,int b,int m=MOD) {
	int ret=1;
	while(b) {
		if(b&1) ret=a*ret%MOD;
		a=a*a%MOD;
		b=b>>1;
	}
	return ret;
}
inline int calc(int d) {
	return ksm(m,d)*phi[n/d]%MOD;
}
signed main() {
	int ans=0;
	scanf("%lld%lld",&n,&m);
	phi[1]=1;
	for(int i=2;i<=n;++i) {
		if(!mark[i]) phi[i]=i-1,primes.push_back(i);
		for(int p:primes) {
			if(p*i>n) break;
			mark[p*i]=true,phi[p*i]=(i%p==0)?(phi[i]*p):(phi[i]*(p-1));
			if(i%p==0) break;
		}
	}
	for(int i=1;i*i<=n;++i) {
		if(n%i!=0) continue;
		ans=(ans+calc(i))%MOD;
		if(i*i!=n) ans=(ans+calc(n/i))%MOD;
	}
	printf("%lld\n",ans*ksm(n,MOD-2)%MOD);
	return 0;
}

[CSES2210] - Counting Grids

Problem Link

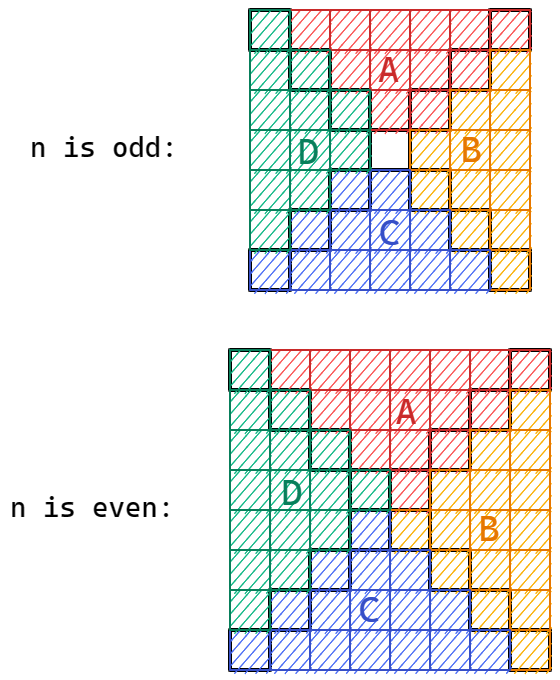
類似上一個問題，記答案為 \(S_n\)，對於一個染色的 \(n\times n\) 網格，將其旋轉四次後做 Double-Counting，考慮每個網格在旋轉多少度後重復出現了多少次

如上圖，根據旋轉網格的性質我們可以把一個網格劃分成 \(4\) 塊，分別是 \(A,B,C,D\)，不難發現每次旋轉後只會交換 \(A,B,C,D\) 的相對順序，並不會改變 \(A,B,C,D\) 的塊內心態，記每塊的大小為 \(m\)，對 \(n\) 的奇偶性分別討論：

• \(n\) 為奇數時

  此時 \(m=\dfrac{n^2-1}4\)

  • 某個網格在旋轉 \(0^\circ\) 時出現過

    任何的網格都符合這樣的要求，這樣的網格共有 \(2^{n\times n}\) 個

  • 某個網格在旋轉 \(180^\circ\) 時出現過

    這要求 \(A=B,C=D\)，而中間的那個位置可以隨便取色，這樣的網格共有 \(2\times 2^m\times 2^m=2^{2\times m+1}\)

  • 某個網格在旋轉 \(90^\circ\) 或 \(270^\circ\) 時出現過

    這要求 \(A=B=C=D\)，而中間那個位置依然可以隨便取色，這樣的網格共有 \(2\times 2^m=2^{m+1}\) 個

  綜上，我們得到 \(4\times S_n=2^{n\times n}+2^{m+1}+2^{2\times m+1}+2^{m+1}\)，當 \(n>1\) 時，\(S_n=2^{n\times n-2}+2^{2\times m-1}+2^m\)，當 \(n=1\) 時 \(S_n=2\)

• \(n\) 為偶數時

  此時 \(m=\dfrac{n^2}4\)

  • 某個網格在旋轉 \(0^\circ\) 時出現過

    任何的網格都符合這樣的要求，這樣的網格共有 \(2^{n\times n}\) 個

  • 某個網格在旋轉 \(180^\circ\) 時出現過

    這要求 \(A=B,C=D\)，這樣的網格共有 \(2^m\times 2^m=2^{2\times m}\)

  • 某個網格在旋轉 \(90^\circ\) 或 \(270^\circ\) 時出現過

    這要求 \(A=B=C=D\)，而中間那個位置依然可以隨便取色，這樣的網格共有 \(2^m\) 個

  綜上，我們得到 \(4\times S_n=2^{n\times n}+2^{m}+2^{2\times m}+2^m\)，則 \(S_n=2^{n\times n-2}+2^{2\times m-2}+2^{m-1}\)

綜上所述，我們得到 \(S_n\) 的表示式：

快速冪計算即可

時間複雜度 \(\Theta(\log n)\)

#include<bits/stdc++.h> 
#define int long long
using namespace std;
const int MOD=1e9+7;
inline int ksm(int a,int b,int m=MOD) {
	int ret=1;
	while(b) {
		if(b&1) ret=a*ret%MOD;
		a=a*a%MOD;
		b=b>>1;
	}
	return ret;
}
signed main() {
	int n;
	scanf("%lld",&n);
	int m=(n%2==1)?((n*n-1)/4):(n*n/4);
	if(n==1) puts("2");
	else if(n%2==1) printf("%lld\n",(ksm(2,n*n-2)+ksm(2,2*m-1)+ksm(2,m))%MOD);
	else printf("%lld\n",(ksm(2,n*n-2)+ksm(2,2*m-2)+ksm(2,m-1))%MOD);
	return 0;
}

[BZOJ1361] - [WC2004]孿生項鍊

Problem Link

根據「Lyndon Word」的經典問題一節中介紹的公式計算即可，注意第一問要寫高精度

時間複雜度 \(\Theta(k\sqrt k+n)\)，其中 \(\Theta(k\sqrt k)\) 的 \(\Theta(\sqrt k)\) 是列舉因子數量 \(\Theta(k)\) 是高精度複雜度

#include<bits/stdc++.h> 
using namespace std;
const int MAXN=1001;
struct BigInt {
	vector <int> dig;
	BigInt() { dig.clear(); }
	BigInt(vector <int> _dig) { dig=_dig; }
	BigInt(int x) {
		while(x) dig.push_back(x%10),x/=10;
	}
	inline int& operator [](int x) { return dig[x]; }
	inline int length() { return (int)dig.size(); }
	inline void update() {
		while(!dig.empty()&&dig.back()==0) dig.pop_back();
	}
	inline friend BigInt operator +(BigInt &A,BigInt &B) {
		BigInt C(vector<int>(max(A.length(),B.length())+1,0));
		for(int i=0;i<A.length();++i) C[i]+=A[i];
		for(int i=0;i<B.length();++i) C[i]+=B[i];
		for(int i=0;i<C.length()-1;++i) C[i+1]+=C[i]/10,C[i]%=10;
		C.update();
		return C;
	}
	inline friend BigInt operator -(BigInt &A,BigInt &B) {
		BigInt C(vector<int>(max(A.length(),B.length())+1,0));
		for(int i=0;i<A.length();++i) C[i]+=A[i];
		for(int i=0;i<B.length();++i) C[i]-=B[i];
		for(int i=0;i<C.length()-1;++i) while(C[i]<0) --C[i+1],C[i]+=10;
		C.update();
		return C;
	}
	inline friend BigInt operator /(BigInt &A,const int &d) {
		BigInt B(vector<int>(A.length(),0));
		for(int i=A.length()-1,r=0;i>=0;--i) r=r*10+A[i],B[i]=r/d,r%=d;
		B.update();
		return B;
	}
	inline void print() {
		for(int i=(int)dig.size()-1;i>=0;--i) printf("%d",dig[i]);
		puts("");
	}
}	pw[MAXN];
int mu[MAXN];
bool mark[MAXN];
vector <int> primes;
signed main() {
	int n,m,k;
	string S;
	cin>>n>>m>>k>>S;
	//task 1
	pw[0]=BigInt(1);
	for(int i=1;i<=k;++i) mu[i]=1,pw[i]=pw[i-1]+pw[i-1];
	for(int i=2;i<=k;++i) {
		if(!mark[i]) mu[i]=-1,primes.push_back(i);
		for(int p:primes) {
			if(p*i>k) break;
			mark[p*i]=true,mu[p*i]=(i%p==0)?0:(-mu[i]);
			if(i%p==0) break;
		}
	}
	BigInt ans(0);
	for(int i=1;i*i<=k;++i) {
		if(k%i!=0) continue;
		if(mu[i]==1) ans=ans+pw[k/i];
		if(i*i!=k&&mu[k/i]==1) ans=ans+pw[i];
	}
	for(int i=1;i*i<=k;++i) {
		if(k%i!=0) continue;
		if(mu[i]==-1) ans=ans-pw[k/i];
		if(i*i!=k&&mu[k/i]==-1) ans=ans-pw[i];
	}
	ans=ans/k;
	ans.print();
	//task 2
	string T;
	while((int)T.length()<n) T=T+S;
	T.resize(n);
	while(!T.empty()&&T.back()=='1') T.pop_back();
	assert(!T.empty());
	T[(int)T.length()-1]='1';
	cout<<T<<"\n";
	return 0;
}

[CodeForcesGym - 100162G] - Lyndon Words

從 \(\texttt{a}\) 開始每次暴力找字尾就行，注意實現常數，比如不要用 STL string 類，最好自己手寫一個字元陣列維護一下尾指標就行

#include<bits/stdc++.h> 
using namespace std;
const int MAXN=31;
char ch[MAXN];
signed main() {
	int n,m,l,r,T=0;
	while(scanf("%d%d%d%d",&n,&m,&l,&r)!=EOF) {
		char sigma=m-1+'a';
		printf("Case %d:\n",++T);
		int tail=0; ch[++tail]='a';
		for(int id=1;id<=r;++id) {
			if(l<=id) {
				for(int i=1;i<=tail;++i) putchar(ch[i]);
				putchar('\n');
			}
			int cyc=tail;
			while(tail<n) {
				++tail;
				ch[tail]=ch[tail-cyc];
			}
			while(ch[tail]==sigma) --tail;
			++ch[tail];
		}
	}
}

二、Lyndon 分解

I. Lyndon 分解定理

Lyndon 分解的定義

首先定義對於任意字串 \(S\) 的一個 Lyndon 分解：

Lyndon 分解指的是一個字串序列 \(w=\{w_1,w_2,w_3,\cdots,w_k\}\)，滿足 \(S=w_1w_2w_3\cdots w_k\)，其中 \(w_i\in\m{LW}\)，且 \(w_1\ge w_2\ge w_3\ge\cdots\ge w_k\)

Lyndon 分解定理

Lyndon 分解定理告訴我們，對於任意字串 \(S\)，其 Lyndon 分解存在且唯一

Lyndon 分解的存在性

首先我們把 \(S\) 寫成 \(S=S_1S_2S_3\cdots S_{|S|}\)，此時我們就把 \(S\) 寫成了 \(|S|\) 個 LW 的形式

此時對於任意兩個相鄰的 LW \(w_i,w_{i+1}\)，若 \(w_i<w_{i+1}\) 我們就把 \(w_i,w_i+1\) 合併成 \(w_iw_{i+1}\) 不斷重複這個過程直到這樣的 \(w_i,w_{i+1}\) 不存在為止，可以證明這個過程一定會停止，那麼我們就得到了一個 Lyndon 分解

Lyndon 分解的唯一性

假設 \(S\) 存在兩個不同的 Lyndon 分解 \(w_1\sim w_k\) 與 \(w'_1\sim w'_{k'}\)

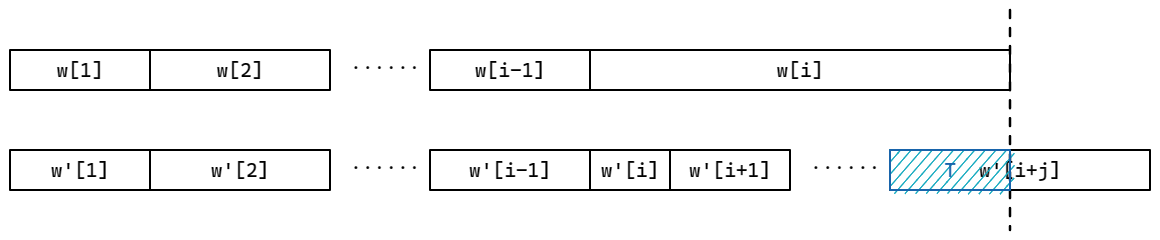
如下圖，假設 \(w_i\) 與 \(w'_i\) 是這兩個分解第一個不同的地方，且 \(|w_i|>|w'_i|\)，我們設 \(|w'_iw'_{i+1}\cdots w'_{i+j}|\ge w_i\)，且 \(|w'_iw'_{i+1}\cdots w'_{i+j-1}|< w_i\)，顯然 \(j\ge 1\)，\(T\) 為 \(w_i\) 與 \(w'_{i+j}\) 的交

根據 \(w'\) 是一個 Lyndon 分解的假設，我們得到 \(T\le w'_{i+j}\le w'_{i+j-1}\le\cdots\le w'_i\le w_i\)，又因為 \(T\) 是 \(w_i\) 的一個真字尾，那麼 \(T\le w_i\) 與 \(w_i\) 是 LW 的要求矛盾，因此這樣的 Lyndon 分解必須是唯一的

II. Lyndon 分解的性質

定義 \(w=\{w_1,w_2\cdots ,w_k\}\) 為 \(S\) 的 Lyndon 分解，我們有如下的性質：

Lyndon 分解與最小字尾

\(w_k\) 為 \(S\) 的最小字尾，證明如下：

證：

對於長度小於 \(|w_k|\) 的字尾，根據 \(w_k\) 是 LW 的事實即可得到所有長度小於 \(|w_k|\) 的字尾字典序一定大於 \(w_k\)

而對於任意長度大於 \(|w_k|\) 的字尾 \(S'\)，我們設 \(S'=w'_iw_{i+1}w_{i+2}\cdots w_k\)，其中 \(w'_i\) 是 \(w_i\) 的一個字尾，那麼根據 Lyndon 分解的定義，\(w_k\le w_{k-1}\le\cdots \le w_i\)，且由於 \(w'_i\) 是 LW \(w_i\) 的一個字尾，我們知道 \(w'_i\le w_i\)，因此 \(w_k\le w'_i\) 又因 \(|S'|>|w_k|\)，所以 \(S'>w_k\)

綜上，\(w_k\) 為 \(S\) 的最小字尾

Lyndon 分解與最長 LW 字尾

\(w_k\) 為 \(S\) 最大的 LW 字尾，證明如下：

證：

對於任意長度大於 \(|w_k|\) 的字尾 \(S'\)，我們設 \(S'=w'_iw_{i+1}w_{i+2}\cdots w_k\)，其中 \(w'_i\) 是 \(w_i\) 的一個字尾，同上面的分析，\(S'>w_k\)，那麼 \(S'\) 必然不可能是 LW

Lyndon 分解與最長 LW 字首

\(w_1\) 為 \(S\) 最大的 LW 字首，證明如下：

證：

對於任意長度大於 \(|w_1|\) 的字首 \(S'\)，我們設 \(S'=w_1w_2\cdots w'_i\)，其中 \(w'_i\) 為 \(w_i\) 的一個字首，類似上面的過程，我們得到 \(w'_i\le w_i\le w_{i-1}\le\cdots \le w_1\)，且 \(|w'_i|<|S'|\)，因此 \(w'_i<S'\)，那麼 \(S'\) 必然不可能是 LW

III. Duval 演演算法求 Lyndon 分解

介紹

Duval 演演算法是一種支援在 \(\Theta(|S|)\) 時間內求出 \(S\) 的 Lyndon 分解的演演算法

引理

我們定義字串 \(w'\) 為「近似LW」當且僅當存在 \(w\in\m{LW}\) 使得 \(w'\) 為 \(w\) 的一個字首

那麼我們有如下的引理：若 \(w’\) 為一個近似 LW，其中 \(\t c\) 為 \(w'\) 的最後一個字元，如果把 \(\t c\) 修改成一個更大的字元 \(\t d\) ，那麼新的 \(w'\) 為一個 LW

證：

不妨設 \(w'u\) 為一個 LW，那麼考慮 \(w'\) 的一個真字尾 \(v\)，記 \(w=v'v\)，那麼根據 \(w'u\) 為 LW，我們知道 \(vu>w'u\)，且 \(|v|<|w'|\)，考慮 \(v\) 和 \(w'[1\cdots |v|]\) 的大小關係，顯然 \(v\ge w'[1\cdots |v|]\)

那麼此時考慮增大 \(w'\) 的末尾，那麼 \(v\) 的末尾會增大且 \(w'[1\cdots |v|]\) 的末尾不會增大，因此 \(v> w'[1\cdots|v|]\)，由於 \(v\ne w'[1\cdots |v|]\)，所以 \(v\gg w'[1\cdots |v|]\) 所以 \(v>w'\)，故修改後的 \(w'\) 是一個 LW

維護內容

如下圖，在 Duval 演演算法的過程中，我們將整個字串 \(S\) 分成了三個部分，並且維護了一些變數：

• \(S_1\)：已經掃描並處理完成的串
• \(w_1\sim w_g\)：一些滿足 \(w_1\ge w_2\ge \cdots\ge w_g\) 且 \(S_1=w_1w_2\cdots w_g\) 的一些 LW
• \(i\)：\(S_1\) 的尾指標，滿足 \(S_1=S[1\cdots i-1]\)，\(S_2\) 的頭指標
• \(S_2\)：已經掃描但尚未處理完成的串
• \(t_1\sim t_h\)：一些滿足 \(t_1=t_2=\cdots =t_h\) 的 LW，且 \(w_g>t_h\)
• \(t'\)：\(S_2\) 拆分後剩下的一個近似 LW 串，滿足 \(t'\) 是 \(t_h\) 的某個字首
• \(j\)：維護 \(t'\) 與 \(t_h\) 的匹配長度
• \(k\)：\(S_2\) 的尾指標，滿足 \(S_2=S[i\cdots k-1]\)，\(t'\) 的尾指標，滿足 \(|t_h|=k-j\)，\(S_3\) 的頭指標
• \(S_3\)：未掃描的串

演演算法流程

考慮每次將 \(k\) 右移一位，並且討論 \(S_j\) 和 \(S_k\) 的大小關係

• \(S_j=S_k\)，\(t'\) 與 \(t_h\) 繼續匹配即可 \(j\gets j+1,k\gets k+1\)
• \(S_j<S_k\)，此時根據引理可以知道新的 \(t'\) 會變成一個 LW 滿足 \(t'>t_h\)，那麼根據「Lyndon Word 的複合」一節中的結論，\(t_ht'\) 也是一個 LW，那麼由於 \(t_ht'>t_h=t_{h-1}\) 繼續重複不斷使用該結論即可證明 \(t_1t_2\cdots t_ht'\) 為 LW，因此設整個 \(t_1t_2\cdots t_ht'\) 為新的 \(t_1\)，即 \(j\gets i,k\gets k+1\)
• \(S_j>S_k\)，失配了，此時把 \(t_1\sim t_h\) 變成 \(w_{g+1}\sim w_{g+h}\)，後面新生成的 Lyndon 串也不會超過 \(w_{g+h}=t_h\)，並且此時重新匹配 \(k\)，記 \(S_t\) 為 \(t'\) 的第一個字元，即 \(i\gets t,j\gets t,k\gets i+1\)

複雜度分析

注意到只有 \(k\) 會回退，而 \(i\) 每次都是增加的且每次回退 \(k\) 事實上也不減小 \(i+k\) 的值，均攤分析可以證明 Duval 演演算法的複雜度是 \(\Theta(|S|)\) 的

程式碼實現

根據上面的流程，我們能夠寫出如下虛擬碼（記 \(n=|S|\)）：

i=1
while i<=n:
	j=i,k=i+1
	while k<=n and S[j]<=S[k]:
		if S[j]=S[k]:
			j=j+1,k+k+1
		else:
			j=i,k=k+1
	while i<=j:
		print(S[i...(i+k-j+1)])
		i=i+k-j

IV. Lyndon 分解與最小表示

最小表示定義為一個字串 \(S\) 的所有迴圈同構串（含自身）中字典序最小的一個

我們有如下的結論：對 \(S^2\) 進行 Lyndon 分解，設 \(w_i\) 對應子串 \(S^2[l_i\cdots r_i]\)，那麼找到滿足 \(l_i\le |S|< r_i\) 的 \(i\) 則 \(S^2[l_i\cdots l_i+n-1]\) 即為 \(S\) 的最小表示，證明如下：

證：

對於任意迴圈同構串 \(S^2[l\cdots r]\ne S^2[l_i\cdots l_i+n-1]\)，由於 \(|S^2[l\cdots r]|=r-l+1=S\)，那麼 \(r\le |S|\le r_i\) 總是成立，假設 \(S^2[l\cdots r]=w'_jw_{j+1}\cdots\)，其中 \(w'_j\) 為 \(w_j\) 的一個字尾，且我們知道 \(i\le j\)，那麼我們有 \(w'_j>w_j>w_{j+1}>\cdots >w_i\)，這就證明了 \(S^2[l\cdots r]<S[l_i\cdots l_i+n-1]\)

V. 習題演練

[洛谷6114] - 【模板】Lyndon 分解

Problem Link

模板題，直接用 Duval 演演算法求 Lyndon 分解即可

時間複雜度 \(\Theta(|s|)\)

#include<bits/stdc++.h>
using namespace std;
const int MAXN=5e6+5;
char s[MAXN];
signed main() {
	scanf("%s",s+1);
	int n=strlen(s+1),ans=0;
	for(int i=1;i<=n;) {
		int j=i,k=i+1;
		while(k<=n&&s[j]<=s[k]) j=(s[j]==s[k])?(j+1):i,++k;
		while(i<=j) ans^=(i+k-j-1),i+=k-j;
	}
	printf("%d\n",ans);
	return 0;
}

[洛谷1368] - 【模板】最小表示法

Problem Link

模板題，根據我們上面的分析，先用 Duval 演演算法求出 \(\{a_i\}^2\) 的 Lyndon 分解，然後找到滿足條件的 \(w_i\) 即可

時間複雜度 \(\Theta(n)\)

#include<bits/stdc++.h>
using namespace std;
struct node {
	int l,r;
	node() { l=r=0; }
	node(int _l,int _r) { l=_l,r=_r; }
};
const int MAXN=1e6+1;
int S[MAXN];
signed main() {
	vector <node> w;
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;++i) scanf("%d",&S[i]),S[i+n]=S[i];
	int m=n<<1;
	for(int i=1;i<=m;) {
		int j=i,k=i+1;
		while(k<=m&&S[j]<=S[k]) j=(S[j]==S[k])?(j+1):i,++k;
		while(i<=j) w.push_back(node(i,i+(k-j)-1)),i+=k-j;
	}
	for(auto x:w) {
		if(x.l<=n&&n<x.r) {
			for(int i=x.l;i<x.l+n;++i) printf("%d ",S[i]);
			puts(""); break;
		}
	}
	return 0;
}