圖解 Andrew 演演算法求凸包
前言
Andrew 演演算法可以在 \(O(n\log n)\) 的時間複雜度通過單調棧分別求出散點的上凸殼和下凸殼,來求出平面上一些點的凸包。
看懂這篇部落格,大家需要掌握:
- 基礎計算幾何知識
- 單調棧
凸包
首先,什麼是凸包?
給你平面上的點集,你需要從中選出最少的點,使得這些點所組成的 凸多邊形 可以包裹住其他所有點。這些點所組成的凸多邊形就是凸包。
譬如下面這個點集:

它的凸包是:
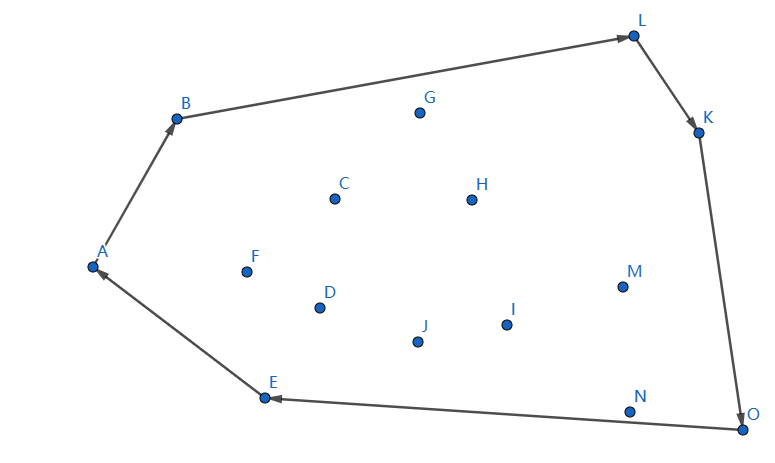
下面我將會告訴大家怎麼求。
序曲
Andrew 演演算法需要先對所有點按照 \(x\) 座標為第一關鍵字、\(y\) 座標為第二關鍵字排序。如上面的點集,經過排序後是:
ABFEDCGJHILMNKO
那麼 \(A\) 和 \(O\) 一定在凸包上,因為它們無法被其他點所組成的凸多邊形覆蓋。
按照 Andrew 演演算法的邏輯,我們需要先求出凸包的一半 「凸殼」。下面將會以上凸殼為例,下凸殼與其類似。
一段上凸殼一定滿足順時針遍歷時,每個節點在每條邊所組成的向量的右邊(下凸殼在左邊)(就是凸包的「凸」,下同)。這句話大家可能不能完全理解,不過沒有關係,我會給大家慢慢道來。
流程
首先,按照排序後的點集遍歷點集,第一個遍歷到的是 \(B\)(\(A\) 不考慮)。我們可以連線 \(AB\):

然後下一個點是 \(F\),繼續連線 \(BF\):
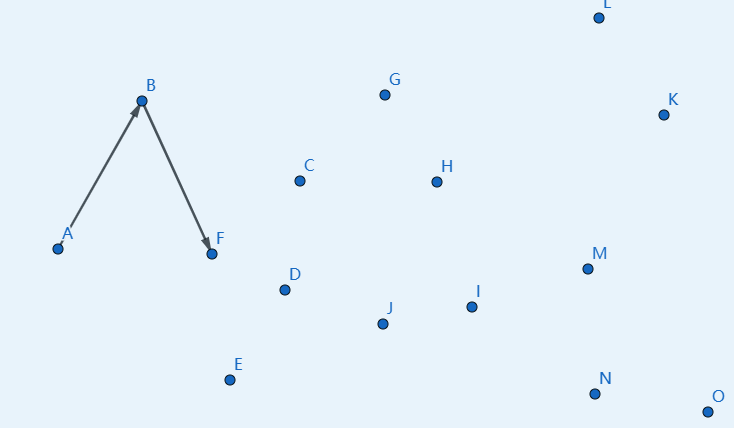
下一個點是 \(E\),繼續連線 \(FE\):
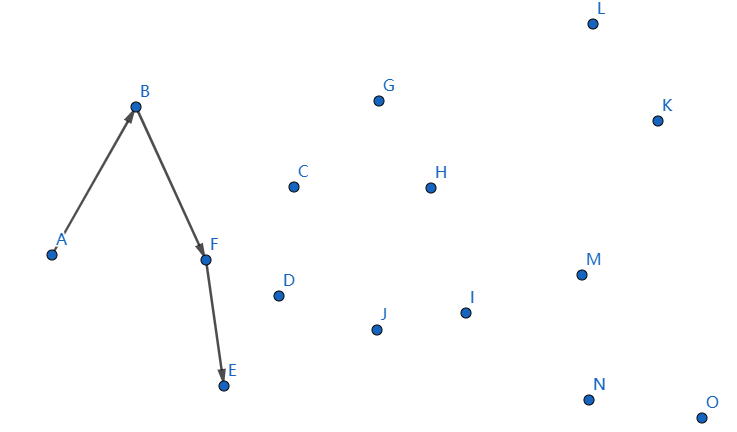
下一個點是 \(D\),繼續連線 \(ED\):
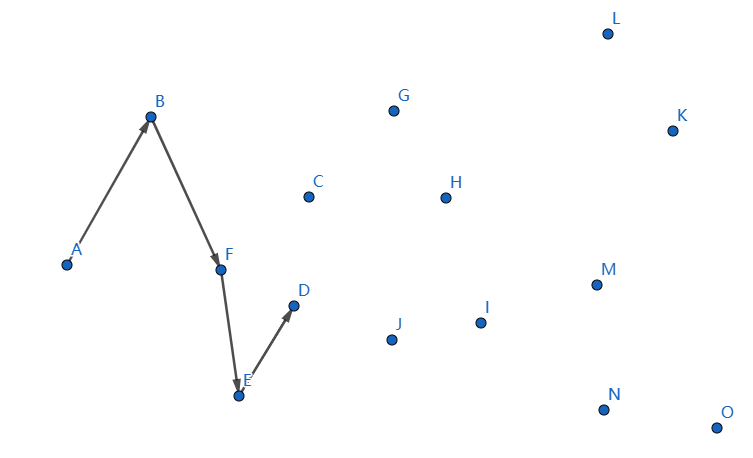
但是這樣子我們遇到了問題,\(D\) 在 \(FE\) 左側,它不凸了,我們的解決辦法是:
斷掉以前連的邊,直到遇到可以連線的點,滿足凸殼性質
我們可以斷掉 \(ED,FE\),連線 \(FD\),發現還是不滿足。
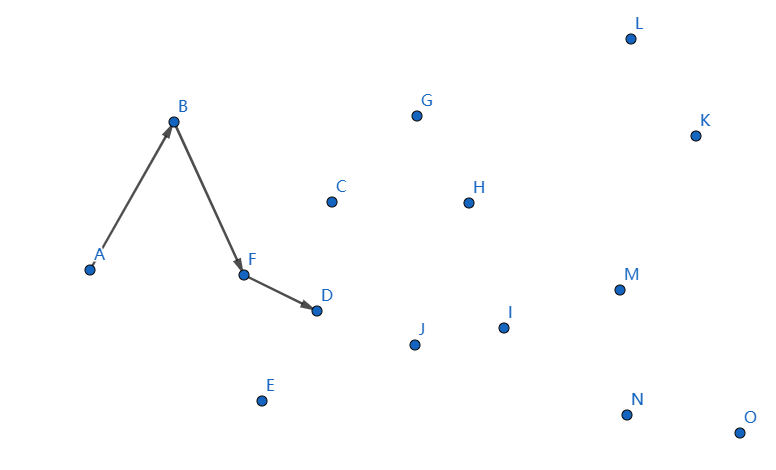
我們繼續,斷掉 \(FD,BF\),連線 \(BD\),這回滿足了。
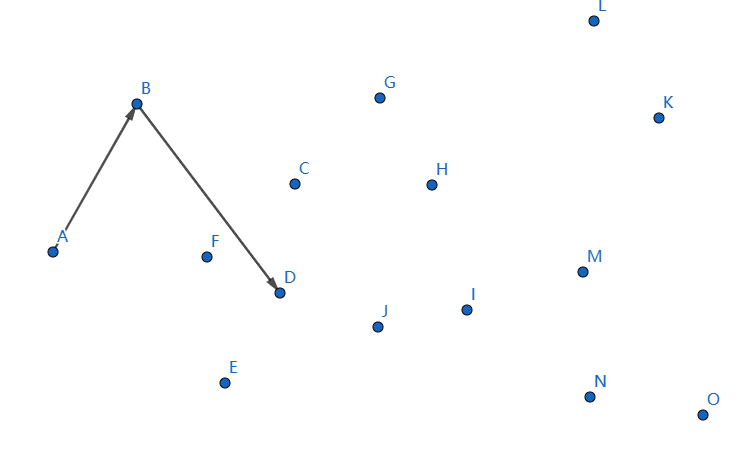
下一個點是 \(C\),繼續連線 \(DC\):
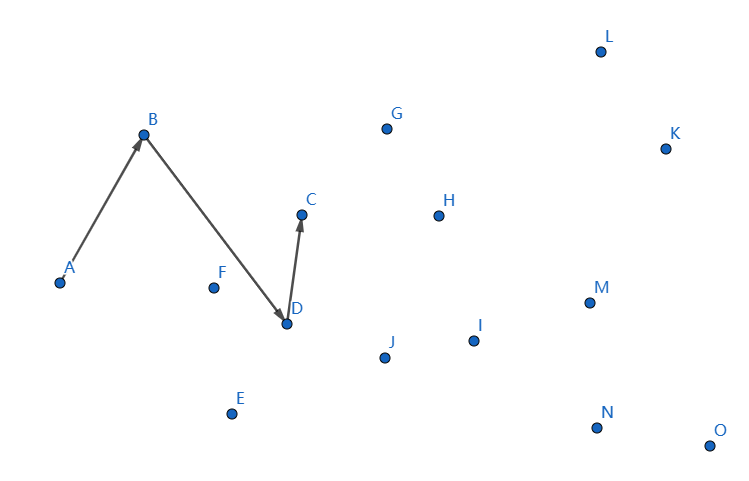
發現又不凸了,我們斷掉 \(DC,BD\) 連線 \(BC\),就可以滿足了:
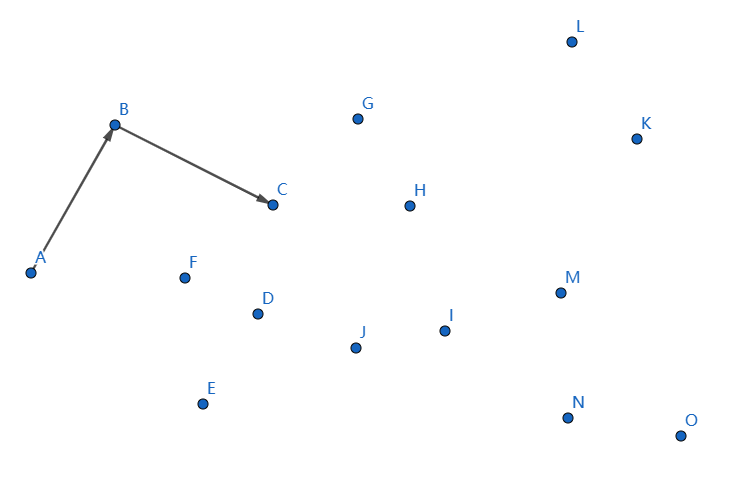
下一個點是 \(G\),繼續連線 \(CG\):
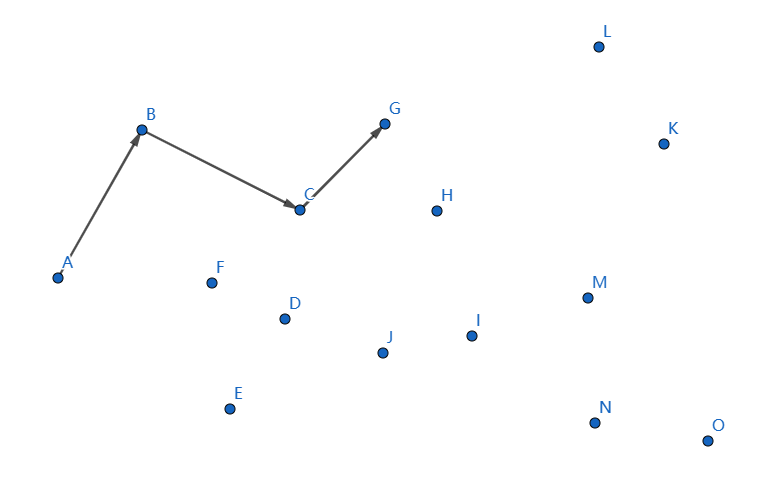
發現不凸,我們斷掉 \(CG,BC\),連線 \(BG\):
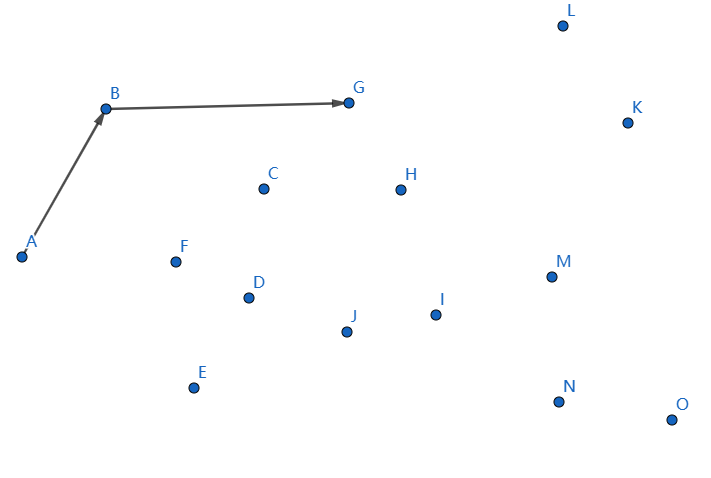
下一個點是 \(J\),繼續連線 \(GJ\):
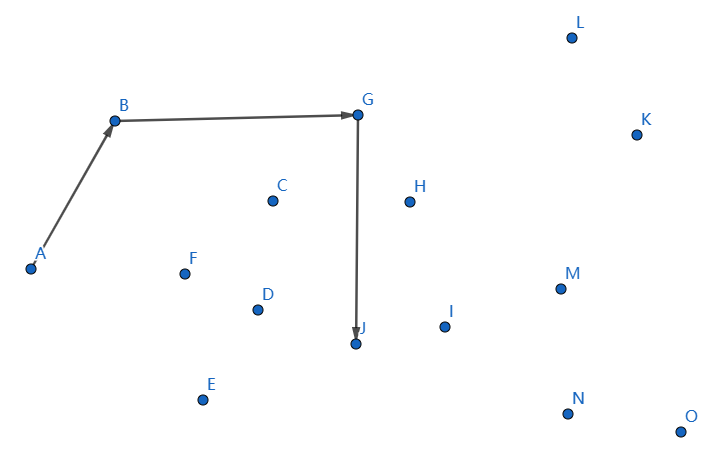
下一個點是 \(H\),繼續連線 \(JH\):
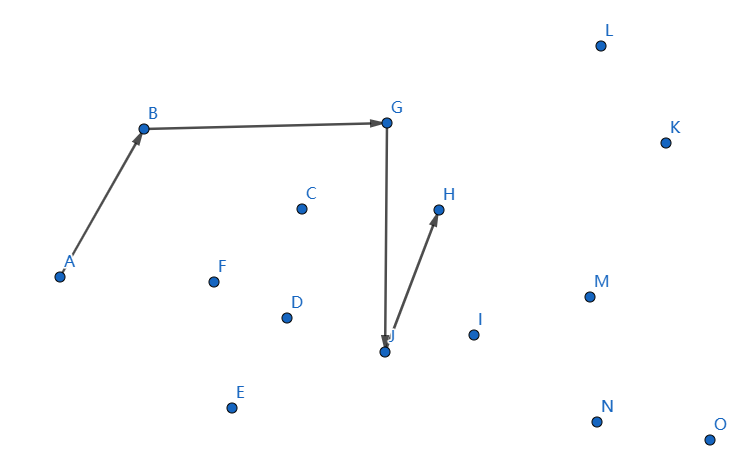
發現不凸,我們斷掉 \(GJ,JH\),連線 \(GH\):
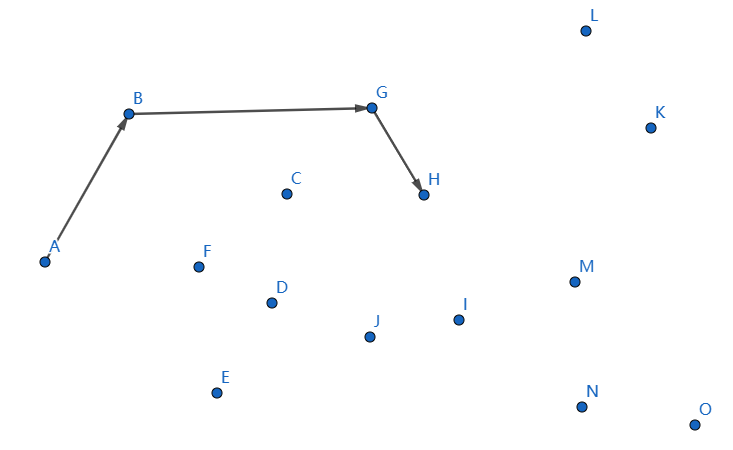
下一個點是 \(I\),繼續連線 \(HI\):
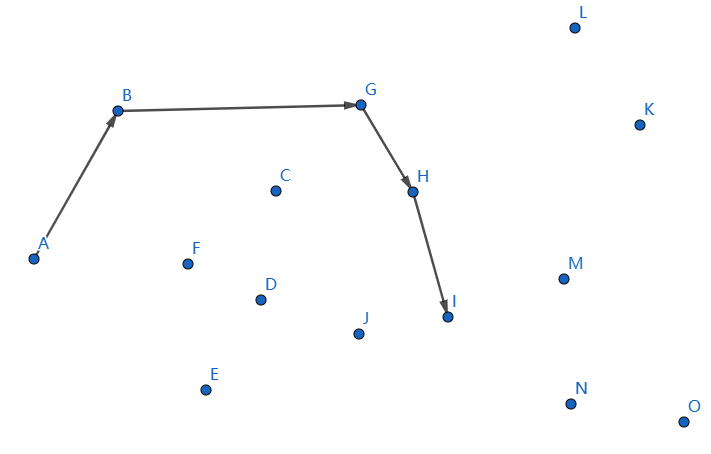
下一個點是 \(L\),繼續連線 \(IL\):
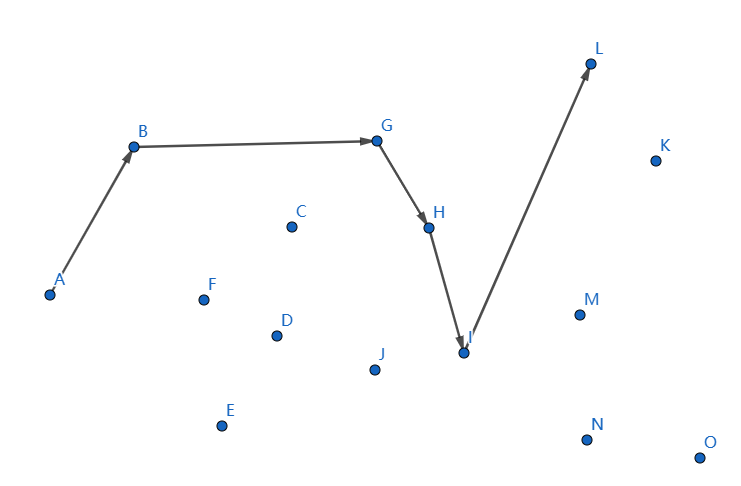
發現不凸,我們斷掉 \(IL,HI\),連線 \(HL\):
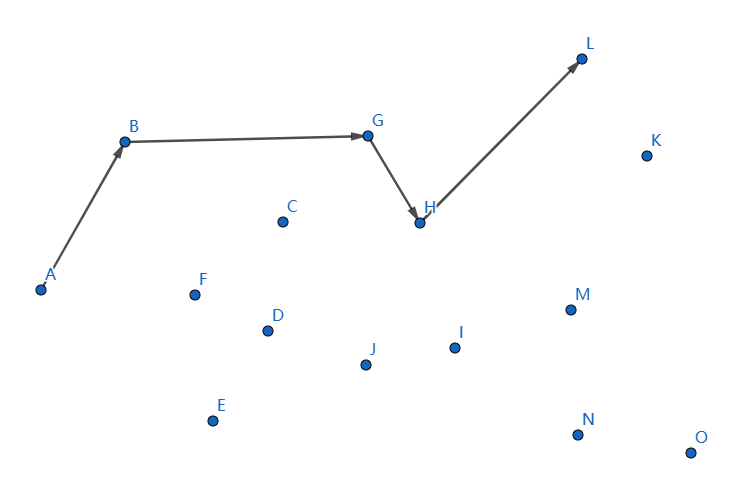
發現不凸,我們斷掉 \(HL,GH\),連線 \(GL\):
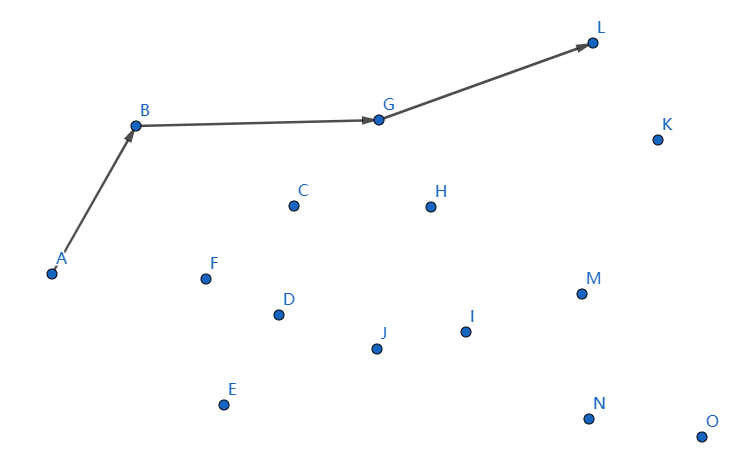
發現不凸,我們斷掉 \(GL,BG\),連線 \(BL\):
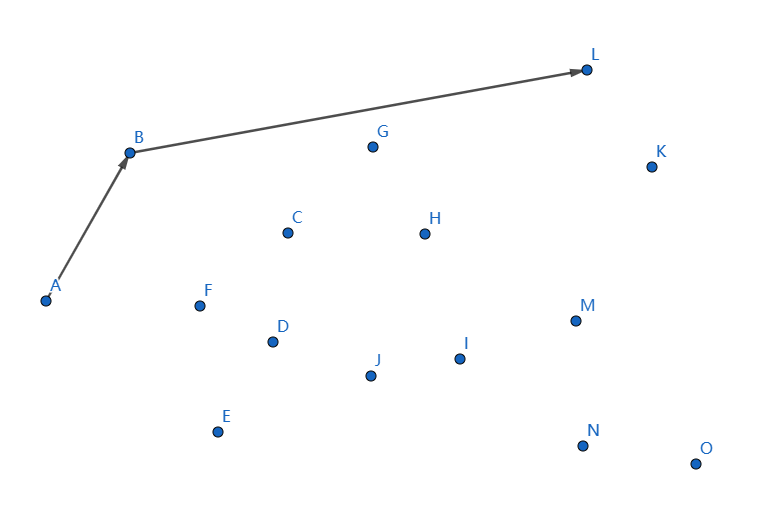
下一個點是 \(M\),繼續連線 \(LM\):
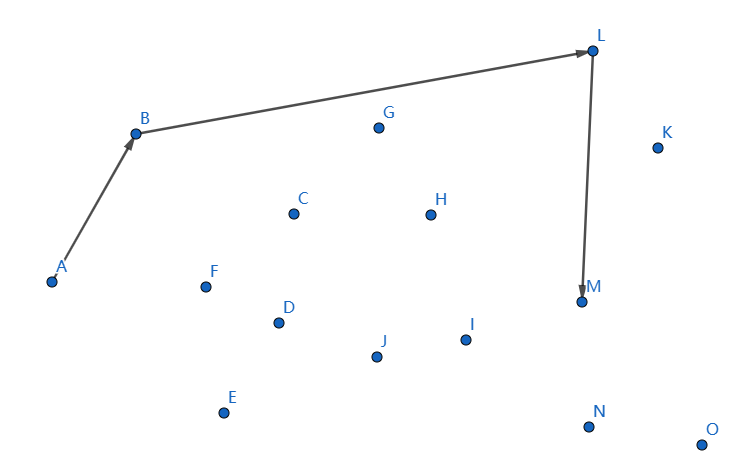
下一個點是 \(N\),繼續連線 \(MN\):
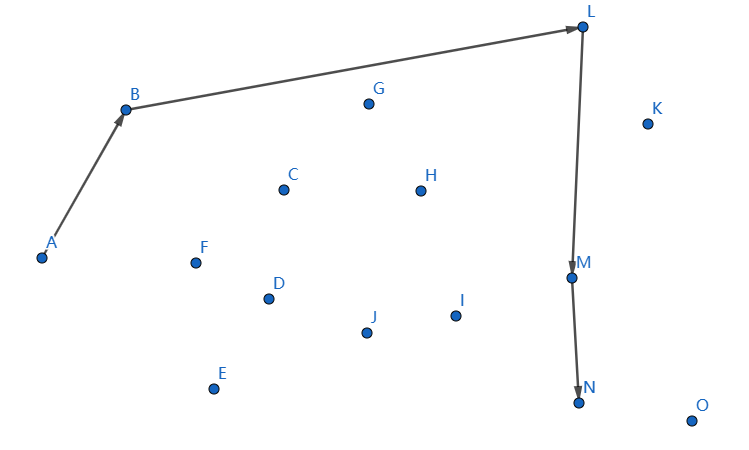
發現不凸,我們斷掉 \(MN,LM\),連線 \(LN\):
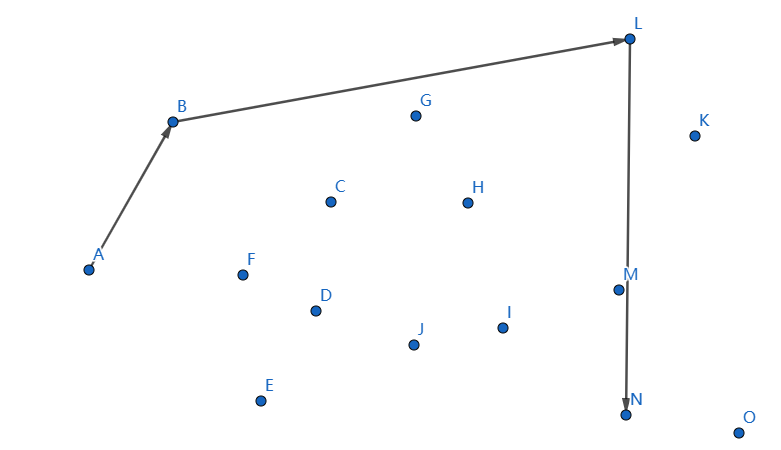
下一個點是 \(K\),繼續連線 \(NK\):
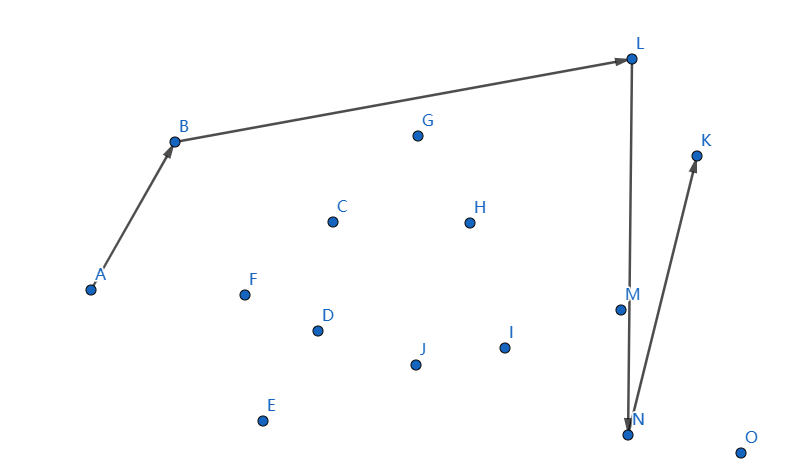
發現不凸,我們斷掉 \(LN,NK\),連線 \(LK\):
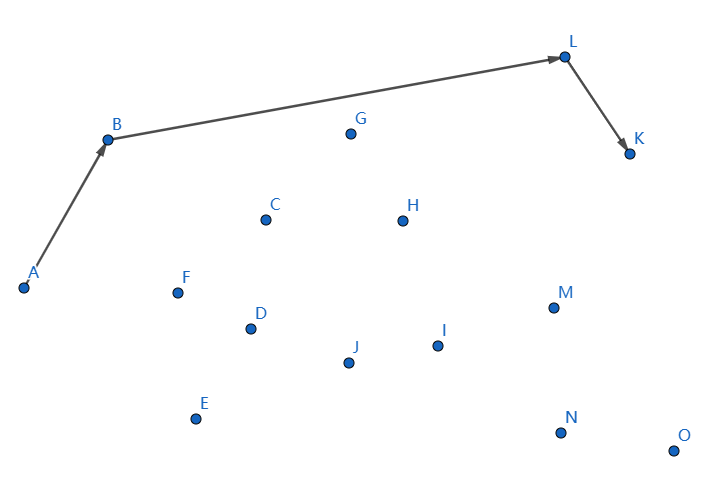
最後一個點是 \(O\),我們連線 \(KO\):
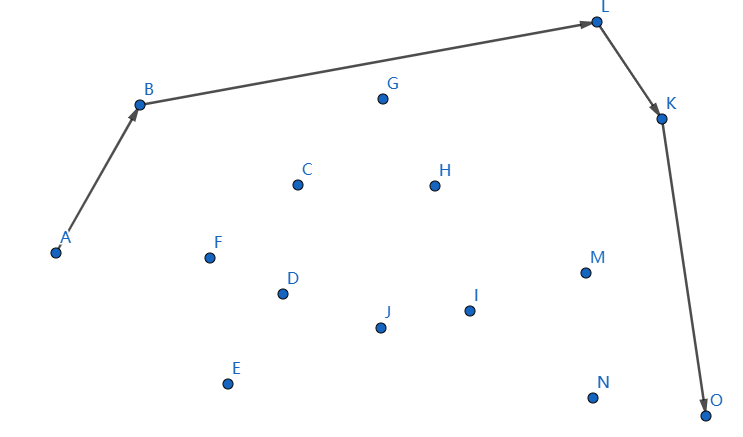
這樣子上凸殼便求出來,下凸殼我們一般從 \(O\) 遍歷到 \(A\),按照以前的邏輯做即可,最後結果如下:
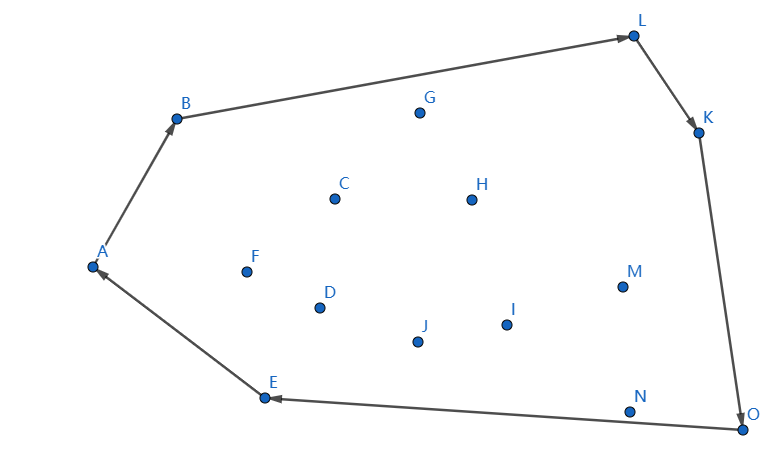
實現
維護「不凸就斷邊」我們使用單調棧,如果不滿足凸的性質就彈棧,最後入棧即可。注意我們不需要模擬斷邊操作,只需要將點刪除即可。
還有,如何判斷是否在左邊呢?我們可以使用叉乘的右手定則:
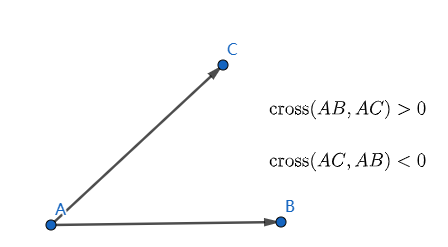
參考程式碼如下:
int stk[100005];
bool used[100005];
vector<Point> ConvexHull(Point* poly, int n){ // Andrew演演算法求凸包
int top=0;
sort(poly+1,poly+n+1,[&](Point x,Point y){
return (x.x==y.x)?(x.y<y.y):(x.x<y.x);
});
stk[++top]=1;
for(int i=2;i<=n;i++){
while(top>1&&dcmp((poly[stk[top]]-poly[stk[top-1]])*(poly[i]-poly[stk[top]]))<=0){
used[stk[top--]]=0;
}
used[i]=1;
stk[++top]=i;
}
int tmp=top;
for(int i=n-1;i;i--){
if(used[i]) continue;
while(top>tmp&&dcmp((poly[stk[top]]-poly[stk[top-1]])*(poly[i]-poly[stk[top]]))<=0){
used[stk[top--]]=0;
}
used[i]=1;
stk[++top]=i;
}
vector<Point> a;
for(int i=1;i<=top;i++){
a.push_back(poly[stk[i]]);
}
return a;
}