論文資訊

論文標題：Joint domain alignment and discriminative feature learning for unsupervised deep domain adaptation
論文作者：Chao Chen , Zhihong Chen , Boyuan Jiang , Xinyu Jin
論文來源：AAAI 2019
論文地址：download 
論文程式碼：download
參照次數：175

1 Introduction

　　近年來，大多數工作集中於減少不同領域之間的分佈差異來學習共用的特徵表示，由於所有的域對齊方法只能減少而不能消除域偏移，因此分佈在簇邊緣或遠離相應類中心的目標域樣本很容易被從源域學習到的超平面誤分類。為緩解這一問題，提出聯合域對齊和判別特徵學習，有利於 域對齊 和 分類。具體提出了一種基於範例的判別特徵學習方法和一種基於中心的判別特徵學習方法，兩者均保證了域不變特徵具有更好的類內緊湊性和類間可分性。大量的實驗表明，在共用特徵空間中學習鑑別特徵可以顯著提高效能。
　　域適應，關注如何從源域的大量標記樣本和目標域有限或沒有標記的目標樣本學習分類，可以分為如下三種方法：

• • feature-based domain adaptation
  • instance-based domain adaptation
  • classifier-based domain adaptation

2 Method

　　總體框架如下：

　　　　

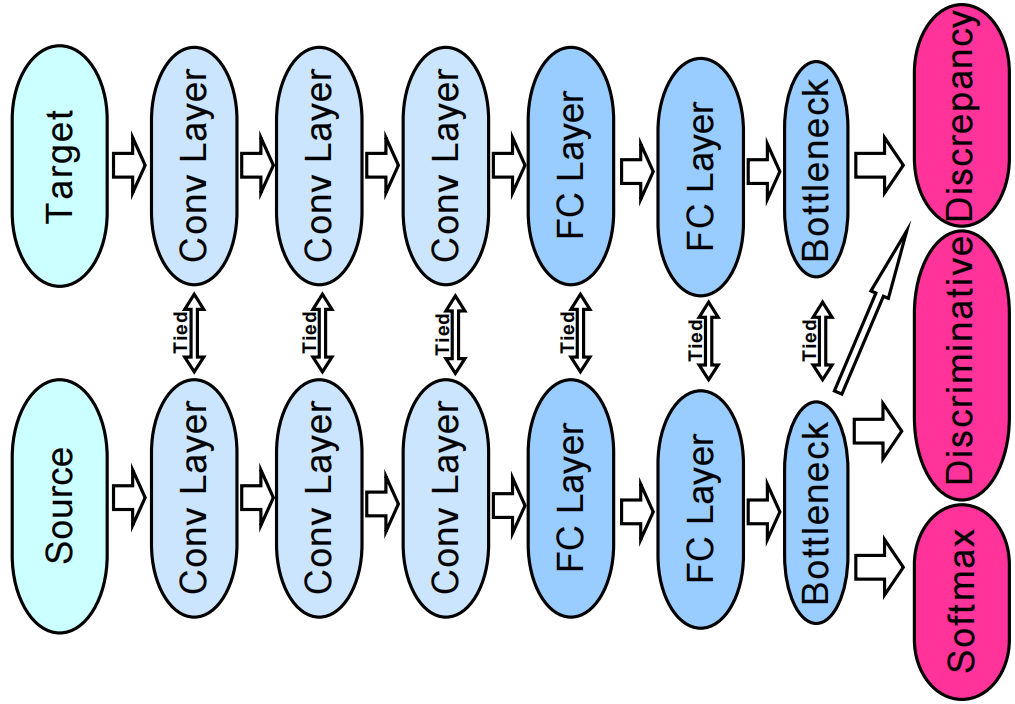
2.1 Problem statement

　　In this work, following the settings of unsupervised domain adaptation, we define the labeled source data as  $\mathcal{D}^{s}=  \left\{\mathbf{X}^{s}, \mathbf{Y}^{s}\right\}=\left\{\left(\boldsymbol{x}_{i}^{s}, y_{i}^{s}\right)\right\}_{i=1}^{n_{s}}$  and define the unlabeled target data as  $\mathcal{D}^{t}=\left\{\mathbf{X}^{t}\right\}=\left\{\boldsymbol{x}_{i}^{t}\right\}_{i=1}^{n_{t}}$ , where  $\mathbf{x}^{s}$  and  $\mathbf{x}^{t}$  have the same dimension  $\mathbf{x}^{s(t)} \in \mathbb{R}^{d}$ . Let  $\boldsymbol{\Theta}$  denotes the shared parameters to be learned.  $\mathbf{H}_{s} \in \mathbb{R}^{b \times L}$  and  $\mathbf{H}_{t} \in \mathbb{R}^{b \times L}$  denote the learned deep features in the bottleneck layer regard to the source stream and target stream, respectively.  $b$  indicates the batch size during the training stage and  $L$  is the number of hidden neurons in the bottleneck layer. Then, the networks can be trained by minimizing the following loss function.

　　　　$\begin{array}{l}\mathcal{L}\left(\boldsymbol{\Theta} \mid \mathbf{X}_{s}, \mathbf{Y}_{s}, \mathbf{X}_{t}\right)=\mathcal{L}_{s}+\lambda_{1} \mathcal{L}_{c}+\lambda_{2} \mathcal{L}_{d}    \quad\quad(1)\\\mathcal{L}_{s}=\frac{1}{n_{s}} \sum_{i=1}^{n_{s}} c\left(\boldsymbol{\Theta} \mid \boldsymbol{x}_{i}^{s}, y_{i}^{s}\right)  \quad\quad \quad\quad \quad\quad\quad\quad(2)\\\mathcal{L}_{c}=C O R A L\left(\mathbf{H}_{s}, \mathbf{H}_{t}\right)  \quad\quad \quad\quad \quad\quad \quad\quad(3)\\\mathcal{L}_{d}=\mathcal{J}_{d}\left(\boldsymbol{\Theta} \mid \mathbf{X}^{s}, \mathbf{Y}^{s}\right)  \quad\quad \quad\quad \quad\quad\quad\quad \quad\quad(4)\end{array}$

　　其中

• • $\mathcal{L}_{s}$ 代表源域分類損失；
  • $\mathcal{L}_{c}=\operatorname{CORAL}\left(\mathbf{H}_{s}, \mathbf{H}_{t}\right) $ 表示通過相關性對齊度量的域差異損失；
  • $\mathcal{J}_{d}\left(\boldsymbol{\Theta} \mid \mathbf{X}^{s}, \mathbf{Y}^{s}\right) $ 代表鑑別損失，保證了域不變特徵具有更好的類內緊緻性和類間可分性；

2.2 Correlation Alignment ($\text{CORAL}$)

　　為學習域不變特徵，通過對齊源特徵和目標特徵的協方差來減少域差異。域差異損失如下：

　　　　$\mathcal{L}_{c}=\operatorname{CORAL}\left(\mathbf{H}_{s}, \mathbf{H}_{t}\right)=\frac{1}{4 L^{2}}\left\|\operatorname{Cov}\left(\mathbf{H}_{s}\right)-\operatorname{Cov}\left(\mathbf{H}_{t}\right)\right\|_{F}^{2}\quad\quad(5)$

　　其中：

• • $\|\cdot\|_{F}^{2}$ 為矩陣 $\text{Frobenius}$ 範數；　　
  • $\operatorname{Cov}\left(\mathbf{H}_{s}\right)$ 和 $\operatorname{Cov}\left(\mathbf{H}_{t}\right)$ 表示 $\text{bottleneck layer}$ 中源特徵和目標特徵的協方差矩陣；　　
    • $\operatorname{Cov}\left(\mathbf{H}_{s}\right)=\mathbf{H}_{s}^{\top} \mathbf{J}_{b} \mathbf{H}_{s}$
    • $\operatorname{Cov}\left(\mathbf{H}_{t}\right)=\mathbf{H}_{t}^{\top} \mathbf{J}_{b} \mathbf{H}_{t}$
      • $\mathbf{J}_{b}=\mathbf{I}_{b}-\frac{1}{b} \mathbf{1}_{n} \mathbf{1}_{n}^{T^{s}}$ 是 $\text{centralized matrix}$；
      • $\mathbf{1}_{b} \in \mathbb{R}^{b}$ 全 $1$ 列向量；
      • $b$ 是批大小；

　　注意，訓練過程是通過小批次 $\text{SGD}$ 實現的，因此，在每次迭代中，只有一批訓練樣本被對齊。

2.3 Discriminative Feature Learning

　　為學習更具判別性的特徵，提出兩種判別特徵學習方法：基於範例的判別特徵學習 和 基於中心的判別特徵學習。

　　注意，整個訓練階段都是基於小批次 $\text{SGD}$ 的。因此，下面給出的鑑別損失是基於一批樣本的。

2.3.1 Instance-Based Discriminative Loss

　　基於範例的判別損失 $\mathcal{L}_{d}^{I}$ 可以表示為：

　　其中：

• • $\mathbf{H}_{s}=\left[\mathbf{h}_{1}^{s} ; \mathbf{h}_{2}^{s} ; \cdots ; \mathbf{h}_{b}^{s}\right] $；
  • $C_{i j}=1$ 表示 $\mathbf{h}_{i}^{s}$ 和 $\mathbf{h}_{j}^{s}$ 來自同一個類，$C_{i j}=0$ 表示 $\mathbf{h}_{i}^{s}$ 和 $\mathbf{h}_{j}^{s}$ 來自不同的類；
  • $m_{2}$ 大於 $m_{1}$；

　　從 $\text{Eq.6}$、$\text{Eq.7}$ 中可以看出，判別損失會使類內樣本之間的距離不超過 $m_{1}$，而類間樣本之間的距離至少 $m_{2}$。

　　　　$\begin{aligned}\mathcal{L}_{d}^{I} =\alpha\left\|\max \left(0, \mathbf{D}^{H}-m_{1}\right)^{2} \circ \mathbf{L}\right\|_{\text {sum }}+\left\|\max \left(0, m_{2}-\mathbf{D}^{H}\right)^{2} \circ(1-\mathbf{L})\right\|_{s u m}\end{aligned}\quad\quad(8)$

　　　　$\begin{array}{c}\mathcal{L}_{d}^{C}=\beta \sum\limits _{i=1}^{n_{s}} \max \left(0,\left\|\mathbf{h}_{i}^{s}-\mathbf{c}_{y_{i}}\right\|_{2}^{2}-m_{1}\right)+\sum\limits_{i, j=1, i \neq j}^{c} \max \left(0, m_{2}-\left\|\mathbf{c}_{i}-\mathbf{c}_{j}\right\|_{2}^{2}\right)\end{array}\quad\quad(9)$

　　其中：

• • $\beta$ 為權衡引數；
  • $m_{1}$ 和 $m_{2}$ 為兩個約束邊距 $\left(m_{1}<m_{2}\right)$；
  • $\mathbf{c}_{y_{i}} \in \mathbb{R}^{d}$ 表示第 $y_{i}$ 類的質心，$y_{i} \in\{1,2, \cdots, c\}$，$c$ 表示類數；　　

　　理想情況下，類中心 $\mathbf{c}_{i}$ 應通過平均所有樣本的深層特徵來計算。但由於本文是基於小批次進行更新的，因此很難用整個訓練集對深度特徵進行平均。在此，本文做了一個必要的修改，對於 $\text{Eq.9}$ 中判別損失的第二項，用於度量類間可分性的 $\mathbf{c}_{i}$ 和 $\mathbf{c}_{j}$ 是通過對當前一批深度特徵進行平均來近似計算的，稱之為 「批類中心」 。相反，用於測量類內緊緻性的 $\mathbf{c}_{y_{i}}$ 應該更準確，也更接近 「全域性類中心」。因此，在每次迭代中更新 $\mathbf{c}_{y_{i}}$ 為

　　　　$\begin{array}{l}\Delta \mathbf{c}_{j}=\frac{\sum\limits _{i=1}^{b} \delta\left(y_{i}=j\right)\left(\mathbf{c}_{j}-\mathbf{h}_{i}^{s}\right)}{1+\sum\limits_{i=1}^{b} \delta\left(y_{i}=j\right)} \quad\quad(10) \\\mathbf{c}_{j}^{t+1}=\mathbf{c}_{j}^{t}-\gamma \cdot \Delta \mathbf{c}_{j}^{t}\quad\quad(11)\end{array}$

　　「全域性類中心」 在第一次迭代中被初始化為「批類中心」，在每次迭代中通過 $\text{Eq.10}$、$\text{Eq.11}$ 進行更新，其中 $\gamma$ 是更新「全域性類中心」的學習速率。為簡潔起見，$\text{Eq.9}$ 可以簡化為

　　　　$\begin{array}{r}\mathcal{L}_{d}^{C}=\beta\left\|\max \left(0, \mathbf{H}^{c}-m_{1}\right)\right\|_{\text {sum }}+ \left\|\max \left(0, m_{2}-\mathbf{D}^{c}\right) \circ \mathbf{M}\right\|_{\text {sum }}\end{array}$

　　其中：

• • $\mathbf{H}^{c}=\left[\mathbf{h}_{1}^{c} ; \mathbf{h}_{2}^{c} ; \ldots ; \mathbf{h}_{b}^{c}\right]$，$\mathbf{h}_{i}^{c}=\left\|\mathbf{h}_{i}^{s}-\mathbf{c}_{y_{i}}\right\|_{2}^{2}$ 表示第 $i$ 個樣本深層特徵與其對應的中心 $\mathbf{c}_{y_{i}}$ 之間的距離；
  • $  \mathbf{D}^{c} \in \mathbb{R}^{c \times c} $ 表示「批類中心」的成對距離，即 $\mathbf{D}_{i j}^{c}=\left\|\mathbf{c}_{i}-\mathbf{c}_{j}\right\|_{2}^{2} $；

　　不同於 $\text{Center Loss }$，它只考慮類內的緊緻性，本文不僅懲罰了深度特徵與其相應的類中心之間的距離，而且在不同類別的中心之間加強了較大的邊際。

2.4 Training

　　所提出的 $\text{Instance-Based joint discriminative domain adaptation (JDDA-I)}$和 $\text{Center-Based joint discriminative domain adaptation (JDDA-C)}$ 都可以通過小批次SGD輕鬆實現。對於 $\text{JDDA-I}$，總損失為  $\mathcal{L}=\mathcal{L}_{s}+\lambda_{1} \mathcal{L}_{c}+\lambda_{2}^{I} \mathcal{L}_{d}^{I}$，$\mathcal{L}_{c}$ 代表源域的分類損失。因此，引數 $\Theta$ 可以通過標準的反向傳播直接更新

　　　　$\Theta^{t+1}=\Theta^{t}-\eta \frac{\partial\left(\mathcal{L}_{s}+\lambda_{1} \mathcal{L}_{c}+\lambda_{2}^{I} \mathcal{L}_{d}^{I}\right)}{\partial \mathbf{x}_{\mathbf{i}}}\quad\quad(13)$ 

 

 

====